雷电电磁场空间分布模型
赵玉龙,刘光斌,余志勇,黄 伟
(1.解放军第二炮兵工程大学,陕西 西安 710025;2.解放军71217部队司令部,山东 莱阳 265200)
0 引言
雷电(Lightning,也被称为闪电)指带电云层内部、云层与云层间或云层与大地间发生的放电现象,它伴随强烈的闪光和巨大响声[1],主要分为云地闪和云闪两种。但由于雷电的发生随机性较大,危险系数极高,直接运用于试验研究难度较大。因此,学术界相继提出了雷电放电通道的多种计算模型作为雷电研究的基础,主要包括气动模型(Gas Dynamic Models)、电磁场模型(Electromagnetic Models)、RL-C传输线模型(R-L-C transmission-line models)和工程模型(Engineering Models)[2]。其中,工程模型在国内外的雷电研究工作中应用最为广泛,这主要是因为利用工程模型的建模计算可得到实测的雷电电磁场强度[3],这种研究思路与雷电实际测量工作很接近。
一直以来,人们对于雷电进行了大量的研究,其中,文献[3—4]对雷击点为地面建筑物时,在不考虑地面电导率的条件下,进行了雷电回击电磁场理论研究以及模拟试验研究,对于建筑防雷起到了较好的指导作用;另外,还有学者应用一种新型天线理论,并考虑地面的有限电导率,综合对LEMP进行了研究[5];Rakov、Nuuci等学者就雷电通道的研究开展过一些具有重要意义的工作;Rubinstein应用单极子和偶极子技术求解了雷电电磁场的麦克斯韦方程,但是,单极子技术误差较大[6],不利于得到雷电电磁场的精确解。而对于云闪的研究主要致力于云闪通道形态、放电过程等特征的研究,国外学者进行了重要的研究[7-13];国内也有学者对云闪的发生、发展进行了相关的研究[14],总结出了云闪的一些特征和资料。
总之,国内外大多数的雷电研究局限于地面建筑物、电气设备等地面场点附近的云地闪电,研究已较为成熟,并得到了一些宝贵的资料和数据,研究成果也广泛地应用于这些领域的雷电防护中。但是,随着国防现代化建设的步伐不断加快,国防军事领域飞行器中一些设备信息化程度也越来越高,微电子设备高度集成,越来越精密化、智能化和小型化,应用广泛。因此,本文推导空间任意场点处的雷电电磁场计算表达式。
1 偶极子法求解雷电电磁场
大量的观测事实证明,雷电放电通道极不规则,放电通道形状随意性较大,往往具有倾斜、弯曲、分支和扭曲等。国内外对雷电放电通道建模研究时,将其作简化且等效为垂直于地面的一根导线,按照天线理论进行研究[15],即不考虑通道的分支及放电波形在传播中的变形等因素。雷电对处于其放电通道中的各设备影响,可以通过求解时变电流在空间任意场点引起的电磁场来分析,主要理论分析依据就是应用偶极子理论求解Maxwell方程组。
时变电磁场的Maxwell方程组为:

式 (1)中,ε0为 介 电 常 数 (F/m),μ0为 磁 导 率(H/m),ρ和J分别表示电荷和电流密度,B表示磁通量密度(wb/m2),E表示场强,H 表示磁场强度(A/m),把v1定义为雷电波速度(v1=1/),在空气中等于光速,即为2.998×108m/s。在已知雷电辐射源(dV)的情况下,如图1。一般求解电位φ和矢量磁位A,代替E和H 。

以及考虑到Lorentz条件:

将式(2)、式(3)、式(4)代入式(1),即可得到变换后的Maxwell方程组:

求解式(5),得到非齐次一般解:

解中的r和r'关系如图1所示。

图1 求解示意图Fig.1 Solution sketch map
2 任意空间雷电电磁场分布
在雷电电磁场的理论计算研究中,建立精准的雷电放电通道模型是重中之重,也是雷电研究的基础和前提。如图2所示,将雷电放电回击通道等效为垂直于地面的长为H的竖直天线,其中P(r,φ,z)表示位于雷电电磁场中的空间任意场点,雷电回击电流以速度v匀速沿通道向上传输。h表示t时刻通道回击电流前沿所到达的高度,h上方电流为0。

图2 雷电回击物理模型Fig.2 Physics model of lightning return strike
依照偶极子理论,在通道中选取任一个电荷dz'作为研究对象,电荷距地面高度为z',则-z'处建立一个镜像等效电荷,放电通道附加镜像电流-h,以此建立雷电电磁场计算柱坐标系,如图3所示。
结合图2、图3,应用偶极子原理求解上述Maxwell方程组。求解式(4)得电位φ:

将式(7)代入式(2),即求得E :


图3 电磁场柱坐标系Fig.3 Pole coordinate of electromagnetic field
如图2所示,偶极子dz'电流用i(z',t)描述,az表示Z向单位矢量势,则由式(6)求得矢量磁位A:

再将式(9)代入式(3)、式(8),就得到空间任意一场点P的电场和磁场计算式:


式中,r、z)、φ分别表示径向坐标、轴向坐标、方位角,各分量的含义以及几何关系可参考图3得到,其中R=。不难发现,柱坐标系下雷电场的电场场强分布与φ无关,因此雷电总电场又可定义为:
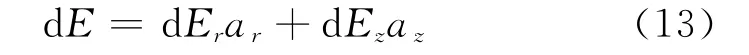
采用相应的雷电流模型,就可以计算空间雷电电磁场的理论值。h可由海维赛德(Heaviside)函数[16]导出,其定义如下:

即令:

即可推导出:

3 雷电电磁场数值仿真
实际雷电电磁场的研究中,地面(z=0)是一特殊的场点,人们的生产、生活都是在地面场点进行的,同样,对于雷电的实际测量工作也是在地面进行的。直接计算空间任意场点电磁场难度较大,因为式(10)、式(11)、式(12)中有大量的积分运算,因此,本章对于地面场点(即z=0)处的雷电电磁场进行数值仿真计算,验证雷电电磁场的理论计算正确性。应用上一章的理论分析和推导公式,分别计算雷电流峰值I0=200kA,云层高度H=7.5km时,地面上场点(z=0)距离分别为r=5km,r=100km处的电场和磁场强度。其中,ε0=8.854×10-12F/m,v取0.5c,(c是真空中的光速,为2.998×108m/s)。仿真结果如图4所示。

图4 地面场点距离r=5km、r=100km处电磁场Fig.4 LEMP on the ground level r=5km 、r=100km
不难发现,云地闪电产生的雷电电磁场,与雷电回击通道的高度、雷电流的大小、场点高度以及场点P与通道间的距离等多个因素有关。其中,雷电流回击速度对雷电电磁场场强影响较大,而对于雷电电磁场磁场强度影响较小。
对于雷电电磁场的场强分布,当h<H时,雷电产生的电场随h的升高而增强,而随着距离r的增大,场强呈逐渐减小的趋势;对于雷电电磁场的磁场强度分布,磁场强度随着高度h的增加和水平距离r的增加,呈逐渐减小的趋势,最终的数值仿真结果和实际的雷电电磁场的变化规律是相吻合的,证明了本文雷电电磁场计算方法的可行性。地面场点电磁场的计算分析,对于地面附近雷电防护研究具有较为重要的指导作用。
4 结论
本文重点推导了空间任意场点处的雷电电磁场计算表达式,该式表明云地闪电产生的雷电电磁场,与雷电流回击速度、雷电回击通道的高度、雷电流大小、场点高度以及场点P与通道间的距离等多个因素有关。对地面场点(即z=0)处的雷电电磁场的数值仿真结果表明:对于雷电电磁场的场强分布,当h<H时,雷电产生的电场随h的升高而增强,而随着距离r的增大,场强呈逐渐减小的趋势;对于雷电电磁场的磁场强度分布,磁场强度随着高度h的增加和水平距离r的增加,呈逐渐减小的趋势。数值仿真结果和实际的雷电电磁场的变化规律是相吻合的,证明了本文雷电电磁场计算方法的可行性,这对于地面附近雷电防护研究具有较为重要的支撑作用。
[1]刘有菊,和伟.雷电放电电磁场及保护[M].第一版.昆明:云南大学出版社,2009.
[2]李韦霖,杨琳,李慧,等.雷电通道模型研究与应用[J].现代电子技术,2010,33(5):174-178.LI Weilin,YANG Lin,LI Hui,et al.Research and application of lightning channel model[J].Modern Electronics Technique,2010,33(5):174-178.
[3]José Luis Bermudez,Farhad Rachidi,Wasyl Janischewskyj,et al.Far-field-current relationship based on the TL model for lightning return strokes to elevated strike objects[J].IEEE Transactions on Electromagnetic Compatibility,2005,47(1):146-157.
[4]Yoshihiro Baba,Vladimir A.Rakov.On the interpretation of ground reflections observed in small-scale experiments simulating lightning strikes to towers[J].IEEE Transactions on Electromagnetic Compatibility,2005,47(3):533-542.
[5]Abdolhamid Shoory,Rouzbeh Moini,S.H.H.Sadeghi.Analysis of Lightning Electromagnetic Fields in the Vicinity of a Lossy Ground Using a New Antenna Theory Model[C]//2003IEEE Bologna PowerTech Conference.us:IEEE,2003:23-26.
[6]Marcos Rubinstein,Uman M A.Transient electric and magnetic fields associated with establishing a finite electrostatic dipole,revisited[J].IEEE Transactions on Electromagnetic Compatibility,1991,33(4):350-359.
[7]Le Vine D M,Menghini R.Electromagnetic fields radiated from a lightning return stroke:Application of an exact solution to Maxwell's equations[J].Journal of Geophysical Research,1978(83):2 377-2 384.
[8]Hager W W,Wang Dongxing.An analysis of errors in the location,current,and velocity of lightning[J].Journal of Geophysical Research,1995,100(D12):25 721-25 729.
[9]Bils J R,Thomson E M,Uman M A,et al.Electric field pulses in close lighting cloud flashes[J].Journal of Geophysical Research,1988,93:15933-15940.
[10]Ogawa T,Brook M.The mechanism of the intracloud lightning discharge[J].Journal of Geophysical Research,1964(69):5 141-5 150.
[11]Liu X S,Krehbiel P R.The initial streamer of intracloud lightning flashes[J].Journal of Geophysical Research,1985(85):4 091-4 095.
[12]Shao X M,Krehbiel P R.The spatial and temporal development of intracloud lightning[J].Journal of Geophysical Research,1996,101(D21):26 641-26 668.
[13]Mansell E R,MacGorman D R,Ziegler C L,et al.Simulated three-dimensional branched lightning in a numerical thunderstorm model[J].Journal of Geophysical Research,2002,107(D9):ACL21-12.
[14]谭涌波,陶善昌,祝宝友,等.雷暴云内闪电双层、分枝结构的数值模拟[J].中国科学:地球科学,2006,36(5):486-496.
[15]Valadimir A Rakov,Martine A Uman.Review and evaluation of lightning return stroke models including some aspects of their application[J].IEEE Transactions on Electromagnetic Compatibility,1998,40(4):403-426.
[16]Podgorski A S,Landt J A.Three dimensional time domain modeling of lightning[J].IEEE Trans Power Del,1987,PWRD-2:931-938.

