基于独立分量分析的运动声源波达方向估计

宁 强，方 向，潘 俊，肖介山，何双承

（1.解放军理工大学工程兵工程学院，江苏 南京 210007；2.解放军76332部队，湖北 广水 432721）

0 引言

在阵列信号的处理中，通过对信号子空间的探测并估计出波达方向（Direction of Arrival，DOA），可以实现对信号子空间跟踪［1－3］。对于DOA估计，常用的方法有波束形成法（Beamforming）和盲信号分离法。波束形成法常被用在基于雷达或声音的定位、卫星通信、超声波和CT图扫描像分析等领域，如文献［4—5］，属于静止信号源的DOA估计；而盲信号分离（Blind source Separation，BSS）方法常用于生物医学方面，如脑电图、脑磁图及核磁共振成像分析等，如文献［6—7］，属于基于图像的运动目标探测。而对于运动声源的DOA估计，波束形成法和盲信号分离法存在不能分辨临近目标、计算量大等问题［8－9］。

针对上述问题，本文提出基于完全正交分解的独立 分 量 分 析 （Complete Orthogonal Decomposition Independent Component Analysis，COD－ICA）的运动声源DOA估计方法。

1 基本原理

1.1 独立分量分析基本原理

独立分量分析的概念最早由Jutten和Herault［10］等人在20世纪80年代早期提出，它在信号分离、冗余消除和降噪方面的优越性已经受到了广泛地关注。其基本原理为：

x［k］＝ ［x1［k］，x2［k］，…，xn［k］］T为n个传感器对源s（t）采样，k为采样时刻。传感器信号可以描述为：

式中，A为混合矩阵，式（1）描述了源信号混合过程。一般要求n≥m（m为源的个数）。v［k］为噪声。

由于混合矩阵A未知，无法从观测信号直接求出源信号，这就需要构造分离矩阵W。x［k］经预处理后得到z［k］，z［k］＝Tx［k］，则

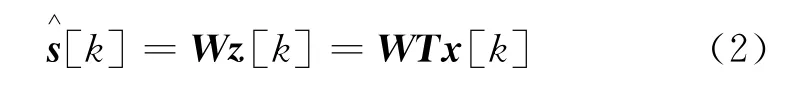
源信号得以分离。

1.2 完全正交分解基本原理

矩阵X［k］（n×N）经GIVENS旋转可作如下分解：

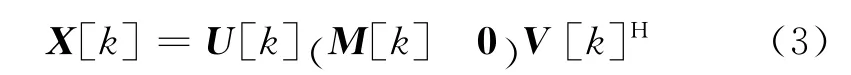
式中，U［k］（n×n）和V［k］（N×N）均为正交矩阵，M［k］为下三角矩阵（或上三角矩阵），如：

式中，L［k］和G［k］均为下三角矩阵，L［k］同时是非异矩阵，这就是矩阵的完全正交分解（COD）［11－12］。

2 运动声源波达方向估计

由于目标声源与环境噪声、测量系统噪声是独立的，固可以采用ICA方法进行DOA估计；又因为目标声源是运动的，其混合系统是时刻变化的，这就要求ICA信号处理系统拥有良好的数据更新能力，所以先采用COD方法对信号进行预处理。

2.1 基于COD的信号预处理

选用COD对采样信号进行预处理，其目的在于：一是便于探测信号子空间，确定信号源数目；二是结合GIVENS旋转便于数据的更新和释放。

如图1所示，将X［k］经COD变换后，由式（4）中L［k］的秩r来确定目标源的个数。当传感器接收到新信号x［k＋1］时，即：［k＋1］＝ ［X［k］，x［k＋1］］，此时经GIVENS旋转，可以得到其COD分解：

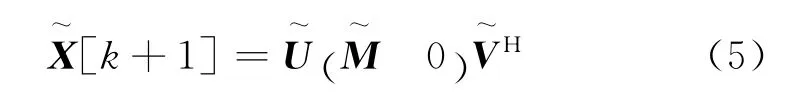
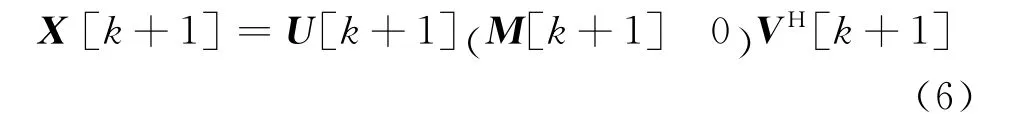
按照上述步骤即完成了信号的更新。

图1 基于COD－ICA的DOA计算流程Fig.1 The flow of DOA based on COD－ICA

2.2 DOA估计

下面对运动声源目标进行DOA估计。

在线白化矩阵T［k＋1］可以表示为：

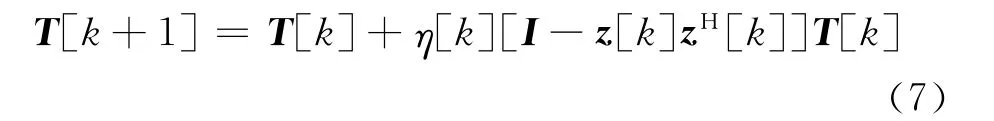
分离矩阵为：W［k＋1］＝W［k］＋η［k］GH［k＋1］。由于（WT）－1与经线性变换和放缩后的混合矩阵A是等价的。则可以由（WT）－1实现DOA估计。

2.3 步长确定

由式（7）可知，要完成DOA估计，还需要确定步长η［k］。

对于时变混合系统，总可以找到足够短的时间窗口η（步长），使得在时间窗口η内声源位置变化比较小，可以认为混合系统变化是不变的，即混合矩阵A是不变的。

此时，步长η的选择至关重要。步长η愈大，计算速度愈快，但计算精度不高；步长η愈小，计算精度愈高，但计算速度慢。因此，计算速度快且精度高的步长η实际上是不存在的，只能在一定精度要求下选择合适的步长。在文献［13—14］中，A.Cichoki提供了多种基于梯度的自适应步长选择方法，并把这些方法统称为步长选择梯度滤波算法。本文采用梯度下降低通滤波进行步长η的确定：

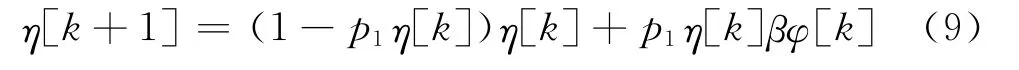
2.4 算法比较

表1给出了以上计算过程的运算量，文献［1］给出了波束形成法的运算量为3mn2＋（mn）2＋O（m3）＋O（nr），可见基于COD－ICA的DOA估计计算更便捷，更易于实现。

表1 COD－ICA运算量Tab.1 Operation count for COD－ICA

3 实验与分析

3.1 实验设置

本次实验采用履带式坦克作为待探测运动目标。考虑到坦克（源信号）之间是相互独立的，同时源信号与噪声（环境噪声和系统噪声）之间也是独立的，满足采用ICA方法进行盲源分离的要求。

坦克从静止启动后，在跑道上匀速直线行驶，由于场地限制坦克速度为20km／h。两个传感器位于坐标点（0.25，－0.25）和（－0.25，0.25），传感器排列方向与坦克行驶方向平行，如图2所示。传感器采样频率为10 240Hz，坦克自带GPS，采样间隔为0.05s，记录其方位角。坦克运动后传感器和GPS开始采样，a、b分别都记录了559 834个采样点，GPS记录了1 200个采样点。

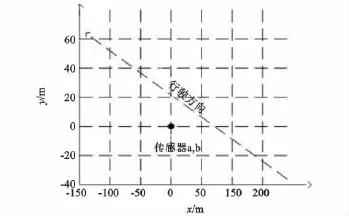
图2 实验示意图Fig.2 The sketch map of experiment

3.2 实验数据分析

图3为a、b两个传感器采集信号的前半部分（2×105个采样点，时长约19.5s）。由于a、b传感器距离比较近（0.7m），可知其信号波形是非常相似的。

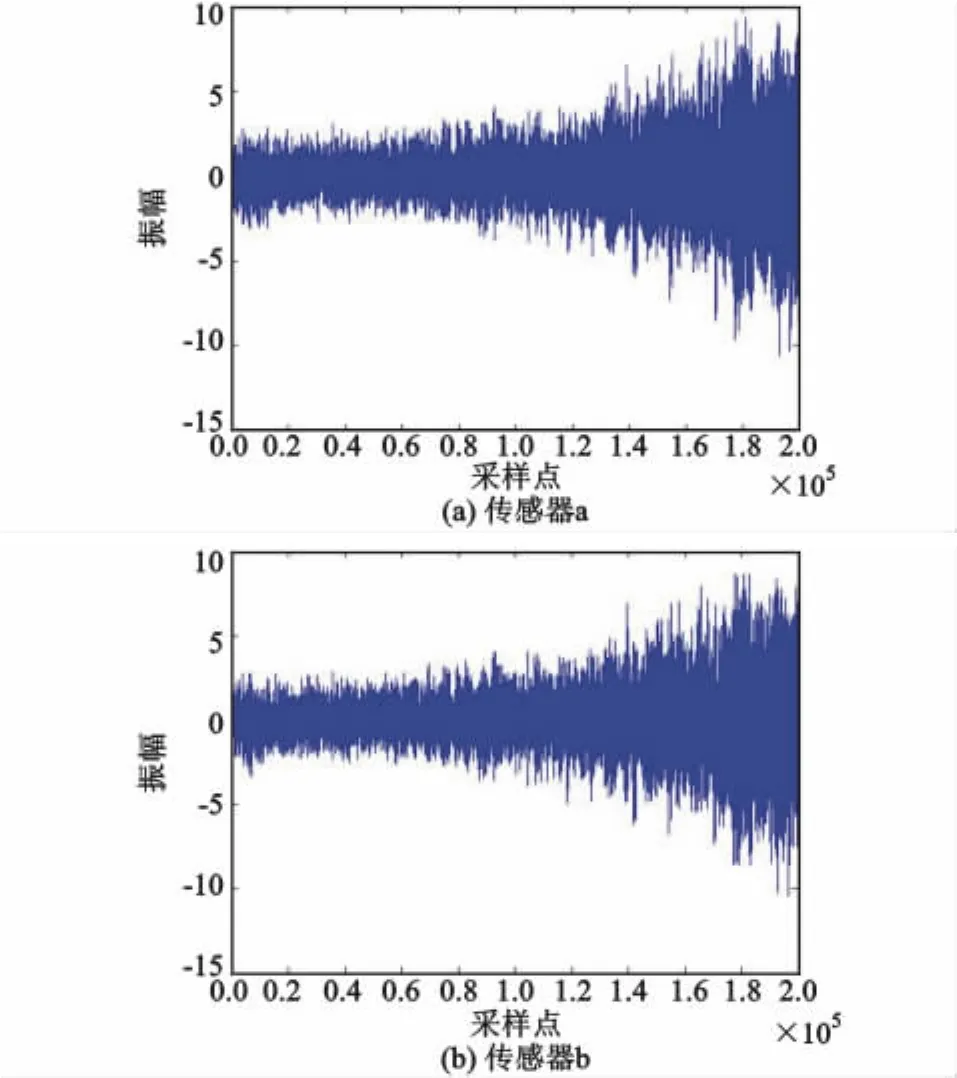
图3 采集信号Fig.3 The collection signal

图4中的横坐标对应GPS采样点。在前40点（即0～2s），采用COD－ICA算法得到的DOA估计与GPS实测值差异比较大；之后DOA估计值迅速收敛；到200点时，DOA估计值与GPS实测值之间的均方差为：MSE＝E｛－α）2｝＝0.035

由图4可以看出，采用COD－ICA算法，并结合梯度下降低通滤波步长选择，能够适时准确实现盲条件下坦克的探测和跟踪。采用梯度下降低通滤波选择步长，能够实现快速收敛。

图4 DOA的计算结果与GPS比较Fig.4 The contrasting between calculation result and GPS data

在坦克驶离传感器较远时，该算法结果与GPS记录数据差异逐渐增大，这是传感器响应信号的信噪比减小的原故。在坦克距离传感器较近时，波达方向变化率增大，此时该算法依然很稳健。

4 结论

本文采用ICA算法对雷场运动声源信号进行DOA估计。通过COD对信号进行去噪和降维预处理，能准确探测声源数量；结合GIVENS旋转实现了ICA算法数据的迅速更新和释放。坦克目标探测试验表明：采用COD－ICA信号处理技术，满足在线数据处理要求，收敛迅速，对运动声源目标波达方向在线估计是可行的，为雷场运动目标的探测和跟踪提供了新的方法。

［1］袁泉，石昭祥.一种基于空间时频分布的波达方向估计方法［J］.探测与控制学报，2007，29（2）：50－53.YUAN Quan，SHI Zhaoxiang.A method of direction－ofarrival via spatial time－frequency distribution［J］.Journal of Detection ＆ Control，2007，29（2）：50－53.

［2］王宏，李洪升，杨日杰，等.一种基于改进传播算子的波达方向估计方法［J］.探测与控制学报，2007，29（3）：41－44.WANG Hong，LI Hongsheng，YANG Rijie，et al.An improved PM－based approach to DOA estimation［J］.Journal of Detection ＆ Control，2007，29（3）：41－44.

［3］金翔，张天骐，侯瑞玲，等.分数阶傅里叶变换与虚拟阵列相结合的波达方向估计［J］.探测与控制学报，2010，32（5）：55－59.JIN Xiang，ZHANG Tianqi，HOU Ruiling，et al.DOA estimation based on combining of fractional fourier transform and virtual array［J］.Journal of Detection ＆ Control，，2010，32（5）：55－59.

［4］Josh Griffith Erling.Ststitical prefomancl analysis of source localization in multisorce，multiarray networks［D］.US：The Pennsylvania State University，2005.

［5］苏永振，袁慎芳.基于独立分量分析的多冲击源定位方法［J］.振动与冲击，2009，28（8）：134－137.SU Yongzhen，YUAN Shenfang.Method for locating multiple impact sources based on independent component analysis［J］.Journal of vibration and shock，2009，28（8）：134－137.

［6］冯毅.基于独立分量分析的运动目标检测与跟踪［D］.大连：大连理工大学，2008.

［7］甘玲，刘国庆.基于小波提升和独立分量分析的运动目标检测［J］.计算机应用于软件，2010，27（5）：257－159.GAN Ling，LIU Guoqing.Moving object based on lifting wavelet transform and independent component analysis［J］.Computer Applications and Software，2010，27（5）：257－159.

［8］Shoko Araki，Hiroshi Sawada，Ryo Mukai，Shoji Makino.DOA estimation for multiple sparse sources with arbitrarily arranged multiple sensors［J］.J sign process syst，2011（63）：265－275.

［9］Masnadi M A，Banani S A.Separation and tracking of maneuvering sources with ICA and particle filters using a new switching dynamic model［J］.IEEE Transactions on aerospace and electronic systems，2010（6）：988－100 5.

［10］Jutten C，Herault J.Blind separation of sources，Part I：An adaptive algorithm based on neuromimatic architecture［J］.Signal Processing，1991，24（1）：1－10.

［11］张贤达.矩阵分析于应用［M］.北京：清华大学出版社，2004.

［12］Christian M Coviello.Source separation and tracking for time varying systems［D］.US：The Pennsylvania State U－niversity，the Graduate School，2005.

［13］Cichoki A，Amari S，Adachi M，Kasprzak W.Self－adaptive neural networks for blind separation of sources.［J］.IEEE international symposium on circuit and systems，1996（2）：157－161.

［14］Cichoki A，Orsier B，Back A，et al.On line adaptive algorithms in non－stationary environments using modified conjugate gradient approach［C］／／In Process of 1997 IEEE Workshop on NNSP.US：IEEE，1997：316－325.