水下火箭弹引信定距用涡轮流体动力特性

齐献山，李豪杰，沈德璋

（南京理工大学机械工程学院，江苏 南京 210094）

0 引言

小型水下潜艇等需要一种便于携带且杀伤力较大的武器作为自卫和攻击的手段。水下火箭弹由于体积小，对发射平台要求较低，爆破威力较大，所以非常适用于这一领域［1］。由于水下火箭弹速度快、射程较小，所以其解除保险可用的时间段很窄。因此需要一种体积小、精度较高的定距解除保险机构。

传统的引信延期解除保险方式主要有：火药延期、易熔合金、钟表机构、准流体延期［2－3］、气阻机构、球转子［4］、保险带及各种机电远解机构等。其中大部分是通过控制时间来实现在预定距离解除保险［2］。水下火箭弹在不同水深位置发射时其外弹道速度－时间曲线有较大变化，定时的方法难以获得较高的远解精度［3］。有部分迫弹、船舶运用涡轮进行延期解除保险或测量行进速度，但前者工作段在空气中，后者运动速度较低。涡轮在高速水下运动时的流体动力学性能参数未知。

由于高速水洞技术难度太大，目前国内水洞的最大流速只有18m／s［4］，远不能达到水下火箭弹工作速度，所以通过水洞实验的方法获得高速运动下的涡轮转动状态是不可行的。文献［5］对切向式涡轮流量传感器进行了三维流场仿真。和试验结果对比表明，模拟计算仪表系数相对误差最大值为7.51%。文献［6］对引信涡轮发电机的空气动力学、机械学、电磁学理论建立了数学模型，编制了仿真程序，进行了模拟。结果证明负载电压和弹速之间关系稳定，仿真结果对实验有很好的预测效果。以上文献说明仿真的方法对于涡轮在空气中运动的仿真是可行的，且精确度较高。本文研究的对象包围在水介质中，由于水相对于空气比重大、不可压缩。且水中受到湍流、空化等现象的影响，水中涡轮转动规律与在空气中存在很大差别。且水下火箭弹弹速较快，可达80m／s以上，其高弹速下涡轮转速特点和低弹速下有很大不同。

为获得涡轮在水下定距过程中的启动速度，涡轮转速和弹速对应曲线的线性度及其受水深环境的影响。通过ANSYS14.0中的ICEM和FLUENT模块对涡轮定距解除保险装置进行了仿真。得到了47组不同弹速、水压参数（该机构的常用工作环境）下的涡轮－弹速间的对应关系和受水深影响特性。

1 仿真方法

1.1 计算模型

1.1.1 涡轮外形

为减小涡轮对弹道的影响，本文涡轮模型的外轮廓和弹头保持一致。涡轮轮叶8片，附着在一个顶面直径8mm，底面直径13.88mm，高13mm的锥形台上，该结构可以有效增加涡轮推动力矩和表面压力，从而降低启动速度，减小空化面积［7］。轮叶厚度0.8mm，螺旋转角32°，如图1所示。

1.1.2 流场区域

根据水中流场分布特点，模型充分考虑了流场的扩散，在计算机能力允许的范围内，选取了较大流场区进行仿真。包含涡轮前180mm，后（含弹头）187 mm。为降低壁面影响，选流场直径为240mm（如图2所示）。为使网格在计算机计算能力范围内尽量的细致，选取该模型轴向的1／8扇形（一个轮叶所对角度）进行网格划分，通过周期性边界获得整体数据。

不难证明：在模型切割时，圆柱体截面的1／8扇形沿轴线投影落在扇形角平分线法线上时，所切得部分可以通过周期性旋转还原圆柱体。按照以上结论进行周期性建模，可以解决流场角度尖锐导致网格质量下降的问题。涡轮部分网格如图3所示。

图1 涡轮结构Fig.1 The structure of turbine

图2 仿真区域示意图Fig.2 Schematic diagram of simulation area

图3 中心区域网格分布图Fig.3 Central area grid

1.2 平衡条件

1.2.1 动力矩

涡轮转动的动力来源由涡轮表面压强对旋转轴的力矩积分得到，仿真计算结束后，可以通过软件的report选项自动积分得到该力矩的值。

1.2.2 阻力矩［8］

涡轮转动的阻力主要是轴承摩擦力矩。计算采用轴承设计中应用较普遍的Palmgren提出的算法。摩擦力矩M为载荷项M1和速度项M0的和。

M0反映了润滑剂的流体动力损耗，在运动粘度v（mm2／s）与转速n（r／min）的乘积vn≥2 000时

vn＜2 000时

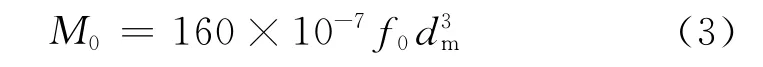
式（3）中，dm为轴承平均半径，dm＝ （d＋D）／2，d、D分别为轴承内、外直径；f0为与轴承类型和润滑方式有关的经验常数；n为轴承转速；v为在工作温度下润滑剂的运动粘度。

载荷项M1反映了弹性滞后和局部差动滑动的摩擦损耗，M1可按照下式计算

式（4）中，f1为与轴承类型和所受载荷有关的系数；P1为确定轴承摩擦力矩的计算载荷P1＝XFr＋YFa；其中Fr，Fa分别为轴承所受径向、轴向载荷，X，Y分别为径向、轴向系数。

1.2.3 启动速度

在启动速度仿真时，将涡轮转速设为0，在给定水深情况下，初定弹速值，根据仿真结果判断涡轮所受动力矩和静摩擦力大小，多次修改弹速使其达到平衡状态，得到该水深下的涡轮启动速度。静摩擦力矩采用Palmgren算法的M1项（由于轴承相对静止M0＝0）。

1.2.4 转动平衡状态

根据水下火箭弹的使用环境选取多组计算参数（包括弹速、水深等）。在一定的弹速、水深下，根据经验估计涡轮转速值进行仿真计算。据仿真结果计算推动力矩和摩擦力矩大小，据此修改涡轮转速的设定值。经过多次计算修改后得到涡轮受力平衡状态下的涡轮转速值。

2 仿真结果

2.1 涡轮转速随弹速的变化曲线

为了得到弹体速度和涡轮转速之间的关系，根据小型潜艇和水下火箭弹的工作特点，在水深20m处，弹速0～100m／s间选取了12个速度点进行仿真，得到涡轮转速－弹速对应关系，如图4所示。

由图4数据可见，在水深20m时涡轮启动速度约2.97m／s，在10～90m／s范围内涡轮转速和弹速间线性度良好。在速度小于10m／s和大于90m／s时线性度相对较差，但是变化平缓，偏离较小。

图4 涡轮转速随弹速变化曲线Fig.4 The rotational speed of the turbine with the projectile velocity curve

2.2 涡轮启动时的速度随水深的变化曲线

为获得涡轮的启动性能。在水深1～50m内选取了8组参数进行了仿真计算，结果如图5所示。

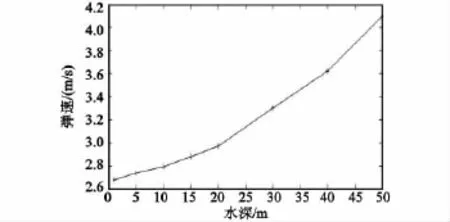
图5 涡轮启动速度与水深关系曲线Fig.5 The relationship between turbine start speed and water depth

涡轮启动时的弹速随水深增加有所上升，在水下50m水深以内，涡轮机构的启动速度小于4.1 m／s（约2.9m／s）。

2.3 涡轮转速随水深的变化曲线

为了验证水深条件对涡轮转速的影响，根据水下火箭弹主要工作阶段速度和水深，选取20m／s、40m／s、80m／s三种情况下，水深在1～50m 间分别进行仿真计算。最终结果如图6—图8所示。

由此可见在弹速20m／s情况下，随着水深的增加，涡轮转速降低。在弹速40m／s情况下，涡轮转速并不是随水深一致变化，而是先随水深的增加而增加，随后又随水深增加而减小。在弹速80m／s情况下，涡轮转速随水深变化较小。

图6 弹速20m／s时水深和涡轮转速对应曲线Fig.6 The outlet pressure and turbine speed curves under the projectile velocity of 20m／s

图7 弹速40m／s时水深和涡轮转速对应曲线Fig.7 The outlet pressure and turbine speed curves under the projectile velocity of 40m／s

图8 弹速80m／s时水深和涡轮转速对应曲线Fig.8 The outlet pressure and turbine speed curves under the projectile velocity of 80m／s

3 结果分析

3.1 涡轮转速与弹速关系分析

根据以上实验结果在速度小于10m／s和大于90m／s时线性度变差。分析原因为：弹速较低时，由于静压力以及启动摩擦力的影响，启动时速度不稳定且转速增加较慢。由于水下火箭弹工作速度远大于这个值，所以该区域的误差对定距没有影响，可以忽略。弹速较高时，水流的稳定性降低，且涡轮叶片附近出现较大面积的空化泡，造成涡轮转矩表面受力面减小，线性度下降。若进一步提高精度，可以根据实验及使用时积累的数据，建立弹速－涡轮转速表，每次获得涡轮转速数据后查表获得对应的弹速。根据以上数据利用最小二乘法拟合求得涡轮转速和弹速间的线性度为99.96%，线性度良好。

3.2 涡轮启动时的弹速度受水深的影响分析

由图5可见，涡轮启动时的弹速随水深增加而上升，分析其原因为：随着水深的增加涡轮表面受到的压力增大，摩擦力随之增加。涡轮启动时的弹速增加。在1～50m水深范围内，涡轮启动时的弹速不大于4.1m／s。由于水下火箭弹工作段弹道速度大于这个值，因此对定距解除保险没有影响。

3.3 涡轮转速受水深影响分析

误差计算方法为该情况下最大值与最小值之差与平均值之比：

式（5）中，ωmax为图中转速最大值。ωmin为图中转速的最小值。

弹速20m／s情况下，随着水深的增加，涡轮顶面压力增大，摩擦力增大，转速降低。据式（5）得水深变化引起的误差最大值约3.5%，由于水下火箭弹射程较短，误差积累值不大。

弹速40m／s情况下，水深较浅的情况下，涡轮周围压力较小，较易产生空化气泡，随着水深下降，涡轮表面压力增大，空化现象减弱，有利于涡轮转速的增加。但水深达到15m后，空泡已经很少，而且随水深增加涡轮轴承摩擦力会随着正压力的增加而增加，涡轮转速开始下降。如图9所示。根据式（5）计算得，在1～50m深范围内涡轮转速的变化不大于1.7%，误差较小。

图9 弹速40m／s时，水深1m、20m情况下空化现象对比Fig.9 Cavitation phenomenon contrast between water depth of 1mand 20munder the projectile velocity 40m／s

弹速80m／s情况下，由于弹体运动产生的压力远大于由于水深增加而增大的压力，所以涡轮转速随水深变化很小。根据式（5）计算得，最大误差约为0.1%，使用中可以忽略。

由以上分析可知，随弹速增加涡轮转速受水深的影响变小。这与弹速增加时弹体表面压力增加，水深产生的压力比重减小一致。根据某火箭弹弹速分布估算得，整体误差约为2.4%。

3.4 仿真方法分析

叶轮的流动是非常复杂的，要想准确地了解和掌握内部的流动规律很困难。CFD能够很好地解决内部流动计算所遇到的问题。FLUENT是目前功能最全、适用性最广、国内使用最广泛的CFD软件之一，具有灵活的网格特性，可以精确计算多种情况下的流体力学仿真。国内外许多科研工作者利用CFD数值仿真模拟技术，研究了内部流动状况［9］。由此可见该方法所得的结果可信度较高。

4 结论

本文通过仿真得到了涡轮在水下火箭弹引信定距结构中应用的特性。由仿真数据可见，涡轮定距保险机构中，涡轮启动速度较低（水深20m时约2.97m／s），涡轮转速和弹速之间线性度良好，在水深0～50m、弹速10～100m／s内，由水深产生的误差约为2.4%。分析表明该仿真方法成熟、结果可信度较高，数据中存在的问题有合理的解释，对于水下火箭弹定距误差较小，可以在设计中应用。

仿真的不足之处在于软件仿真数据会和实际情况存在偏差，因此需要实际弹道参数予以矫正。如果下一步能够获得全面的弹道数据就可以建立涡轮转速和弹速对应函数，就可以提高定距精度。

［1］石秀华，王晓娟.水中兵器概论［M］.西安：西北工业大学出版社，2005.

［2］石庚辰，李华.引信 MEMS远距离解除保险机构［J］.探测与控制学报，2008，30（3）：1－4.SHI Gengchen，LI Hua.Fuze＇s MEMS delay arming device［J］.Journal of Detection ＆ Control，2008，30（3）：1－4.

［3］沈德璋，张合，李豪杰.基于数值仿真的水下火箭弹引信远解机构取压点优选［J］.弹道学报，2010，12（4）：36－44.SHEN Dezhang，ZHANG He，LI Haojie.Pressure detection point optimization for delay arming device of underwater rocket fuze based on numerical simulation［J］.Journal of Ballistics，2010，12（4）：36－44.

［4］李淼，罗凯，胡峰，等.水洞超空泡人工通气控制系统设计［J］.计算机测量与控制，2011，19（9）：2 151－2 153.LI Miao，LUO kai，HU Feng，et al.Artificial ventilation control system for water tunnel supercavitation vehicle［J］.Computer Measurement ＆ Control，2011，19（9）：2 151－2 153.

［5］王振，张涛，徐英.测量小流量的切向式涡轮流量传感器的仿真与实验［J］.天津大学学报，2007，40（9）：1 048－1 053.WANG Zhen，ZHANG Tao，XU Ying.Simulation and experiment on tangential type turbine flow sensor for measurement of low flow rate［J］.Journal of Tianjin University，2007，40（9）：1 048－1 053.

［6］朱继南，林桂卿.引信涡轮发电机弹道发电模型和计算［J］.兵工学报，1993，8（3）：31－37.ZHU Jinan，LIN Guiqing.Fuze turbine generator trajectory generation model and calculation［J］.Acta Armamentard，1993，8（3）：31－37.

［7］王献孚.空化泡和超空化泡流动理论及应用［M］.北京：国防工业出版社，2009.

［8］张松林.最新轴承手册［M］.北京：电子工业出版社，2007.

［9］吴玉林.叶片泵设计与实例［M］.北京：机械工业出版社，2011.