基于压缩感知的认知雷达高分辨成像
孙凤莲,张 群,罗 迎,顾福飞,朱 丰
(空军工程大学信息与导航学院,陕西 西安 710077)
0 引言
传统雷达通常采用固定的发射信号,并通过接收端的自适应处理及滤波算法的设计来提高系统性能。对于日益复杂的电磁环境和密集杂波、多目标背景等挑战,当环境发生变化时,仅靠接收端的自适应处理已很难获得理想的成像效果。同时,当前的硬件技术水平(如相控阵雷达)也已为实现雷达系统发射端的自适应提供了良好的基础。在此背景下,加拿大的S.Haykin教授于2006年首次提出了“认知雷达”的概念[1],并已逐渐引起了雷达领域学者的注意与兴趣。参考国内外已有的对于认知雷达最优波形设计方法的研究[2-3],本文从目标所处成像环境对成像精度的不同要求出发,提出了一种基于压缩感知的认知雷达高分辨成像方法。
1 基于压缩感知的稀疏线性调频步进信号高分辨距离像
压缩感知[4](Compressive Sensing,CS)是近年来提出的一种全新的信号处理理论,目前已被广泛应用于高分辨成像雷达[5-7]中,为解决雷达成像中高分辨率与高采集率之间的矛盾提供了有效途径。其中,稀疏线性调频步进信号(SFCS)是常用的一种信号形式,其构成相当于随机保留原SFCS脉冲串内的一部分,即M( M<N)个子脉冲,载波步进频率=Li·Δf,且满足L1=0,LM=N-1。设雷达成像过程中共需要发射MT个脉冲串,其第m个脉冲串的第i个子脉冲信号为:

式中,t′=t-mNTr-iTr,fc+iΔf是第i个子脉冲的载频,μ为调频斜率,T1为子脉冲宽度。
按传统方法对回波信号在距离向作“dechirp”处理,得到目标回波的稀疏表示形式为:
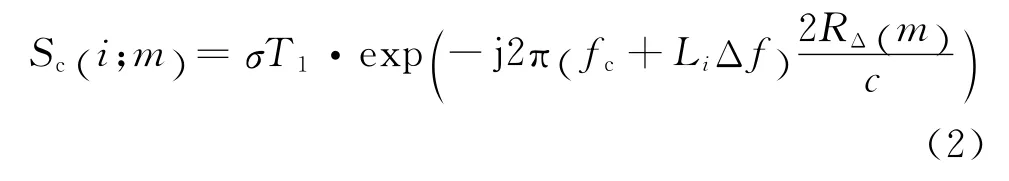
此时,由于信号载频不是按规律步进的,利用传统方法已无法得到目标的高分辨距离像(HRRP)。但如果目标上散射点在距离向是离散的,则信号Sc(i;m)在频谱上将是稀疏的[8],可通过CS理论对其进行重构处理。设目标的径向信息即HRRP为S (Ff;m),建立稀疏基矩阵Ψ ,具体形式为:
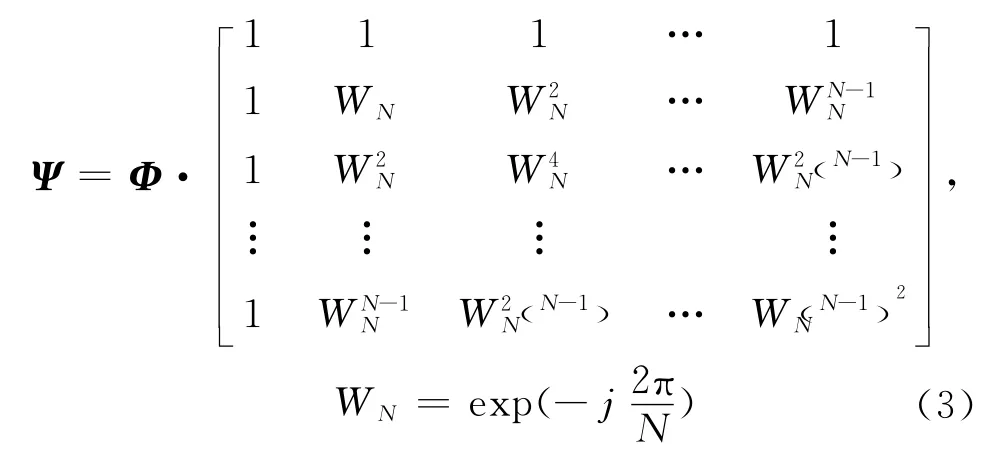
式中,Φ为随机部分单位矩阵,且满足

文献[8]从理论上证明了基于随机采样并利用部分DFT矩阵重构稀疏信号的可行性。所以,只要观测维数足够大,采用正交匹配追踪(Orthogonal Matching Pursuit,OMP)算法即可以高概率重构出目标径向信息S (Ff;m)。OMP算法的重构质量与观测维数有关。一般地,当观测维数M满足以下不等式时,通过该算法即可高概率的重构出原始信号[9]
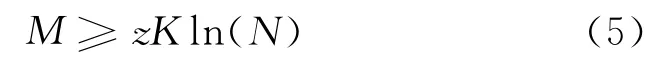
式中,z为较小的常数。
2 基于压缩感知的认知雷达自适应稀疏成像
在第1章成像方法中,M作为稀疏SFCS的一个重要参数,与目标散射点的稀疏度K密切相关,也即在利用CS对目标HRRP进行重构时,极可能需要目标稀疏度K这一先验知识。这与认知雷达的理论基本是一致的,因而可利用接收端到发射端的反馈信息自适应地调整对K的估计值,进一步调整发射信号波形,实现与目标环境的最优匹配。

式中,Sc1(k)和Sc2(k)为相邻两次目标距离像。设经验门限值Th,若cr<Th,则认为对K的估计值较小,后续需增大;反之,则认为估计值较大,可利用重构的目标HRRP实现对目标当前稀疏度的认知。同时,为克服OMP算法的重构误差,在对cr进行计算时,选用相邻多次(设为m次)目标高分辨距离像的平均值代替单次高分辨距离像。其具体成像过程为:
1):依照文献[10]中的方法,发射一个仅含有少量(设为N′)子脉冲的传统SFCS脉冲串,得到目标的一个粗分辨HRRP,并大致估计目标径向稀疏度(i =0)。
4):通过式(6)计算相邻目标HRRP的相关系数cr,若cr<Th,则令=+a(a>0);反之,则计算重构HRRP中幅值较大的散射点的数Ki,并令=Ki。
5):对目标像重构次数进行判断。若i<MT,则令i=i+1,并转2);否则,把重构得到的MT个序列按顺序排成矩阵= [,…,],完成对目标HRRP的认知成像。
3 仿真验证
为验证本文成像方法的有效性,采用图1飞机散射点模型进行仿真。该模型径向长度约16m,径向上的散射点坐标数约50个。初始时刻与雷达的距离为10km,飞行速度为300m/s。雷达发射信号为SFCS,载频为10GHz,脉冲串重复频率PRF=250Hz,频率步进阶数N=512,频率步进量Δf=2.343 8MHz,合成带宽B=1.2GHz,对应距离分辨率Δr=0.125m。设定目标成像时间为2s,成像过程中共发射500个脉冲串,获得方位向分辨率Δa=0.25m。

图1 飞机目标散射点模型Fig.1 Scatter model of the air target
雷达发现目标后,首先发射一组含有少数子脉冲的传统SFCS,这里取N′=17,对应的距离分辨率Δr′=3.765m,采用传统方法合成目标的一个粗分辨HRRP,如图2(a)所示。取距离像幅度的阈值Tα=0.2,得到目标的径向长度估计值为5个距离单元,即≈18.825m,此时,对应的稀疏度最大值Kmax=/Δr≈150。设对目标距离向稀疏度的初始估计值为=20 (<Kmax),由公式(5)得到=138,通过OMP算法重构得到目标的一个HRRP如图2(b)所示。显然,由于对目标稀疏度的估计值太小,两次得到的目标HRRP重构误差均较大,且相似度很低,在后续成像过程中需增大对K的估计值。

图2 目标粗、高分辨距离像Fig.2 Target's Coarse-RRP、target's HRRP
仿真实验中,分别取m=10,a=3,Th=0.9。由图3(a)可以看出,在本次成像过程中,系统根据对目标径向稀疏度K的认知实现了对自身参数的50次调整,并使cr始终保持在0.85~0.95之间。图3(b)为通过该认知方法重构出的第200个HRRP,它有效地描述了飞机目标在距离向上的特征。对图3(a)所示自适应稀疏条件下重构得到各次目标HRRP作方位向的傅里叶变换,即可得到目标ISAR二维像,成像结果如图3(c)所示。可以看出,在满足成像精度的前提下,本次成像过程中信号子脉冲数量的减少十分明显,平均每次利用的稀疏子脉冲数为211个,仅占512个可用子脉冲数的41.21%,有效节省了雷达频谱资源。
在认知雷达系统中,发射波形不仅能够根据目标稀疏特性自适应调整,而且能够根据当前任务及目标所处环境进行最优配置。在多任务条件下,对系统处理的实时性要求相对较高而对目标成像精度的要求相对较低,此时,可通过降低T2值的设置来实现,如取T2=0.75,得到雷达自适应稀疏成像结果如图4所示。与图3相比,在该成像精度要求下,雷达成像所需子脉冲数更少,仅为149个,大幅节省了雷达频谱资源。但由于观测次数较低,重构出的目标ISAR像有部分散射点缺失,但并不影响对目标的有效识别。
以上仿真实验都是基于无噪条件下进行的,但通常,目标所处环境都有一定的噪声存在。当雷达接收端信噪比为-5dB时,其相应的稀疏度估计及频谱自适应稀疏曲线如图5(a)所示,得到的ISAR成像结果如图5(b)所示。可知,在本次成像过程中,由于目标信号共经过了两次能量的相干积累,成像质量并未受到噪声影响,但由于噪声的存在,为达到相邻相关系数Th=0.9的成像精度,平均每次发射SFCS脉冲串中的稀疏子脉冲数为283个,较无 噪条件下更多,符合目标成像的实际环境。

图3 基于CS的认知雷达高分辨成像Fig.3 High-resolution imaging of cognitive radar based on CS
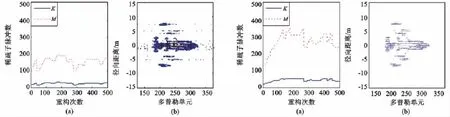
图4 T2=0.75时的认知雷达成像(M=149)图5 噪声条件下的认知雷达成像(M=283)Fig.4 Imaging of cognitive radar in T2 =0.75(M =149)Fig.5 Imaging of cognitive radar in noise environment(M =283)
表1给出了利用本文所提方法和传统方法所得结果的比较。可以看出,为获得成像所需的500个飞机目标的HRRP,通过本文方法,无论在高精度要求、低精度要求还是噪声环境中,都能够自适应地调整雷达信号波形,充分利用雷达频谱资源。同时,通过本文方法成像还有效减少了系统运算时间,增强了雷达系统的实时处理能力。
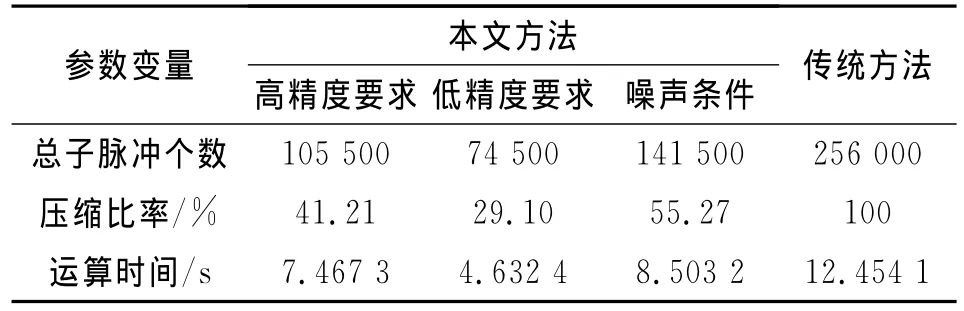
表1 系统性能比较Tab.1 Comparison of the system's capability
4 结论
本文结合认知雷达的信息反馈回路,提出了基于压缩感知的认知雷达高分辨成像方法。该方法首先对成像目标稀疏度进行了大致估计,其次根据重构得到的目标距离像之间的相关系数自适应地调整后续发射信号波形,逐步实现对目标距离向信息的认知,最后对重构得到的各次高分辨距离像通过传统方法进行压缩,得到了目标的高分辨二维像。仿真表明:与传统方法相比,本文所提方法充分利用了目标所处环境信息自适应调整发射信号波形,更具有智能化特点,且需要更短的系统运算时间,更适合于日益复杂的电磁环境。
[1]Haykin S.Cognitive radar:a way of the future[J].IEEE Signal Processing Magazine,2006,23(1):30-40.
[2]Goodman N A.Closed-loop radar with adaptively matched waveforms[C]//2007International Conference on Electromagnetics in Advanced Applications.Torino,Italy,2007:468-471.
[3]范梅梅,廖东平,丁小峰,等.基于 WLS-TIR的多目标识别认知雷达波形自适应方法[J].电子学报,2012,40(1):73-77.FAN Meimei,LIAO Dongping,DING Xiaofeng,et al.A-daptive waveform design based on wls-tir for multiple targets recognition in cognitive radar[J].Acta Electronica Sinica,2012,40(1):73-77.
[4]Donoho D L.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1 289-1 306.
[5]Y S Yoon,M G Amin.Compressed sensing technique for high-resolution radar imaging[J].Proceedings of SPIE,2008,6968(1A):1-10.
[6]L Zhang,M D Xing,C W Qiu,J Li,J L Sheng,Y C Li,Z Bao.Resolution enhancement for inversed synthetic aperture radar imaging under low SNR via improved Compressive Sensing[J].IEEE Transactions on Geoscience and Remote Sensing,2010,48(10):3 824-3 838.
[7]Michael Leisnering,Christian Debes,Abdelhak M.Zoubir.Compressive sensing in through-the-wall Imaging[C]//International Waveform Diversity and Design Conference(WDD),2010:150-154.
[8]Candes E,Romberg J,Tao T.Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information[J].IEEE Trans on Info Theory,2006,52(2):489-509.
[9]Kunis S,Rauhut H.Random sampling of sparse trigonometric polynomials II:Orthogonal matching pursuit versus basis pursuit[J].Foundations of Computational Mathematics,2007,8(6):737-763.
[10]Ying Luo,Qun Zhang,Cheng-wei Qiu,Xian-jiao Liang,Kai-ming Li.Micro-Doppler effect analysis and feature extraction in ISAR imaging with stepped-frequency chirp signals[J].IEEE Transactions on Geoscience and Remote Sensing,2010,48(4):2087-2098.

