基于差分的磁偶极子单点张量定位方法

李 光，随阳轶，刘丽敏，林 君

（吉林大学仪器科学与电气工程学院，吉林 长春 130026）

0 引言

根据磁场的叠加原理，磁偶极子作为最基本的磁单元，目前已被广泛应用于磁性目标的建模及定位当中［1－6］。Wynn于1971年提出了利用磁张量对磁偶极子进行定位跟踪的算法［2］。磁张量方法具有很多磁总场、磁矢量方法所没有的优点如受磁化方向影响小、具有较多的细节能够用于三维定量反演解释等，在军事、环境、资源勘探等方面有着广阔的应用前景［7］。常规采用单点测量的磁场矢量及磁张量数据对磁偶极子进行定位的方法，由文献［8—10］分别得出，与其他定位方法相比只需要单点观测即可达到定位的目的，能够减少解的非唯一性，不需要增加更多的观测量［11］，却受地磁场干扰大，极大地限制了其应用范围［5］。基于此，本文提出了基于差分的消除地磁场干扰的磁偶极子单点张量定位方法。

1 单点磁张量定位

磁场的三个分量 （Bx，By，Bz）在空间xyz三个方向的导数构成了磁张量，共包括九个要素［2］，记为G，表示如下：

在现实测量中，可以利用差分来替代微分：

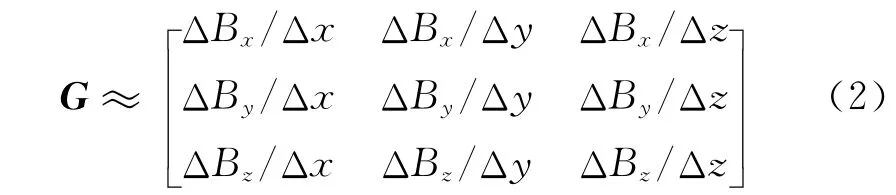
由Maxwell方程可知，B场的散度及旋度为零，即张量矩阵具有无迹性与对称性，得：

由文献［8—10］推导出磁偶极子的位置信息与单点处所测量的磁场矢量及磁张量之间的线性关系。通过设计出相应的磁张量系统结构如图1所示，坐标系采用大地坐标系即x向为正北方向，y向为正东方向，z向为垂直向下，在未考虑地磁场干扰的情况下验证了其可行性［4］。

图1 磁张量系统结构Fig.1 Structure of magnetic tensor system

由式（4）可知，在已知某点处磁张量的九个要素及相应的磁偶极子所产生的三分量磁场值Bx，By，Bz就可得到磁偶极子的位置信息，如式（5）所示。

式（5）即为原方法的定位理论，但是由于Bx，By，Bz为磁偶极子在某一点处所产生的磁场矢量，在地磁场存在的情况下，很难获得其测量值，极大地限制了其应用范围，本文通过采用差分的方法，能够消除地磁场及其他共模干扰，增加了其在现实探测中的实用性。

2 基于差分的单点磁张量定位

为了能够消除地磁场及其他共模干扰的影响，则必须消除式（5）中磁场矢量项，本文采用差分的方法并设计出相应的磁张量测量系统，实现这一想法。

2.1 磁张量测量系统

为了便于阐述，本文先给出所设计的磁张量系统（如图2所示），它是由6个高精度矢量传感器构成，且处于同一平面内，相邻传感器的间距为d，图2所示M为磁偶极子的磁矩矢量，r中的rx，ry，rz为定位所要求取的参数值，所示坐标系为大地坐标系。

图2 磁张量系统定位示意图Fig.2 Positioning Diagram of Magnetic Tensor System

2.2 基于差分的单点张量定位原理

Bxi，Byi，Bzi：第i探头处磁场分量值，i＝0，…，5。

Bxxi，Bxyi，Bxzi，Byxi，Byyi，Byzi，Bzxi，Bzyi，Bzzi：第i探头处的9个张量值，i＝0，…，5。

Bxxxi，Bxyxi，Bxzxi，Byxyi，Byyyi，Byzyi，Bzxzi，Bzyzi，Bzzzi：第i探头处磁场的三阶导数值，i＝0，…，5。

rx，ry，rz：磁偶极子位置的三个分量。

式（4）两边分别对x，y，z求导，得：

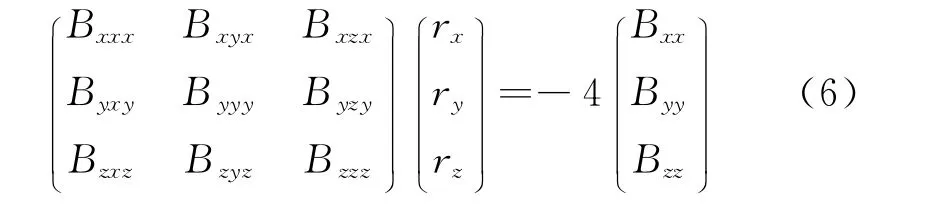
由方程组（3）可知，Bxyx＝Byxx，Bxzx＝Bzxx，Byxy＝Bxyy，Byzy＝Bzyy，因此可以通过0探头、1探头及3探头得到Bxxx0，Bxyx0，Bxzx0，Bxx0。同理，由0探头、2探头及4探头得到Byxy0，Byyy0，Byzy0，Byy0。以下以0探头、1探头及3探头的x轴分量Bx0，Bx1，Bx3求取Bxxx0，Bxx0为例进行说明。

已知0探头、1探头及3探头测得的磁场x轴分量Bx0＝Bx（x0），Bx1＝Bx（x0－d），Bx3＝Bx（x0＋d）得：

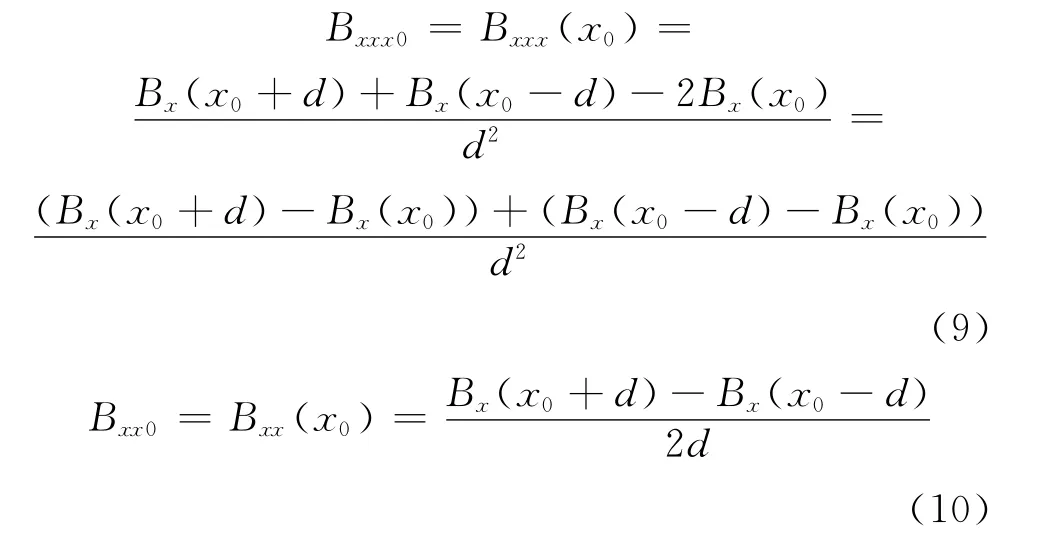
由于Bxx＋Byy＋Bzz＝0可知，式（6）中只有2个是有效的，取：

由0探头，1探头及5探头所测得的x轴分量得1探头处的Bxxx1，Bxyx1，Bxzx1，Bxx1，可知下式成立：Bxxx1rx＋Bxyx1ry＋Bxzx1ry＝－4Bxx1＋Bxxx1d （13）

综合式（11）、式（12）、式（13），我们能够得到rx、ry、rz的值：

可以看出式（14）对式（5）进行了改进，在式（14）中消除了磁场矢量项，利用差分的方法将式（14）右边所有的量均转化为磁场矢量的相应磁场分量之差，故在大程度上消除了地磁场以及其他共模干扰。

3 仿真及误差分析

将磁异常体等效成磁偶极子，并放置于坐标原点处，磁张量系统处于（10，10，－10）点处，取基线长度为d＝0.2m。假设地磁场的总场为50 000nT，取长春地区磁倾角、磁偏角分别为I＝60°，D＝－9°。不失一般性，取磁偶极子磁倾角、磁偏角分别为I＝45°，D＝45°。通过分析在不消除地磁场；利用基站消除地磁场，考虑距离的影响；利用基站消除地磁场，考虑系统运动造成的影响，对比原方法与本文方法的定位结果，并以所得到的rx、ry、rz与理想rx、ry、rz的绝对误差进行分析。

3.1 不消除地磁场

在不消除地磁场的情况下，认为系统中间点处矢量传感器测得的磁场为磁偶极子所产生的磁场。磁偶极子的磁矩大小由M＝2×102A·m2到M＝2×104A·m2变化，两种方法的定位误差如图3所示。

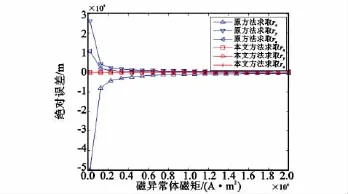
图3 磁矩改变，两种定位方法的定位误差Fig.3 Changes in magnetic moment，the positioning error of two positioning methods

由图3可知，本文提出的定位方法能够有效地消除地磁场，不受磁矩大小变化的影响，且具有较高的定位精度，rx，ry，rz的定位误差分别为0.000 4 m，0.000 4m，0.002 2m。原方法的定位误差会随着磁矩的增大而减小，而当磁矩大小为M＝2×104A·m2时，定位误差也达到上千米，可见在不消除地磁场的情况下，利用原方法进行定位是不可行的。

3.2 消除地磁场，考虑距离的影响

将与磁张量系统相距一定距离的基站测得的磁场矢量作为地磁场的测量值，系统中间点处测得的磁场矢量减去基站所测得的磁场矢量作为测得的磁偶极子产生的磁场矢量值，取地磁场总场梯度为0.02nT／m。

当磁偶极子磁矩大小为M＝2×103A·m2时，两种方法定位误差受距离变化的影响，如图4所示。

图4 距离改变，两种定位方法的定位误差Fig.4 Changes in distance，the positioning error of two positioning methods

当系统与基站相距1km时，磁偶极子的磁矩大小由M＝2×102A·m2到 M＝2×104A·m2变化，两种方法的定位误差，如图5所示。

图5 磁矩改变，两种定位方法的定位误差Fig.5 Changes in magnetic moment，the positioning error of two positioning methods

由图4、图5可知，本文提出的定位方法不需要利用基站来消除地磁场，不受磁矩大小变化的影响，且具有较高的定位精度，rx，ry，rz的定位误差分别为0.000 4m，0.000 4m，0.002 2m。而原方法由于受地磁场梯度的影响，在地磁场梯度一定时，其定位误差与基站的距离成正比，受磁矩的影响较大，当距离为1km，磁偶极子的磁矩大小为M＝2×103A·m2时，rx，ry，rz的定位误差分别为－19.965 7 m，10.501 9m，4.297 7m，因此利用基站来消除原方法中地磁场的干扰也是不可行的。

3.3 消除地磁场，考虑系统运动的影响

在假设地磁场梯度为0，利用基站能够消除地磁场的情况下，考虑系统运动，姿态发生变化，下面以横滚角的变化为例进行说明。

磁偶极子的磁矩大小为M＝2×103A·m2时，两种方法的定位误差受横滚角的影响，如图6所示。

图6 横滚角变化，两种定位方法的定位误差Fig.6 Changes in roll angle，the positioning error of two positioning methods

当系统横滚角为0.05°时，磁偶极子磁矩大小由M＝2×102A·m2到M＝2×104A·m2变化，两种方法的定位误差，如图7所示。

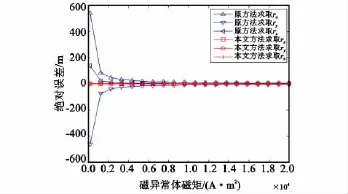
图7 磁矩改变，两种定位方法的定位误差Fig.7 Changes in magnetic moment，the positioning error of two positioning methods

由图6、图7可知，本文提出的定位方法具有较高的定位精度，且不受磁矩大小的影响。系统在地磁场中运动，横滚角变化较小时，两种方法的定位误差均与横滚角成正比，而原方法的定位误差受横滚角及磁矩的影响较大。当横滚角为0.05°，磁偶极子的磁矩大小为M＝2×103A·m2时，原方法求取的rx，ry，rz定位误差分别为54.201 5m，－46.415 1 m，13.802 0m，而本文方法求取的rx，ry，rz定位误差分别为0.418 2m，－0.596 6m，－0.428 4m，可见原方法在地磁场存在的情况下，基本无法在运动平台上应用。

4 结论

本文通过对原单点磁张量定位中利用磁场矢量及磁张量数据进行磁偶极子定位的方法进行改进，提出基于差分消除地磁场干扰的磁偶极子单点磁张量定位方法，进而设计出基于该定位方法的磁张量测量系统。通过仿真可知，在地磁场存在的情况下原方法基本无法实现磁偶极子的定位，而本文的定位方法由于采用差分方式，有效地消除了地磁场及其他共模干扰，具有较高的定位精度。本文方法也存在一些不足，需要进一步的完善，由其定位原理可知，系统的定位精度受非共模干扰，如磁矢量传感器之间的不一致性，系统结构的安装误差等影响大，因此需要对它们进行校正，国内外在这方面已经有一些很好的尝试［12－13］，这些工作正是以后的研究重点。

［1］Wynn W，Frahm C，Carroll P，et al.Advanced superconducting gradiometer／magnetometer arrays and a novel signal processing technique［J］.Magnetics，IEEE Transactions on，1975，11（2）：701－707.

［2］Wynn W M.Magnetic dipole localization using the gradient rate tensor measured by a five－axis magnetic gradiometer with known velocity［C］／／Orlando，FL.USA：SPIE，1995.

［3］唐劲飞，龚沈光，王金根.磁偶极子模型下目标定位和参数估计的两种新方法［J］.电子学报，2003（1）：154－157.TANG Jinfei，GONG Shenguang，WANG Jingen.Two new magnetic localization and parameter estimation methods under the dipole model［J］.Acta Electronica Sinica，2003（1）：154－157.

［4］张朝阳，肖昌汉，阎辉.磁性目标的单点磁梯度张量定位方法［J］.探测与控制学报，2009（4）：44－48.ZHANG Zhaoyang，XIAO Changhan，YAN Hui.Localiza－tion of a magnetic object based on magnetic gradient tensor at a single point［J］.Journal of Detection ＆ Control，2009（4）：44－48.

［5］Niu Jun，Teng Baohua，Yin Wenzhao.Localization of a single－point magnetic target in the special geomagnetic field［C］／／Third International conference on Measuring Technology and Mechatronics Automation，2011：411－417.

［6］杨明明，刘大明，连丽婷，等.用海面磁偶极子源定位海底矢量磁传感器［J］.探测与控制学报，2011，33（5）：41－45.YANG Mingming，LIU Daming，LIAN Liting，et al.Underwater vector－magnetometer located by using magnetic dipole sources in the offing［J］.Journal of Detection ＆Control，2011，33（5）：41－45.

［7］吴招才，刘天佑.磁力梯度张量测量及应用［J］.地质科技情报，2008（3）：107－110.WU Zhaocai，LIU Tianyou.Magnetic gradient tensor：its properties and uses in geophysics［J］.Geological Science and Technology Information，2008（3）：107－110.

［8］肖昌汉，何华辉.磁性物体探测的线性求解方法［J］.华中理工大学学报，1997（9）：84－86.XIAO Changhan，HE Huahui.A linear method for detecting a magnetic object［J］.Journal of Huazhong University of Science and Technology，1997（9）：84－86.

［9］Nara T，Suzuki S，Ando S.A closed－form formula for magnetic dipole localization by measurement of its magnetic field and spatial gradients［J］.Magnetics，IEEE Transactions on，2006，42（10）：3 291－3 293.

［10］Schmidt P W.Inversion using Euler deconvolution of the magnetic gradient tensor［J］.ASEG Extended Abstracts，2006（1）：1－3.

［11］吴招才，刘天佑，高金耀.磁力梯度张量及在磁偶极子定位中的应用［C］／／地球物理与海洋安全.北京：中国地球物理协会，2009.

［12］Bracken R E，Smith D V，Brown P J，et al.Calibrating a tensor magnetic gradiometer using spin data［M］.US：US Geological Survey，2005.

［13］Sui Yangyi，Wang Shilong，Meng Hui，et al.An Analysis and Elimination of Zero Drift in Magnetic Gradient Tensor Exploration System［C］／／Third International conference on Measuring Technology and Mechatronics Automation.Shanghai：ICMTMA，2011：371－374.