多元指数插值响应面方法分析复杂结构可靠度

程 晔，周翠英，黄林冲，文建华

中山大学工学院，广州510275

复杂结构可靠度分析中难以直接得到功能函数的解析表达式，普通的快速概率积分法无法求解.目前的蒙特卡洛 (Monte Carlo，MC)方法，包括在此基础上改进的各种抽样模拟方法，可解决此类复杂问题，但要达到较高精度仍需要大量样本，计算量太大，难以实际应用.随机有限元方法不易编程实现，对非线性问题和随机变量变异系数大的情况，误差仍较难控制.响应面方法 (response surface method，RSM)最早由 Box和 Wilson提出［1］，具有思路简明、计算量小、精度较高等特点，是目前最具生命力的复杂结构可靠度分析方法之一.该方法目前已经发展了多种响应面函数形式，如二次多项式［2-5］、神经网络［6-8］和支持向量机［9-13］等.对于非线性较强的隐式功能函数，普通二次多项式难以有效逼近原函数，神经网络和支持向量机响应面方法在构造过程中对样本点个数和布置仍存在较强的依赖性，求解精度不易控制.本研究采用具有较强非线性逼近能力的指数型插值基函数，发展一种基于多元指数插值的响应面方法，构造了相应的迭代求解格式，以控制求解精度，并通过典型算例验证其求解精度和效率.

1 多元指数插值响应面的构造

1.1 多元指数插值函数

多元函数F(x)=F(x1，x2，…，xn)在m个点上的函数值分别为z1、z2、…、zm，可用指数插值函数 f(x)逼近原函数 F(x)［14］，

其中，

ζ和ρ为两个待定参数.插值函数f(x)连续可微，容易验证，无论ζ和ρ如何取值，均有f(xi)=zi，即保证插值函数f(x)总能通过所有插值点.

插值函数f(x)逼近原函数F(x)的程度取决于两个待定参数ζ、ρ以及插值点的数量和分布.下面给出待定参数ζ和ρ的确定方法.

1.2 指数插值函数响应面的参数确定

首先取

则插值函数f(x)还剩下一个待定参数ρ.若用

表示插值函数集合，其中G表示整个插值区域，G1表示非插值点集合，则ρ的取值应使插值函数f(x)在非插值点上尽量接近原函数，即

由于F(x)是未知函数，式 (9)的范数无法计算，但可通过优化目标函数来确定ρ，

也就是说，具体计算中，除m个插值点外，再另取r个点，使得在此r个点上的插值函数f(xj，ρ)与原函数之差，在式(10)目标函数意义下最小.

2 插值点的选取

2.1 插值点布点区域

在结构可靠度分析中，先用R－F法将原始随机变量空间变换至标准正态空间.根据可靠度分析一般原则，插值点布点区域取 ±3σi=±3.对于一个3变量的多元函数，其布点区域为一个边长为6的立方体.

2.2 插值点的正交表法布置

正交实验设计 (orthogonal experimental design)是研究目标与多因素多水平关系的实验设计方法之一［15］，它根据正交性从全面实验中挑选出部分有代表性的点进行实验，这些有代表性的点具备“均匀分散，齐整可比”的特点，采用正交实验设计形成的试验点表格也称为正交实验表.如果考虑一个3因素，每个因素按7水平设计，所需样本点个数为49个，具体布点如表1.如果按照网格点法，考虑3因素7水平网格布点，需要的样本点个数为个点，正交表法将样本点个数大大减少.若采用3因素5水平设计，可将样本点个数减少到25个，如表2.作为工程实际应用而言，这样的分析工作量更容易接受.后面的分析均采用5水平正交实验表来确定插值点.

表1 3因素7水平正交实验布点表Table 1 Distribution table of orthogonal experiment with three factors and seven levels

表2 3因素5水平正交实验布点表Table 2 Distribution table of orthogonal experiment with three factors and five levels

2.3 校核点的布置

由于求解本研究建立的多元插值响应面还需r个点，采用随机投点法处理.给定区域为

Ri(t)为区域［－3σi，3σi］上服从均匀分布的随机过程，则初始插值点集合为

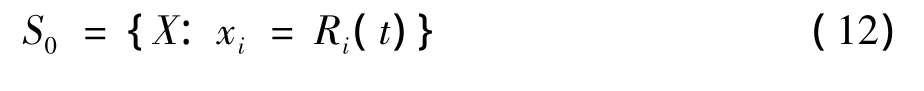
3 可靠度指标求解

将上述指数插值函数响应面构造方法用于复杂结构工程可靠度分析，具体步骤为:

①利用R－F法将非正态随机变量X当量正态化成X'，其均值为μX'，标准差为σX'，协方差矩阵为VX';

②将独立正态的随机变量Y'标准化为Y;

③采用正交表法和有限元法生成插值点，建立隐式函数的指数插值函数f(x)，按照多因素5水平布点，另外再增加一组随机投点，投点个数取3，以式 (10)为目标函数，利用Matlab优化工具箱得到指数插值函数的待定参数ρ值，确定f(x);

④利用常用的可靠度求解方法求解验算点y*(k)和可靠度指标 β(κ);

⑤计算验算点原函数值F(y*(k))，将其增加到插值点集合，修正插值函数f(x)，如前后两次可靠度指标满足收敛条件，则输出f(x)、y*(k)和β(k).否则，返回步骤③迭代计算.

根据上述求解思路，采用Matlab软件编制程序，其中指数插值函数系数ρ和可靠指标求解均利用Matlab提供的优化工具箱求解.

4 算例分析

为检验本研究指数插值响应面方法的有效性，选取3个不同类型的数值算例.算例1极限状态方程为二次型，引自文献 ［8］;算例2极限状态方程为三次型;算例3极限状态方程为指数型，算例2和算例3均引自文献 ［16］.

算例1 极限状态方程z=x1x2－x3，其中随机变量 x1～ N(0.547 2，0.027 4)，x2～ N(3.8，0.304)，x3～N(1.3，0.91)均服从正态分布.

分别采用一次二阶矩法、二次序列响应面方法和桂劲松等［8］建立的改进神经网络响应面方法，与本研究方法做对比分析，结果如表3.对于该算例，这几种方法均较精确找到原函数的验算点，求解的可靠度指标也极为接近，但本研究方法和桂劲松的改进神经网络方法，在调用原函数的次数上相对二次序列响应面方法有一定优势.

表3 本研究方法与其他方法比较 (二次型)Table 3 Results comparison of the proposed method with other methods(quadratic form example)

算例2 极限状态方程g(x1，x2)=x31+x32－4.0，其中，随机变量满足x1～N(3.0，1.0)，x2～N(2.9，1.0).分别采用一次二阶矩法、二次序列响应面法、改进二次响应面法［16］和本研究建立的多元指数插值响应面法计算，结果如表4.由表4可见，本研究方法计算得到的验算点、可靠度指标均与采用一次二阶矩法、改进的二次响应面法结果非常接近，说明本研究方法具有较高的计算精度，而一般二次响应面法得到的结果与这3种方法的计算结果略有差异，反映出二次响应面在逼近非线性更强的原极限状态曲面时存在一定误差.同时，本研究方法和改进二次响应面法的原函数调用次数均为17次，而二次序列响应面方法为35次，也说明了本研究方法计算效率较高.

表4 本研究方法与其他方法比较 (三次型)Table 4 Results comparison of the proposed method with other methods(cubic form example)

算例3 极限状态方程z=exp(1+x1－x2)+exp(5－5x1－x2)－1，其中，随机变量和均服从标准正态分布.该算例为一常用来考核隐式极限状态可靠度分析方法精度的指数型极限状态函数.由于该算例非线性程度非常高，采用一次二阶矩法和一般二次响应面方法求解，迭代都不收敛.表5给出了改进的二次响应面方法［16］、贡金鑫采用的二次二阶矩法［17］和本研究方法的计算结果.3种方法计算的验算点和可靠度指标均十分接近，说明本研究方法具有较高的精度.从原函数调用次数上看，本研究方法在该算例上体现出了极高的效率.

表5 本研究方法与其他方法比较 (指数型)Table 5 Results comparison of the proposed method with other methods(exponential form example)

结 语

本研究在分析目前隐式极限状态方程可靠度分析的各类响应面方法特点的基础上，探讨了一类新的基于多元指数插值函数响应面的构造方法，并将其用于隐式极限状态方程可靠度分析，研究表明:

①进一步证实了各种多元函数插值方法均可用于构造隐式功能函数的响应面，各类方法求解精度和效率不仅取决于方法本身，还与原隐式功能函数形态密切相关;

②提出了一类新的指数插值函数响应面方法，并给出了相应求解可靠度指标的求解方法和步骤，从而建立了基于多元指数插值函数响应面的可靠度分析方法，通过数值算例证实了该方法对非线性强的原始功能函数逼近能力较强，具有较好的精度与效率.

/References:

［1］ WONG F S.Slope reliability and response surface method［J］.Journal of Geotechnical Engineering，1985，111(1):32-53.

［2］ Bucher C G，Bourgund U.A fast and efficient response surface approach for structural reliability problems［J］.Structural Safety，1990，7(1):57-66.

［3］ TONG Xiao-li，ZHAO Guo-fan.The response surface method in conjunction with geometric method in structural reliability analysis ［J］.China Civil Engineering Journal，1997，30(4):51-57.(in Chinese)佟晓利，赵国藩.一种与结构可靠度分析几何法相结合的响应面方法［J］.土木工程学报，1997，30(4):51-57.

［4］ SU Yong-hua，FANG Zu-lie，GAO Qian，Reliability analysis on special underground rockmass by response surface method ［J］.Rock Mechanics and Engineering，2000，19(1):55-58.(in Chinese)苏永华，方祖烈，高 谦.用响应面方法分析特殊地下岩体空间的可靠性 ［J］.岩石力学与工程学报，2000，19(1):55-58.

［5］ SU Yong-hua，WANG Xu-chun，ZHANG Zong-she.Response surface method of rock mass engineering stability reliability analysis and its application ［J］.Journal of Engineering Geological，2001，9(4):381-386. (in Chinese)苏永华，王旭春，张宗社.岩体工程可靠性分析的响应面方法及其应用 ［J］.工程地质学报，2001，9(4):381-386.

［6］ Mandal S，Sivaprasad P V，Venugopal S.Artificial neural network modeling of composition-process-property correlations in austenitic stainless steels［J］.Materials Science and Engineering，2008，485(1/2):571-580.

［7］ Cheng J，Li Q S，Xiao R C.A new artificial neural network-based response surface method for structural reliability analysis ［J］.Probabilistic Engineering Mechanics，2008，23(1):51-63.

［8］ GUI Jin-song，KANG Hai-gui.Improved BP ANN response surface method for structure reliability analysis［J］.Applied Mechanics，2005，22(1):127-131.(in Chinese)桂劲松，康海贵.结构可靠度分析的改进BP神经网络响应面法 ［J］.应用力学学报，2005，22(1):127-131.

［9］ JIANG Xiang-hua，YANG Xiao-guang，WANG Yanrong.An iterative RBF ANN response surface method for structural reliability analysis ［J］.Aerospace Power，2008，23(1):26-31.(in Chinese)蒋向华，杨晓光，王延荣.结构可靠度逐步逼近径向基神经网络响应面法 ［J］.航空动力学报，2008，23(1):26-31.

［10］ LI Hong-shuang，LU Zhen-zhou.A support vector machine response surface method for structure reliability analysis［J］.Computational Mechanics，2009，26(2):199-203.(in Chinese)李宏双，吕震宙.结构可靠性分析的支持向量机响应面法 ［J］.计算力学学报，2009，26(2):199-203.

［11］ JIN Wei-liang，TANG Chun-xi，CHEN Jin.SVM based on response surface method for structural reliability analysis［J］.Computational Mechanics，2007，24(6):713-718.(in Chinese)金伟良，唐纯喜，陈 进.基于SVM的结构可靠度分析响应面方法 ［J］.计算力学学报，2007，24(6):713-718.

［12］ LI Hong-shuang，LU Zhen-zhou，ZHAO Jie.A Support vector machine method for reilbility analysis based on weighted linear response surface［J］.Engineering Mechanics，2007，24(5):67-71.(in Chinese)李洪双，吕震宙，赵 洁.基于加权线性响应面法的支持向量机可靠性分析方法 ［J］.工程力学，2007，24(5):67-71

［13］ JIN Wei-liang，YUAN Xue-xia.Response surface method based on LS-SVM for structural reliability analysis［J］.Journal of Zhejiang University Engineering Science，2007，41(1):44-47.(in Chinese)金伟良，袁雪霞.基于LS-SVW的结构可靠度响应面分析方法 ［J］.浙江大学学报工学版，2007，41(1):44-47.

［14］ LU Yan，XIE Xue-shu.A multi-dimensional interpolation global optimization algorithm and its application ［J］.Information and Control，1992，21(2):84-89.(in Chinese)吕 彦，解学书.多元插值全局优化算法及其应用［J］.信息与控制，1992，21(2):84-89.

［15］ CHEN Kui.Design and Analysis of Experiments［M］.Beijing:Tsinghua University Press，2005.(in Chinese)陈 魁.实验设计与分析［M］.北京:清华大学出版社，2005.

［16］ LI Sheng-yong，ZHANG Zhe，SHI Lei，et al.A new method for selecting sampling points in response surface method ［J］.Computational Mechanics，2009，24(6):899-903.(in Chinese)李生勇，张 哲，石 磊，等.一种在响应面法中选取样本点的新方法 ［J］.计算力学学报，2009，24(6):899-903.

［17］ GONG Jin-xin.Computation Method for Reliability of Engineering Structure［M］.Dalian:Dalian University of Technology Press，2003.(in Chinese)贡金鑫.工程结构可靠度计算方法［M］.大连:大连理工大学出版社，2003.