畸变缺陷对冷弯薄壁型钢柱力学性能的影响
姚永红,武振宇
1)哈尔滨工业大学土木工程学院,哈尔滨150090;2)安徽理工大学土木建筑学院,安徽淮南232001
冷弯薄壁卷边槽钢柱在制作、运输及安装过程中,不可避免地在构件中产生初始几何缺陷.研究表明,初始几何缺陷对试件的极限承载力和变形有显著影响[1-3].现阶段在数值计算中考虑初始几何缺陷影响的一种方法是:在非线性屈曲分析之前进行特征值屈曲分析,提取一阶屈曲模态作为初始缺陷的分布模式输入模型中,其缺陷值按实测结果输入.冷弯薄壁型钢柱在轴心压力作用下,易发生局部屈曲、畸变屈曲和整体屈曲,包括以上2种或3种屈曲模式耦合在一起的复杂屈曲模式.局部和整体初始缺陷对冷弯薄壁型钢构件承载力的影响已得到较充分认识[1-2,4].近年来,随着高强钢材和腹板加劲构件的使用,使得畸变屈曲可能先于局部屈曲发生[5-9],成为构件失效的控制模式,如图1.
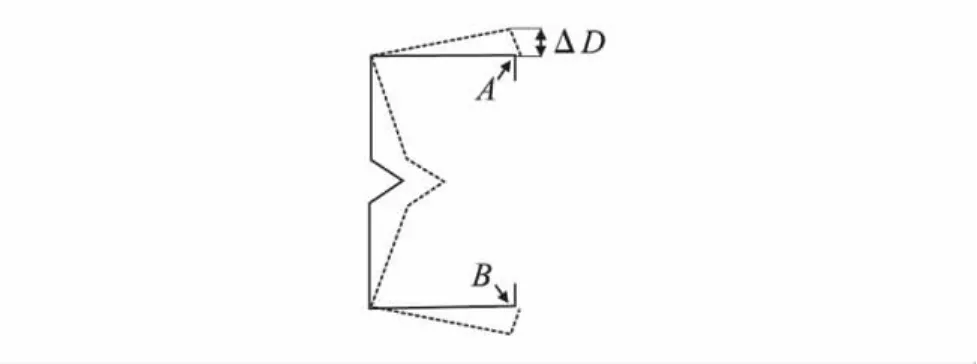
图1 冷弯薄壁型钢轴压构件畸变屈曲变形Fig.1 Distortional buckling deformation of cold-formed thin-walled steel under axial compression
畸变屈曲的破坏机理不同于局部屈曲和整体屈曲,因此畸变缺陷的影响规律尚待进一步研究.目前,由于对冷弯薄壁型钢构件畸变初始缺陷的状态了解不多,试件畸变初始缺陷的大小在分析时较难确定,并且在特定模态中考虑最大缺陷值可能得出非常保守的结果[3].本研究对8个短柱和12个中长柱腹板V形加劲冷弯薄壁型钢柱构件进行了畸变初始缺陷测量,绘出初始缺陷沿试件纵向分布图,列出所测构件畸变缺陷沿试件纵向的平均值和最大值.以此为基础,用数值计算方法分析畸变初始缺陷对试件畸变屈曲承载力及畸变屈曲侧向变形最大值的影响,并给出了此类型冷弯薄壁型钢构件在数值计算时应考虑畸变初始缺陷的建议.
1 畸变缺陷测量
1.1 试件
试件截面形状如图1粗线部分所示,腹板名义宽度H取190 mm和230 mm两种,腹板中间设有V形加劲肋,加劲肋高度S为15 mm,翼缘宽度和卷边宽度分别为75 mm和20 mm,试件实测壁厚t为2.98 mm.本研究所选取的截面在制作之前进行了详细设计,用有限条方法和有限元方法对拟采用的截面进行弹性屈曲分析,为确保柱构件发生畸变屈曲失效,经试算后,短柱和中长柱试件长度分别选取700 mm和1 400 mm.试件两端磨平后焊有厚度10 mm的端板.
为方便区分各试件,测量前对所有待测试件进行了编号,其规则如图2.工程中,为方便管道和电线等设施的穿越[10-14],往往在构件腹板上开有槽形孔洞.为考虑这种情况,本研究部分试件在腹板上开有槽形孔洞,孔洞尺寸及在柱试件中的位置如图3所示,L为柱长.
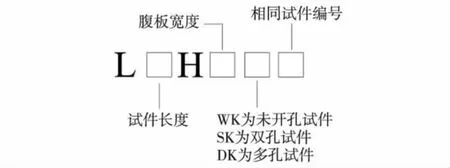
图2 试件编号规则Fig.2 Specimen labeling rule
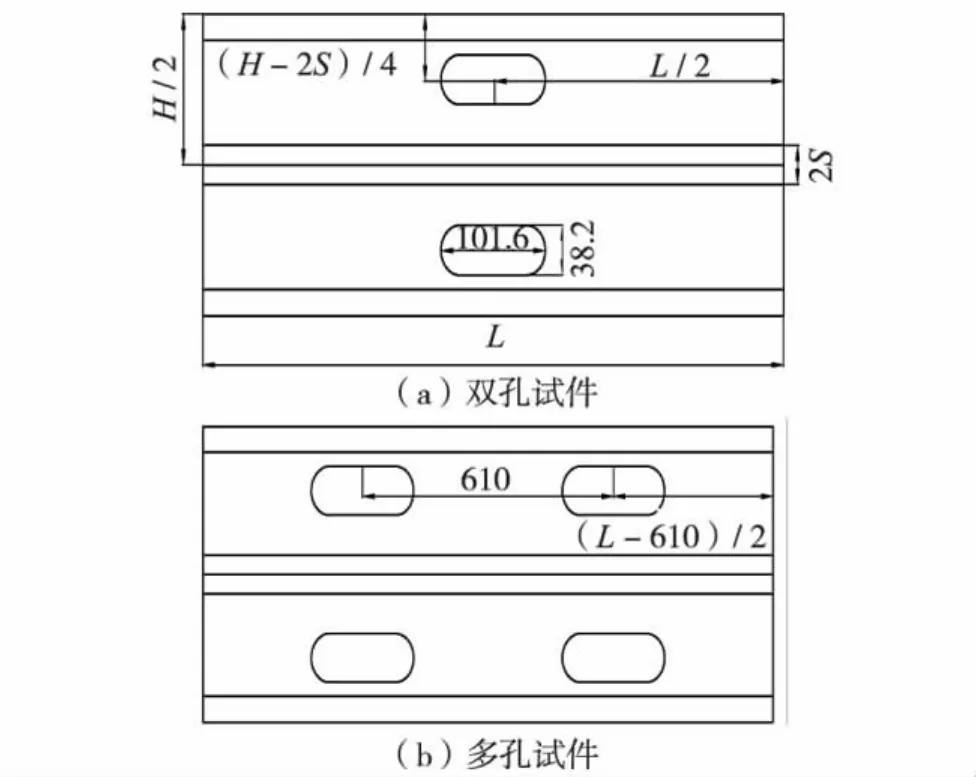
图3 试件孔洞位置 (单位:mm)Fig.3 Hole location in specimen
1.2 测量装置及方法
针对畸变屈曲特点,本研究参照文献 [15-16],采用图4所示测量装置.缺陷测量前,首先沿被测试件纵向划分网格,每隔50 mm布设1个测量截面,每个截面测量卷边和翼缘交接处畸变初始缺陷,如图1中的A点和B点.测量畸变初始缺陷时,先架上刚性杆,读取百分表数值1次,然后去掉刚性杆再读1次,取2次读数的差值,再减去刚性杆上表面至支点下表面间的高度,所得结果即是被测点的缺陷值.规定畸变初始缺陷以外凸为正,内凹为负.由于试件端部均焊有端板,端部截面缺陷未测量.

图4 畸变初始缺陷测量装置Fig.4 The device for measuring initial distortional imperfection
1.3 测量结果
图5为部分试件测得的畸变初始缺陷沿构件纵向分布图.表1列出各试件测得的畸变缺陷最大值和平均值,缺陷最大值 ΔD为 -2.86~2.46 mm,是试件厚度的20% ~96%;平均值Δd为-1.36~2.39 mm,是试件厚度的8% ~88%.
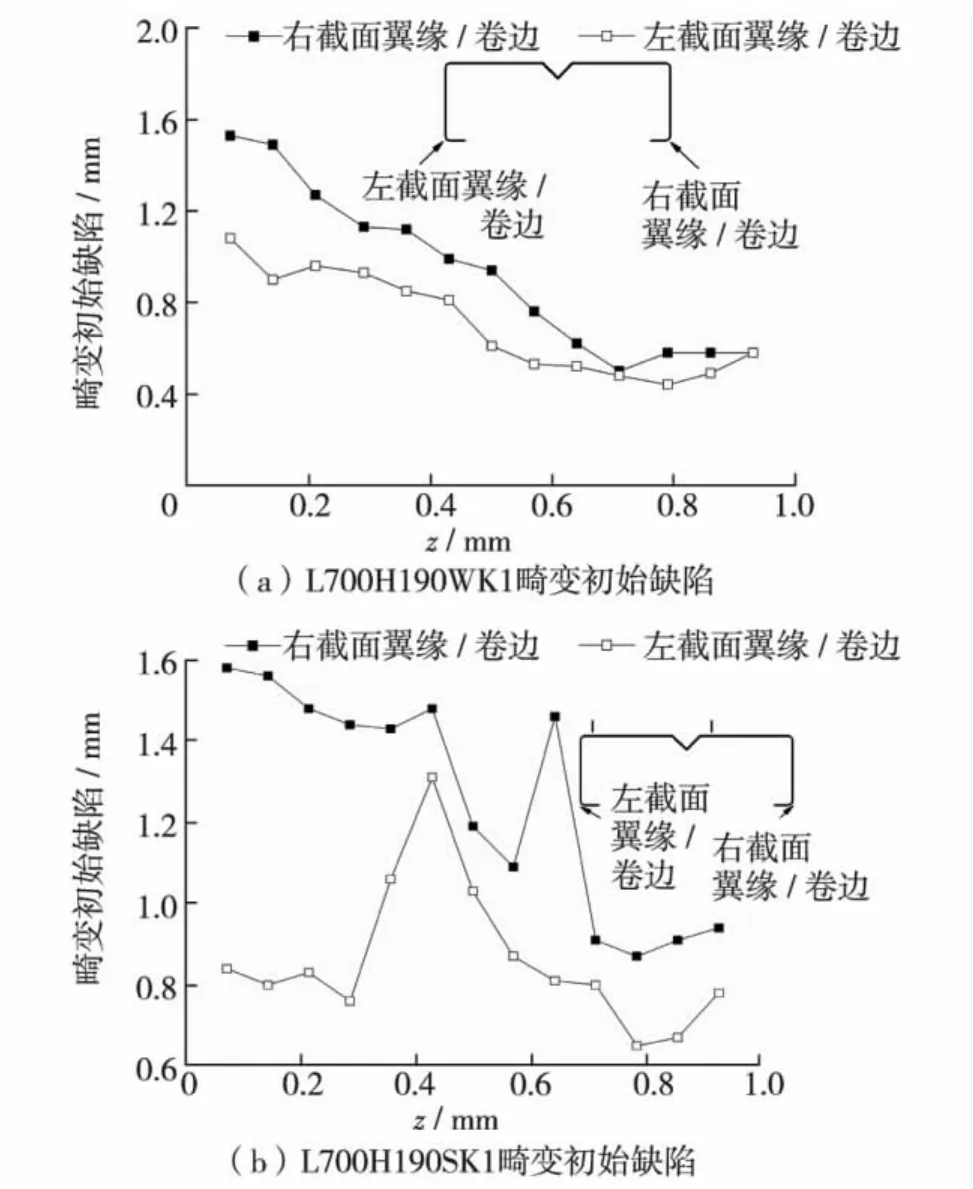
图5 畸变缺陷沿构件纵向分布图Fig.5 Distortional imperfection distribution of specimens

表1 畸变缺陷量测值Table 1 The measured values of distortional imperfection
2 畸变缺陷的影响
畸变缺陷测量结束后,对所有试件进行了轴心受压试验,以获取构件极限承载力和畸变屈曲侧向变形最大值等数据.试验采用50 t四柱试验机作为加载装置,试验方案及加载过程见文献 [17].试验达到了预期效果,所有柱试件均发生畸变屈曲失效,如图6.本研究通过数值分析方法,考虑畸变初始缺陷对试件力学性能的影响,采用大型通用有限元软件ANSYS中的Shell181单元,考虑几何和材料双重非线性,未考虑残余应力和弯角处屈服强度的提高[18-20].建模时模拟了试件焊接端板以及试件卷边和翼缘、翼缘和腹板处弯角的影响.单元网格尺寸对模拟结果有一定影响,经反复验证发现,当网格为10 mm×5 mm时,计算结果可获得较高精度.数值分析时输入的材料属性通过试验测得[17],弹性模量E=203 170 MPa,屈服强度fy=363.00 MPa,泊松比 ν=0.303.

图6 加劲冷弯薄壁卷边槽钢柱构件畸变屈曲失效Fig.6 Cold-formed thin-walled steel stiffened lipped channel column failed from distortional buckling
有限元分析过程为:首先进行特征值屈曲分析,按照“一致缺陷模态法”思路,提取第一阶屈曲模态作为初始缺陷的分布输入下一阶段分析;然后采用弧长法进行非线性屈曲分析,获取构件的失效模式、承载力和畸变屈曲侧向变形最大值.为研究畸变初始缺陷对试件力学性能的影响,输入的缺陷值对应于各个试件在缺陷测量时获得的实测值,其大小分别按所测最大值和沿试件纵向平均值考虑.试件极限承载力以及畸变屈曲侧向变形最大值都是反映试验结果的重要指标,表2列出了有限元数值计算所得结果和试验数据的比较.其中,pt为试验测得的极限承载力;p1和p2分别为有限元分析时,输入畸变初始缺陷最大值和平均值所得的极限承载力;Δt为试验测得极限承载力时对应的畸变屈曲侧向变形最大值;Δ1和Δ2为有限元分析所得极限承载力时畸变屈曲侧向变形最大值,分别由输入畸变初始缺陷最大值和平均值计算得到.p1/pt平均值为0.961,标准差为 0.034;p2/pt平均值为 0.991,标准差为 0.025;Δ1/Δt平均值为 1.259,标准差为0.222;Δ2/Δt平均值为0.995,标准差为 0.063.从表2可见,输入所测畸变缺陷最大值时,极限承载力大部分小于试验值,最大相差10%左右,而畸变屈曲侧向变形最大值普遍大于试验值;当输入畸变缺陷平均值时,极限承载力与试验值非常接近,最大偏差不到6%,畸变屈曲侧向变形最大值也与试验值相差不大.本研究有限元分析输入沿试件纵向畸变初始缺陷平均值所得结果好于输入畸变初始缺陷最大值.无论是输入畸变缺陷平均值还是最大值,数值分析得到的试件失效模式均与试验结果完全相同.这是因为畸变初始缺陷最大值反映的是某个截面的缺陷,单纯考虑该值可能使计算结果偏于保守;而沿构件纵向畸变初始缺陷平均值反映的是整个试件多个截面的缺陷,与现实更接近;柱构件的屈曲失效模式与试件截面尺寸、截面类型、柱长以及钢材材性等因素有关,而缺陷大小只会对极限承载力和变形值产生影响.图7(a)给出试件L1400H190SK2试验以及有限元分析所得极限荷载-侧向畸变变形曲线,图7(b)给出完整的荷载-侧向畸变变形曲线.从图7(a)可见,加载初期有限元分析值与试验曲线吻合不是很好,但加载一段时间后,与考虑平均缺陷所得曲线十分接近,而输入最大缺陷时,曲线偏离较大.
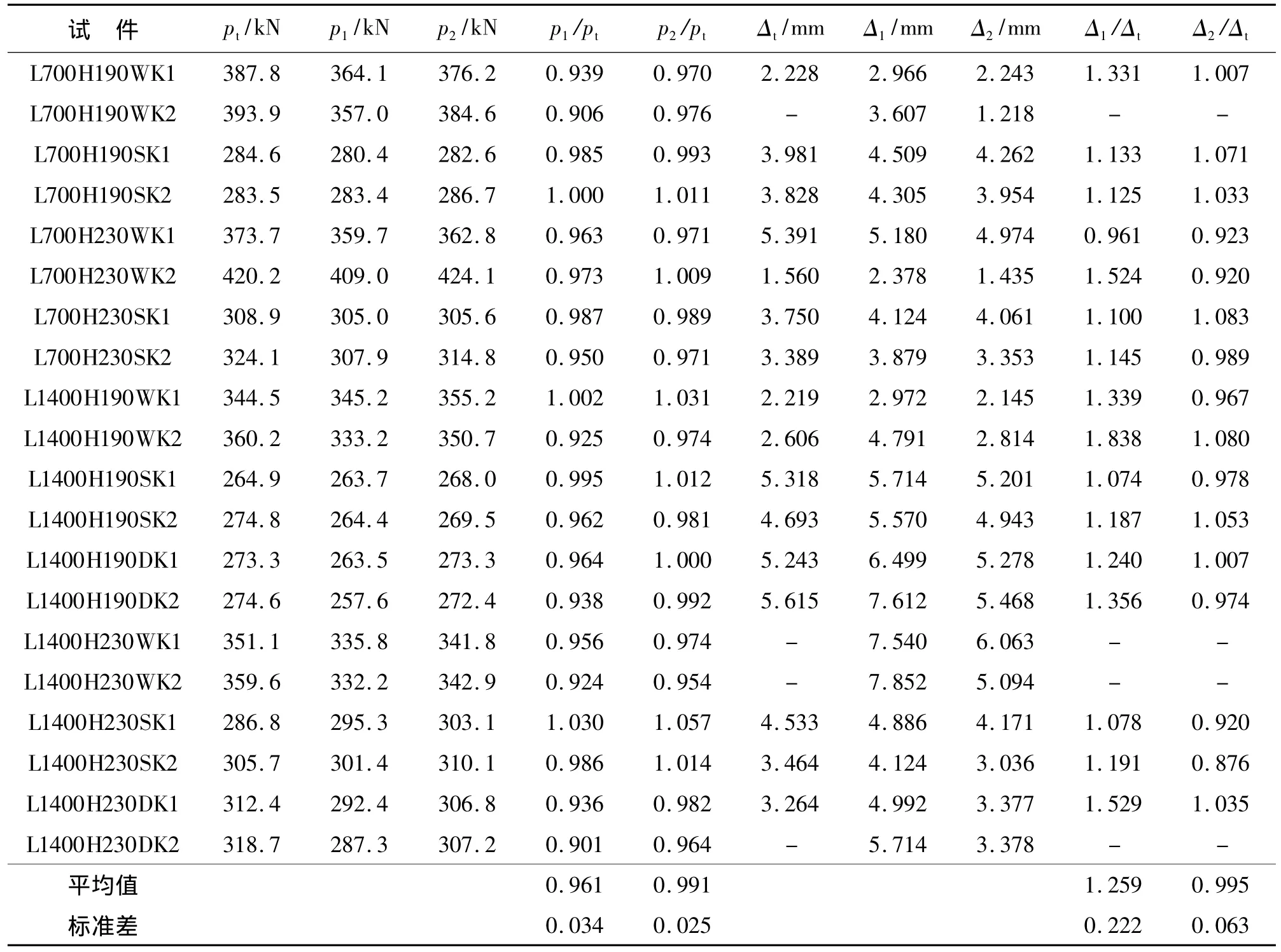
表2 试验和有限元分析数据比较Table 2 Test results contrast to finite element analysis

图7 荷载-侧向畸变变形曲线Fig.7 Load versus lateral distortional deformation curves
3 数值计算建议
畸变初始缺陷对腹板V形加劲冷弯薄壁型钢柱构件力学性能影响较大,在数值模拟时需认真对待.在分析之前,如果对每根试件进行缺陷测量,工作量非常大.为此,在实测资料有限的条件下,能提出在数值模拟时考虑畸变缺陷的方法,将非常有意义.分析表明,输入缺陷值越大,对应的极限承载力越小,如果模拟时输入一个较大的畸变缺陷值,固然会使设计偏于安全,但不利于材料的合理使用.通过前文分析,建议按如下方法考虑畸变缺陷:畸变缺陷沿试件纵向平均值大多数构件只有0.4t ~ 0.6t,最大为0.88t.在考虑充足的安全储备条件下,建议数值计算时,畸变初始缺陷值取构件厚度的 0.90 倍,即 0.90t.
结 语
对20个腹板V形加劲冷弯薄壁卷边槽钢柱试件进行了畸变初始缺陷的测量以及轴心受压试验研究,经与有限元模拟结果分析对比可知:① 本次测量所得畸变初始缺陷最大值是试件厚度的20%~96%,沿试件纵向平均值是试件厚度的8%~88%;②对所有试件进行了有限元模拟,考虑了2种不同畸变初始缺陷值的影响.与试验结果对比分析发现:畸变初始缺陷的大小不会改变试件的失效模式;输入的畸变初始缺陷值越大,计算得到的极限承载力越低,而畸变屈曲侧向变形最大值越大;输入最大缺陷时,所得计算值较保守,而输入沿试件纵向缺陷平均值时,所得计算结果与试验数据吻合较好;③根据本文分析结果,腹板V形加劲冷弯薄壁卷边槽钢柱构件进行数值模拟时,建议畸变初始缺陷选取0.90倍试件壁厚.
/References:
[1] WANG Chun-gang.Stability Behavior Analysis and Experimental Study on Singly-symmetric Cold-formed Thinwalled Steel Members Under Compression Loading[D].Harbin:Harbin Institute of Technology,2007.(in Chinese)王春刚.单轴对称冷弯薄壁型钢受压构件稳定性能分析与试验研究 [D].哈尔滨:哈尔滨工业大学,2007.
[2] CHEN Ji.Stability of Steel Structures Theory and Design[M].Beijing:Science Press,2006.(in Chinese)陈 骥.钢结构稳定理论与设计 [M].北京:科学出版社,2006.
[3] Schafer B W,Peköz T B.Computational modeling of coldformed steel:characterizing geometric imperfections and residual stresses[J].Journal of Constructional Steel Research,1998,47(3):193-210.
[4] FU Xue-yi,WU Bing,CHEN Xian-chuan,et al.The structural design of a tall building in Qatar[J].Journal of Shenzhen University Science and Engineering,2007,24(1):1-8.(in Chinese)傅学怡,吴 兵,陈贤川,等.卡塔尔某超高层建筑结构设计[J].深圳大学学报理工版,2007,24(1):1-8.
[5] Yap D C Y,Hancock G J.Experimental study of highstrength cold-formed stiffened-web C-sections in compression [J].Journal of Structural Engineering,2011,137(2):162-172.
[6] Kwon Y B,Kim B S,Hancock G J.Compression tests of high strength cold-formed steel channels with buckling interaction [J].Journal of Constructional Steel Research,2009,65(2):278-289.
[7] Yang D M,Hancock G J.Compression tests of high strength steel channel columns with interaction between local and distortional buckling[J].Journal of Structural Engineering,2004,130(12):1954-1963.
[8] YAO Xing-you,LI Yuan-qi,SHEN Zu-yan.Distortional buckling behavior of high-strength cold-formed thin-walled steel lipped channel columns under axial compression[J].Journal of Building Structures,2010,31(11):1-9.(in Chinese)姚行友,李元齐,沈祖炎.高强冷弯薄壁型钢卷边槽形截面轴压构件畸变屈曲性能研究 [J].建筑结构学报,2010,31(11):1-9.
[9] Chen J,He Y,Jin W L.Stub column tests of thin-walled complex section with intermediate stiffeners[J].Thin-Walled Structures,2010,48(6):423-429.
[10] Moen C D,Schafer B W.Experiments on cold-formed steel columns with holes [J].Thin-Walled Structures,2008,46(10):1164-1182.
[11] Moen C D,Schafer B W.Direct strength method for design of cold-formed steel columns with holes[J].Journal of Structural Engineering,2011,137(5):559-570.
[12] Moen C D,Schafer B W.Direct strength design of coldformed steel members with perforations[R].Washington:American Iron and Steel Institute,2009.
[13] Yu C.Cold-formed steel flexural member with edge stiffened holes:behavior,optimization,and design [J].Journal of Constructional Steel Research,2012,71(4):210-218.
[14] HU Bai-xiang,LIU Yong-juan.Ultimate load capacity of cold-formed lipped channel member with web perforation subjected to axial compression [J].Journal of Jiangsu U-niversity:Natural Science Edition,2007,28(3):258-261.(in Chinese)胡白香,刘永娟.轴压单孔冷弯薄壁槽形中长钢柱的极限承载力 [J].江苏大学学报:自然科学版,2007,28(3):258-261.
[15] WANG Chun-gang,ZHANG Yao-chun,ZHANG Zhuangnan.Experimental investigation on channel columns with inclined simple edge stiffeners under compression loading[J].Journal of Building Structures,2006,27(3):1-9.(in Chinese)王春刚,张耀春,张壮南.冷弯薄壁斜卷边槽钢受压构件的承载力试验研究 [J].建筑结构学报,2006,27(3):1-9.
[16] ZHOU Xu-hong,WANG Shi-ji.Stability of Thin-walled Structures Theory and Application[M].Beijing:Science Press,2009.(in Chinese)周绪红,王世纪.薄壁构件稳定理论及其应用 [M].北京:科学出版社,2009.
[17] YAO Yong-hong,WU Zhen-yu,CHENG Bo,et al.Experimental investigation into axial compressive behavior of cold-formed thin-walled steel columns with lipped channel and openings[J].Journal of South China University of Technology:Natural Science Edition,2011,39(9):61-67.(in Chinese)姚永红,武振宇,成 博,等.开孔冷弯薄壁卷边槽钢柱轴压性能的试验研究 [J].华南理工大学学报:自然科学版,2011,39(9):61-67.
[18] Dubina D,Ungureanu V.Effect of imperfections on numerical simulation of instability behaviour of cold-formed steel members [J].Thin-Walled Structures,2002,40(3):239-262.
[19] Abdel-Rahman N,Sivakumaran K S.Material properties models for analysis of cold-formed steel members [J].Journal of Structural Engineering,1997,123(9):1135-1143.
[20] Schafer B W,Li Z,Moen C D.Computational modeling of cold-formed steel[J].Thin-Walled Structures,2010,48(10-11):752-762.

