大跨度桥梁各态历经脉动风场的数值模拟分析

郑恒斌，颜全胜，2，王卫锋，2，吴 杰

1)华南理工大学土木与交通学院，广州510640;2)华南理工大学亚热带建筑科学国家重点实验室，广州510640

在实际大气边界层湍流中，脉动风速不仅是时间函数，且随空间位置(x，y，z)变化，是一个单变量四维随机场［1］.通常情况下，当不考虑x、y、z方向的风速互相关时，可将脉动风场看成一个一维多变量的随机向量过程［2］.对于随机风场的模拟方法许多学者都进行了研究，其中由Rice提出并经Shinozuka等［3-4］发展的基于原型谱表示的谐波合成法，因具有适用范围广、精度高等优点，成为脉动风场最主要的模拟方法，代表了脉动风场随机模拟的主流方向.对传统的谐波合成方法，不少学者也对其计算效率不高，占用计算机资源较大进行了改进［2，5-13］.其中由 Chen［8］较早采用并由胡亮等［9-13］发展并不断完善的基于本征正交分解 (proper orthogonal decomposition，POD)的谱表示法是近年研究热点.

本研究采用该法进行脉动风场的模拟，其模拟思路为在功率谱矩阵的分解中通过POD法代替传统的Cholesky分解法，结合模态截断技术在满足计算精度和随机过程统计特性的前提下，用少数能量较大的低阶“风吹动模态”［14］的线性组合来近似表达整个随机过程，因此相对其他以Cholesky分解法为核心算法的模拟方法而言，可大大提高计算效率.根据分解对象的不同，该法可以分为基于相干函数矩阵的POD型谱表示法［9］和基于互功率谱密度矩阵的POD型谱表示法［10］，前者通过引入双索引频率，实现了各态历经脉动风场的模拟［11］，后者尚不具备各态历经性，不便于应用，尚需拓展完善.本研究以脉动风场POD型谱表示法为基础，根据桥梁主梁处脉动风场的特点，对互功率谱密度矩阵进行简化，推导了大跨度桥梁主梁脉动风场模拟的实值简化公式，引入双索引频率和快速傅里叶变换 (fast Fourier transform，FFT)加速算法，编制了相应的FORTRAN程序，实现了大跨度桥梁主梁处基于互谱密度矩阵POD型谱表示法的各态历经脉动风场的快速模拟.本方法同样适用于大跨度桥梁三维脉动风场的模拟.

1 脉动风场模拟简化公式

将需要模拟的脉动风场近似看成为零均值、平稳的一维 n变量随机向量过程，即 V0(t)=［v01(t)，v02(t)，…，v0n(t)］T，其中 v0j(t)(j－ 1，…，n)表示各分量过程，上标“0”表示需要模拟的目标值，其互谱密度矩阵可表示为

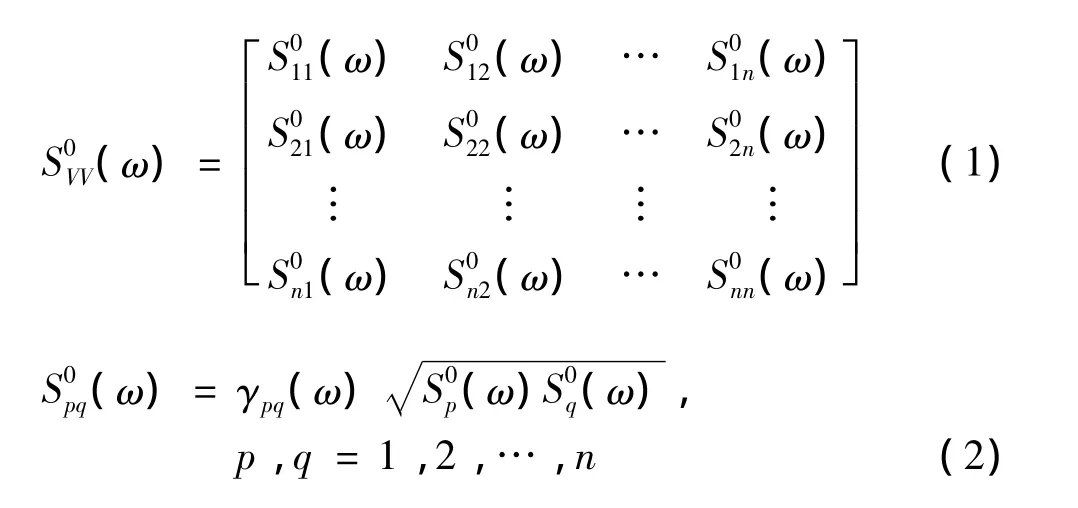
其中，S0p(ω)和S0q(ω)分别为各分量过程的自功率谱密度(假设为双边谱);γpq(ω)为变量之间的相干函数.一般情况下，大跨度桥梁位置所处的地表状态基本不变，地表起伏较小，桥面的高差也较小.针对这一条件，将桥面脉动风场模拟的各点近似认为处于同一高度和相同的地表状态参数下，从而具有相同的自功率谱密度函数值，即式 (1)中S011(ω)=S022(ω)= … =S0nn(ω)=S0(ω).因此，式(1)可简化为

实际工程中，脉动风的功率谱密度值和空间各点的相关函数值均为实数，因此式(3)是一个实数域的对称矩阵，且经证明为半正定的Hermite矩阵［15］.通过采用矩阵的正交分解法可得到n个互异的特征值η1(ω)≥η2(ω)≥…≥ηn(ω)，对应的特征向量φ1(ω)，φ2(ω)，…，φn(ω)全为实数.对特征值和特征向量进行正交化处理后，原功率谱密度矩阵可展开为

引入模态截断技术后，式 (4)可进一步近似为

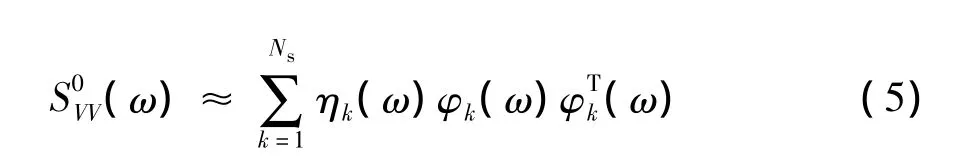
其中，Ns为POD的模态截断阶数，且Ns≪n，其值需要通过误差分析得到.根据推导［4，10］，可得到脉动风场基于互谱密度矩阵的POD型谱表示法的模拟公式为

其中，Vj(t)为j点处t时刻的脉动风速;φj，k(ωl)为第k阶特征向量的第j行元素值;M为频率分割数;Δω =(ωup－ω0)/M为频率步长，ωup和ω0分别为需要模拟的上下限截止频率;ωl=l×Δω;θ(k)l为独立在［0，2π］区间的均匀分布的随机相位角.本研究采用以能量评判准则为基础的精确公式进行计算，推导得到的误差分析表达式为

其中，ε为截断误差，在综合考虑计算效率和精度的前提下根据需要取值.

2 各态历经性参数的引进

类似文献 ［4］，将双索引频率引入到式 (6)中，可推导得到基于互谱密度矩阵的POD型谱表示法的各态历经随机风场模拟公式为

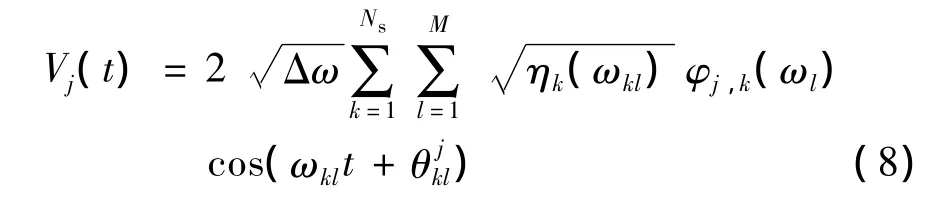
3 FFT技术对算法的加速

同其他基于谱表示的谐波合成法一样，式 (8)可采用FFT进行加速，从而大大提高计算效率，且可改写为［4，11］

其中，p=1，2，…，TNUM，TNUM为需要模拟的总时间步数;Δt为时间间隔;q=mod(p，NT)，NT为DFT变换点数;Gjk(qΔt)可通过引入FFT算法得到，

其中，q=1，2，…，NT

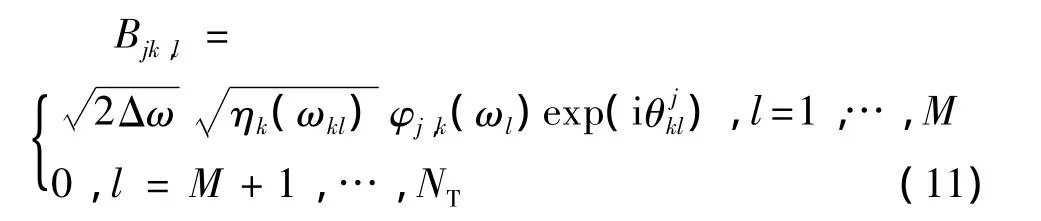
在引入FFT技术后，时间间隔Δt为

根据FFT变换的需要，式 (12)中频率分割点总数M和采样点总数NT均为2的整数次幂值.根据采样定律，为避免频域混叠和模拟时程曲线失真，Δt还需要满足将此条件代入式(12)，可得到确定M和NT的关系式为

4 数值算例分析

以某城际轨道交通工程中的一座特大桥为算例，运用本文方法，对该桥主梁水平脉动风场进行模拟.该桥跨布置为 (108.85+185×2+115.5)m预应力混凝土连续刚构桥，为迄今世界上最大主跨的无碴轨道刚构铁路桥，全长595.75 m，其结构布置如图1.

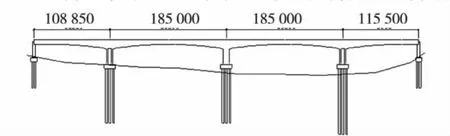
图1 某特大桥跨径布置图 (单位:mm)Fig.1 Span arrangement of the long-span bridge

该桥主梁脉动风速模拟点布置在桥面上，并沿跨长方向等距分布间距为10 m，全桥模拟点Nsum=59.脉动风速目标功率谱采用能够考虑高度变化影响的 Kaimal功率谱［4，16］，其表达式为

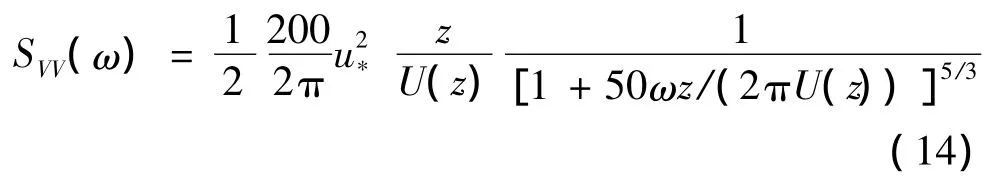
其中，ω∈［0，2π］;z为模拟点相对于基准点的高度，U(z)为高度z处的平均风速，可通过梯度风的指数型分布［16］换算得到.按100年重现期标准，经换算后桥面处U(z)=36.5 m/s，u*为气流的剪切摩阻速度，取u*=3.68 m/s.相干函数采用Davenport［17］表达式

表1 主梁脉动风场模拟的部分参数表Table 1 Partial parameters of the simulated fluctuating wind field

图2 特征值截断阶数Ns与对应的计算精度趋势图Fig.2 Calculation accuracy trend corresponding to truncation order number of eigenvalue

图3和图4分别为按照本方法模拟的两主跨跨中附近点21和点40前1 000 s的脉动风速时程曲线，两点之间相距190 m.在Matlab中对模拟风场的前4 096 s采用Welch法进行功率谱估计，分别得到的点21估计的自功率谱与目标谱的对比图(见图5)，以及点21和40两点间互功率谱与目标谱的对比图 (见图6).从图5和图6可看出，无论是自谱或互谱，模拟得到的估计谱与目标谱之间误差均较小且吻合良好，从而验证了本文方法的正确性和有效性.

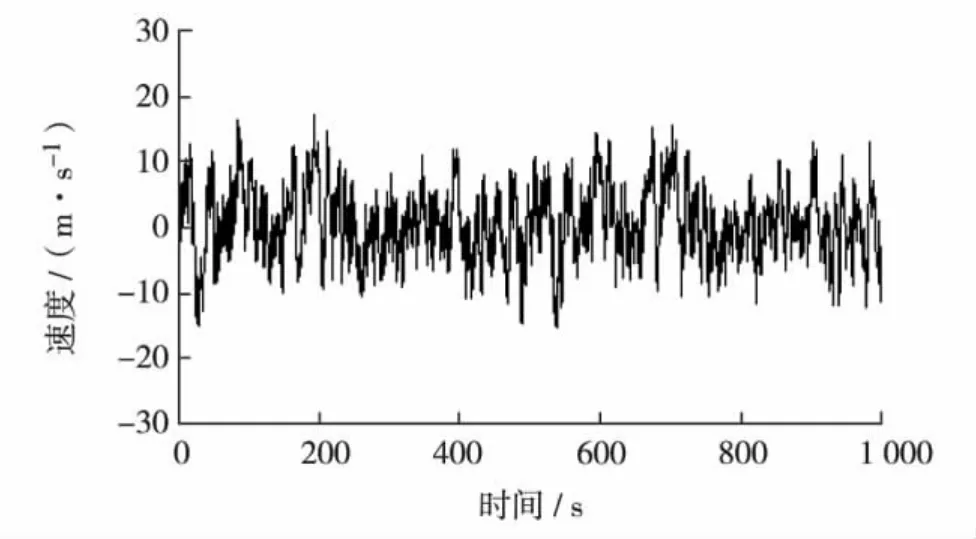
图3 主跨跨中附近点21脉动风速时域曲线图Fig.3 Time histories of simulated turbulence wind velocity of 21st point near main mid-span

图4 主跨跨中附近点40脉动风速时域曲线图Fig.4 Time histories of simulated turbulence wind velocity of 40th point near main mid-span

图5 点40的自谱密度检验图Fig.5 Auto power spectrum test pattern of 40th point

图6 点21和点40互谱密度检验图Fig.6 Cross-power spectral density of point 21 and 40 test pattern

另外，针对上述算例中主要计算过程的耗时量进行统计，其中矩阵正交分解时间约占据总计算时长的43.1%，基于FFT变换的风场合成时间约占据总计算时长的26.3%，由此可知，类似于Deodatis方法［4］中的Cholesky分解，矩阵的正交分解是整个模拟过程主要的耗时步骤，并随着模拟点数的增多、互谱密度矩阵维数的增大和模拟各态历经风场频率分割数的增加，分解机时也将随之提高，因此矩阵正交分解速度是本研究方法中控制风场合成效率的关键.

图7为矩阵Jacobi变换法和隐式QL法应用在本研究算例中随截断阶数的不同而得到的互谱密度矩阵分解时长对比图.从图7可见，无论哪种分解方法，分解时长都随着截断阶数的增加而线性增大，而隐式QL法相对Jacobi变换法而言具有很高的计算效率，前者的计算速度大约为后者的10倍，因此在本研究的分解计算中采用隐式QL法.研究表明，采用合适的分解方法可以大幅提高计算效率，从而使本研究方法成为具有竞争力的模拟方法.

图7 两种正交分解法随截断阶数变化的矩阵分解时长图Fig.7 The matrix decomposition duration time of different methods corresponding with truncation order number changed

结 语

综上可知，① 通过比较互功率谱密度矩阵正交分解的截断阶数与计算精度，进一步说明了随机过程本征正交分解法采用类似于模态综合法中截断技术的正确性;② 基于本研究方法模拟的脉动风场其估计自功率谱和互功率谱均与目标谱吻合良好，验证了本方法的可行可靠;③ 基于本方法的风场合成效率关键在于矩阵正交分解速度，选用适宜的高效分解方法将大大提高风场合成效率.

/References:

［1］ ZHANG Xi-qian，GE Yong，YAN Chun-feng，et al.The research and development of fluctuating wind field simula-tion technology［J］.Earthquake Engineering and Engineering Vibration，2008，28(6):206-211.(in Chinese)张希黔，葛 勇，严春风，等.脉动风场模拟技术的研究与进展 ［J］.地震工程与工程振动，2008，28(6):206-211.

［2］ CAO Ying-hong，XIANG Hai-fan，ZHOU Ying.Random simulation of wind turbulence field for a long-span bridge［J］.China Civil Engineering Journal，1998，31(3):72-79.(in Chinese)曹映泓，项海帆，周 颖.大跨度桥梁随机风场的模拟 ［J］.土木工程学报，1998，31(3):72-79.

［3］ Shinozuka M，Deodatis G.Simulation of stochastic processes by spectral representation［J］.Applied Mechanics Reviews，1991，44(4):191-203.

［4］ Deodatis G.Simulation of ergodic multivariate stochastic processes ［J］.Journal of Engineering Mechanics，1996，122(8):778.

［5］ DING Shun-quan，CHEN Ai-rong，XIANG Hai-fan.Simulation of spatial fluctuating wind field on long span bridges［J］.Chinese Quarterly of Mechanics，2006，27(2):184-189.(in Chinese)丁顺泉，陈艾荣，项海帆.大跨度桥梁空间脉动风场的计算机模拟 ［J］.力学季刊，2006，27(2):184-189.

［6］ LUO Jun-jie，HAN Da-jian.A fast simulation method of stochastic wind fileld for long-span structures［J］.Engineering Mechanics，2008，25(3):96-101.(in Chinese)罗俊杰，韩大建.大跨度结构随机脉动风场的快速模拟方法 ［J］.工程力学，2008，25(3):96-101.

［7］ LUO Jun-jie，HAN Da-jian.Simulation method for 3-D stochastic wind field around long-span structures ［J］.Journal of Vibration and Shock，2008，27(3):87-91.(in Chinese)罗俊杰，韩大建.大跨度结构三维随机脉动风场的模拟方法 ［J］.振动与冲击，2008，27(3):87-91.

［8］ Chen X，Kareem A.Proper orthogonal decompositionbased modeling，analysis，and simulation of dynamic wind load effects on structures［J］.Journal of Engineering Mechanics，2005，131(4):325-339.

［9］ Hu Liang，Li Li，Fan Jian，et al.Coherency matrix-based proper orthogonal decomposition with application to wind field simulation ［J］.Earthquake Engineering and Engineering Vibration，2006，5(2):267-272.

［10］ HU Liang，LI Li，FAN Jian.Digital simulation of bridge wind fields based on spectral representation method with proper orthogonal［J］.Journal of Wuhan University of Technology Transportation Science and Engineering，2008，32(1):16-19.(in Chinese)胡 亮，李 黎，樊 剑.基于特征正交分解的桥梁风场模拟 ［J］.武汉理工大学学报交通科学与工程版，2008，32(1):16-19.

［11］ HU Liang，LI Li，FAN Jian，et al.Simulation of ergodic wind field using proper orthogonal decomposition-based spectral representation method［J］.Journal of Vibration Engineering，2008，21(2):185-190.(in Chinese)胡 亮，李 黎，樊 剑，等.用特征正交分解对各态历经风场的模拟研究 ［J］.振动工程学报，2008，21(2):185-190.

［12］ LI Li，HU Liang，FAN Jian，et al.Wind field simulation for bridges with wind passage effects by using spectral representation method based on proper orthogonal decomposition(POD)［J］.Journal of Vibration and Shock，2007，26(5):14-18.(in Chinese)李 黎，胡 亮，樊 剑，等.具有桥塔风效应的桥梁风场数值模拟 ［J］.振动与冲击，2007，26(5):14-18.

［13］ HU Liang，GU Ming，LI Li.Errors produced with proper orthogonal decomposition-based spectral representation method in wind velocity field simulation ［J］.Journal of Vibration and Shock，2011，30(4):12-20.(in Chinese)胡 亮，顾 明，李 黎.基于本征正交分解的谱表示法模拟风场的误差 ［J］.振动与冲击，2011，30(4):12-20.

［14］ Di Paola M.Digital simulation of wind field velocity［J］.Journal of Wind Engineering and Industrial Aerodynamics，1998，74-76(1):91-109.

［15］ ZOU Xiao-jiang.Wind Induced Vibration Analysis in Time Domain and Aerostatic Stability Study for Cable-stayed Bridge［D］.Guangzhou:South China University and Technology，2003:26-27.(in Chinese)邹小江.斜拉桥风振响应时域分析及静风稳定性研究［D］.广州:华南理工大学，2003:26-27.

［16］ JTG/T D60-O1-2004.Wind-resistant Design Code for Highway Bridges［S］.(in Chinese)JTG/T D60-O1-2004.公路桥梁抗风设计规范 ［S］.

［17］ Simu E，Scanlan R H.Wind Effects on Structures［M］.New York:John Wiley＆ Sons，1986.