主线机动容量合理分配的匝道协同控制

李 健，贾元华，敖谷昌

1)北京交通大学交通运输学院，北京100044;2)乔治亚大学富兰克林理学院，雅典城30602，美国;3)北京市轨道交通指挥中心，北京100101

通过匝道控制预防与疏导大城市高速公路联络线和快速路拥堵有较好功效［1-3］，其中，主线关联多匝道协同形式最为突出.目前对其相关智能算法［4-5］及控制参数［6-8］的关注较多，而对深入的控制机制和策略［1，8-11］研究则相对欠缺.交通流密度保持在谐动流相位内，且小于同步流最小密度时，道路适度拥挤但通行能力提高［12］.为表征这种通行能力，本文定义“机动容量”概念，即由主线密度、可接受间隙等因素决定的总允许调节量，其分配以效率提升和公平分配为原则.为讨论其利用的方法及作用，本文对主线和匝道进行系统描述，采用一种新的匝道冗余等待时间［13］为关键控制参数，设计“机动容量”均衡分配最优控制方法，并进行案例仿真验证.

1 系统模型描述

考察一段包含n个区间的路段，描述如下.

以ω表示路段各区间的车道数数组，ωi为第i区间车道数，ω = ［ω1，ω2，…，ωi，…，ωn］T.

以δ表示路段各区间的长度数组，δi为第i区间长度，δ= ［δ1，δ2，…，δi，…，δn］T.

以a表示路段各区间容量数组，ai=ωiδi，a=［a1，a2，…，ai，…，an］T= ［ω1δ1，ω1δ2，…，ωiδi，…，ωnδn］T.

由于速度可认为是关于密度的函数，而流量是随机量，不属可控范围，因此仅以密度代表主线状态向量 xM(k)= ［ρ1(k)，ρ2(k)，…，ρi(k)，…，ρn(k)］T.

以xE(k)表示以排队长度代表的入口匝道状态向量，xE(k)= ［ζ1(k)，ζ2(k)，…，ζi(k)，…，ζn(k)］T，ζi(k+1)= ζi(k)+T［di(k)－ ri(k)］，di(k)+ ζi(k － 1)/T ≥ ri(k)≥ ri－min.

以TM(k)表示主线车辆的行驶时间向量，TM(k)=T∑axM(k);以TE(k)表示入口匝道车辆的等待时间向量，c表示为在形式上与a对称而引入的一个单位向量，且TE(k)=T∑cxE(k).

以To(k)表示系统的时间目标向量，To(k)=TM(k)+TE(k)=T∑axM(k)+T∑cxE(k);To(k)是系统总消耗时间的原始形式.

以u(k)表示入口匝道的控制律向量，u(k)=［r1(k)，r2(k)，…，ri(k)，…，rn(k)］T.

以umin表示入口匝道控制律下限约束向量，umin(k)= ［r1－min，r2－min，…，ri－min，…，ρn－min］T.

以wM(k)表示主线的始终端区间和出口匝道驶离产生的扰动变量向量，wM(k)=［q0(k)，s1(k)，s2(k)，…，si(k)，…，sn(k)，qs(k)］T.

以wE(k)表示入口匝道需求产生的扰动变量向量，wE(k)= ［d1(k)，d2(k)，…，di(k)，…，dn(k)］T;后续将以d(k)代表wM(k)和wE(k)表示系统总的扰动变量向量.

主线状态函数xM(k+1)可以表示为xM(k+1)= φ［xM(k)，u(k)，wM(k)］.

入口匝道状态函数xE(k+1)可以表示为xE(k+1)=xE(k)+T·［wE(k)－ u(k)］= φE［xE(k)，u(k)，wE(k)］;系统状态向量可表示为x(k+1)=F(k)［x(k)，u(k)，(k)］.

控制律约束向量形式为CM［x(k)，(k)］≤u(k)≤CE［x(k)，(k)］，有CM［x(k)，(k)］=umin，以及CE［x(k)，(k)］=wE(k)+xE(k)/T.

2 最优控制方法

多匝道协同控制目标方程可表示为

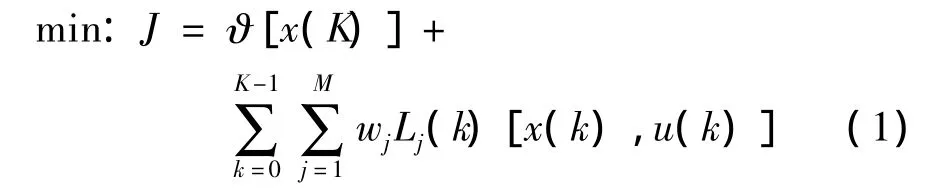
其中，K为时间域;ϑ为终态状态函数;Lj(k)为子系统目标函数;wj为子目标权重;M为子目标数.

采用各匝道调节量与排队长度比值的偏差，即调节率偏差作为控制目标，表示机动容量在满足各匝道需求中资源分配的公平性.

首先，根据控制律向量和匝道状态向量设计一个参数σ，表示匝道调节率向量，

各匝道调节率偏差向量可表示为

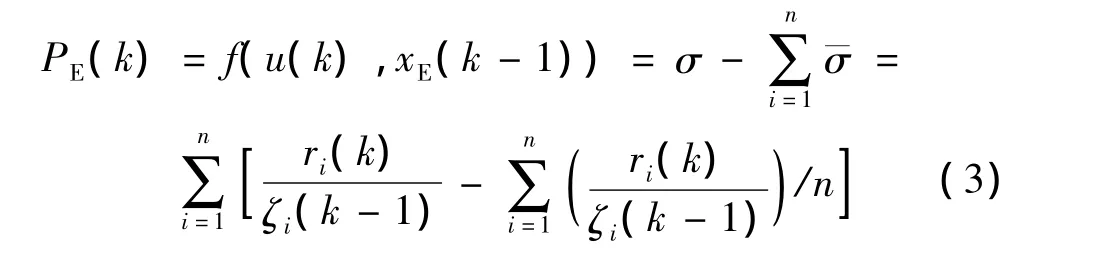
系统控制目标方程为

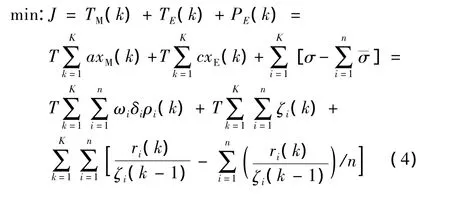
式(4)中，尽管在目标方程中加入了匝道调节率偏差，但反映的信息量很小，因此可省略.则原控制目标方程式(4)可简化为

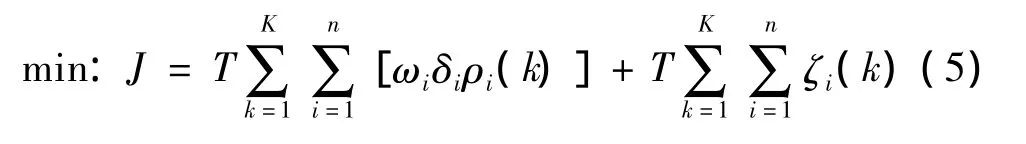
将常量T略去，得

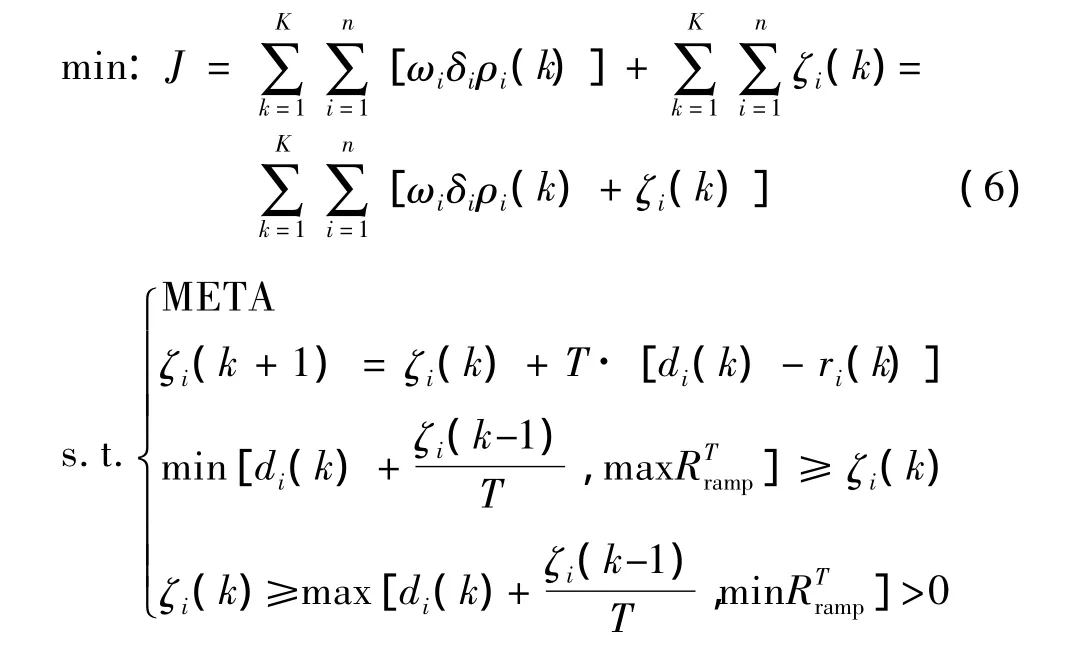
划分区间后ω和δ均可确定，状态参数仅有ρi(k)和ζi(k)为变量，而排队长度ζi(k+1)，其中包含扰动变量和控制变量，求解采用可行方向法［14］.

3 案例仿真与分析

3.1 研究对象

如图1，选择G2联络线下行主线及关联多匝道为研究对象.实地交通流数据取自北京城市道路微波检测系统，包括流量 (含长车流量)、占有率和速度，采样间隔为2 min，交通流关键参数如自由流速度和阻塞密度等［15］参考相关研究辨识.

本文采用最优化方法进行多匝道协同控制对比，并以Matlab仿真实现.

3.2 排队队列对比

对G2下行RS3uG2d、RS4uG2d及RE4dG2d等3个入口匝道在无控制 (N)和协同控制 (C)两种状态下的排队长度进行比较，如图2.

图1 研究对象示意图Fig.1 Illustration of research ramp and mainline

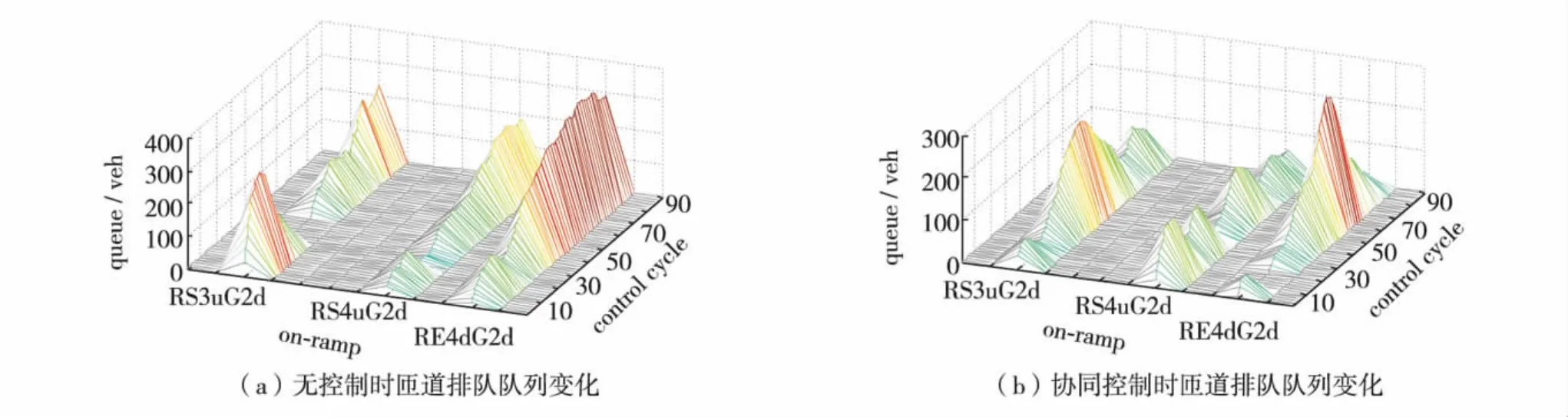
图2 主线关联多匝道排队长度对比 (2 min)Fig.2 Ramp queue profile comparison(2 min)

RS3uG2d、RS4uG2d及 RS4uG2d长度分别为290、650及900 m，容量约为40、85及120 pcu，采用容量负担比bi(k)表示队列长度与匝道容量之比，如图3.无控制时均有明显排队溢出.实施协同控制后，bi(k)值总体降低，但排队溢出仍突显.实际中，即使在高峰期，匝道排队超过容量2～5倍的现象也很难出现.因此，需进一步分析修正.

原因分析及改进方法:在排队溢出影响主线引起拥堵时，可将主线拥堵车辆视为匝道排队，由于存在替代路径，排队一般不会持续增加;控制周期为2 min，按交通流整体推进速度为60～70 km/h计算，区间长度约为2 000～2 200 m，按照离散化路段考虑，很多机动容量未利用.如果控制周期更长，排队长度还会继续增加，与实际情况差距更大.因此，以800～1 000 m汇入区间考虑，交通流整体推进速度仍按60～70 km/h计算，设定控制周期为40 s，对两种场景重新仿真，如图4.

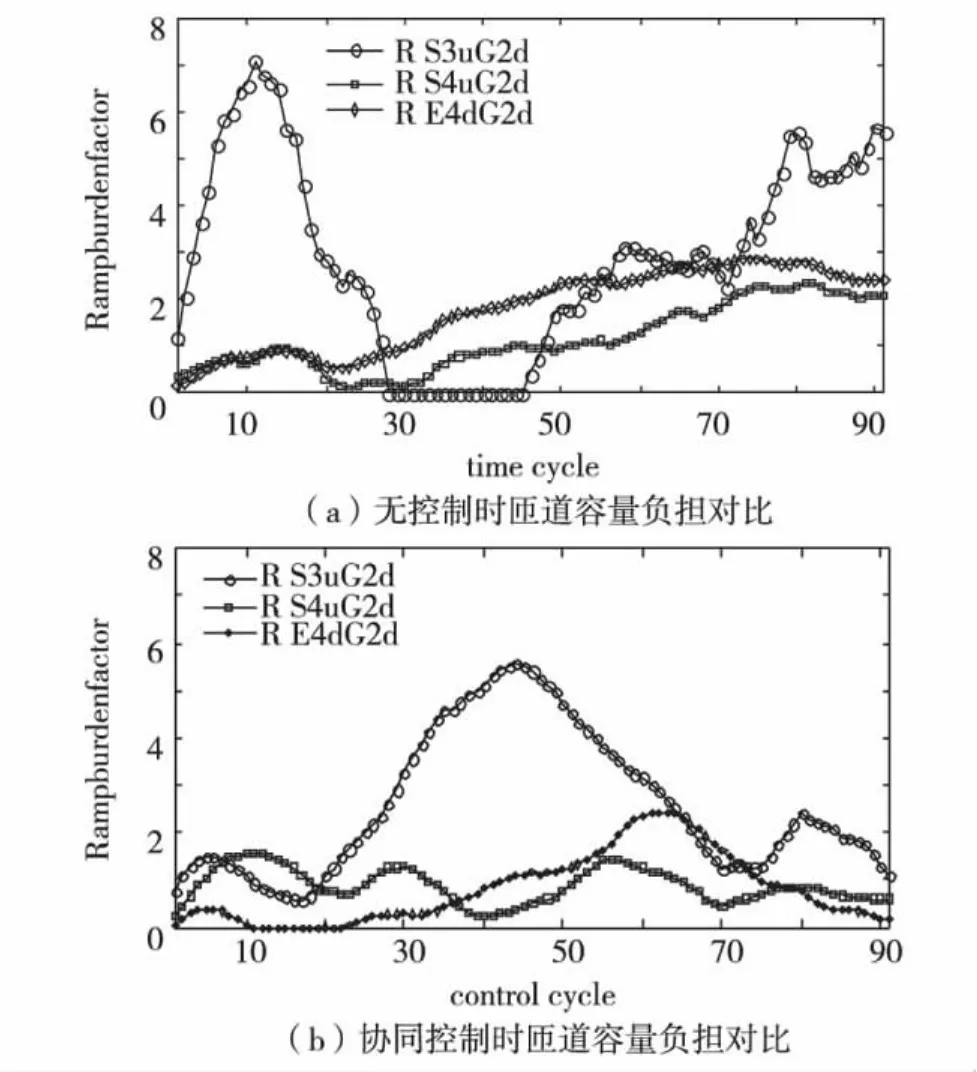
图3 主线关联多匝道容量负担对比 (2 min)Fig.3 Ramp queue and capacity comparison profile(2 min)

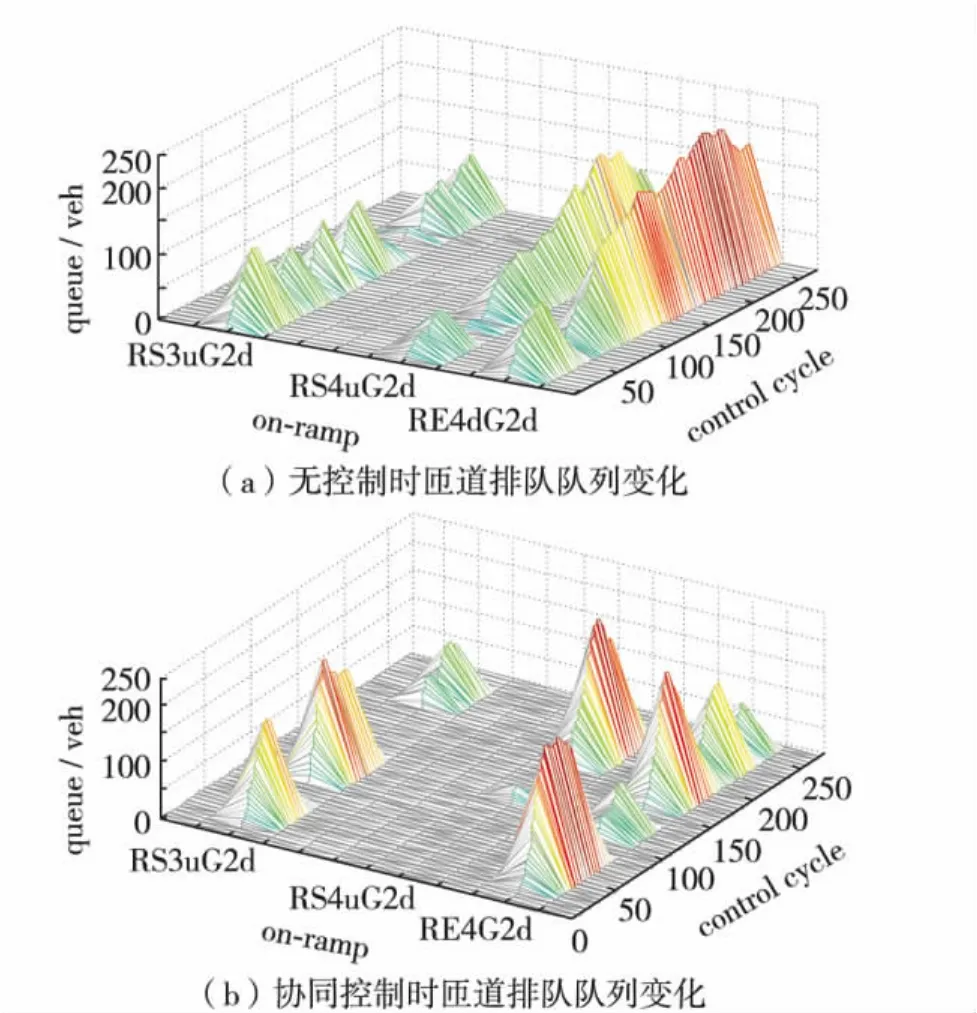
图4 主线关联多匝道排队长度对比 (40 s)Fig.4 Ramp queue profile comparison(40 s)

对比图2和图4，控制周期优化后，无控制和协同控制下相应排队长度对比、总长度值域、排队持续时间和规模均有明显降低.

以40 s为控制周期，各入口匝道在两种控制状态下的bi(k)值见图5.由图5可见，40 s控制时bi(k)绝对值减小并出现震荡变化，明显抑制了2 min周期控制时bi(k)值近于单调地递增或长时间保持一个较高数值的情况.

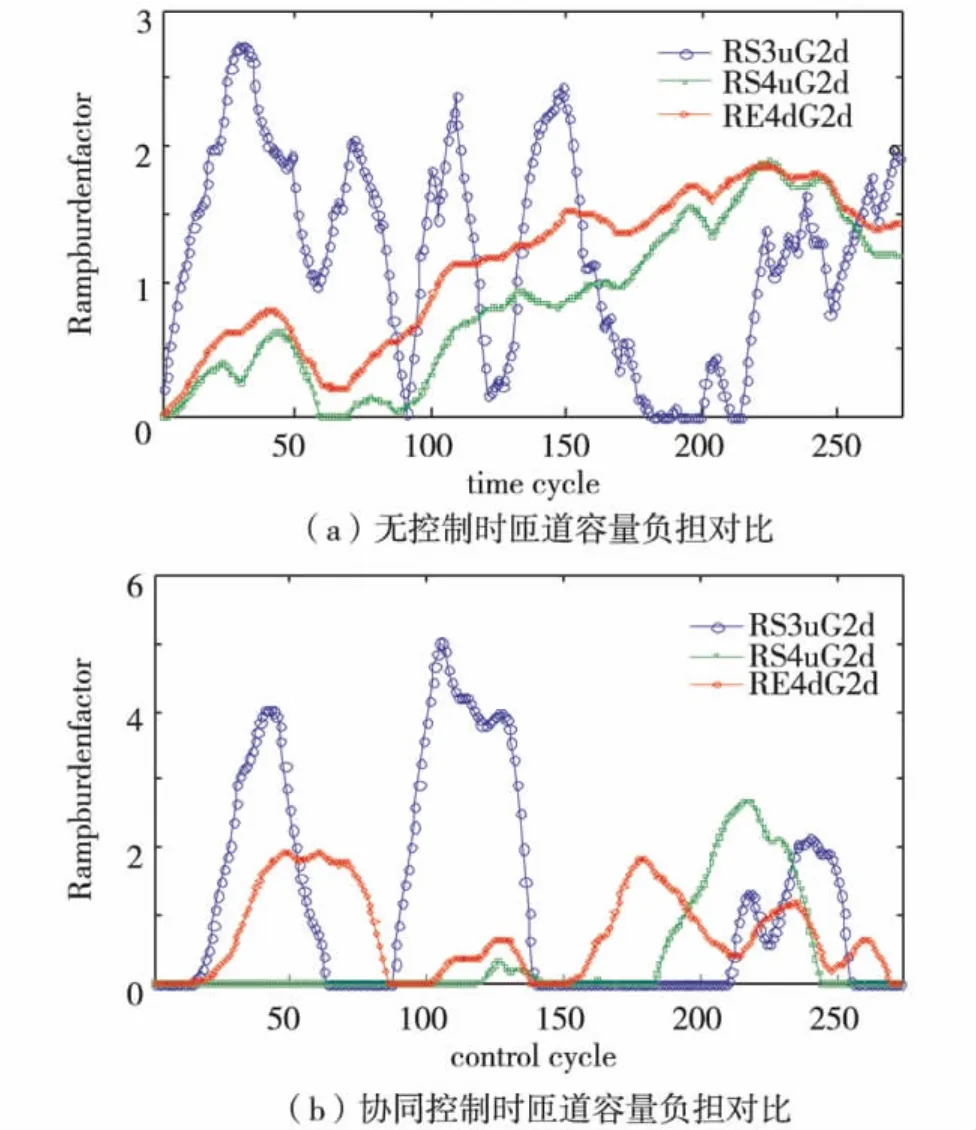
图5 主线关联多匝道容量负担比 (40 s)Fig.5 Ramp queue and capacity comparison profile(40 s)

3.3 平均冗余等待周期数对比

为表征特定周期内所有车辆经历的平均等待周期数，以Tw为基础，设计Nw=Tt/Ts，称冗余等待周期数.以1～3分别表示2 min和40 s为周期控制时的0～30、31～60和61～90个周期，以及0～90、91～180和181～270个周期，Nw-N和Nw-C分别表示无控制和协同控制时的Nw，结果如表1.以2 min周期控制时，在降低Nw方面效果较无控制略差.以40 s周期控制时，Nw前后值域虽无明显变化，但在多个时段内均明显降低，控制效果比无控制时要好.

改进后，控制具有明显的小步幅、高频率及单次汇入量少的特点，有效减少了排队积累，多匝道协同控制优势得到较充分发挥，主线“机动容量”得到有效分配和利用，控制效果有明显改进.

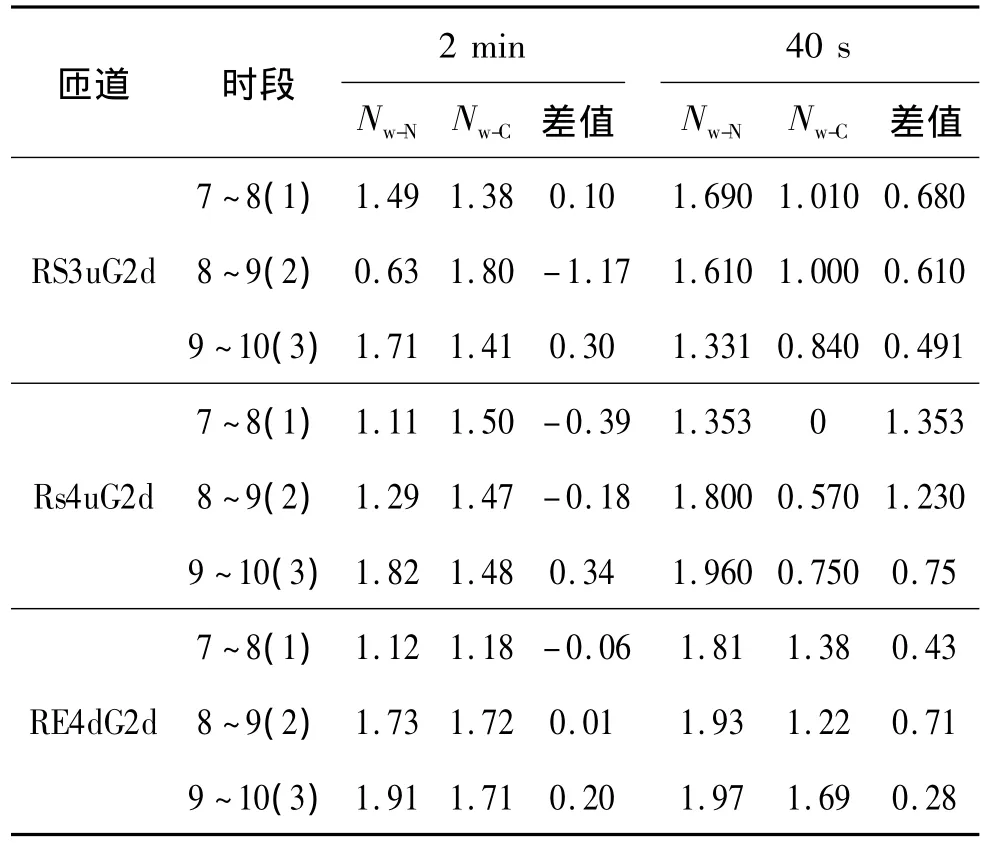
表1 平均冗余等待周期数Table 1 Average redundancy waiting cycle amount

结 语

多匝道协同控制旨在充分疏导通行能力，合理分配路权.采用本文设计的系统控制方法，可以有效提高机动容量的利用效率，挖掘通行潜能，明显均衡各方向的交通等待成本.

/References:

［1］ Levinson D，Zhang L.Ramp meters on trial:evidence from the Twin Cities metering holiday［J］.Transportation Research Part A，2006，40:810-828.

［2］ Zhang L，Levinson D.Ramp metering and freeway bottleneck capacity［J］.Transportation Research Part A，2010，44:218-235.

［3］ Spiliopoulou A D，Papamichail I，Papageorgiou M.Toll plaza merging traffic control for throughput maximizetion［J］.Journal of Transportation Engineering，2010，136(1):67-76.

［4］ Papamichail I，Kotsialos A，Margonis I，et al.Coordinated ramp metering for freeway networks-A model predictive hierarchical control approach［J］.Transportation Research Part C，2010，18:311-331.

［5］ Kotsialos A，Papageorgiou M，Mangeas M，et al.Coordinated and integrated control of motorway networks via nonlinear optimal control［J］.Transportation Research Part C，2002，10:65-84.

［6］ Wu X K，Michalopoulos P，Liu H X.Stochasticity of freeway operational capacity and chance constrained ramp metering［J］.Transportation Research Part C，2010，18:741-756.

［7］ Yousifa S，Al-Obaedi J.Modeling factors influencing the capacity of motorway merge actions controlled by ramp metering ［J］.Procedia Social and Behavioral Sciences，2011，16:172-183.

［8］ Meng Q，Khoo H L.A Pareto-optimization approach for a fair ramp metering［J］.Transportation Research Part C，2010，18:489-506.

［9］ Carlson R C，Papamichail I，Papageorgiou M.Optimal mainstream traffic flow control of large scale motorway networks［J］.Transportation Research Part C，2010，18:193-212.

［10］ Carlson R C，Papamichail I，Papageorgiou M.Optimal motorway traffic flow control involving variable speed limits and ramp metering ［J］.Transportation Science，2010，44(2):238-253.

［11］ Shen W，Zhang H M.Pareto-improving ramp metering strategies for reducing congestion in the morning commute［J］.Transportation Research Part A，2010，44:676-696.

［12］ Jacobson L，Stribiak J，Nelson L.Ramp management and control handbook［R］.Office of Transportation Management Federal Highway Administration，FHWA-HOP-06-001，2006，5-11-5-13，5-28.

［13］ LI Jian，JIA Yuan-hua，CHEN Feng.Local ramp control for urban expressway and related periphery freeway ［J］.Journal of Shenzhen University Science and Engineering，2011，28(3):466-470.(in Chinese)李 健，贾元华，陈 峰.高速公路转向快速路的匝道控制 ［J］.深圳大学学报理工版，2011，28(3):466-470.

［14］ Kotsialos A，Papageorgiou M.Efficiency and equity properties of freeway network-wide ramp metering with AMOC［J］.Transportation Research Part C，2004，12:401-420.

［15］ ZHUANG Yan，LU Shen.A study of the speed flow density relationships on urban roads［J］.Journal of Shenzhen University Science and Engineering，2005，22(4):373-376.(in Chinese)庄 焰，吕 慎.城市道路交通流三参数关系研究［J］.深圳大学学报理工版，2005，22(4):373-376.