基于原模图扩展的QC-LDPC构造方法

龚险峰 陶孝锋 邱乐德

（中国空间技术研究院西安分院，西安710000）（中国空间技术研究院，北京100094）

1 引言

在多数情况下，卫星通信都属于功率受限的通信系统，因而信道编码技术在卫星通信中占有举足轻重的地位。低密度奇偶校验码（LDPC）和Turbo码一样具有逼近Shannon门限的纠错性能，但与Turbo码相比还有一些优势，比如：可以高度并行处理、更低的误码平层等。因此，LDPC引起了广泛的关注，成为继Turbo码后信道编码界的又一研究热点。

校验矩阵从根本上决定了LDPC的纠错性能。国内外学者提出多种校验矩阵构造方法，其中基于原模图的构造方法具有许多优点。由同一原模图扩展构造的任意长度的LDPC都具有类似的结构，其性能上限取决于原模图，可以通过密度演进算法或外部信息转移图分析计算门限值。对于原模图设计，文献[1]提出用模拟退火法优化原模图，文献[2]构造了大量性能逼近Shannon限的原模图。但是，一个好的原模图并非意味着所构造出来的LDPC必然具有优异的性能。实际上，扩展方法不仅影响码的性能，而且还决定了编译码器的硬件实现复杂度。因此，以降低译码门限和误码平层为目标，本文提出了一种基于原模图扩展构造QC-LDPC的方法。

2 原模图与LDPC

LDPC是由稀疏奇偶校验矩阵定义的一种线性分组码，其校验矩阵可以用图来表示，称为Tanner图，如图1所示。Tanner图是一种双向图，由G＝｛（V，E）｝定义，其中V是节点的集合，（V＝Vb∪Vc），E是节点之间相连的边的集合。对于维数为M×N的校验矩阵，Vb＝（v0，v1，…，vN-1）称为变量节点；Vc＝（c0，c1，…，cM-1）称为校验节点。

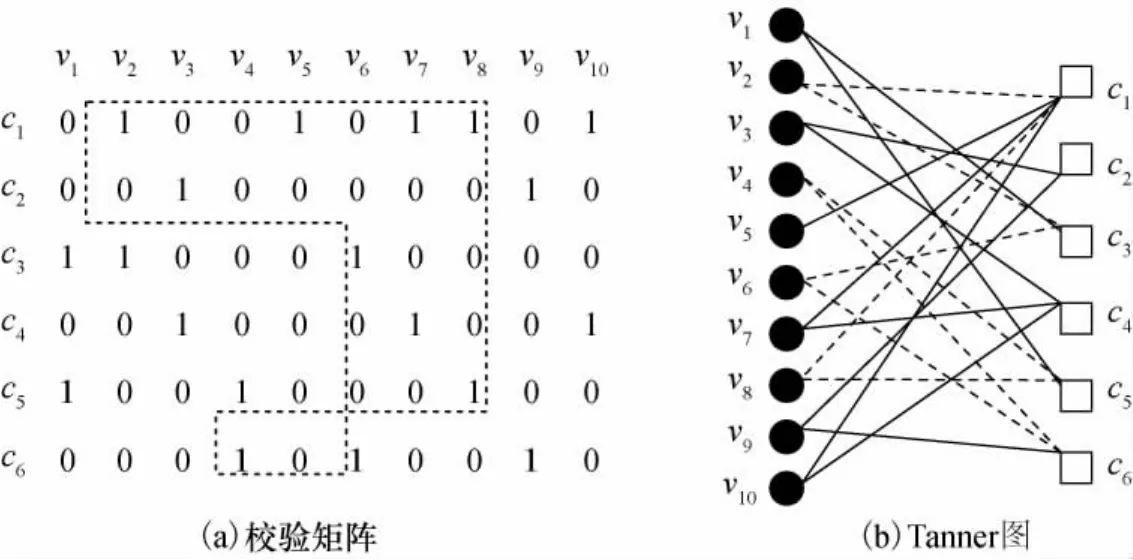
图1 校验矩阵及其对应的Tanner图Fig.1 Parity check matrix and Tanner graph

围长是影响LDPC纠错性能的一个重要参数，虽然构造一个最大可能围长的Tanner图是一个非常难的组合问题，但是构造一个具有相对较大围长且计算复杂度较低的次优算法还是存在的，渐进边增长（PEG）算法是具有此性能的一个常用算法[3]。Tian等人发现，LDPC的误码平台不完全由围长决定，更主要的是和环路的连通度有关，为此提出了近似环路外信息度（ACE）算法[4]。ACE算法和PEG算法相比，稍许损失了编码增益，但降低了误码平层。ACE测度是用来度量环路连通性的参数，一个环的ACE测度定义为

式中k为环路上变量节点的个数；di为变量节点i的度数。

图1显示了一个长度为8的环（v2→c1→v8→c5→v4→c6→v6→c3→v2），其中v2、v4、v6和v8是环上的变量节点，该环路的ACE测度LACE为0。

原模图类似于节点数目较少的Tanner图，但其上允许存在重边。在扩展构造LDPC时，先将原模图复制若干遍，将每个副本称为一个子图，再将处于不同子图中的边进行置换和扰序，使不同子图相互连接起来，所得到的新Tanner图可确定一个LDPC。在原模图的扩展过程中，边置换方式的不同将决定所得新Tanner图中环长及环与周边节点的连通性，从而影响LDPC纠错性能；另一方面，置换方式还将决定所得LDPC是随机的还是结构化的，从而影响编译码器的实现复杂度。

3 原模图扩展算法

对于节点间存在重边的原模图需要进行两步扩展，第一步扩展用于去除节点间的重边，而第二步扩展则是为了使最终的校验矩阵具有准循环结构。为方便叙述，下文中以1／2码率的AR4JA原模图[2]为例进行说明，其结构如图2所示。其中，黑实心圆代表变量节点，带加号的圆代表校验节点，空心圆代表删余的变量节点。该原模图对应的矩阵表达式为

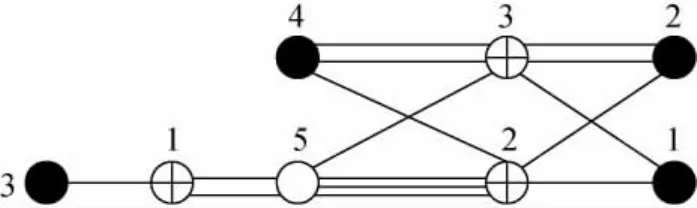
图2 码率1／2AR4JA LDPC原模图Fig.2 Protograph for rate 1／2 AR4JA LDPC

3.1 算法1——原模图的PEG去重边扩展

第一步扩展目的是去除节点间的重边，基本思想是先将原模图扩展L（L大于等于最大重边数）倍，然后进行边置换操作。为了继承原模图的性能特性，边置换只能发生在同一节点扩展出来的L个节点（变量节点或者校验节点）之间。由于L不小于原模图中的最大重边数，只要置换得当就能保证扩展出来的的Tanner图中不再存在重边。在扩展过程中采用PEG算法，使局部围长最大化。但是，与原PEG算法不同的是，扩展过程中要受到上述约束条件的制约。

假设基矩阵的行数和列数分别为M和N，Hs1为第一步扩展后的矩阵。原模图的第一步扩展算法描述如下：

初始化：基矩阵行号i＝0；基矩阵列号j＝1；扩展倍数计数s＝1；Hs1＝0；对矩阵Hs1的变量节点和校验节点进行编号 （分别为1～LN和1～LM）。

1）如果i＝M且s≠L，则i＝1、s＝s＋1，跳到第2）步；如果i＝M且s＝L，则i＝1、j＝j＋1、s＝1，跳到第2）步；如果i≠M，则i＝i＋1，跳到第2）步；如果i＝M、j＝N且s＝L，跳到第6）步。

2）令e＝Hbase（i，j），如果e≠0，则执行第3）步；否则，跳到第1）步。

3）从矩阵Hs1编号为（i-1）L＋1～iL的校验节点中，选择一个行重最小的与变量节点（j-1）L＋s相连。执行第4）步。

4）e＝e-1。如果e＞0，则执行第5）步；否则，跳到第1）步。

5）对矩阵Hs1对应的Tanner图从变量节点（j-1）L＋s进行分层展开[3]，直到展开图中校验节点停止增长或者展开图中已经包含校验节点（i-1）L＋1～iL，展开终止。如果展开终止时，展开图中包含了编号（i-1）L＋1～iL的全部校验节点，则从其中选择一个最后新加入到展开图且行重最小的节点与变量节点（j-1）L＋s相连；否则，从编号为（i-1）L＋1～iL且没有加入展开图的校验节点中，选择一个行重最小的与变量节点（j-1）L＋s相连。跳到第4）步。

6）输出矩阵Hs1，程序终止。

尽管在第一步扩展中采用了PEG算法，但由于扩展倍数较小，矩阵Hs1对应Tanner图中仍然存在大量的小环，且扩展出来的矩阵是非结构化的。

3.2 算法2——基于环检测和ACE测度的准循环扩展

为了得到准循环结构的LDPC，需要对Hs1进行第二步扩展。本算法用维数为V×V（V取决于码长和第一步扩展倍数L）的零矩阵、置换矩阵（单位矩阵及其移位矩阵）分别替换矩阵Hs1中的元素0和1。在扩展过程中，采用PEG算法思想，使局部围长最大化。只要置换矩阵的偏移量取值得当，就能消除原矩阵Hs1中的短环。举例：假设对矩阵Hs1进行倍数为3的准循环扩展，对于Hs1对应Tanner图中的一个长度为4的短环，根据置换矩阵偏移量取值的不同，扩展过程中可能存在多种替换方式，图3为其中两种可能情况。在图3（a）中，替换矩阵Hs1中4个元素1的置换矩阵偏移量分别为0-1-2-1，扩展后的矩阵中依然存在长度为4的短环；在图3（b）中，置换矩阵偏移量分别为0-1-1-1，扩展后得到1个长度为12的环路。文献[5]中给出了一般结论：

定理 假设矩阵Hs1对应Tanner图中存在长度为k的一条封闭路径：（m1，n1）→（m2，n1）→（m2，n2）→ … → （mk，nk）→ （m1，nk），其中1≤i≤k，（mi，ni）为Hs1中的某个非零元素。经准循环扩展后，路径上非零元素对应置换矩阵的偏移量依次为s1→s2→…→sk-1→sk。如果满足条件

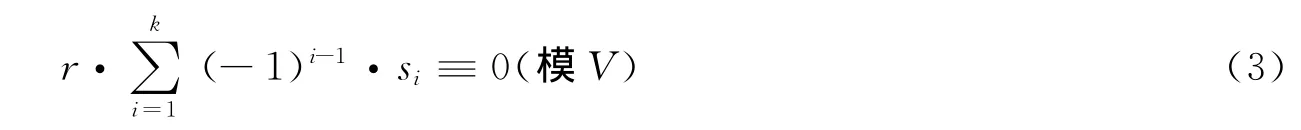
式中r是满足上述条件的最小正整数，则扩展后的准循环矩阵中必存在长度为rk的环。

图3 不同置换矩阵扩展出来的校验矩阵Fig.3 Parity-check matrices based on different permutation matrices

对于给定的扩展因子V，要确定矩阵Hs1中非零元素对应置换矩阵的偏移量使QC-LDPC围长最大化是非常困难的。这里仍然采用PEG算法思想，逐个搜索每个置换矩阵的局部最优偏移量，同时对环路计算ACE测度，从环长和环的连通性两方面对环路进行约束。由于大环对码性能影响较小，为了降低搜索算法的时间复杂度，可以预设一个最大搜索路径长度Kmax，当路径长度超过该值后便停止继续搜索；用Hs2记录第二步扩展后的矩阵，其各元素初始值预置为-1；用矩阵Hs＿temp记录矩阵Hs1中已经完成准循环扩展的部分，其各元素初始值预设为0。第二步扩展算法描述如下：

初始化 行号i＝1，列号j＝1；定义数组A和Β分别记录不同偏移量下的最小环长和最小环路ACE测度。

1）逐列从上到下搜索矩阵Hs1，同时行号i（1≤i≤ML）、列号j（1≤j≤NL）也相应地变化。如果已经搜索完毕，则跳到第5）步；否则，执行第2）步。

2）若i＝1或j＝1，则Hs2（i，j）＝δ、Hs＿temp（i，j）＝Hs1（i，j），其中δ为 [0，V-1]范围内取值的随机整数（δ也可以取一个固定的值），然后跳到第1）步；否则，令Hs＿temp（i，j）＝Hs1（i，j）、v＝0、A[v]＝∞、B[v]＝∞，然后执行第3）步。

3）令Hs2（i，j）＝v。在矩阵Hs＿temp对应的Tanner图上，搜索从校验节点i、变量节点j往下延伸的所有路径，用变量k记录每条路径的长度（对于每条路径，当k＞Kmax或者路径无法继续延伸后停止）。如果没有止于校验节点i的封闭路径，直接跳到第4）步；否则，对于每条止于校验节点i的封闭路径，按照公式（3）计算准循环扩展后的环路长度p并按照公式（1）计算其ACE测度值q。如果p＜A[v]，令A[v]＝p；如果q＜B[v]，令B[v]＝q。搜索完成后，执行第4）步。

4）如果v＜V-1，则令v＝v＋1，跳到第3）步；否则，对数组A进行排序，得到A中最大值对应的序号t（若A中存在多个相同的最大值，则比较对应数组Β中的元素，选择数值大的元素对应的序号），令Hs2（i，j）＝t，跳到第1）步。

5）输出矩阵Hs2。

对于不存在重边的原模图，不需要进行第一步扩展，直接对原模图进行第二步扩展便能得到QC-LDPC。对于矩阵Hs2中的任意元素，若Hs2（i，j）＝-1，则用V×V的零矩阵替代；否则，用偏移量为Hs2（i，j）、维数为V×V的置换矩阵替代，由此得到QC-LDPC校验矩阵。

4 性能仿真

利用上述算法，基于AR4JA原模图构造了两个QC-LDPC，码率都为0.5，码长分别为2 048和8 192。为了降低搜索算法的时间复杂度，最大搜索路径长度设置为16。仿真条件：加性高斯白噪声信道（AWGN）和乘译码算法（SPA），最大迭代次数为200。在CCSDS 131.1-O-2深空通信标准中，采用的便是AR4JA原模图扩展构造的QC-LDPC，具有优异的性能[6]。图4中给出了性能仿真曲线，可以看出误码率为10-6时，两个码的译码门限分别为1.3dB和1.9dB，与CCSDS 131.1-O-2标准上的相同码率、码长的码性能基本一致（标准上对应码性能分别为1.2dB和1.9dB）。

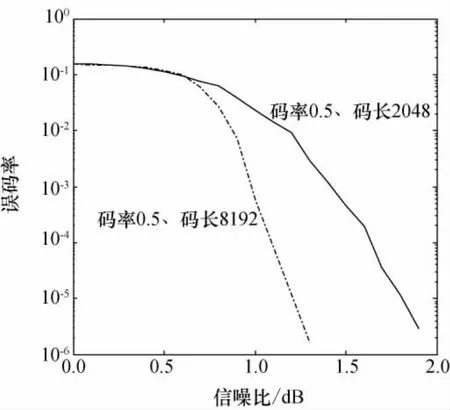
图4 误码性能仿真Fig.4 BER versus SNR simulation results

5 结束语

经过参数优化得到的原模图，为构造性能优异的LDPC创造了前提条件，但其最终性能仍然受制于扩展算法。本文提出了一种基于原模图扩展构造QC-LDPC的方法，在扩展过程中，以环长和环路ACE测度最大化为目标，通过搜索算法规避连通性差的短环。由于参数优化是依次进行的，所述算法在环长和ACE测度方面不是全局最优的，但具有局部最优性。仿真结果表明，采用该方法构造的LDPC，在译码门限和错误平层两方面都具有良好的表现，证明了所述算法的有效性。同时，所构造的LDPC具有准循环结构，适于工程实现。但是，在准循环扩展过程中，参数优化次序对码性能的影响，仍然是一个需要进一步研究的问题。

[1]THORPE JEREMY.Analysis and design of protograph based LDPC codes and ensembles [D].Pasadena：California Institute of Technology，2005.

[2]DARIUSH DIVSALAR，SAMUEL DOLINAR，CHRISTOPHER R JONES，et al.Capacity-approaching protograph codes[J].IEEE Journal on Selected Aeras in Communications，2009，27 （6）：876-888.

[3]HU XIAOYU，ELEFTHERIOU EVANGELOS，DIETER MICHAEL ARNOLD.Progressive edge-growth tanner graphs[C].IEEE GlobeCom，2001，2：995-1001.

[4]TIAN TAO，JONES R CHRISTOPHER，VILLASENOR D JOHN，et al.Selective avoidance of cycles in irregular LDPC code construction [J].IEEE Transactions on Communications，2004，52（8）：1242-1247.

[5]SEHO MYUNG，KYEONGCHEOL YANG，JAEVOEL KIM.Quasi-cyclic LDPC codes for fast encoding [J].IEEE Transactions on Information Theory，2005，51（8）：1788-1793.

[6]THE CONSULTATIVE COMMITTEE FOR SPACE DATA SYSTEMS.Low density parity check codes for use in near-earth and deep space applications [S].CCSDS 131.1-O-2，Orange Book，Issue 2，Washington，DC，2007.