基于离散粒子群算法的多飞行器在轨服务任务分配

张琪新 孙富春 许斌 刘华平

（1海军航空工程学院，烟台264001）

（2清华大学，北京100084） （3智能技术与系统国家重点实验室，北京100084）

1 引言

飞行器在轨服务（On-orbit Service，OOS）是指在空间通过人、机器人或两者协同完成涉及延长各种飞行器寿命、提升执行任务能力的一类空间操作[1-2]。

目前，国内外对在轨服务任务分配已开展了相关的研究，但针对服务飞行器的协同任务分配研究较少。文献[3]对圆轨道上一颗服务飞行器执行多项任务的在轨服务规划问题进行了研究，但没有考虑服务飞行器的服务时间；文献[4]对同步轨道上一颗服务飞行器执行多项任务的最优服务策略进行了研究，但不能够解决协同多个服务飞行器之间的问题；文献[5]建立了双冲量远程交会的能量时间模型，但仅考虑飞行器能量消耗和时间两项因素，讨论也仅限于单个飞行器；文献[6]采用整数规划方法通过设计决策变量和形式化各种约束，较好地解决了任务指派问题，但是并没有综合考虑飞行器在整个服务过程中自身的损耗；文献[7]以对目标的毁伤最大和自身消耗最小为任务分配的目标函数，但没有考虑执行任务的消耗时间这一重要因素，而完成任务的时间是反映效能的关键指标之一。文献[8]针对分布式协同控制，采用基于投标、竞标等市场机制的合同网方法，协调多个飞行器间的任务，具有通信量少、鲁棒性能好等优点，但各飞行器对自身收益和代价的评价局限于任务的平衡，没有考虑到自身指标。使用线性规划、动态网络流等方法对多任务分配问题进行建模[9-11]，虽然这些模型简单、易于实现，但目标函数过于简单，不能完全描述关键指标。服务飞行器协同任务分配中，各飞行器的控制必须相互协调，采用基于动力学方法建立双脉冲优化制导模型，综合考虑飞行器消耗、提供服务所获收益最大、轨道转移所需能量以及消耗时间关键指标，协同多飞行器进行任务分配。

本文针对在轨服务飞行器任务分配问题的特点，设计了新的离散粒子群位置与速度更新公式，提出了一种新的在多约束条件下，基于离散粒子群算法的多服务飞行器目标分配方法。

2 任务分配模型

2.1 任务场景

空间在轨服务飞行器得到指令后，需要从准备轨道转移至靠近目标卫星的服务轨道。其中，服务飞行器是主动的，而需要服务的目标飞行器是被动的，轨道转移过程可用图1简单描述。服务飞行器运行在低轨道上，在综合考虑自身性能和周围环境等约束条件下，根据任务分配的结果合理地实施Lambert双脉冲轨道转移至目标卫星的高轨道上，在交会初始时刻施加第一次脉冲，在靠近目标卫星施加第二次脉冲，单圈Lambert变轨示意图见图2。在整个在轨服务任务过程中，服务飞行器始终保持在目标卫星的轨道上。

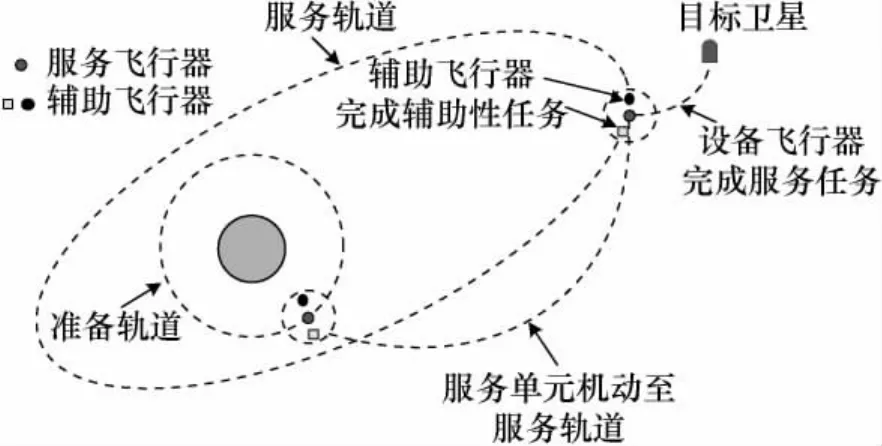
图1 空间在轨服务示意Fig.1 Space on-orbit servicing

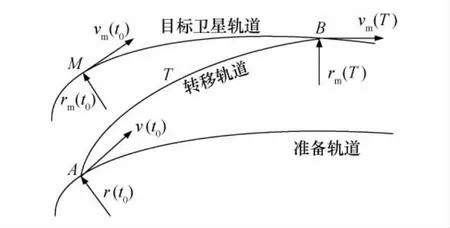
图2 单圈Lambert变轨示意Fig.2 Lap Lambert maneuver

2.2 数学模型

（1）决策变量

设有U颗在轨部署的服务飞行器，在某刻有T颗具有不同任务优先级的目标飞行器等待服务，根据该规划问题的特点，决策变量可以定义为

式中u＝1，2，…，U；t＝1，2，…，T。

服务飞行器目标分配是以整个编队的整体收益最优作为目标的，而目标飞行器价值、服务飞行器消耗以及能量时间消耗是评价效能主要指标[12-13]。

（2）飞行器消耗最小指标

执行任务往往在规定的时间内，选择最容易服务的飞行器，设计相应的轨道，从而达到降低飞行器损耗的目的。设aut为服务飞行器对目标飞行器服务后的消耗，如可能出现的部件失效、软硬件故障以及零部件的磨损。对服务飞行器进行任务分配，使得所有服务飞行器消耗之和最小，即

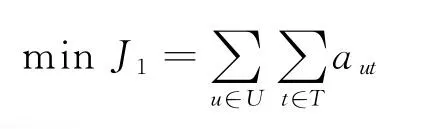
（3）目标飞行器价值收益最大指标

目标价值收益最大指标通过对服务飞行器执行任务时所获取目标价值的评估，来引导目标分配的优化和决策向着服务效能最大化的方向进行。该指标使服务飞行器趋向于服务最优价值的目标。综合考虑目标价值V、确认概率Pc、剩余服务能力1-aut，则服务飞行器U服务目标飞行器T时，收益为Vut＝V·Pc·（1-aut）。其中，Pc表示服务飞行器准确到达任务区域、发现目标并且正确识别出目标的概率，为每个服务飞行器分配任务，使得总的收益最大，即

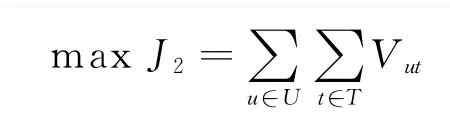
（4）能量时间最优模型

在得到既定任务后需要对在轨服务飞行器进行轨道机动，自主、快速、精确和大范围轨道机动技术为各种应用提供了可靠的保证。远程导引变轨在整个任务分配活动中起着非常重要的作用，合理的导引变轨还能够节省能量以及所需时间。同时考虑燃料消耗和转移时间，建立性能指标，使得能量时间消耗最小，即

式中 Δv1为交会初始时刻所需的速度增量；Δv2为交会末时刻所需的速度增量；t为交会变轨所要求的时间；0≤k≤1为比例系数。根据交会变轨时间t就能求出Lambert双脉冲变轨所需的能量消耗，寻找最佳交会时间，使得变轨能量消耗也最小。

（5）约束条件

服务飞行器任务分配应满足以下约束条件：

2）对于每个目标，无论采取什么方式的服务，对目标价值收益不大于该目标的自身价值：

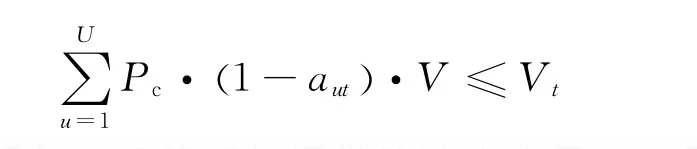
3）Δv1＋Δv2≤Δv，Δv表示服务飞行器所能提供的速度增量，即服务飞行器执行任务需要的速度增量必须小于其所能提供的速度增量。

综上所述，服务飞行器任务分配的性能指标函数可以表示为

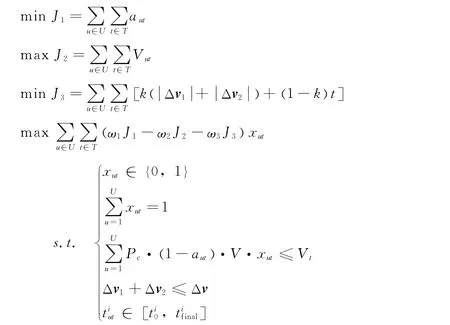
式中ω1、ω2、ω3为权系数，反映了每个子目标的重要程度。

任务分配问题的特点是随着问题规模的增大，决策变量的个数和决策向量的维数将大为增加，难点是怎样在满足各种约束条件的基础上，综合考虑各项指标组成的目标最优值，若仍用传统的最优算法求解这个组合优化问题时，计算量将非常大，从而导致求解困难，甚至无法求解。针对这一情况以及服务飞行器协同目标分配问题特点，设计了一种新的离散粒子群目标分配算法。

3 离散粒子群算法

粒子群优化算法（Particle Swarm Optimization，PSO）是Kennedy和Eberhart于1995年提出的，有着个体数目少、计算简单、鲁棒性好等优点。PSO算法中，每个粒子就是一个备选解，多个粒子共存、合作寻优。每个粒子根据自身和粒子群的经验，在问题空间中向更好的位置 “飞行”，搜索最优解。粒子本身找到的最优解称为个体最优值pbest，就是每个粒子在飞行过程所经历过的最优位置。整个群体目前找到的最优解称为全局最优值gbest，就是整个群体所经历过的最优位置[14-16]。由于标准的粒子群算法具有连续本质，不太适宜于求解离散问题。为了将其用于服务飞行器协同目标分配问题的求解，根据该问题的特点，在分析多约束基础上，设计了自然数编码的离散粒子群算法，建立了粒子与实际问题的对应关系，并且对标准粒子群算法作了相应的改进[17]。

3.1 离散粒子群编码方式

服务飞行器协同目标分配的决策关键在于确定任务目标由哪个飞行器来执行。因此，这里采用自然数编码方式来表达，每个粒子长度等于目标总数，粒子由按目标编号顺序排列的服务飞行器分配编号组成，表示一种可能的分配方案。例如，目标飞行器数目n取3，目标数目m取4，如图3所示，表示第2个服务飞行器服务第1个目标，第3

个服务飞行器服务第2个目标，第1个服务飞行器同时对第3个目标和第4个目标进行服务。保证约束条件中对每一个目标必须分配一个服务飞行器的限制，单位粒子取值范围为[1，n]。

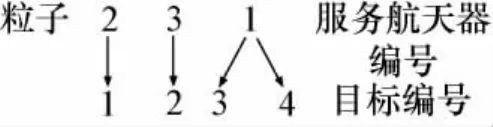
图3 粒子编码Fig.3 Particle code

3.2 离散粒子群算法的位置和速度更新公式

粒子的新位置是粒子的速度、个体极值和全局极值相互作用的结果。根据服务飞行器协同目标分配问题的实际特点，对粒子群算法的位置和速度更新公式进行重新定义，即

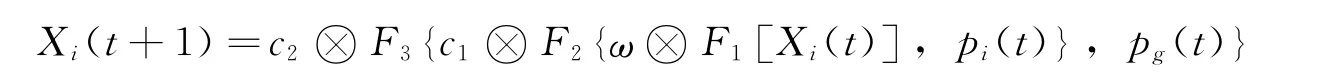
式中Xi＝（xi1，xi2，…，xim）为粒子i在迭代中的位置；pi＝（pi1，pi2，…，pim）为粒子i的个体极值；pg＝（pg1，pg2，…，pgm）为全局极值；ω为惯性权重；c1是认知系数，调节向pi的飞行步长；c2是社会系数，调节向pg的飞行步长。F1[Xi（t）]是关于粒子Xi（t）的函数，其作用是考虑粒子本 身 速 度 对 其 位 置 变 化 的 影 响；F2[Xi（t），pi（t）]为Xi（t） 对pi（t） 的 学 习 操 作；F3[Xi（t），pg（t）]为Xi（t）对pg（t）的学习操作。位置更新公式由三部分构成，设Ψi为临时变量：

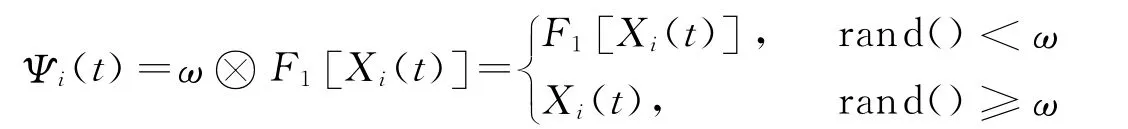
这是粒子的“惯性”部分，表示粒子对自身飞行速度的思考。其中ω⊗F1[Xi（t）]表示粒子的速度，即为一个概率为ω的目标置换操作，它的实现方法为：由rand（）产生一个区间[0，1]上的随机数r，如果r＜ω，将对粒子进行置换操作Ψi（t）＝F1[Xi（t）]，即产生两个在 [1，m]之间不同的随机数a和b，然后将粒子位置矢量的第a个数值与第b个数值互换，也就是将服务第a个目标的服务飞行器与服务第b个目标的服务飞行器进行互换，如图4所示；如果r≥ω，则Ψi（t）＝Xi（t）。

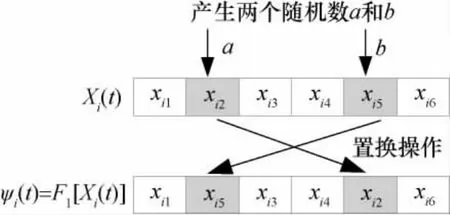
图4 目标置换操作Fig.4 Target replacement

离散粒子群算法的流程图如图5所示。

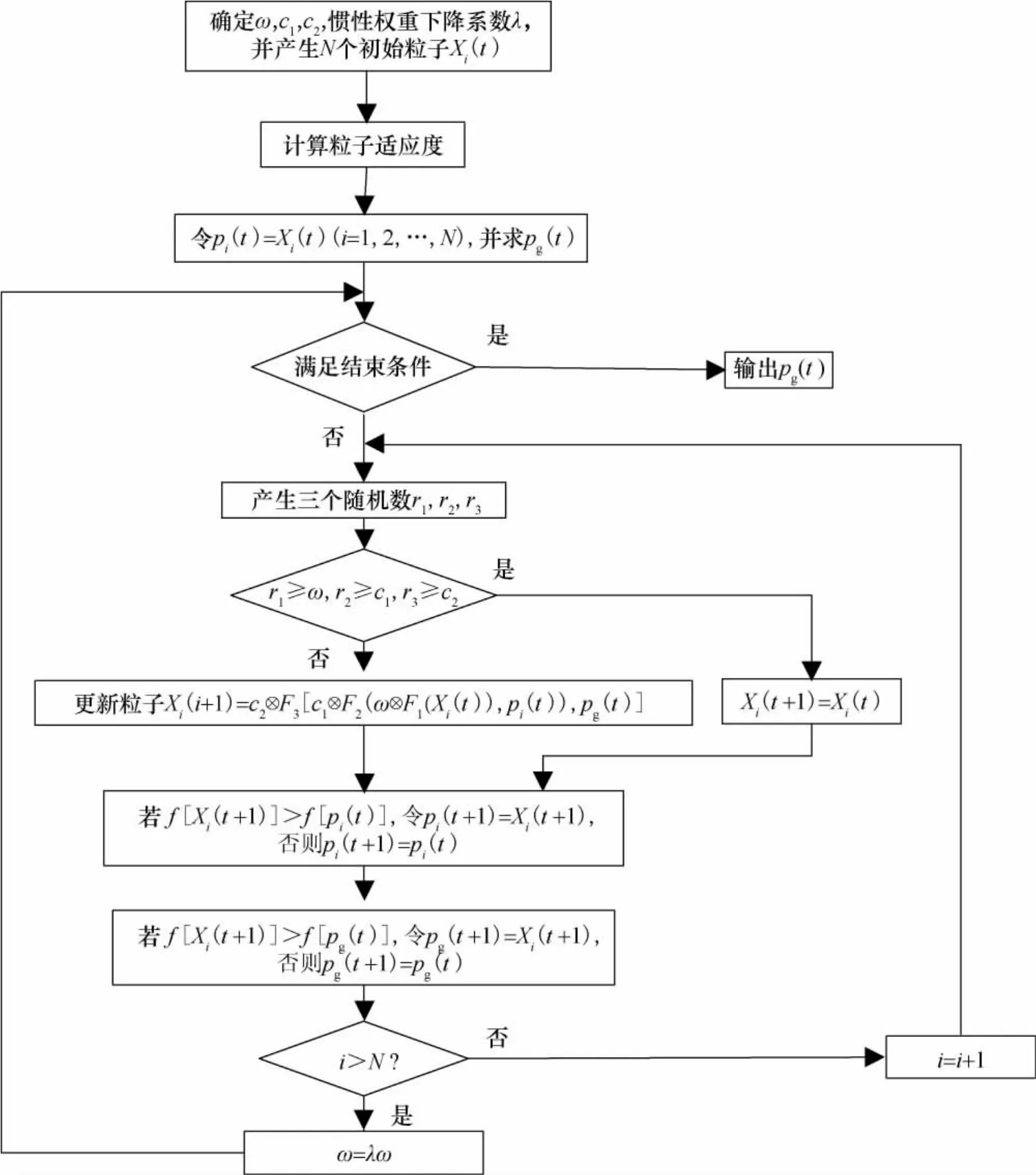
图5 离散粒子群算法流程Fig.5 Flow chart of DPSO

4 仿真试验

假设在同一轨道上部署了5个服务飞行器，它们具有不同的服务和机动能力，但一个飞行器只能对一颗目标飞行器提供在轨服务。现有处于不同轨道上的目标飞行器，要求在规定的交会时间内完成对目标飞行器的在轨服务，使整体效能达到最佳。算例1和算例2的初始轨道要素如表1和表2所示。

两种算例的时间约束为50min，任务要求准时与目标飞行器交会，实施在轨服务。

服务飞行器实施远程轨道机动的交会时间设定在1 000～3 000s之间，通过搜索某一时刻对应速度增量，能够找出最小能量消耗，将其代入任务分配模型中，结合假设求解如下两种算例。

（1）5个服务飞行器对3个目标飞行器服务

假设有5个服务飞行器和3个目标飞行器，pc＝1。为便于与文献[18]中的模型和算法相比较，目标的价值、剩余服务能力都采用文献[18]中的数据，如表3所示（剩余服务能力和目标价值均是根据飞行器轨道参数进行的假设）。

在算例中，分别采用遗传算法和离散粒子群算法对上述问题进行仿真，并将迭代30次后两种算法的最优、平均、最差解进行了对比，得出最终的服务飞行器任务分配的结果如表4所示。通过表4的数据可以知道，在服务飞行器和目标飞行器规模不大的情况下，两种算法得到的最优解和任务分配的结果是一致的，最优方案及对应时间的最小速度增量如表5所示。在小规模的任务分配中，虽也能够得到最优的分配结果，但两种算法的优劣性差别不大。后面大规模任务分配算例中，将会体现出离散粒子群算法的优越性。

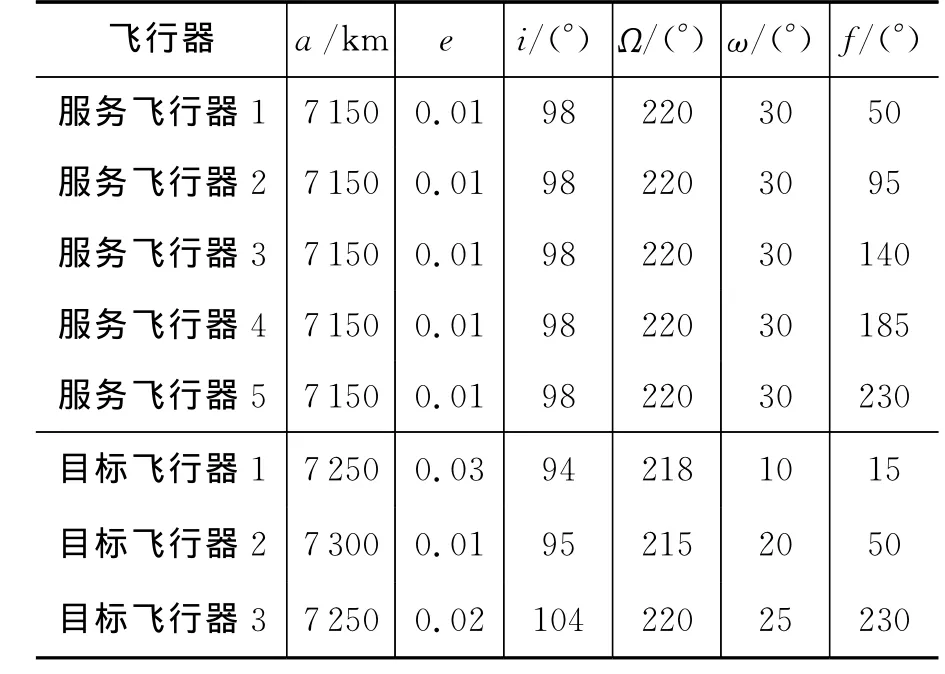
表1 算例1服务飞行器和目标飞行器初始轨道要素Tab.1 Initial orbital elements in example 1

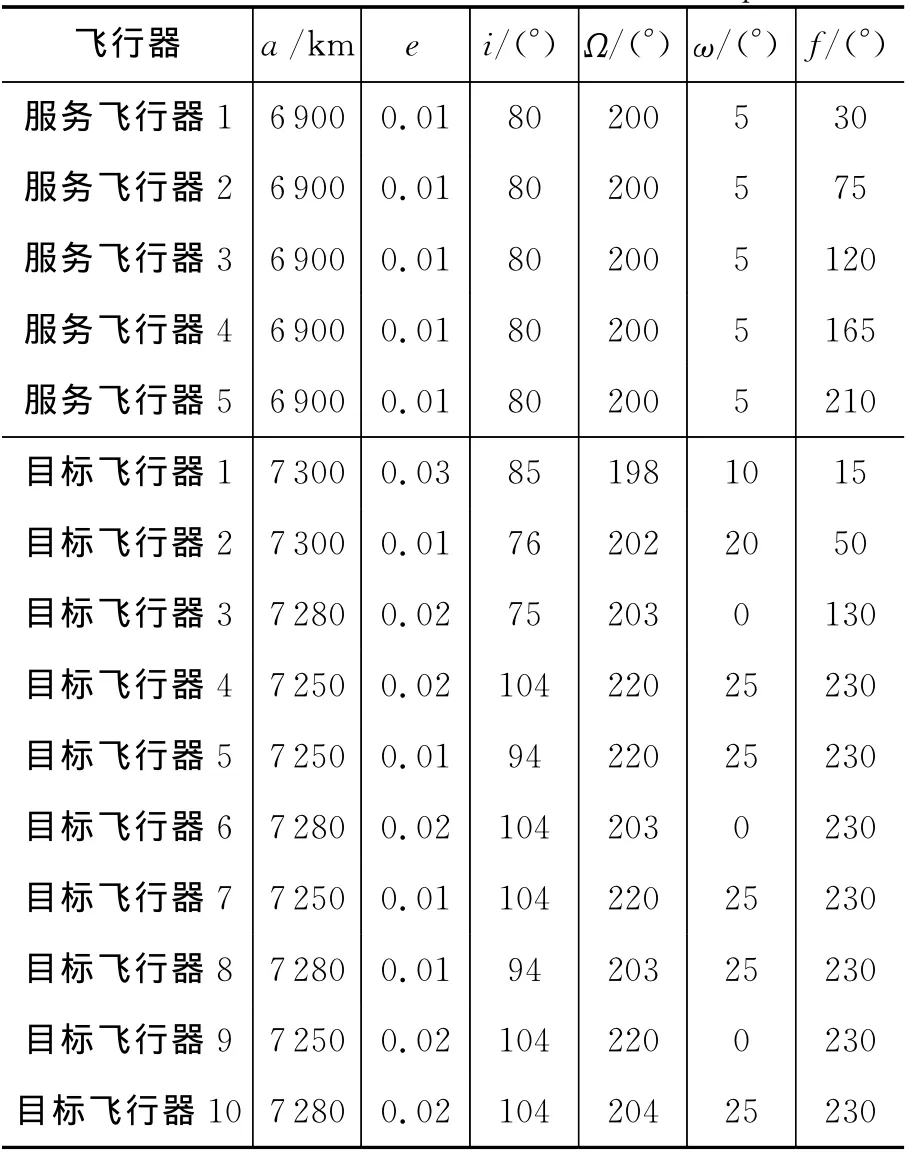
表2 算例2服务飞行器和目标飞行器初始轨道要素Tab.2 Initial orbital elements in example 2

表3 服务器剩余服务能力和目标价值Tab.3 Surplus capacity and target value in spacecrafts

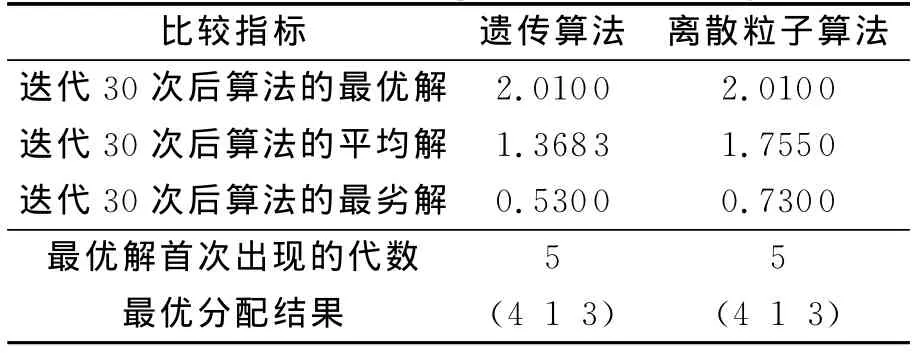
表4 两种算法的性能比较Tab.4 Performance comparison of two algorithms

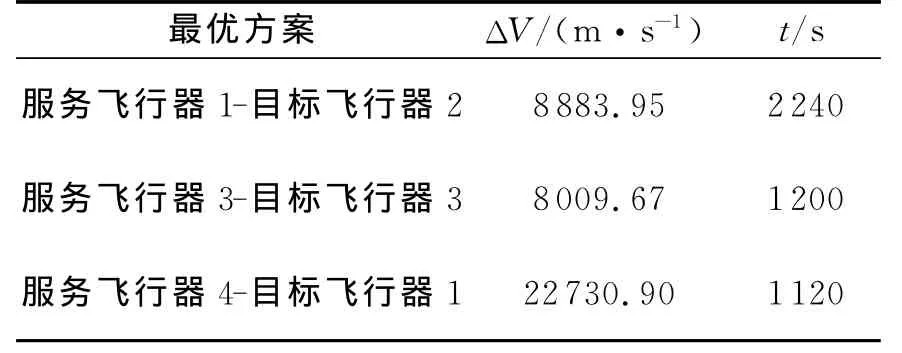
表5 仿真结果Tab.5 The simulation results

（2）5个服务飞行器对10个目标飞行器服务

假设有5个服务飞行器和10个目标卫星，pc＝1。为便于与文献[19]中的模型和算法相比较，目标的价值、剩余服务能力都采用文献[19]中的数据。

在算例中，两种算法在迭代30次过程中的最优、平均、最差解的变化曲线及比较结果如图6～图8和表6所示。大规模的任务分配能够体现出两种算法的差异：从图8中可以看出，离散粒子群算法比遗传算法收敛特性要好，能够比较快速地找到最优解，而且在离散粒子群平均解的变化曲线也可以看出，即使在迭代的后期，也不会出现粒子趋同的现象，说明该算法具有较强的寻优能力。

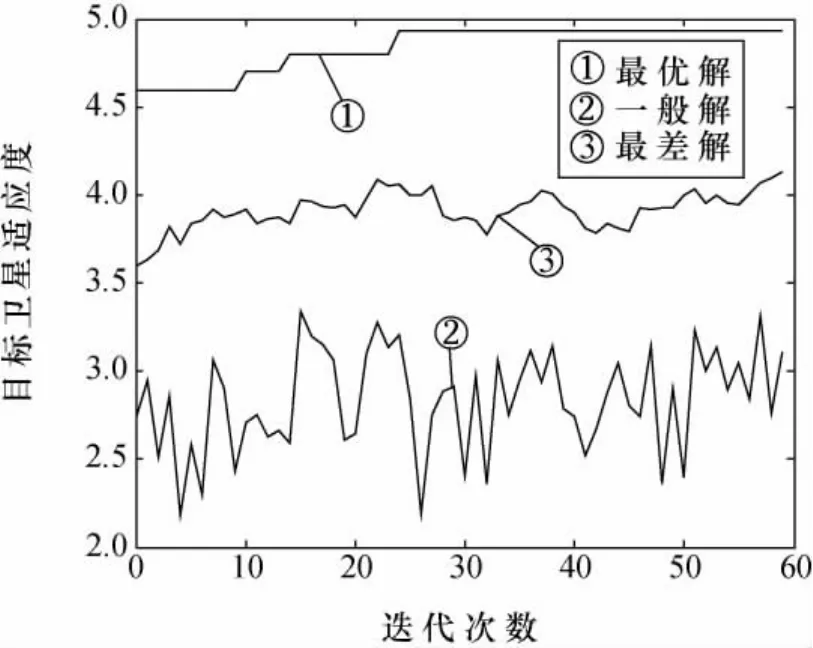
图6 遗传算法收敛曲线Fig.6 GA convergence curve

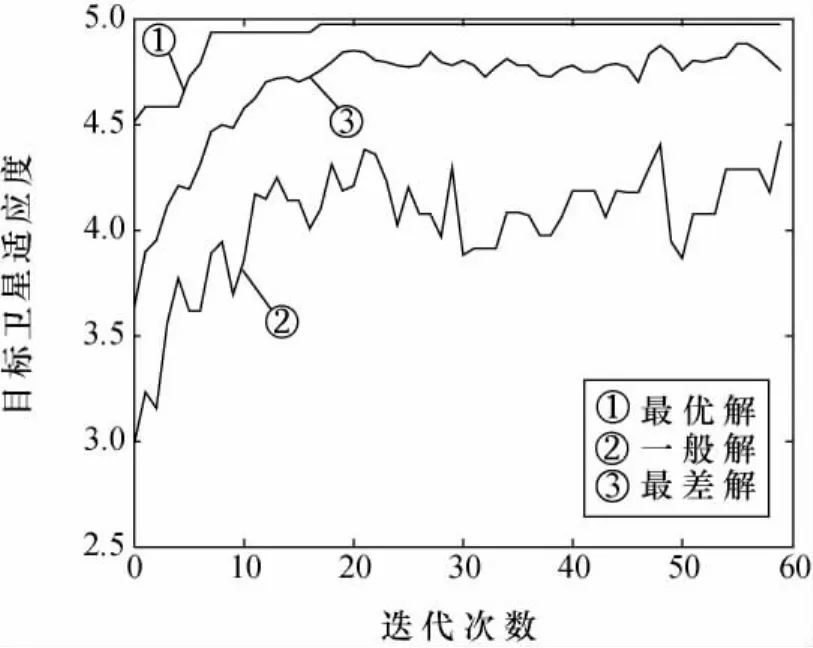
图7 离散粒子群算法收敛曲线Fig.7 DPSO convergence curve

图8 两种算法性能比较Fig.8 Performance comparison of two algorithms

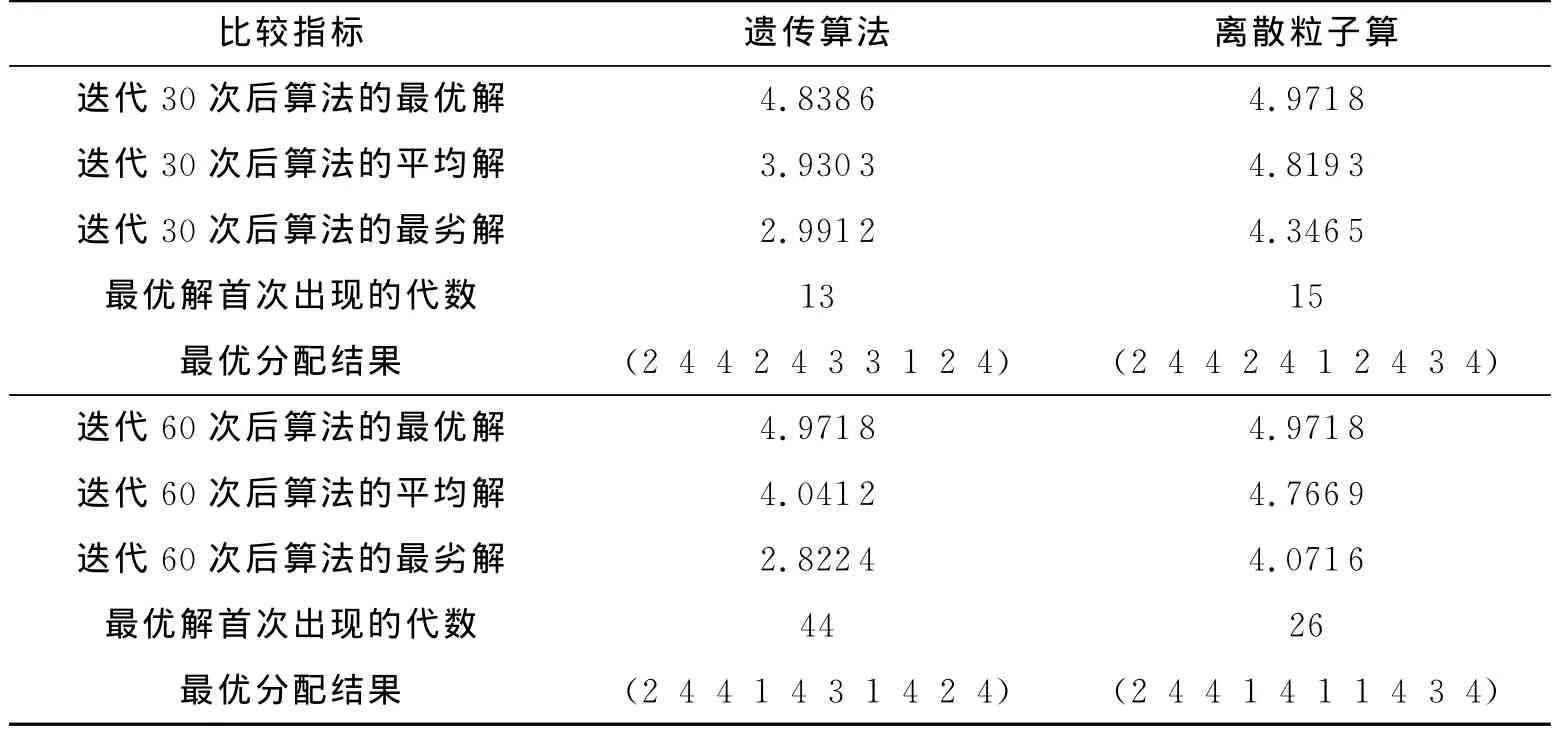
表6 不同迭代次数下两种算法性能比较Tab.6 Performance Comparison of Two Algorithms under different iteration

由计算结果可知，该任务分配方案可使服务飞行器在指定的任务完成时间内，以最大的效益完成服务任务，且满足各项约束条件，保证了轨道机动过程中能量消耗最少，从而较好地解决了在轨服务任务分配问题。

5 结束语

本文根据在轨服务飞行器协同任务分配问题的特点，设计了新的离散粒子群位置与速度更新公式，提出了一种基于离散粒子群算法的多服务飞行器目标分配方法。仿真结果表明，改进的粒子群算法能够快速稳定地找到最优分配方案，有效地解决多约束条件下的服务飞行器任务分配问题。在本文的静态研究基础上可以进一步分析任务状态变化的情况，以及这些变化过程中的不确定性，另外，还可以考虑当服务飞行器所带燃料有限时如何进行任务分配的问题。本文的研究工作为研究动态分配问题提供了较好的基础。

[1]DONALD M WALTZ.On-orbit servicing of space system [M].Krieger Publishing Company，Malabar，Florida，1993.

[2]崔乃刚，王平，郭继峰，等.空间在轨服务技术发展综述 [J].宇航学报，2007，28（4）：33-39.CUI NAIGANG，WANG PING，GUO JIFENG，et al.A review of on-orbit servicing [J].Journal of Astronautics，2007，28（4）：33-39.

[3]SHEN HAIJUN.Optimal scheduling for satellite refuelling in circular orbits [D].Georgia：Georgia Institute of Technology，2003.

[4]CHENG CHEUGCHUUG，SMITHSF.Appling constraint satisfaction techniques to job shop scheduling[R].Pittsburgh：Carnegie Mellon University，1995.

[5]HU LAIHONG，SUN FUCHUN，XU BIN，et al.On-orbit long-range maneuver transfer via EDAs[C].IEEE World Congress on Computational Intelligence，2008：2343-2347.

[6]任仙海，杨乐平，朱彦伟.基于整数规划的在轨服务任务指派问题研究 [J].装备指挥技术学院学报，2008，19（2）：52-56.REN XIANHAI，YANG LEPING，ZHU YANWEI.Research on the on-orbit servicing mission assignment based on integer programming [J].Journal of the Academy of Equipment Command and Technology，2008，19（2）：52-56.

[7]CURZJ B，JR C，CHEN G.Particle swarm optimization for resource allocation in UAV cooperative control[C].AIAA Guidance，Navigation，and Control Conference，Rhode Island，2004：16-19.

[8]LEMAIRE T，ALAMI R，LACROIX S.A distributed tasks allocation scheme in multi-UAV context[C].2004IEEE International Lonference on Robotics and Automation，2004：3622-3627.

[9]SPENCER D B，KIN Y H.Optimal spacecraft rendezvous using genetic algorithm [J].Journal of Spacecraft and Rockets，2002，39（6）：859-865.

[10]NYGARD K E，CHANDLER P R，PACHTER M.Dynamic network optimization models for air vehicle resource allocation[C].American Control Conference，Arlington，VA，2001：1853-1858.

[11]霍霄华，陈岩，朱华勇，等.多UCAV协同控制中的任务分配模型及算法 [J].国防科技大学学报，2006，28（3）：83-88.HUO XIAOHUA，CHEN YAN，ZHU HUAYONG，et al.Study on task allocation model and algorithm for multi-UCAV cooperative control[J].Journal of National University of Defense Technology，2006，28（3）：83-88.

[12]FAN CHUNXIA，WAN YOUHONG.An adaptive simple particle swarm optimization algorithm [C].Control and Decision Conference，2008：3067-3072.

[13]PAN Q K，TASGETIREN M F，LIANG Y C.A discrete particle swarm optimization algorithm for the no-wait flowshop scheduling problem with makespan criterion [C]／／ Proceeding of the Int Workshop，UK Planning and Scheduling Special Interest Group，2005：31-41.

[14]VENTER G.Particle swarm optimization [C].43rd AIAA／ASME／ASCE／AHS／ASC Structures，Structural Dynamics，and Materials Conference，Denver，2002.

[15]BERGH F，ENGELBRECH A P.A cooperative approach to particle swarm optimization[J].IEEE Transactions on Evolutionary Computation，2004，8 （3）：255-239.

[16]JI C L，YUAN P.Particle swarm optimization for mobile Ad Hoc networks clustering [C].Proc.2004 IEEE International Conference on Networking，Sensing＆Control，Taipei，Taiwan，2004（3）：225-239.

[17]叶文，朱爱红，潘长鹏，等.多UCAV协同目标分配算法研究[J].系统工程与电子技术，2010，32（1）：104-108.YE WEN，ZHU AIHONG，PAN CHANGPENG，et al.Cooperation mission assignment algorithm for multi-UCAV[J].Systems Engineering and Electronics.2010，32（1）：104-108.

[18]CURZ J B，JR C，CHEN G.Particle swarm optimization for resource allocation in UAV cooperative control[C].AIAA Guidance，Navigation，and Control Conference and Exhibit，Rhode Island，2004：16-19.

[19]雷英杰，张善文，李续武，等.MATLAB遗传算法工具箱及应用 [M].西安：西安电子科技大学出版社，2005：128-130.