卫星接收系统抗干扰的卷积盲分离算法

温媛媛 陈豪

（中国空间技术研究院西安分院，西安710100）

1 引言

卫星通信受自身特点的限制和环境的影响，不可避免地存在各种干扰，因此具有一定的抗干扰能力是其基本要求。现有的抗干扰方法很多，但它们都有各自的局限性，当卫星通信信号和干扰信号在频域和时域上都混叠在一起时，使用普通的抗干扰方法很难达到抗干扰的目的。可以考虑把盲信号分离技术应用到卫星通信抗干扰中，用盲信号分离方法来分离出通信信号和干扰。

近年，盲分离已成为信号处理领域的一个热点，涌现出了许多盲分离算法[1-3]。盲分离是在源信号和传输信道参数未知的情况下，仅根据源信号的统计特性，从观测信号中分离出源信号的过程[4]，盲分离要求源信号相互之间是统计独立的。由于卫星通信信号和干扰信号来自不同的发射源，它们可以被假设是统计独立的，且它们的传输信道参数也是未知的，具备了盲分离的基本要求，所以可以把盲分离技术应用到卫星接收系统抗干扰中。盲分离所研究的模型主要分为瞬时混叠、卷积混叠及非线性混叠。而在实际的信号环境中，卫星上接收设备所接收到的信号基本上都是源信号与多径传输信道的卷积混叠，也就是说，卫星上接收到的信号是有用通信信号与干扰信号之间卷积混叠而成的信号。

针对这种情况，本文对卷积混叠盲分离算法进行研究，对文献[5]的算法（记作G-JBD）进行改进，提出一种新的联合对角化算法（记作NH-JBD），且把它应用到卫星通信抗干扰中。

2 卫星上接收信号的卷积盲分离模型

考虑一个两输入两输出系统，卷积盲分离模型可表示为

式中X（t）是观测信号，X（t）＝[x1（t），x2（t）]T；H为未知的传递通道矩阵，可以用FIR模型描述，其混合滤波器长度为p，矩阵H要求是列满秩的；S＝[S（t），J（t）]T，S（t）是期望的通信信号，J（t）是干扰信号，由于通信信号S（t）和干扰J（t）分别来自不同的发射源，它们是相互独立的，相当于盲信号分离中的源信号；“＊”表示卷积算子，卷积盲分离的目的是从X（t）中获得对源信号的最佳估计，需要寻找一个分离滤波器WT作用在观测信号X（t）上，使得输出信号达到统计独立，即

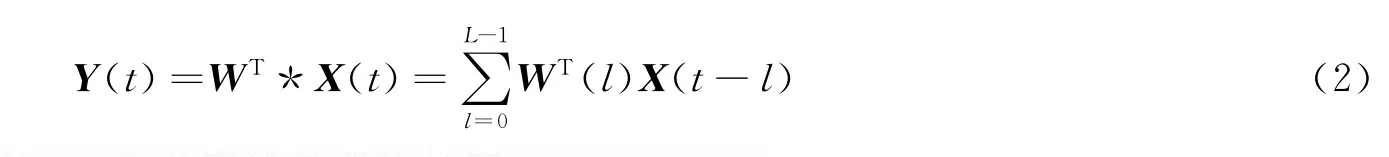
式中Y（t）是源信号的估计；L为分离滤波器的长度。

本文主要研究如何用卷积盲分离方法分离卷积混合的卫星通信信号和干扰的问题，利用傅里叶变换可把时域信号转化成频域信号，时域信号卷积混合形式在频域内可以转化为瞬时混合形式，即：

式中S（w）和X（w）分别是源信号及观测信号的频域表示；H（w）为混合矩阵的频域表示。公式（3）表明时域中卷积盲分离问题可以转化成频域中每个频率点上的瞬时 （但为复数值）盲分离问题，可以采用瞬时盲分离算法来进行分离。

分离模型的频域形式为

式中Y（w）是估计源信号的频域表示。WT（w）的取值必须保证分离出的各个估计源信号的频域形式是互相独立的。

3 卷积盲分离算法及其在卫星接收系统抗干扰中的应用

（1）基于盲分离卫星通信抗干扰系统模型

卫星接收系统中所接收的信号和干扰通过传输通道产生一些卷积混合后，还受到一些加性高斯白噪声（AWGN）的影响，增加了抗干扰的难度。为了实现抗干扰目的，必须设计出合适的卷积盲分离算法对观测信号进行分离，分离出通信信号和干扰，再将有用的通信信号提取出来。基于盲分离卫星接收系统抗干扰系统模型如图1所示。

由于系统中包含有较强的噪声，用普通的独立分量分析（ICA）的方法很难进行分离，针对于此本文提出一种新的对高阶累积量进行联合对角化的卷积盲分离算法。

（2）基于初等反射矩阵的联合对角化的频域算法

白化是解盲分离问题中一种常用且有效的预处理方法[6-7]，对白化后的数据进行ICA往往可以获得更加快速和有效的盲分离算法。对于阵元数大于信源数的情况，白化还降低了混合矩阵的维数，从而减少了待估计参数的个数，降低了计算复杂度。为了利用白化处理的诸多优点，我们将其引入预处理卷积混合数据。通过白化观测信号X（t）来使用信号的二阶信息。在本文中可以使用一个n×m的白化矩阵P来使PX（t）达到白化。定义观测信号X（t）和X（t＋τ）的零时延相关矩阵为

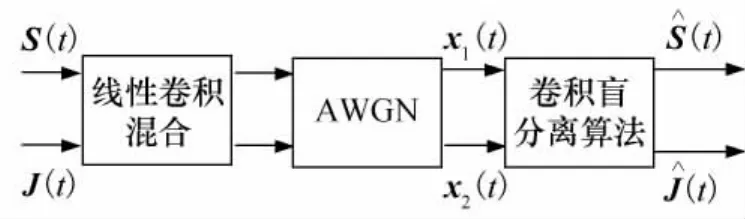
图1 基于盲分离卫星接收系统抗干扰模型Fig.1 System model of satellite communication anti-jamming based on BSS

对Rx（0）进行特征值分解可得

式中U＝[u1，u2，…，um]为特征向量矩阵；Λ＝diag[λ1，λ2，…，λm]为特征值矩阵，且所有的对角线元素以降序排列；（·）H表示Hermitian转置。则白化矩阵P为

对一组高阶累积量矩阵同时进行联合对角化，可以有效地抑制高斯噪声的影响。本文应用高阶累积量中的四阶累积量来进行联合对角化，可以做如下定义。对于任何n×n矩阵M，其四阶累积量矩阵Qx（M）可以定义为

第 （k，l）个累积量片矩阵上的第 （i，j）个索引可以记为Cum（xi，xHj，xk，xHl）。通过使等式M＝bkbHl成立，它也可以被看作等于Qx（M）。其中，bk为一个第k个元素是1，其他元素为0的n×1向量。一个累积量矩阵Qx（M）可以看作是一个以M的索引作为系数的平行累积量片的线性组合[8]。

由于x服从线性模型，累积量矩阵可以转化成一种简单形式。使用累积量的高斯抑制性和附加性等属性可知它也可以表示为

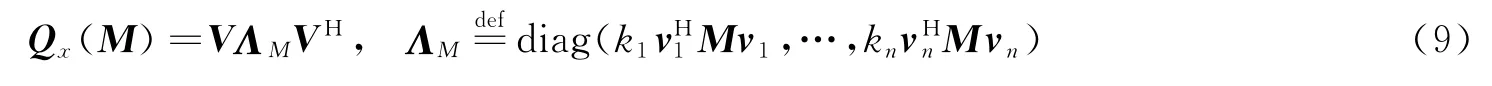
式中V＝[v1，v2，…，vn]为Qx（M）的特征向量矩阵；k1vH1Mv1，…，knvHnMvn表示以升序排列的特征值。公式（9）也说明了关于盲信号处理的基于特征值的一个基本准则：任何累积量矩阵都可以通过U达到对角化。本文就是通过以下方法来使四阶累积量矩阵达到对角化。

令N＝｛Nr｜1≤r≤n｝为一系列n×n矩阵Nr的集合。基于初等反射矩阵对集合N的联合对角化可定义为

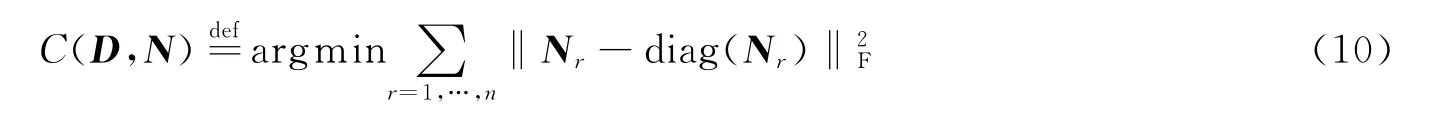
式中 diag（·）是一个矩阵非对角线元素全部为0的算子；‖·‖2F是F-范数的平方。当集合N里只包含一个矩阵时，联合对角化也就等价于常规的矩阵对角化。如果集合N不能被严格地联合对角化（当处理样本累积量时可能会出现这种情况）时，式（10）所表示的最小化准则某种程度上定义了一个 “近似联合对角化”准则。在本文算法中，集合N指的也就是公式（9）中的累积量矩阵Qx（M）的集合。式（10）中D为初等反射矩阵，定义为

式中w是一个2-范数为1的向量，即‖w‖2＝1。利用初等反射矩阵在一个向量中引入零元素，并不局限于转化为单位向量的形式，它可以将向量中任何若干相邻的元素化为零。可以举个简单的例子来介绍一下w的确定，例如，如果要在任意选取的一个向量z＝（z1，…，zn）∈Rn中的从k＋1至j位置引入0元素，只需定义一个向量v：

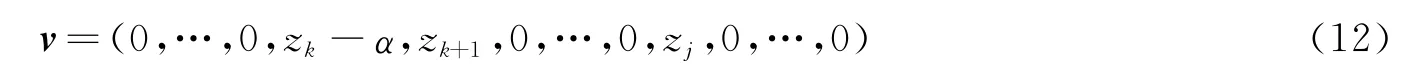
（3）计算复杂度分析比较

G-JBD算法使用平面旋转矩阵来对一系列高阶累积量矩阵进行联合对角化，平面旋转矩阵定义为

式中c＝cosθ，s＝sinθ，用平面旋转矩阵的转置进行左乘产生一个在（i，k）坐标平面的θ弧度的逆时针旋转，经过多次旋转过程即可实现将一系列矩阵进行联合对角化的目的。

如果需要对角化的矩阵阶数为m×n，则G-JBD算法每步迭代中需要估计（mn-1）（mn-2）／2个旋转矩阵，而每个平面旋转矩阵的估计需要求解一元四次（实数情况）或一元六次（复数情况）方程的根，忽略低阶项计算复杂度（CNR）近似为6n＋6mn。而NH-JBD算法每步迭代需估计mn-2个初等反射矩阵，CNR近似为3n＋4mn[9]。因此NH-JBD算法的CNR远小于G-JBD算法的CNR。NH-JBD算法与G-JBD算法的CNR随源信号数目变化曲线图如图2所示。

当源信号数目变大时，两种算法的CNR都越来越大，但NH-JBD算法的CNR变化要比G-JBD算法缓慢得多。说明当源信号数目较大时，NH-JBD算法的CNR要比G-JBD算法的CNR低得多。当用于星上有用信号与干扰信号卷积盲分离时，特别存在多个源时，由于NH-JBD算法要比G-JBD算法的复杂度低，因此NH-JBD算法会更加适合一些。

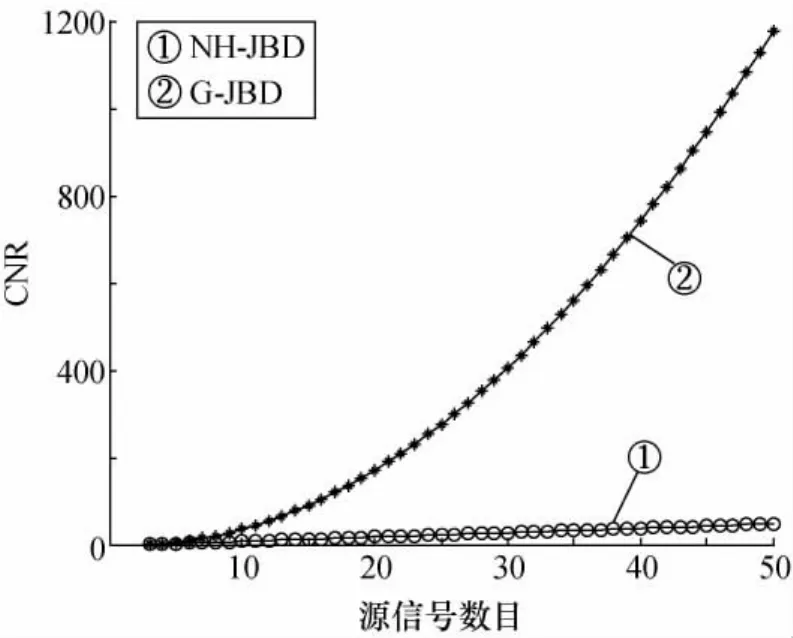
图2 CNR随源信号数目变化曲线Fig.2 Comparison of CNR

4 NH-JBD算法的试验验证

本节通过和G-JBD算法对比仿真来验证NH-JBD算法性能。采用一QPSK信号和一干扰信号的两个源信号波形图如图3所示，上图为QPSK信号，下图为干扰信号。样本点数取50 000。通过卷积混合矩阵来对源信号进行人工混合[10-11]：

混合后信号的个数也设置为2，让它们通过AWGN信道，信噪比设为30dB。混合后信号、通过AWGN信道后的信号及用本文算法对通信信号进行抗干扰处理后的信号分别如图4、5和6所示，图4、5中上图为传感器1接收到的信号，下图为传感器2接收的信号，图6中，上图为QPSK信号，下图为干扰信号。用G-JBD算法分离出的信号波形图如图7所示 （上图为QPSK信号，下图为干扰信号）。

从图7可以看出，试验中除了在幅度上有一定的不同之外，本文算法及G-JBD算法都可以有效地从观测信号中分离出有用通信信号（仿真中为QPSK信号）和干扰信号。为了更直观地评价本文算法的分离效果，计算分离后信号和源信号之间的相似系数[5]：

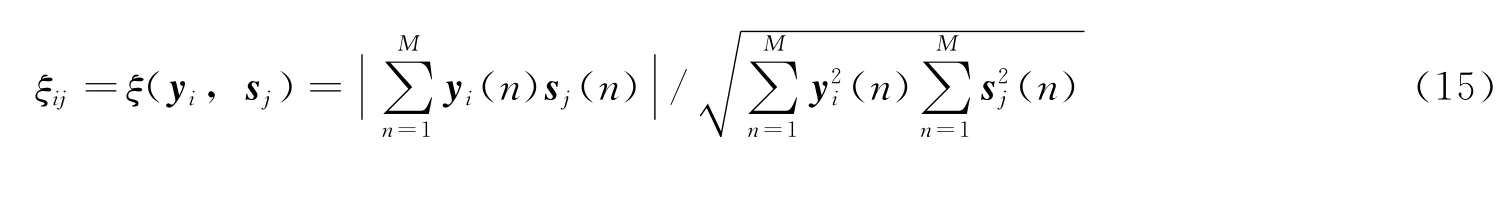
式中sj和yi分别是源信号和估计源信号。如果某一个分离出的信号与某一源信号的相似系数越接近于1，而与其他源信号的相似系数越接近于0，则说明分离的效果越好。试验中两种算法的相似系数ξij比较如表1所示。

图3 源信号波形图Fig.3 Source signals

图5 混合信号通过AGWN通道后波形图Fig.5 Mixed signals of AGWN

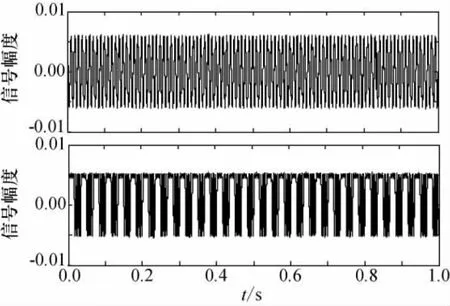
图6 本文算法分离信号波形图Fig.6 Estimated source signals

图7 G-JBD算法分离信号波形图Fig.7 Estimated source signals of G-JBD algorithm

表1 两种算法源信号和估计信号的相似系数比较表Tab.1 Comparable coefficient of the source and the estimated signal

从表1可以看出，NH-JBD算法的相似系数要略大于G-JBD算法的相似系数，说明本文算法的分离性能要优于G-JBD算法的分离性能。

仿真选用的是信噪比为30dB的AWGN信道，通过表1可以看出本算法的分离效果较好，但实际系统中信噪比可能远低于这个值。当信噪比大于10dB时，本文算法对于卷积混合的通信信号和干扰信号的分离仍有较好的分离效果；但当信噪比小于10dB时，本文算法的分离性能将有所下降，但基本也能实现分离。

5 结束语

通过对卷积混叠盲分离算法研究，本文提出了一种新的卷积盲分离算法，该方法使用基于初等反射矩阵的高阶累积量的联合对角化的频域方法来分离卷积混叠盲信号。该算法可以作为一种新的卫星通信抗干扰的方法，应用到卫星通信抗干扰中。由算法过程和仿真试验分析可知，该抗干扰方法可把噪声环境下卷积混叠的有用通信信号和干扰信号分离出来，且有较低的计算复杂度，适合用于星上接收系统的抗干扰中，进而在一定程度上提高卫星通信的抗干扰能力。

[1]SÁNCHEZ V，DAVID A.Frontiers of research in BSS／ICA [J].Neurocomputing，2002，49（5）：7-23.

[3]MANSOUR A，BARROS A K，OHNISHI N.Blind separation of sources：methods，assumptions and application [J].Special Issue on Digital Signal Processing in IEICE Transactions on Fundamentals of Electronics，Communications and Computer Sciences，2000，E83-A（8）：1498-1512.

[4]HAYKIN S.Unsupervised adaptive filtering，vol I：blind source separation [M].New York：Wiley Press，2000，18（6）：21-23.

[5]VRINS F，PHAM D T，VERLEYSEN M.Mixing and nonmixing local minima of the entropy contrast for blind source separatation [J].IEEE Trans.Inf.Theory，2007，15（5）：12-20.

[6]BELOUCHRANI A，ABED-MERAIM K，CARDOSO J F，et al.A blind source separation technique using second-order statistics[J].IEEE Transactions on Signal Processing，1997，45（2）：434-444.

[7]FENG D Z，ZHENG W X，CICHOCKI A.Matrix-group algorithm via improved whitening process for extracting statistically independent sources from array signals[J].IEEE Transactions on Signal Processing，2007，55（3）：962-977.

[8]CARDOSO J F，SOULOUMIAC A.Blind beamforming for nongaussian signals [J].Proc.Inst.Elect.Eng.F，1993，140（8）：362-370.

[9]GOLUB G H，VAN LOAN C F.Matrix computations [M].2nd ed.Baltimore：The John Hopkins University Press，1989：1-46.

[10]MOHAMMED EI RHABI，GUILLAUME GELLE，HASSAN FENNIRI，et al.A penalized mutual information criterion for blind separation of convolutive mixtures[J].Signal Processing，2004，84（2）：1979-1984.

[11]LIU YANHONG，WEI XUEYE，WANG DAHU.A new algorithm for blind source separation of convolutive mixtures[J].Signal Processing，2007，23（12）：801-805.