基于视线测量的卫星编队机动控制方法

张薇 冯孝辉 邓忠民

（1北京航空航天大学宇航学院，北京100191）（2航天东方红卫星有限公司，北京100094）

1 引言

多卫星协同为空间交会、对接、捕获、组装及多方位观测等在轨服务提供更强有力的技术支持，扩展了航天器的功能和技术性能，小卫星编队的应用领域和应用模式不断拓展，在深空探测、科学试验、对地观测和空间控制等领域都将发挥巨大的作用。

国内外已经在小卫星编队方面取得了大量的研究成果。早期的研究多针对简化的主从结构研究编队的保持问题，主从结构队形保持，主星不受控制，从星相对主星进行控制[1-3]。主星由于摄动等在空间发生漂移无法体现，可能造成在队形一定情况下，编队已经偏离任务区域[4]。此外，主星失效势必造成整个编队飞行任务的失败，因此目前的研究重点多集中于无主星的编队控制问题。本文针对空间近距离卫星编队在队形保持基础上的整体转移机动，推导了J2相对摄动力的表达式，建立了一种基于视线测量的无主星链式跟踪协同控制策略，控制方法利用滑模变结构算法实现，控制模型考虑了模型不确定和噪声干扰。建立了整体编队机动的优化模型。仿真算例表明，视线测量协同控制策略能够实现卫星编队构形保持和编队整体转移机动。

2 相对运动分析

参考卫星和主动卫星做近距离相对运动，即两航天器之间的相对距离远小于航天器与地心之间的距离，可以在参考卫星坐标系中建立相对运动方程[5]

由J2引起的地球重力加速度在惯性坐标系里分量为[6]：

由Kepler轨道方程：

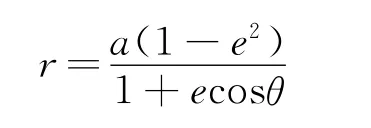
参考卫星在惯性坐标系中的位置坐标为

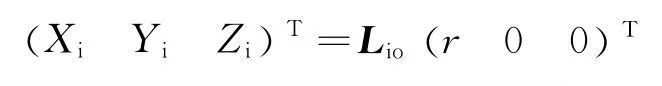
式中Lio为地心轨道坐标系到惯性坐标系的转化矩阵[7]。

用 （xyz）T表示主动卫星在参考卫星轨道坐标系中的位置矢量，那么，它在惯性坐标系中的分量为

式中Lic为轨道坐标系到惯性坐标系的转换矩阵[8]。它们的相对位置引起的摄动力之差（在惯性坐标系中的分量）为

将式（3）转到参考卫星轨道坐标系中有：

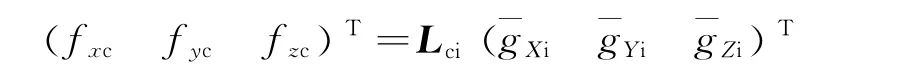
式中Lci是Lic的逆矩阵；fxc，fyc，fzc则为相对位置引起的J2项对卫星的相对摄动力。

3 协同控制器设计

基于上述相对运动分析，建立无主星编队。队形控制采用基于视线测量的循环协同控制方法，即编队每个成员向自己轨道前一成员建立视线测量，如图1所示。假定N（N≥3）个卫星组成的编队，编队卫星Sm跟踪自己最临近的前方编队卫星Sn，S1根据上级控制层指令追踪目标轨道，产生链式编队，那么在t时刻，卫星Sm视线矢量lm（t），（t）可以定义[1]为

其中有N≥3，n＝m-1，m≥2，ρm（t）和（t）为Sm的位置矢量和速度矢量。

编队航天器在机动中的误差可以表示为[8]

式中ld（t），d（t）为参考轨道的位置矢量和速度矢量，而控制系统的目标就是在一定控制时间使em，趋向于0，实现给定的位置跟踪。为了便于控制器的设计，考虑系统不确定性及干扰，式（1）可改写为

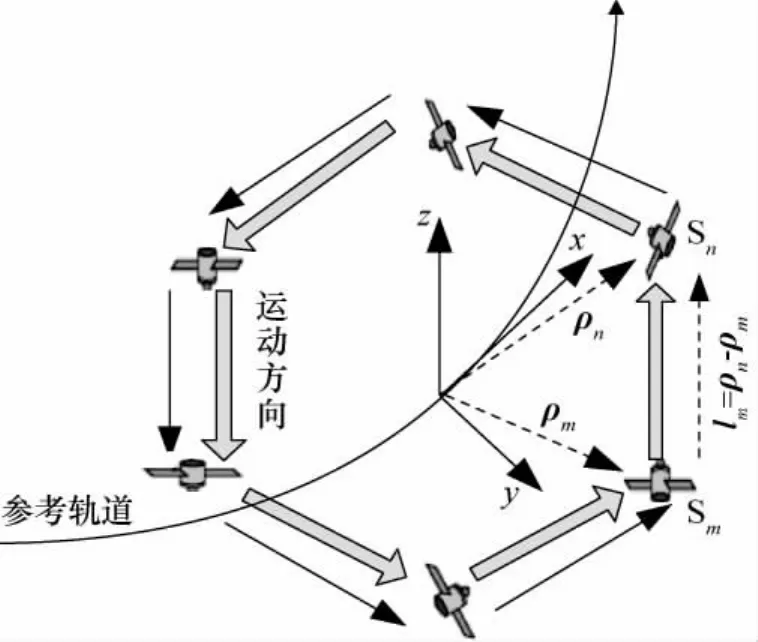
图1 循环编队示意图Fig.1 Chain formation flight

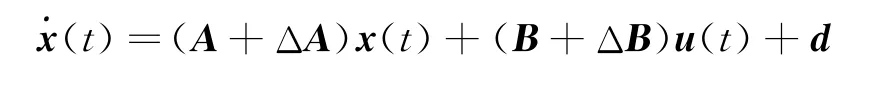
或

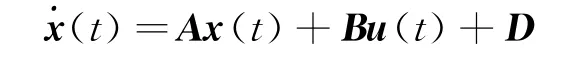
式中x＝[x，y，z，，，]T为系统的状态，输入为扰动项为

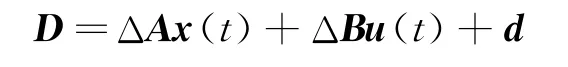
式中 ΔA表示模型参数的不确定性；ΔB表示输入的干扰和不确定性；d代表任意匹配的摄动。D满足系统的匹配条件，‖D‖≤δ，2δ认为是干扰的界限。

滑模控制的滑模面设计[9]为

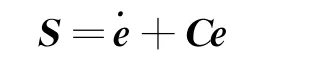
式中S＝[s1，s2，s3]T；C＝diag（c1，c2，c3），为滑模控制参数。

设计滑模系统的趋近律为

式中K＝diag（k1，k2，k3）是控制增益矩阵，k1，k2，k3为常数，ki＞ δ，i＝1，2，3。因此系统的输入可以得到：

符号函数sgn（S）为

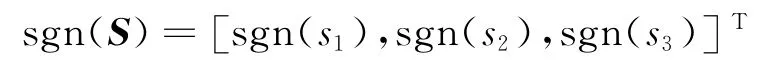
利用李雅普诺夫函数对控制系统进行稳定性分析，系统的函数可以记为

所以有：

因此，系统是渐进稳定的。

为减少系统的抖振，对系统进行如下转化：

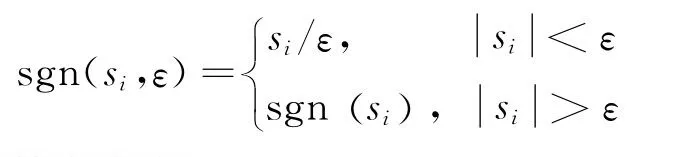
其中ε为常数，因此系统的输入变为

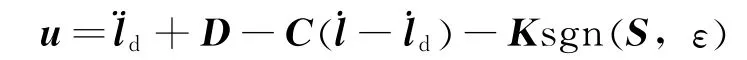
4 优化模型

滑模变结构控制的控制效果与控制器的滑模面选取，趋近率和边界层宽度有很大的关系。c越大，滑模运动段相应越快，系统快速性越好，但过大的c值都将使控制量过大，实际中会引起抖振，设置整体编队机动的优化模型为

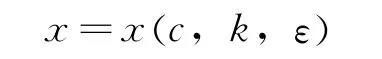
优化目标函数：

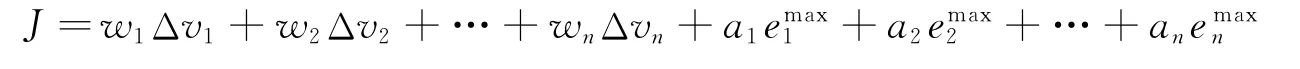
式中w1，w2，…，wn为编队成员卫星燃料消耗的加权项；a1，a2，…，an为编队成员卫星最大位置误差的加权项。

机动优化的约束条件：

1）优化变量的取值约束：

2）机动结束后的位置约束条件：

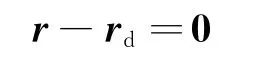
式中r为编队成员卫星在轨道坐标系下的矢径；rd为编队成员卫星机动的目标矢径。

5 算例分析

利用精度较高的相对轨道要素法，建立基于参考轨道的无主星三星圆形编队，编队参考轨道的轨道要素为：a＝7 300km，e＝0．01，i＝30°，Ω＝0°，ω＝0°，M＝45°。

在仿真中，采用非线性动力学模型公式（1），考虑摄动影响，J2摄动和随机白噪声干扰。使用了上文提供的协同控制方案以及基于非线性模型的低端滑模控制器，编队卫星在参考卫星轨道坐标系下的初始位置与速度如表1所示。

1）队形整体机动仿真。在某时刻，假设S1卫星接收地面指令或更高级控制层命令，编队绕飞中心从参考卫星轨道坐标系中心改为（1，10，1）km，编队整体执行变轨，最终实现对期望轨道的跟踪，S2跟踪S1，S3跟踪S2，通过视线测量信息，自主地完成队形控制，控制参数设置为ε＝0．001，C＝diag[4×10-5，4×10-5，4×10-5]，K＝diag[7．6×10-5，7．6×10-5，7．6×10-5]，仿真结果如图2所示。编队整体机动过程中的星间距离如图3所示。

表1 编队卫星初始状态Tab.1 Initial status of formation satellites m

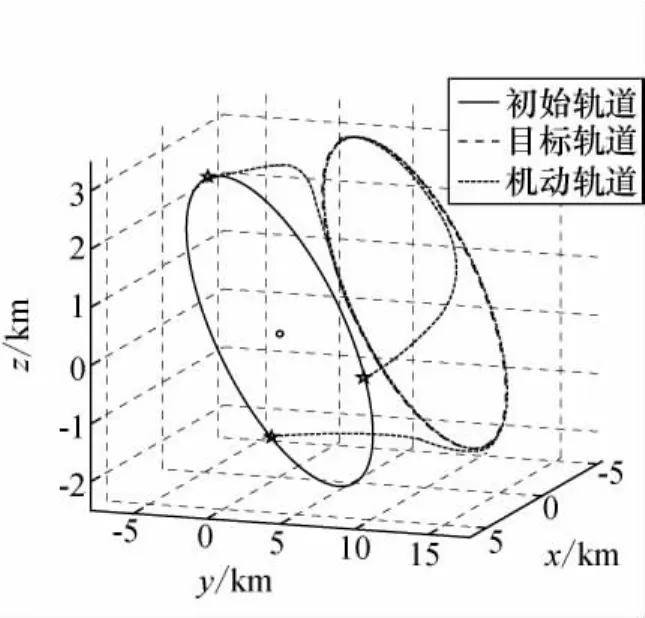
图2 链式编队队形整体机动Fig.2 Chain formation maneuver

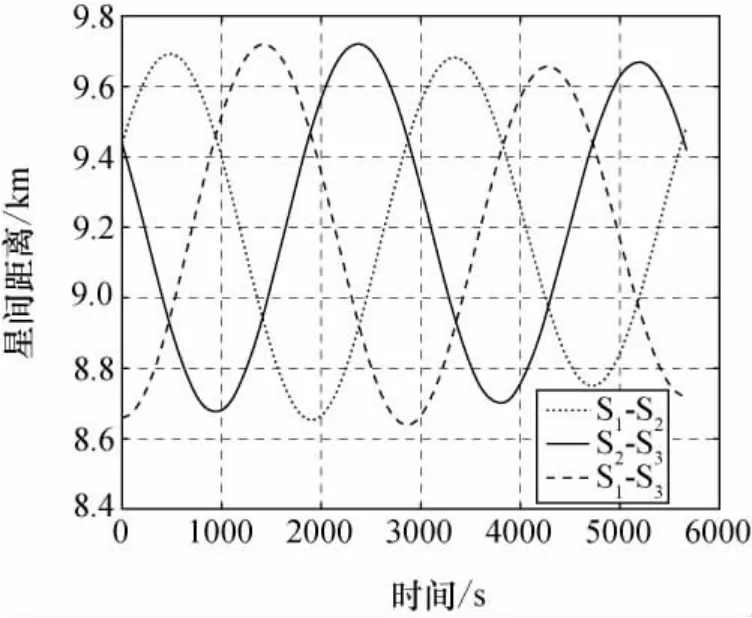
图3 编队整体机动过程中的星间距离Fig.3 Distance between satellites during formation whole maneuver

2）优化机动仿真。趋近率参数k、边界层参数ε与滑模面参数c的确定，往往受到多个相互制约因素的影响。为了得到较好的系统性能，运用遗传算法（Genetic Algorithms，GA）来优化和确定这些参数，在相互矛盾的约束条件下，取得最佳的控制效果。基于前面给出的优化模型，初始条件采用表1中的卫星编队初始条件，设计编队为三星低轨道圆形编队，优化目标的权值取为1、1、1，0、0、0，即优化目标为编队机动整体燃料消耗最少，优化变量ε，c，k的取值范围分别为[2×10-5，4×10-3]，[1×10-6，7.6×10-5]，[1×10-3，1×10-4]，利用遗传算法进行优化分析求解，可以得到如下的仿真结果：图4给出了整体燃料消耗最少的编队机动轨迹；图5给出了遗传算法寻优结果，平均适应度为0.645 39，最佳适应度为0.343 7；图6给出了编队机动过程中的星间距，可以看出在优化机动下编队整体机动星间相对距离保持在8.5km之上，满足相关的工程需求。

表2列出了上文两种机动方法下的卫星燃料消耗，并与参考文献[9]进行了对比，可以看出，无主星协同与有主星协同的燃料消耗基本相当，在本文的燃料最优的机动目标下，编队整体机动的燃料消耗少了，但机动的误差有所增加。

表2 编队机动燃料消耗和误差Tab.2 Fuel cost and error during formation maneuver

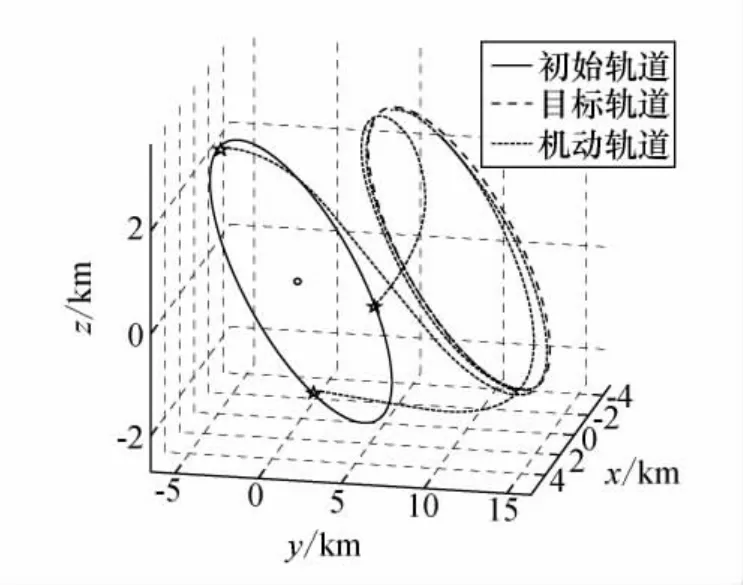
图4 编队机动优化结果Fig.4 Formation maneuver optimization

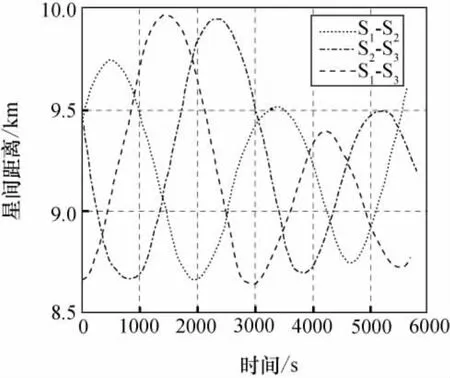
图6 编队机动过程中的星间距离Fig.6 Distance between satellites during formation maneuver

6 结束语

本文提出了一种视线测量链式无主星卫星编队协同控制方法，通过队形保持机动和编队整体机动控制的仿真分析，可以得出如下结论：

1）相对主从结构队形保持，本文提出的视线测量链式无主星编队各个卫星都受控，能够保证编队长时间服务在任务区域；

2）视线测量链式无主星编队，有利于编队各卫星自主性的发挥，能够更好地满足空间任务需要，实现自主、灵活的卫星编队机动。

[1]PINI GURFIL.Cyclic spacecraft formations：relative motion control using line-of-sight measurements only[J].Journal of Guidance，Control and Dynamics，2007，30（1）：214-235.

[2]SCHAUB HANSPETER，VADALI SRINIVAS，JUNKINS JOHN，et al.Spacecraft formation flying control using mean orbit elements[J].Journal of the Astronautical Sciences.2000，48（1）：69-87.

[3]IGOR BEIGILMAN PINI GUR.Graph-theory-based optimal impulsive formation keeping [J].AIAA Guidance，Navigation and Control Conference and Exhibit，Hilton Head，South Carolina，2007.

[4]孟云鹤，贺勇军，戴金海.卫星编队的多冲量轨道机动路径规划方法 [J].宇航学报，2005，26（4）：491-495.MENG YUNHE，HE YONGJUN，DAI JINHAI.Path planning for satellite formation′s multi-impulse orbit maneuvers [J].Journal of Astronautics，2005，26 （4）：491-495.

[5]KOJI YAMANAKA，FINN ANKERSEN.A new state transition matrix for relative motion on an arbitrary elliptical orbit[J].Journal of Guidance，Control and Dynamics，2002，25（1）：60-66.

[6]MISHNE DAVID.Formation control of satellites subject to drag variations andJ2perturbations [J].Journal of Guidance，Control and Dynamics，2004，27（4）：685-692.

[7]肖业伦.航天器飞行动力学原理 [M].北京：宇航出版社，1995：101-103.XIAO YELUN.Spacecraft flight dynamics theory [M].Beijing：Astronautic Publishing House，1995：101-103.

[8]YEH HSIHAN，NELSON ERIC，SPARKS ANDREW.Nonlinear tracking control for satellite formations[J].Journal of Guidance，Control and Dynamics，2002，25（2）：376-386.

[9]LIU HUI，LI JUNFENG，BAOYIN HEXI.Sliding mode control for low-thrust earth-orbiting spacecraft formation transferring [J].Aerospace Science and Technology，2006，10（7）：636-643.