自动装填系统协调器结构静力学及动力学研究

冯广斌,王浩亦,孙华刚,朱汗青

(1.军械技术研究所，河北 石家庄 050003；2.军械工程学院，河北 石家庄 050003)

自动装填是自行火炮的发展趋势之一[1]。协调器是某自行火炮自动装填系统中的一个子系统，主要负责从供弹仓接受弹丸并将其协调到与炮管轴线平行的位置。南京理工大学的侯保林教授在文献[2]中对协调器的结构与控制的综合设计方法进行了研究，并确定了支臂的截面尺寸；军械工程学院的李伟在文献[3]建立了协调器的虚拟样机模型，分析了小平横机气压和液量两种故障因素的影响。本文在继承前人工作的基础上，拟利用ANSYS软件对协调器进行有限元分析，掌握协调器的静力学和动力学分析结果。

1 工作原理及有限元模型

协调器的工作原理如图1所示。协调器在接受了供弹机的弹丸后，支臂绕右耳轴转动，带动弹丸旋转至与炮管轴线平行的位置，由输弹机完成推弹入膛的动作[4]。

在ANSYS的通用前处理模块(Pre7)中，建立了协调器的三维简化模型，忽略相应的倒角、圆角及不重要的细小结构。简化后的协调器模型主要由支臂、底端盖、活塞杆、缸筒和弹丸组成。

根据各部分的形状特点，支臂采用8节点六面体单元扫略分网，其余部分采用10节点四面体单元自由分网。在活塞杆和销轴的接触面、销轴和支臂的接触面附近细化网格，以达到精确结果的目的。分网结束后共得到16 183个单元和31 387个节点。定义材料密度ρ=7 800 kg/m3，杨氏模量E=2×105MPa，泊松比μ=0.3。

根据协调器的拓补关系[3]，给模型添加相应的约束：选取底端盖相应的面，约束住其3个方向的自由度；选取缸头上相应的面，将面上节点的节点坐标系旋转至柱坐标系下，约束住X和Z方向的自由度，以模拟旋转铰约束；在活塞杆与缸筒之间、杆头与销轴之间以及销轴与支臂之间添加接触对。建立好的协调器有限元模型如图2所示。

2 协调器静力学分析

在对协调器进行动力学分析之前，有必要先对其进行静力学分析，以便从整体上掌握协调器的受力情况，确定危险点位置。

活塞杆受到的油缸压力[5]：

(1)

式中:p0和S分别为蓄能器的初始压力和油缸活塞面积；V0为气体初始容积；n为蓄能器的多变指数；ΔV为气体容积变化量，初始位置时取值为0。由式(1)可以计算出在任一位置时活塞杆受到的油缸压力。

选取支臂相应的节点添加质量单元MASS21，以模拟托弹盘和弹丸的质量。添加重力加速度和油缸压力，便可以进行静力学求解。

分别计算支臂在转至0°、30°和60°静止时的有限元模型。经分析，可得如下结论：

1)协调器支臂在0°、30°和60°位置时的最大变形量分别为0.167 9、0.180 5和0.121 1 mm，最大等效应力分别为35.83、36.34和24.95 MPa，虽然最大变形量和最大应力均符合要求[6]，但容易看出其变化趋势不是单调的，有必要对其变化趋势进行研究；

2)发生最大变形量的位置为支臂的末端，发生最大应力的位置为平衡机与支臂的铰接处附近，这为确定协调器在工作过程中发生最大变形量位置和最大应力位置提供了理论依据，对瞬态动力学中明确分析重点很有指导意义。

3 协调器结构动力学分析

在对协调器进行了静力学分析之后，为了更好地模拟协调器的真实工作状况，有必要对协调器进行动力学的分析。

3.1 模态分析

模态分析是其他动力学分析的基础[7]，通过模态分析，可以首先掌握协调器的固有频率和主振型。

协调器的主要作用是将弹丸协调至与炮膛轴线一致的方向，所以如果支臂自身变形，将引起弹丸定位不准确，进而影响下一步的输弹动作。火炮在完成一枚炮弹的发射之后，车体会在一段时间内存在余振，所以，有必要对协调器进行模态分析，以掌握其固有频率和主振型。

在模态分析中，考虑到主要是低阶模态对协调器的影响较大，所以只需要求出前几阶模态就可以满足分析要求[8]。采用ANSYS 软件模态分析中的Lanczos法对协调器模型进行了有限元模态分析，得到了其各阶固有频率和相应的固有振型。表1列出了协调器的前8阶固有频率和振型特征。

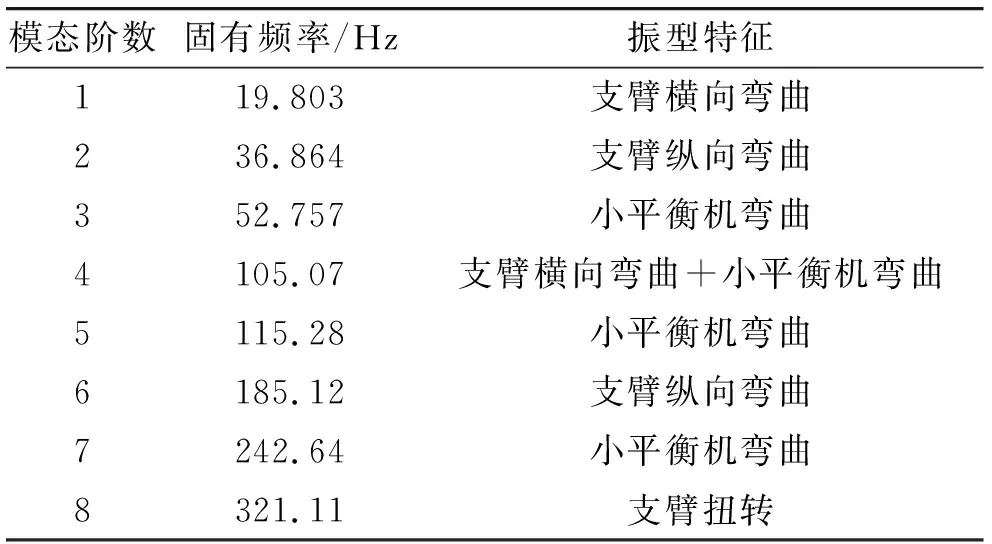
表1 协调器前8阶固有频率及振型特征

通过表1可以得知协调器的主要变形为支臂弯曲变形和小平衡机弯曲变形。其中尤以支臂的弯曲变形对输弹动作的 影响最大。分析结果直观地显示出支臂和平衡机耦合振动的变形特征。

3.2 瞬态动力学分析

协调器的静力学分析只能研究协调器静止在某一位置时的应力应变情况，而不能计算协调器因旋转产生的向心力的影响。因而有必要对其工作过程进行瞬态动力学分析。对协调器进行瞬态动力学分析有以下优势：

1)可以考虑惯性力的影响，增加仿真结果的可信度。

2)能够得到协调器在任一时刻、任一位置的受力变形情况，从而掌握协调器工作全过程的工作状态。

3)容易获得重要参数随时间的变化曲线。

3.2.1 协调器工作过程的近似模拟

协调器在工作过程中主要受到重力、向心力、切向力以及活塞杆与支臂之间作用力的影响。由于协调器的位置随时发生变化，所以各作用力产生的影响也随之改变。为了在ANSYS中最大程度地模拟协调器的受力状况，需要掌握各作用力的变化规律和作用方式，明确作用力的添加方法。

图3是协调器支臂旋转至任意位置φ时的受力简图。根据该受力简图，需要在ANSYS中为支臂添加重力、向心力、切向力以及与活塞杆的接触力。由于ANSYS软件的局限性，本文采用近似的处理方法：将坐标系r-t建立在支臂上，这样可以认为协调臂静止不动。然后在选取相应位置添加各作用力，且各力的大小和方向按真实规律变化，以便最大限度地模拟支臂的真实工况。

本文主要对协调器目标值为20°、40°和60°三种情况下的有限元模型进行了研究，摆弹时间均为1.2 s。

1)小平衡机力学模型及重力的近似施加。

由文献[2]可知支臂转角φ的变化规律。如图3所示，由余弦定理，计算任意位置的小平衡机长度：

(2)

又知：

ΔV=SΔc=S[c(0)-c(t)]

(3)

将(1)、(2)、(3)三式联立，便可求得平衡机对支臂支撑力F的大小。

协调器支臂在转动过程中，不仅平衡机力F的大小变化，其方向也是不断变化的。为了模拟其方向的改变，将F分解成沿x轴方向的力Fx和沿y轴方向的力Fy。通过设置Fx、Fy的变化规律，可以使其合力按照F的规律变化。

如图3所示，再次根据余弦定理，可知：

α(t)=arccos[(a2+c(t)2-b2)/2ac(t)]

(4)

显然有：

θ(t)=α(t)-φ(t)

(5)

将(1)、(4)、(5)式带入下列两式，便可求得平衡机力分量Fx和Fy的大小。

Fx=Fcos[θ(t)]

(6)

Fy=Fsin[θ(t)]

(7)

同理，如果将协调器支臂看作静止不动，协调器重力的方向将随时间而改变。由于支臂本身为一薄壁结构，自身重力影响很小，故可忽略支臂本身的重力。将托弹盘和弹丸的重力分解到r轴和t轴两个方向，容易得到：

Gr=Gsinφ

(8)

Gt=Gcosφ

(9)

如表2～表4所示，在支臂目标值为20°、40°和60°三种情况下，分别从φ(t)曲线中等距选取11个数值点，利用(1)～(9)式，可以计算出各数值点对应的Fx、Fy、Gr和Gt值。

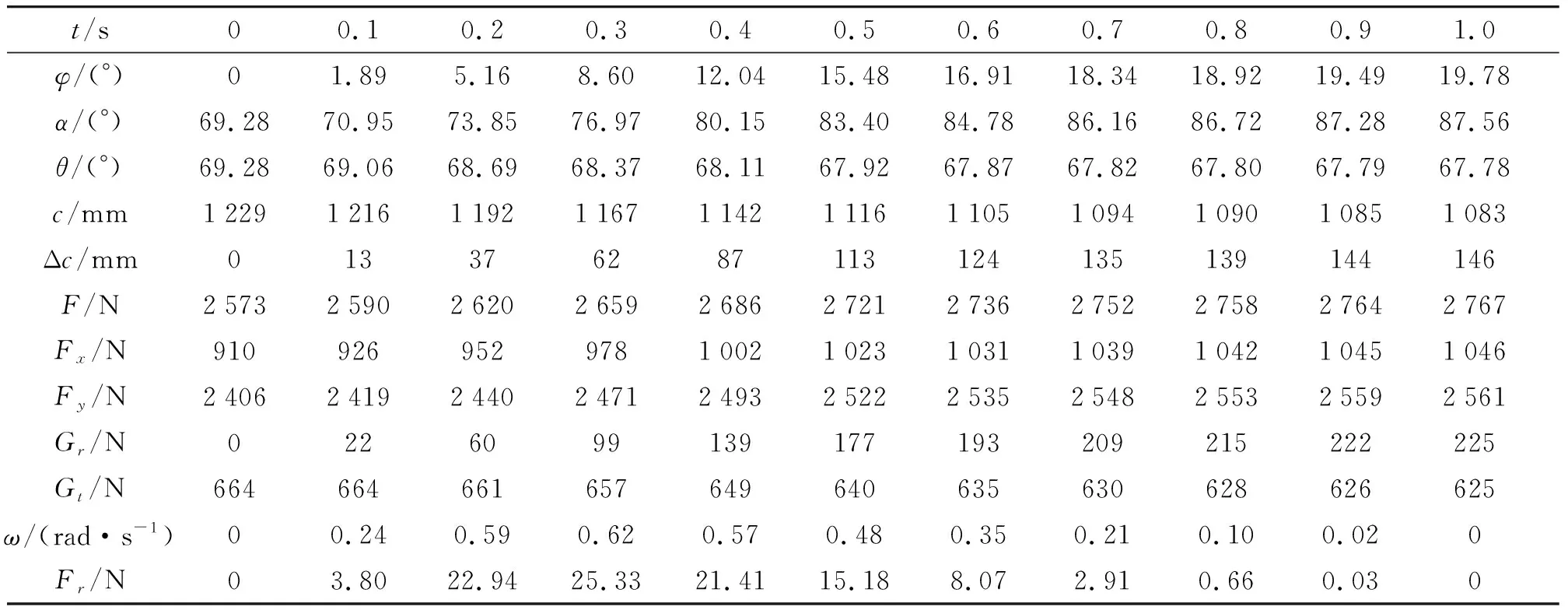
表2 平衡机力、重力及惯性力计算数值表(目标值为20°)

表3 平衡机力、重力及惯性力计算数值表( 目标值为40°)

表4 平衡机力、重力及惯性力计算数值表(目标值为60°)

在得到各组Fx、Fy、Gr和Gt值之后，利用曲线拟合求出Fx(t)、Fy(t)、Gr(t)和Gt(t)函数。在ANSYS中选取作用力添加点，便可以将各作用力以函数的形式添加到模型中。

2)惯性力Fr、Ft的近似施加。

协调器支臂在转至某一角度的过程中，会经历一个先加速后减速的过程。在这期间会产生惯性力的影响。而在静态分析中，由于只能对某一静止状态进行研究，无法计及惯性力的影响，所以需要在瞬态动力分析中加以完善。

同样，如表2～表4所示，协调器惯性力的添加也采用了近似施加的方法：同样忽略支臂的惯性力，在支臂转速曲线ω(t)上选取一组数值点，由向心力公式：

Fr(t)=mω2r

(10)

可计算出模型受到的向心力。其中，m为托弹盘和弹丸的质量；r为其质心距离协调器右耳轴的长度。利用曲线拟合可得向心力函数Fr(t)。

对ω(t)函数取导可得支臂角加速度函数β(t)。由切向力公式:

Ft(t)=mβ(t)r

(11)

可计算托弹盘和弹丸在旋转过程中产生的切向力。

3.2.2 协调器支臂的瞬态动力学分析

在对协调器模型施加完作用力之后，设定好时间步长、输出控制选项，便可以对其进行瞬态动力学求解。

3.2.2.1 通用后处理器(POST1)

求解结束后，利用ANSYS中的通用后处理器可以查看支臂某一时刻的位移和应力云图。

在0.7 s时，目标值为20°时的协调器最大位移为0.106 0 mm，最大应力为27.39 MPa；目标值为40°时的最大位移为0.165 2 mm，最大应力为28.24 MPa；目标值为60°时的最大位移为0.101 6 mm，最大应力为27.42 MPa。由此可得：

1)支臂的最大位移和最大应力均在合理的范围之内，在0.7 s时支臂的工作状态符合材料的刚强度要求。

2)瞬态动力学分析的结果与静力分析的结果较为接近，验证了两种分析结果的正确性。

3)目标值为不同值时同一工作时刻的支臂的位移和应力虽然相差不大，但也不完全相同。这说明目标值的不同会对支臂的工作状态造成一定影响，这对实际使用很有指导意义。

3.2.2.2 时间后处理器(POST26)

利用时间后处理器可以查看模型的某一变量与时间的函数关系[9]。

观察各时间节点的位移云图和应力云图，可以发现最大变形出现在支臂的边缘处，而肋板与支臂交界处的应力一般较大。选取支臂最边缘的节点252 184和肋板与支臂交界处的节点62 050，将支臂在节点252 184的Y向位移和节点62050的等效应力定义为变量，绘制出的位移—时间曲线和应力—时间曲线如图4和图5所示。

从以上仿真结果可以得到如下结论：

1)3种目标值下协调器支臂在节点252184处的变形在0.15 mm以内，节点62050处的应力在25 MPa以内，最大变形和最大应力均在许用范围之内，可见协调器的设计是符合要求的。

2)不同目标值下的变形变化曲线和应力变化曲线虽然变化趋势相差不大，但却都不尽相同。这主要是因为目标值不同，同一时刻协调器的转角、转速和角加速度也不同，从而导致重力的分量和受到的惯性力存在差别，故其变化趋势不完全相同。分析结果为掌握协调器在工作过程中的工作状态、确定危险时刻和支臂的优化设计等提供了理论依据。

4 结束语

本文利用有限元技术建立了协调器的有限元模型，并根据工作条件对其进行了静态、模态和瞬态动力学的分析。通过研究掌握了协调器的基本工况，其变形和应力结果对协调器的设计和维修保障很有借鉴意义。

[1] 李伟.供输弹系统机电液耦合动力学及动力可靠性仿真研究[D].石家庄：军械工程学院，2010.

LI Wei. Simulation research on mechanical-electrical-hydraulic coupling dynamics and action reliability of ramming system[D]. Shijiazhuang：Ordnance Engineering College，2010.(in Chinese)

[2] 侯保林.弹丸传输臂结构与控制的综合设计方法[J].兵工学报，2006，27(5): 50-52.

HOU Bao-lin. Integration design method of structure and control for a shell transfer arm[J]. Acta Armamentarii，2006，27(5): 50-52. (in Chinese)

[3] 李伟.协调器故障仿真及应用研究[J].火炮发射与控制学报，2009(3): 36-39.

LI Wei. Study on fault simulation and application of coordinator[J]. Journal of Gun Launch & Control，2009(3): 36-39. (in Chinese)

[4] 周宁.ANSYS机械工程应用实例[M]. 北京：中国水利水电出版社，2006.

ZHOU Ning. ANSYS mechanical engineering application examples[M]. Beijing: Water Conservancy and Hydropower Press of China，2006. (in Chinese)

[5] 侯保林.火炮自动装填[M].北京：兵器工业出版社，2010.

HOU Bao-lin. Automatic loading of artillery[M]. Beijing: The Publishing House of Ordnance Industry，2010. (in Chinese)

[6] 张培林，李国璋，傅建平.自行火炮火力系统[M].北京：兵器工业出版社，2002.

ZHANG Pei-lin，LI Guo-zhang，FU Jian-ping. Fire system of self-propelled artillery[M].Beijing: The Publishing House of Ordnance Industry，2002. (in Chinese)

[7] 涂振飞.ANSYS有限元分析工程应用实例教程[M].北京：中国建筑工业出版社，2010.

TU Zhen-fei. Engineering application examples tutorial of ANSYS finite element analysis[M]. Beijing:Building Industry Press of China，2010. (in Chinese)

[8] 胡君君.VMC-1000主轴箱模态分析及改进设计[J].机械设计与制造，2011(1): 50-52.

HU Jun-jun. Modal analysis and modification design of the VMC-1000 spindle box[J]. Machinery Design & Manufacture，2011(1): 50-52. (in Chinese)

[9] 丁毓峰.ANSYS有限元分析完全手册[M].北京：电子工业出版社，2011.

DING Yu-feng. Complete manual of ANSYS finite element analysis[M].Beijing: Publishing House of Electronics Industry，2011. (in Chinese)