近炸射击高炮系统的点射毁伤概率

陶德进，王 军，张 捷，凌满蓉，薄煜明

(1.南京理工大学，江苏 南京 210094; 2.重庆望江工业有限公司，重庆 400071)

毁伤概率是武器系统最重要的性能指标之一。对近炸射击高炮系统，国军标给出了一次齐射毁伤概率的蒙特卡罗算法[1]。中小口径高炮系统主要以点射方式拦截空中目标，这类武器系统的射频很高，点射中不同时刻的射击误差之间具有较强的相关性，不能由一次齐射的毁伤概率计算点射毁伤概率。

现有文献多是基于误差模型转换法计算近炸射击高炮系统的点射毁伤概率[2-3]。所谓误差模型转换法，其实质是将弱相关误差分解出强相关误差部分和不相关误差部分，进而将射击误差分为重复误差分量和不重复误差分量，这种分解本身存在着未知程度的近似。也有文献提出基于折合域的点射毁伤概率计算方法[4]，这种方法一定程度上减少了计算量，但同样存在未知程度的近似。 本文提供了近炸射击高炮系统点射毁伤概率的蒙特卡罗算法，它不存在误差模型转换法的近似。其计算过程如下：随机生成点射的射击诸元误差分量、射弹散布和起爆角，计算射击误差，进而计算毁伤概率。

1 射击诸元误差分析

近炸射击高炮系统的射击误差分析涉及如下3个坐标系：Z坐标系、Xh坐标系和X坐标系，3个坐标系如图1所示，各自定义如下：

1)Z坐标系。原点为目标提前点Mq；Z1轴与提前水平距离方向相一致；Z2轴垂直于水平面，指向上方；Z3轴垂直于射面，指向目标前进的方向。

2)Xh坐标系。原点为Mq；Xh3轴平行于计算弹道在Mq点的切线，与射弹运动速度v的方向相反；Xh1轴在目标航路L与Xh3轴构成的平面上，垂直于Xh3轴，指向目标前进的方向；Xh2轴垂直于Xh1轴和Xh3轴，指向上方。

3)X坐标系。原点为Mq；X1轴为相对速度vxd(射弹相对目标的速度)法平面与相对射面(过vxd的铅垂面)的交线，指向上方；X2轴在vxd的法平面内，与X1轴垂直，指向目标前进的方向；X3轴与vxd方向相反。

近炸射击高炮系统的射击误差由弹着点误差和起爆角两部分引起，而弹着点误差由射击诸元误差和射弹散布引起。在Xh坐标系内，记1门单管高炮n发点射中第k个射击误差为x(k)，则：

x(k)=fk[a,xq(k)，xr(k)，xb(k)，φb(k)]

(1)

式中：a、xq(k)、xr(k)分别为射击诸元误差的常数分量、强相关分量和弱相关分量，三者均为二维向量，包括高低角误差和方位角误差两个分量；xb(k)为射弹散布，亦为二维向量；φb(k)为起爆角；fk为时变的映射函数。

事实上，射击诸元误差可进一步分解，其中，xq(k)包括气象测量误差、初速准备误差分别引起的射击诸元误差xq1(k)、xq2(k)；xr(k)包括跟踪系统、解算系统、随动系统和稳定系统(自行炮配有)分别引起的射击诸元误差xr1(k)、xr2(k)、xr3(k)和xr4(k)。 由上述分析，有:

x(k)=fk[a,xq1(k),xq2(k),xr1(k),xr2(k),

xr3(k),xr4(k),xb(k),φb(k)]

(2)

起爆角φb服从反射正态分布，其概率密度函数为：

(3)

式中：φb0为理论起爆角。

本文的蒙特卡罗算法基于如下假定：a、φb0、σφb已知；在所有点射中，xq1(k)、xq2(k)呈方差已知的正态分布；在同一点射中，xq1(k)、xq2(k)保持不变，xr1(k)、xr2(k)、xr3(k)、xr4(k)为方差和相关系数均已知的零均值平稳正态序列，xb(k)为方差已知的零均值平稳正态序列。对处在研制阶段的武器系统，各参数可由设计指标确定；对已研制成功的武器系统，各参数可在定型试验中确定。 对射击诸元误差分量的重复性分析需结合武器系统的组织结构进行[5]。高炮系统的组织结构如图2所示。

图2中，指挥仪中包含了解算系统。解算系统根据跟踪系统(雷达、摄像机等)提供的目标位置参数，求解出目标提前点位置Mq，并解算出标准气象和弹道条件下射击诸元。指挥仪根据气象测量装置给出的气象条件和初速准备装置给出的弹药初速对解算出的射击诸元进行修正，给出最终的射击诸元。

对射击诸元误差的重复性分析是基于如下事实：同一数据处理设备在同一时刻对某组数据的处理结果是唯一的。

图2所示的高炮系统中，若有l台指挥仪，每台指挥仪带m门火炮，每门火炮有p个身管(非转管炮)。则武器系统一次齐射产生的lm个射击诸元误差中的重复分量有xq1、xr1；每台指挥仪给出的m个射击诸元的误差重复分量除xq1、xr1外，还有xr2。

结合射击诸元误差分量的相关性分析可知，对该武器系统的点射过程进行随机模拟时，需生成的随机项包括：1个xq1、lm个xq2、n个xr1、ln个xr2，lmn个xr3，lmn个xr4，lmpn个xb。当武器系统中包含不止一个跟踪子系统时，可类似分析。

2 蒙特卡罗法

2.1 随机误差的生成

考虑一维情况[6]：

(4)

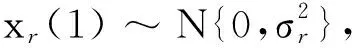
对概率密度函数为 (3) 式的随机数，取uφb～N{0,1}，则φb=|uφbσφb|+φb0为符合条件的随机起爆角。

2.2 射击误差计算

近炸射击的射击诸元误差包含如下互不相关的两项：方位角误差Δβ和高低角误差Δα。其中，Δβ引起的弹着点误差沿Z3轴方向，正向同Z3轴正向，记Z为此方向的单位向量；Δα引起的弹着点误差沿提前炮目垂直面与射面的交线方向，正向朝上，记N为此方向的单位向量。Z和N在Xh坐标系中的坐标分别为[1]：

(5)

在随机生成点射的射击诸元误差、射弹散布和起爆角后，可结合式(5) 计算弹着点误差在Xh坐标系中的坐标 (xhp1，xhp2，xhp3) ，进而计算射击误差(xh1，xh2，xh3)。

事实上，射弹并未运动到弹着点，在其运动到自身速度v的方向 (Xh3轴的反方向) 与弹目连线夹角为φb时即发生爆炸，炸点在Xh坐标系中的坐标即为射击误差。可按下式计算射击误差在Xh坐标系中的坐标[1]：

(6)

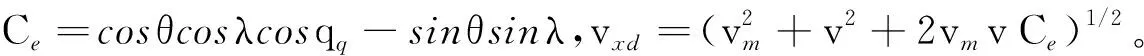
2.3 毁伤概率计算

在一次点射的射击误差生成之后，即可计算此次点射的毁伤概率。重复试验，求取均值，即为武器系统的点射毁伤概率。

对坐标毁伤定律，在获取射击误差之后，根据目标和弹丸的飞行参数、弹药的爆炸特性等，可以解破片与目标的命中问题，进而求取毁伤概率。另有一种近似方法[7]：对编号为s的一次点射模拟中，射击误差为x(i,j,k)的弹药对目标的毁伤概率为：

(7)

(8)

若一共进行了t次模拟，则武器系统的点射毁伤概率为：

(9)

2.4 与现有算法的对比

现有算法都是基于误差模型转换法的毁伤概率算法，其实质是将弱相关误差分解为两部分，一部分与强相关误差合并为武器系统的重复误差，另一部分与不相关误差合并为武器系统的不重复误差。

对图2所示的高炮系统，以l=1为例：m=1，n=1时，xr1(k)、xr2(k)、xr3(k)、xr4(k)全部合并到重复误差；m=1，n>1时，xr1(k)、xr2(k)、xr3(k)、xr4(k)全部进行分解；m>1，n=1时，xr1(k)、xr2(k)合并到重复误差，xr3(k)、xr4(k)合并到不重复误差；m>1，n>1时，xr1(k)、xr2(k)进行分解，xr3(k)、xr4(k)合并到不重复误差。

上述4类情形中，m>1时，将xr3(k)、xr4(k)合并到武器系统的不重复误差是一种近似处理，这种处理忽略了xr3(k)、xr4(k)的相关性，若还有p>1，则上述处理在重复性的分析上也存在近似。对弱相关误差分则是在上述近似的基础上又进行了一次近似。

蒙特卡罗算法不存在上述各种近似，因而可用于评价现有的各种算法。蒙特卡罗算法与现有算法相比的缺点在于计算时间较长，以现有的计算水平，其计算时耗是可以承受的。

现给出蒙特卡罗算法与现有算法的对比分析实例。一台指挥仪指挥两门双管炮的高炮系统，对目标进行各管5发的点射。给定目标航路条件：水平匀速飞行，航速vm=250 m/s，高度H=2 000 m，航路捷径dj=1 000 m。在航路捷径前，斜距离Dq=3 000 m处开始射击。并已知：

1) 系统误差。 高低角：2 mil；方位角：2 mil。

2) 射击诸元误差分量均方差与相关系数。 射击诸元误差分量的均方差及相关系数如表1。其中，同一设备引起的射击诸元误差分量的相关系数相等。

3)其他已知条件。φb0=1.187；σφb=0.38；R0=20 m；σG=3 m，v=550 m/s，θ=0.9εq。

对不同的r，3种算法算得的火炮武器系统毁伤概率如图3。

表1 射击诸元误差分量均方差与相关系数

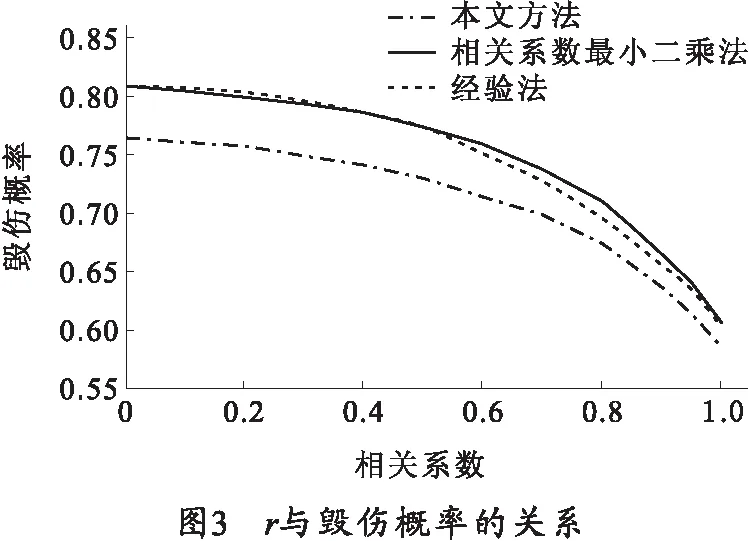
可以看出，在本例中，经验法优于相关系数最小二乘法。

3 结 论

基于射击诸元误差分量的相关性和重复性分析以及弱相关误差序列的随机生成，本文给出了近炸射击高炮系统点射毁伤概率的蒙特卡罗算法。在同样的前提条件下，以可承受的计算时耗为代价，蒙特卡罗法减小了误差模型转换法的近似性，给出了更为准确的计算结果。

从文中的给出的示例可以看出：1) 蒙特卡罗法和误差模型转换法的计算结果均表明，近炸射击高炮系统的点射毁伤概率将随着弱相关误差相关系数的增大而减小；2) 误差模型转换法所给出的毁伤概率计算结果稍大于蒙特卡罗法。

[1] 中国人民解放军炮兵装备技术研究所. GJBz 20499-98, 高炮武器系统射击效能评定[S]. 1998.

Artillery Technology Research Institute of PLA. GJBz 20499-98, Fire efficiency evaluation of antiaircraft gun system[S]. 1998. (in Chinese)

[2] 潘承泮，金忠. 高炮系统对导弹射击效力研究[J]. 弹箭与制导学报, 1995(4): 1-10.

PAN Chen-pan,JIN Zhong.Fire efficiency analysis of antiaircraft gun system to missile[J].Journal of Projectiles;Rockets;Missiles and Guidance,1995(4):1-10.(in Chinese)

[3] 王亮宽, 王蕊照, 薛庆阳. 某中口径火炮对巡航导弹毁歼概率研究[J]. 电子设计工程, 2010,18(6): 124-126.

WANG Liang-kuan, WANG Rui-zhao, XUE Qing-yang. Study on kill probability of medium caliber gun to cruiser guided missile[J]. Electronic Design Engineering, 2010,18(6): 124-126. (in Chinese)

[4] 李铁, 汪德虎, 潘红华. 近炸引信预制破片弹对空射击效率的研究[J]. 弹道学报, 2001,13(3): 1-7.

LI Tie, WANG De-hu, PAN Hong-hua. Firing efficiency study of proximity fuzed ammunition to aircraft[J]. Journal of Ballistics, 2001,13(3): 1-7. (in Chinese)

[5] 路航,石全,胡起伟,等.炮兵营射击的弹着点模拟及射击误差分析[J].指挥控制与仿真,2011,33(3):109-112.

LU Hang,SHI Quan,HU Qi-wei.et al.Analysis of firing error and simulation of impact position of artillery battalion[J].Command Control & Simulation,2011,33(3):109-112.(in Chinese)

[6] 宋承龄, 王章德. 系统仿真[M]. 北京: 国防工业出版社, 1985: 53-54.

SONG Cheng-ling, WANG Zhang-de. System simulation[M]. Beijing: National Defense Industry Press， 1985: 53-54. (in Chinese)

[7] 潘承泮. 武器系统射击效力分析[M]. 北京：国防工业出版社, 1994.

PAN Cheng-pan. Firing efficiency analysis of weapon system[M]. Beijing: National Defense Industry Press, 1994. (in Chinese)