电磁轨道炮热生成机理及温度场数值仿真

金龙文，雷 彬，张 倩，李 鹤，朱仁贵

(军械工程学院，河北 石家庄 050003)

1 电磁轨道炮热生成机理

电磁轨道炮的主体部分由两条平行的轨道和一个与轨道接触良好且能够沿着轨道自由滑动的电枢组成，如图1所示。接通电源后，电流沿着其中一条轨道流动，通过电枢，沿着另一条轨道流回。这时电枢在安培力的推动下沿着轨道加速运动，从而获得高速度。

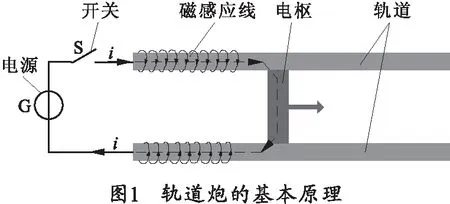
轨道炮的温升主要来自于电流生热和摩擦生热两个大方面，其中电流生热可以分为电枢和轨道本体的焦耳热温升和枢轨接触界面间接触电阻热温升两种表现形式。虽然这两种形式都是电流引起的温升，但是其计算方法有明显区别，因此可以分别考虑。轨道炮中的枢轨接触属于典型的载流摩擦磨损机制，电流导致的温升使接触界面材料软化，引起摩擦系数降低[1]；而摩擦副的相对运动对接触电阻的稳定性也会产生影响。

在轨道炮的发射过程中，由于轨道是摩擦副中的基体，随着电枢的滑动进入枢轨接触区域，并与电枢发生接触的轨道材料是未通过电流、温度较低的部分，因此，轨道具有一定的热分散作用；而电枢在发射过程中一直有大电流通过，而且始终与轨道发生摩擦作用，因此，电枢几乎不存在热分散功能。

此外，轨道炮对电枢的加速过程是在毫秒级内完成，热生成速率远大于传热速率。因此近似以绝热过程来处理，可以忽略与空气的热对流和对外界的热辐射。

2 仿真模型与计算参数的确定

根据实际轨道炮的结构特点，进行了部分简化后，针对电枢温度场的研究，建立了三维有限元模型。电枢的外围尺寸为20mm×20mm×36mm，单侧与轨道接触区域是20mm×26mm的方形。轨道材料取无氧高导性铜，电枢材料取2024-T3铝。

为了获得电枢本体的焦耳热温升，以电流作为激励对模型进行施加载荷。在实际实验中，采用脉冲成形网络(PFN)作为电磁轨道炮的电源；在数值仿真中，参考试验中测量到的电流波形，采用如图2所示的电流作为计算模型中的驱动电流。

2.1 接触电阻

电枢与轨道之间实际接触表面并不是光滑的平面，而是一个粗糙的、凹凸不平的表面，且覆有薄氧化膜和其他污染膜层。两种不同材料金属间接触电阻Rc是收缩电阻Rs和膜层电阻Rf之和，表示为[2]：

Rc=Rs+Rf=(ρ1+ρ2)/4a+σ/(πa2)

(1)

式中：ρ1、ρ2分别为两种接触金属的电阻率；a为金属间接触区域的半径；σ为膜层单位面积的电阻。

因为金属间接触斑点通常是在表面膜层被机械破坏后才能形成，因此，在绝大多情况下，膜层对总接触电阻的影响很小，在本次计算中忽略膜层电阻的存在。

在枢轨接触界面间，实际接触面积通常远小于名义接触面积，实际接触面积由下式决定[3-4]：

A1=P/nξH

(2)

式中：A1为单一接触点的面积；P为法向接触压力；n为接触点的数目；H为较软金属材料接触面的硬度；ξ为弹性变形的修正系数。在理论上，ξ为0～1之间的任意数都是可能的，但根据实际测量，接触力很大时ξ的值可以小到0.1以下[5]，在本次计算中取0.1。

为了保证轨道炮发射过程中电枢与轨道之间良好的电接触性能，需要在轨道和电枢之间加载预压力。预压力由Marshall的经验公式——“每安培1克”法则[6]得到，即：

Fpreload=0.01N/A

(3)

根据Kamran Daneshjoo等人[7]推导出的公式，可以计算出两轨道之间由电磁作用而引起的排斥力：

(4)

式中：m为自由空间磁导率(真空磁导率为μ0=4π×10-7H/m)；I为驱动电流；b是轨道宽度；r为两轨间距。由式(3)和式(4)，可以确定有效法向接触压力P。

通过计算得到，枢轨接触界面法向接触压力最大值为Pmax=4 000 N，而最小值为Pmin=2 172 N。为了简化计算，在仿真计算中设为常数P=3 000 N。准确地确定接触点的数目n是非常困难的，本次计算中根据前人的估算方法[2]：每4 mm2约10个，假设枢轨接触界面间具有1 300个接触点。最终，确定了枢轨接触的总接触电阻：

(5)

2.2 摩擦热流

电磁轨道炮的发射过程中，由于电枢和轨道间的高速滑动，将产生摩擦热。准确地评估摩擦时释放的热量是相当困难的。因此，通常可认为摩擦力做功转化为热量，其热流定义为：

qf=μPv

(6)

式中:μ为摩擦系数；P为接触压力，在本次计算中将用公式(2)中的P来代替；而v是枢轨间相对滑动速度。

未加润滑的接触在大电流情况下，接触表面的物理-力学性能将发生改变，例如会发生蠕变、咬合、氧化、转移及严重磨损等[2]。随着电流密度的增加，不同材料副间摩擦系数变化不同，通常情况下会上升，也有某些材料组合摩擦系数可能保持不变或下降。Brailford[8]针对铝、铜、黄铜及锡的未加润滑表面进行了载流摩擦研究，发现当电流通过时，接触点温度会上升到材料的软化温度甚至熔化温度以上。铝-铜之间摩擦系数随着电流的增加具有下降的趋势，但变化不明显。于是在本次计算中取摩擦系数为0.2。

此外，由于摩擦热流与电枢的速度呈线性关系，因此，需要对电枢进行运动学分析。电枢在运动方向上，主要受电磁力、摩擦力和空气阻力等3个方面的力。其中在t时刻作用于电枢上的电磁力表达式为：

(7)

式中：L′为电感梯度；I(t)为t时刻流入轨道炮的电流。电感梯度通过“克里斯克L′”[6]方法得到，其计算公式为：

L′={[A+Bln(F1)]ln(F2)}

(8)

式中：

F1=1+A1(w/h)+A2(w/h)(s/h)

(9)

F2=B1+B2(s/h)+B3(w/h)+B4(s/h)(w/h)

(10)

式中：h为轨道高度；w为轨道厚度；s为两个轨道内表面间的距离；Ai和Bi为常数。代入相关参数后，计算得到电感梯度为L′=0.35μH/m。

忽略空气阻力的影响时，t时刻电枢在运动方向上受到的合力为：

(11)

由此可以确定电枢的运动学方程为：

(12)

参照图3中的电流曲线，对上式进行分段积分后可以确定电枢的速度方程和位移方程。根据关键时间点上的速度值，确定了摩擦热流在此刻的大小，如表1所示。仿真参数中，摩擦热流载荷以斜坡形式在各时间点上进行施加，近似认为速度在时间区间内是线性增加的。

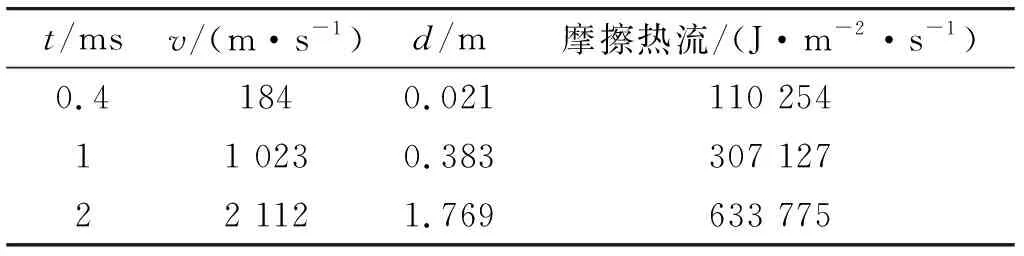
表1 仿真参数

3 仿真结果及分析

根据以上建立的三维有限元模型和相关的仿真参数，利用商业有限元软件Ansys进行了瞬态电热耦合数值仿真。仿真过程中，通过建立接触对(Contact Pair)模块的途径，设置了枢轨接触界面间的接触电阻；利用施加热流密度的方法，模拟了摩擦生热；仿真计算中电枢是静止不动的，未考虑到电流的速度屈服效应。图3为不同时刻电枢温度场的计算结果。

从以上温度分布云图中可以看出，电枢整体的温度随时间逐渐升高，其中U型拐角处温升相对其他区域比较明显，这与驱动电流流过电枢时的电流密度大小有关；而最高温度出现在与轨道接触部分表面的最前端靠两侧区域，其最高温度超过了铝的熔点。

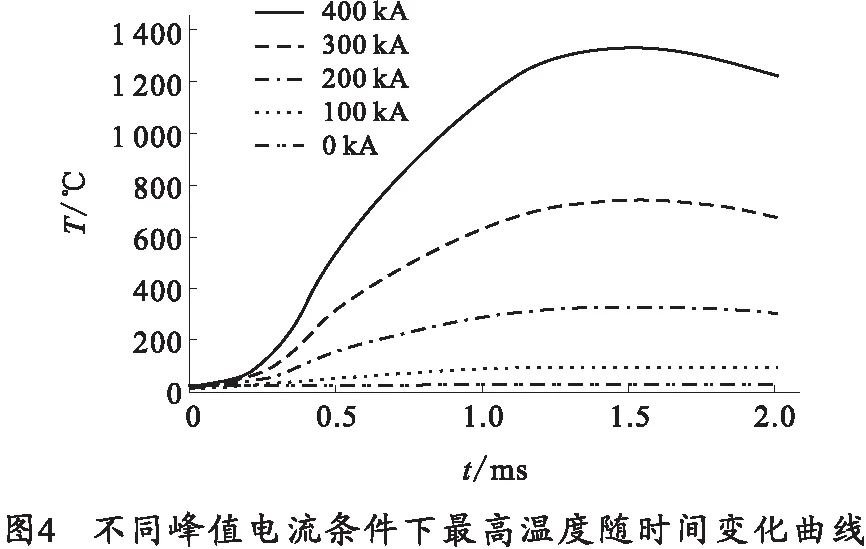
为了分析电流大小对电枢温度的影响，在不同的驱动电流条件下进行了有限元仿真。图4中5条曲线分别表示在400、300、200、100、0 kA峰值电流条件下和纯摩擦作用下，电枢的最高温度随时间变化曲线。结果显示，电枢在发射后不久温度上升较慢，随着电流的增加温度逐渐上升。在仿真中未考虑温度超过熔点的电枢材料在摩擦作用下磨损和脱落的现象，因此，随着时间的推移电枢的温度持续上升。从图中还可以看出，随着电流峰值的加大温度曲线发生显著的变化。在400 kA峰值电流条件下，电枢的最高温度超过了铝的熔点，但是峰值电流在300 kA以下时，并未发生电枢材料的熔化，而在纯摩擦作用下，温度的上升并不明显。这说明电枢的温度主要取决于电流的大小，而摩擦热对温升的影响较小。

在试验后的轨道表面观察中发现，轨道后端(炮尾处)以机械摩擦为主，磨损划痕较明显，说明电枢运动的初始阶段界面温度较低；随后逐渐形成白色磨损带而且平稳地延伸到轨道前端(炮口)。说明电枢表面材料在高温条件下发生熔化，在轨道表面上形成了熔层。 对轨道上的白色沉淀物进行了微观检测和EDS成分分析，如图5所示。

从微观形貌图中可以看出，沉积物是由多层含气孔的薄膜组成；成分分析结果表明，沉积物的主要成分为Al元素，还包括少量的Cu、Zn、O和C等元素。沉积物的结构和成分说明，电枢表面材料在高温下发生了熔化，在摩擦作用下磨损并脱落在轨道表面后，与铜材料和空气共同发生了反应；熔层迅速冷却后，在轨道表面形成了白色磨损带，而熔层中的部分空气来不及排除便形成了气孔。

此外，磨损带中沉淀物以电枢材料为主，这是因为电枢(Al)的熔点远低于轨道(Cu)的熔点；而且在发射过程中，电枢的热分散性能远不如于轨道的性能。

4 结 论

本文根据理论分析和数值仿真结果，并进行了相关试验验证后得出了以下结论：电枢的温升主要取决于电流的大小，而摩擦热对温升的影响较小；U型电枢中拐角部分的温升比较明显，这与电流密度大小有关；U型电枢中，最高温度出现在与轨道接触部分表面的最前端靠两侧区域，而且在本试验系统中峰值电流超过400 kA时，其温度超过了铝的熔点。

[1] CHEN Z,LIU P,VERHOEVEN J D,et al.Electrotribological behavior of Cu-15 vol.% Cr in situ composites under dry sliding[J].Wear,1997,203-204:28-35.

[2] BRAUNOVIC M, KONCHITS V, MYSHKIN K.电接触理论、应用与技术[M].北京：机械工业出版社，2010.

BRAUNOVIC M, KONCHITS V, MYSHKIN K. Electrical contacts fundamentals, applications and technology[M]. Beijing: China Machine Press, 2010. (in Chinese)

[3] BARBER J P. Contact current carrying limits [C].Proc 35th IEEE Holm Conference on Electrical Contacts, Chicago：Electrical Contacts,1989.

[4] HOLM R. Electric contact theory and application [M]. Berlin: Springer-Verlag, 1967.

[5] 程礼椿.电接触理论及应用[M].北京：机械工业出版社，1988.

CHENG Li-chun. Electrical contact theory and application [M]. Beijing: China Machine Press, 1988. (in Chinese)

[6] WANG Ying, MARSHALL R A. Railguns: their science and technology[M]. Beijing: China Machine Press, 2004.

[7] DANESHJOO K, AHMADI R, GHASSEMI M, et al. Dynamic response and armature critical velocity studies in an electromagnetic railgun[J]. IEEE Trans Magn, 2007,43(1):126-131.

[8] BRAILFORD J B. Influence of electrical current on static friction of metal surface in air[J]. Wear, 1973,25(1):85-97.