PMSG风力发电系统最大风能追踪的分数阶控制

李志民， 孙其振， 孙 勇， 韩绪鹏

(1.哈尔滨工业大学电气工程及自动化学院， 哈尔滨 150001；2.山东电力调度控制中心， 济南 250001；3.吉林省电力有限公司调度通信中心， 长春 130021；4.三峡电力职业学院电气工程系， 宜昌 443000)

PMSG风力发电系统最大风能追踪的分数阶控制

李志民1， 孙其振2， 孙 勇3， 韩绪鹏4

(1.哈尔滨工业大学电气工程及自动化学院， 哈尔滨 150001；2.山东电力调度控制中心， 济南 250001；3.吉林省电力有限公司调度通信中心， 长春 130021；4.三峡电力职业学院电气工程系， 宜昌 443000)

在总结分析基于永磁同步发电机PMSG(permanent magnet synchronous generator)的风力发电系统数学模型的基础上，以PMSG风力发电系统的最大风能追踪为控制目标，引入分数阶PIλ控制理论，设计了基于分数阶PIλ的PMSG风力发电系统控制方案，采用遗传算法对分数阶PIλ控制器的参数进行优化整定。在Matlab/Simulink软件平台上建立了PMSG风力发电系统的仿真模型，并与传统整数阶PI控制进行了对比。采用分数阶PIλ控制方案使风力机在额定风速以下能够有效地保持最佳叶尖速比运行，系统控制性能得到有效提高，有较强的鲁棒性。仿真结果证明了该方案的可行性与正确性。

分数阶控制； 最大风能追踪； 永磁同步发电机； 遗传算法； 建模与仿真

风能是一种洁净、低成本的可再生能源，针对风能的开发和利用已越来越受到世界各国的高度重视。由于风能的随机性与不稳定性，为了最大限度地追踪风能，在切入风速与额定风速之间风力机应保持最佳叶尖速比运行，此时对应的风能捕获效率最高[1]。文献[2]对风力发电系统的控制技术做了比较系统的研究，文献[3]研究了基于反馈线性化方法的永磁同步风力发电系统最大风能捕获控制。

为使工业控制过程得到更加满意的控制性能，分数阶微积分理论已在许多工程领域得到了应用，Podlubny教授将传统的比例积分PI(proportional integral)控制和比例积分微分PID(proportional integral differential)控制扩展为分数阶PIλ控制和分数阶PIλDμ控制[4]，分数阶控制器与传统整数阶控制器相比增加了可调实数参数，控制器参数的选取范围更大，可以更灵活地控制目标对象，具有更强的鲁棒性和更好的控制效果[5]。目前，分数阶控制理论在风力发电控制系统的应用是个比较新的领域，研究工作具有一定的理论和现实意义。国外有学者采用积分阶次为-0.5的分数阶PIλ控制器对风力发电机组中的电力电子变换器进行控制[6]，验证了采用分数阶PIλ控制比采用传统整数阶PI控制的控制性能更优，鲁棒性更好。分数阶PIλDμ控制器参数整定方法主要有：幅值裕量与相位裕量法，极点阶数搜索法，优化方法等，基于智能优化算法的控制器参数整定方法是分数阶PIλDμ控制器参数设计研究的一个重要分支[5，7]。

基于以上分析，本文提出了一种基于分数阶PIλ控制的PMSG风力发电系统最大风能追踪设计方案，并采用遗传算法对分数阶PIλ控制器的参数进行优化整定。利用Matlab/Simulink对基于分数阶PIλ控制的PMSG风力发电系统进行仿真，并与传统的整数阶PI控制进行对比分析，以研究分数阶控制在风力发电最大风能追踪控制中的应用，并研究分数阶控制方法的鲁棒性。

1 分数阶微积分理论

1.1 分数阶微积分的定义

分数阶微积分允许微分和积分的阶次为任意阶，最常用的分数微积分定义是Riemann-Liouviblle(RL)定义和Grünwald-Letnikov(GL)定义。RL与GL的定义分别为

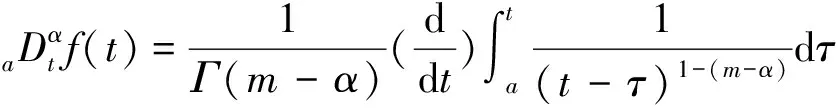
(1)

式中：m-1lt;αlt;m；Г(·)为Euler Gamma函数。

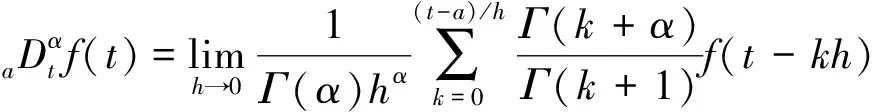
(2)

1.2 分数阶PIλ控制器

分数阶PIλ控制器时域表达式为

u(t)=Kpe(t)+KiD-λe(t)

(3)

由拉普拉斯变换，相应的传递函数为

(4)

由式(4)可知，传统整数阶PI是分数阶PIλ在λ取1时的一个特例。分数阶PIλ控制器框图如图1所示。

图1 分数阶PIλ控制器框图

分数阶PIλ控制器比传统的PI控制增加一个积分阶次λ，控制更加灵活，可以得到更为理想的控制效果，有效提高系统的性能[5，6]。

2 基于遗传算法的分数阶控制器参数整定

2.1 遗传算法步骤

遗传算法是模拟自然界遗传机制和生物进化论的一种并行随机搜索最优化方法，它通过遗传中的复制、交叉和变异对个体进行操作，逐步使群体中的个体适应度提高，最终得到全局最优解，算法简单。它已在自动控制、函数优化、组合优化等许多领域得到应用[7]。

应用遗传算法对分数阶PIλ控制器参数进行整定的步骤如下。

步骤1采用二进制编码方法对(Kp，Ki，λ)3个参数进行编码，生成初始群体。本文中编码串长度选择为10位。

步骤2确定参数的初始整定范围。根据实际经验大致确定初始参数范围，以缩小搜索空间并加快算法收敛。

步骤3计算适应度函数值。将算法中的参数(Kp，Ki，λ)三个参数代入到所编写的计算适应度函数值的程序中并返回。

步骤4对种群进行复制、交叉及变异操作。对适应度函数值高的个体进行复制，种群数量不变。交叉操作本文采用单点交叉，依据所设定的交叉概率Pc使选择的两个个体在交叉点处相互交换部分基因。最后根据设定的变异概率进行变异操作，使二进制编码中的1变为0，或0变为1。

步骤5通过复制、交叉及变异操作生成新一代种群，重新计算适应度函数值，检查是否满足结束条件，若不满足，重复以上操作，直至满足结束条件。

2.2 适应度函数

在遗传算法中适应度是评价个体优劣的依据，适应度高的个体遗传到下一代的概率较大，适应度函数的选取将直接影响遗传算法的性能，用于控制器设计的评价指标通常有绝对误差积分指标、平均误差积分指标以及时间加权平方误差积分指标等，本文所采用的优化目标函数H综合考虑了控制回路的误差e、上升时间tu以及超调量σ，其计算式为

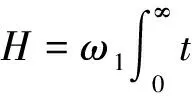
(5)

式中：ω1、ω2、ω3为权值；适应度函数f=1/H。

3 PMSG风力发电系统数学模型

变速恒频风力发机组是目前最常用的风能转换系统WECS(wind energy conversion system)之一，采用永磁同步发电机的变速恒频风力发电系统受到了研究者的重视[8]。PMSG风力发电系统主要由风轮机、传动链、永磁同步电机(PMSG)、电力电子变换器以及电网构成，其基本结构如图2所示。

图2 基于PMSG的风力发电系统

3.1 风力机及传动链数学模型

风力机的叶尖速比λ是衡量叶片转速与风速之比的变量，其数学定义为

(6)

式中：R为风轮半径；Ωl为风轮的角速度；v为风速。表示风能利用效率的功率系数Cp为桨距角β和叶尖速比λ的函数，当风机运行在切入风速和额定风速之间时，桨距角β=0，Cp为叶尖速比的函数，其计算式为

(7)

Cp与λ的关系曲线如图3所示。当叶尖速比为一个特定值λopt时有最大的风能利用系数Cpmax。最佳叶尖速比λopt=7对应Cpmax=0.476。

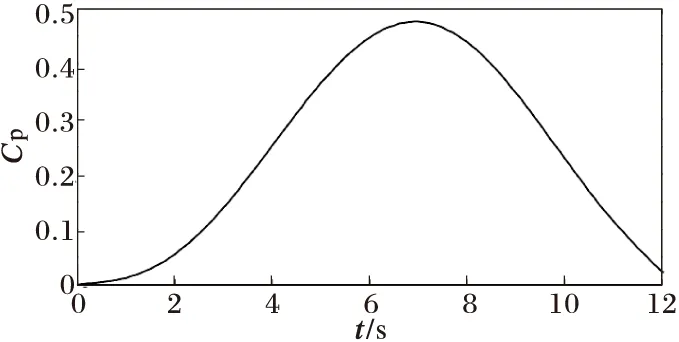
图3 Cp与λ的关系曲线

由空气动力学原理可知

Pwt=0.5ρπR2v3Cp(λ)

(8)

风力转矩方程可表示为

(9)

式中：CT为转矩系数；Pwt为风力机的捕获功率；ρ为空气密度。风力发电系统的传动链主要由低速轴LSS(low-speed shaft)，齿轮箱，高速轴HSS(high-speed shaft)组成，通过传动链，风力机将产生的机械能传递给永磁同步发电机转子，转子旋转进而产生电能。忽略静态和黏性摩擦，传动链的运动方程为

(10)

式中：Ωh为发电机转速，Ωh=iΩl；i为齿轮箱传动比；Tm为机械转矩，Tm=ηTM/i；η为齿轮箱效率；Te为发电机电磁转矩；J为高速轴的惯量。

3.2PMSG风力发电系统模型

假定PMSG为理想电机，通过Park变换实现三相(a，b，c)坐标系统到(d，q)两相坐标系统的转化，列写d-q坐标系下PMSG的数学模型为

(11)

电磁转矩为

TG=p[Ψmiq+(Ld-Lq)idiq]

(12)

根据式(6)～式(12)并对电力电子变换器和电网做简化处理[9]便可以得到PMSG风力发电系统方程。目前分数阶控制理论的应用主要针对线性系统，在复杂非线性系统上的应用难以解决。以PMSG的d轴电流id(t)，q轴电流iq(t)以及发电机转速Ωh为状态变量，设系统向由等效可变电阻R1和等效电感Ls并联的负荷供电，对系统方程在运行点附近线性化处理得线性化状态空间模型为

(13)

其中各参数表达式为

式中：ωs为发电机旋转电角速度；Rs为定子电阻；Ld为PMSG的d轴电感；Lq为PMSG的q轴电感；p为电机极对数；Ψm为由永磁体决定的恒值磁通；d1、d2、d3为与空气密度和风轮半径相关的常数；x10、x20、x30、R10为相应各变量在运行点处的稳态值。

4 分数阶微积分算子的近似整数阶处理

本文采用改进的Oustaloup滤波方法(Oustaloup recursive algorithm)对分数阶微积分算子进行近似整数阶处理，近似拟合的频率范围为[ωh，ωb]，阶次为N，一般取b=10，d=9。采用该方法所得的近似整数阶传递函数为

(14)

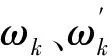
(15)

(16)

(17)

对积分算子只需取式(12)的倒数；对微积分算子sv，如果|v|gt;1，上述近似方法不够理想，因而对sv作sv=sn+δ处理，其中n∈Z，|δ|∈[0，1]，只需对sδ进行近似处理。

5 仿真结果及分析

根据PMSG风力发电系统的数学模型和分数阶PIλ控制理论，在Matlab/Simulink中搭建系统的仿真模型并进行仿真实验，其中已将分数阶控制器包括改进的Oustaloup滤波方法做成封装模块。在额定风速以下，控制发电机转速使其跟随风速变化以保持最佳叶尖速比，从而获得最大风能，实现风力发电系统的最大风能追踪，系统框图如图4所示。

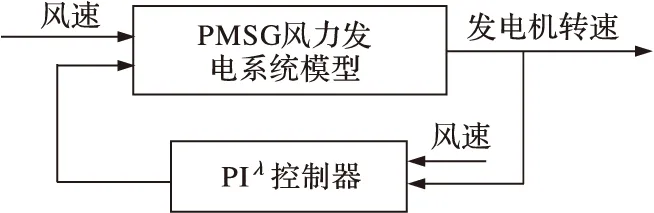
图4 PMSG风力发电系统控制框图

改进的Oustaloup滤波方法拟合频率选为[10-4，104]，近似阶次N=3。控制器设计采用遗传算法，其中种群数量S=14，进化代数G=100，交叉概率Pc=0.60，优化后得到分数阶控制器参数为(Kp，Ki，λ)=(1.0，7.5，-0.80)，按照同样优化算法设计的整数阶PID控制器参数为(Kp，Ki)=(1.0，4.0)。主要仿真参数主要仿真参数Rs=3.3 Ω，Ld=Lq=41.56 mH，Ψm=0.438 2 Wb，p=3，J=0.504 2 kg·m2。图5所示为风速曲线，风速模型利用冯卡门频谱模型模拟，平均风速为7 m/s；图6所示为分别采用分数阶PIλ控制和传统整数阶PI控制的PMSG转速曲线；图7所示为分别采用分数阶PIλ控制和传统整数阶PI控制的叶尖速比曲线；图8所示为分别采用分数阶PIλ控制和传统整数阶PI控制的风机功率系数Cp曲线。

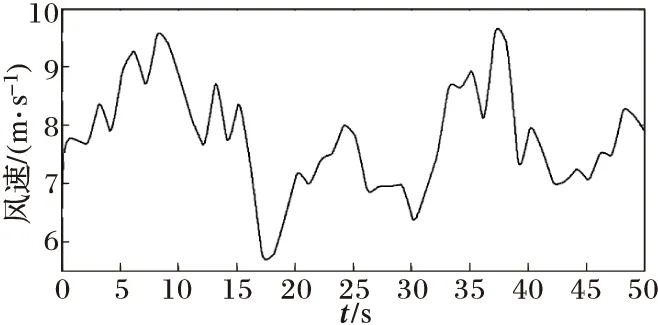
图5 风速曲线

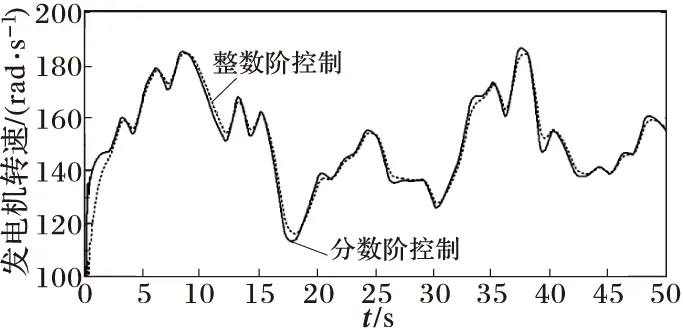
图6 发电机转速曲线

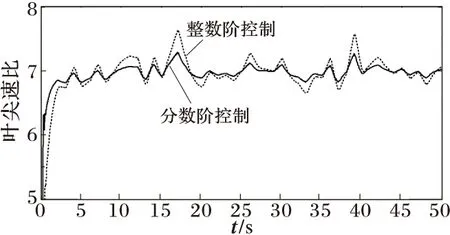
图7 叶尖速比曲线

图8 功率系数曲线

由图7可见，风力机在额定风速以下运行时，叶尖速比曲线在最佳叶尖速比λopt=7上下小范围内浮动，波动较小。由图8可见功率系数Cp保持在Cpmax=0.476，波动较小，从而证明了采用分数阶PIλ控制和传统整数阶PI控制两种控制策略均能达到控制目标，在风速随机变化的情况下实现PMSG风力发电系统的最大风能追踪。

对比分数阶PIλ控制和传统整数阶PI控制两种控制策略，从图7和图8的仿真结果可以得出，对基于PMSG的风力发电系统采用分数阶控制比采用传统整数阶控制响应速度更快，而且曲线更加平稳，控制效果更优。

为了进一步验证分数阶PIλ控制的鲁棒性，输入采用变化比较剧烈的阶跃风速，如图9所示。图10为分别采用分数阶PIλ控制和传统整数阶PI控制时的发电机转速曲线。由图10可见在风速变化波动较大的情况下，采用分数阶PIλ控制，发电机转速对风速有更快的追踪响应，鲁棒性较好。

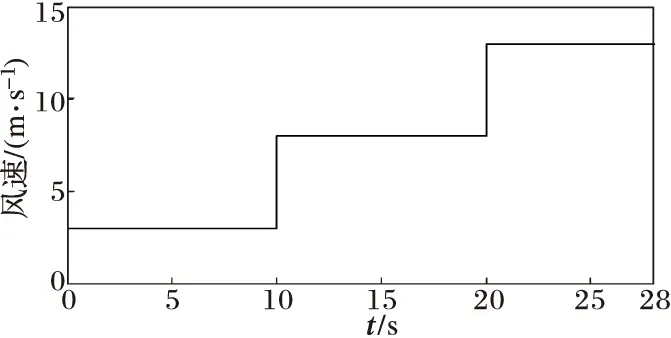
图9 阶跃风速

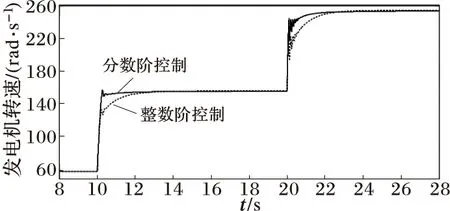
图10 分数阶控制下的发电机转速

6 结语

本文以PMSG风力发电系统的最大风能追踪为控制目标，提出了分数阶PIλ控制方案，对PMSG风力发电系统进行建模和仿真，实验证明所提出的分数阶PIλ控制方案不仅较好地实现控制目标，鲁棒性较好，而且系统控制性能更优，可以预见分数阶控制理论在风力发电领域中有良好的应用前景。

[1] 吴政球，干磊，曾议，等(Wu Zhengqiu, Gan Lei, Zeng Yi,etal).风力发电最大风能追踪综述(Summary of tracking the largest wind energy for wind power generation)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2009，21(4):88-93.

[2] 姚兴佳，温和煦，邓英(Yao Xingjia, Wen Hexu, Deng Ying).变速恒频风力发电系统变桨距智能控制(Adjustable pitch intelligent control of variable speed constant frequency wind generation system)[J].沈阳工业大学学报(Journal of Shenyang University of Technology)，2008，30(2):159-162，172.

[3] 王伟，陈奇，纪志成(Wang Wei, Chen Qi, Ji Zhicheng).基于反馈线性化的PMSG风力发电系统控制(Feedback linearization control of PMSG-based wind power generation system)[J].系统仿真学报(Journal of System Simulation)，2010，22(6): 1397-1401.

[4] Podlubny I. Fractional-order systems and PIλDμ-controllers [J].IEEE Trans on Automatic Control,1999,44(1):208-214.

[5] 薛定宇，赵春娜(Xue Dingyu, Zhao Chunna).分数阶系统的分数阶PID控制器设计(Fractional order PID controller design for fractional order system)[J].控制理论与应用(Control Theory amp; Applications)，2007，24(5):771-776.

[6] Meli′cio R, Mendes V M F, Catalao J P S. Power converter topologies and fractional-order controllers: Wind energy applications [C]∥International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Pisa Italy: 2010.

[7] 张力支,周激流,郎方年，等(Zhang Lizhi, Zhou Jiliu, Lang Fangnian,etal).用遗传算法优化设计分数阶微分器(Genetic algorithm for optimal design of fractional order differentiator)[J].四川大学学报：工程科学版(Journal of Sichaun University：Engineering Science Edition)，2008，40(1)：158-162.

[8] Yin Ming, Li Gengyin, Zhou Ming,etal. Modeling of the wind turbine with a permanent magnet synchronous generator for integration [C]∥IEEE Power Engineering Society General Meeting, Tampa, SA: 2007.〗

[9] Inlian M, Antoneta I B, Nicolaos A C,etal. Optimal Control of Wind Energy Systems [M]. London, UK: Springer, 2008.

[10]薛定宇，陈阳泉.高等应用数学问题的MATLAB求解[M].北京：清华大学出版社，2004.

李志民(1963-)，男，教授，博士生导师，研究方向为电力系统分析与控制。Email:lizhimin@hit.edu.cn

孙其振(1985-)，男，工程师，研究方向为分数阶控制理论与应用及分布式发电。Email:sqz09s@163.com

孙 勇(1980-)，男，博士，工程师，研究方向为风电调度与控制。Email:sunhao126@hotmail.com

MaximumEnergyTrackingofPMSGWindPowerGenerationSystembyFractional-orderControl

LI Zhi-min1， SUN Qi-zhen2， SUN Yong3， HAN Xu-peng4

(1.School of Electrical Engineering and Automation, Harbin Institute of Technology,Harbin 150001, China；2.Shandong Electric Power Dispatch and Control Center, Jinan 250001, China;3.Jilin Power Dispatch and Communication Center, Changchun 130021, China；4.Department of Electrical Engineering, Three Gorges Vocational College of Electric Power, Yichang 443000, China)

On the basis of analyzing the mathematical model of PMSG (permanent magnet synchronous generator) wind power generation system, to realize the control target of the maximum wind energy tracking for PMSG wind power system, a novel control theory of fractional order PIλcontrol is proposed and the PMSG wind power system control scheme is designed based on the fractional order PIλ. The genetic algorithm is applied to optimize and set the parameters of the design. A simulation model of PMSG wind power control system is established based on the Matlab/Simulink software platform. The novel fractional order PIλcontrol method is compared with the classical integer order PI control method. The proposed PIλcontrol method can effectively keep optimum tip-speed ratio under rated wind speed and the system control performance is improved with good robustness. The simulation results verify the validity and feasibility of the proposed control method.

fractional order control； maximum wind energy tracking； permanent magnet synchronous generator； genetic algorithm； model and simulation

TM614

A

1003-8930(2012)06-0067-06

2011-03-28；

2011-05-17