短期负荷预测的支持向量机参数选择方法

杨国健， 杨镜非， 童开蒙， 程浩忠， 孙毅斌， 叶 清

(1.上海交通大学电气工程系， 上海 200240； 2.上海电力公司青浦供电公司， 上海 201700)

短期负荷预测的支持向量机参数选择方法

杨国健1，2， 杨镜非1， 童开蒙1， 程浩忠1， 孙毅斌2， 叶 清2

(1.上海交通大学电气工程系， 上海 200240； 2.上海电力公司青浦供电公司， 上海 201700)

支持向量机SVM(support vector machine)方法的合理参数选择对提高回归结果的准确性有重要作用。该文采用基于支持向量机短期负荷预测的参数选择方法，用遗传算法对参数种群进行编码、交叉、复制和变异，求得最优参数和最优核函数。将该算法应用于电力系统短期负荷预测中，应用了筛选和不筛选特征值两种方案对历史数据进行了预测。算例证明，无论是应用筛选特征值方案还是不筛选特征值方案，参数选择对预测精度提高都具有重要作用。

支持向量机； 参数选择； 核函数选择； 负荷预测； 遗传算法

支持向量机[1]SVM(support vector machine)方法是一种基于统计分析和稳健回归理论的统计学习方法，它具有学习速度快、全局最优和推广能力强的优点，其学习结果经常明显好于其他的模式识别和回归预测方法，在电力系统短期负荷预测中，取得了较好的预测效果[2～4]。由于支持向量机在模型选取上需要对参数进行选择，而目前应用于短期负荷预测的支持向量机法多半是通过个人设计经验来进行参数选择，具有非常强的主观性和随意性，因而有必要采用自适应优化算法对参数进行客观选择，来提高支持向量机训练的精度。

本文提出了支持向量机短期负荷预测的参数选择方法，采用变参数的SVM作为负荷预测的模型，通过遗传算法对参数进行编码、交叉、复制和变异，以求得最优参数。这种方法利用了SVM良好的回归能力，同时又能够通过参数种群的进化寻觅到最优的参数。在特征值选取问题上，提出了基于数据特征值筛选的方法和未经筛选的方法，分析比较了两种方法的误差结果。

1 支持向量机模型

支持向量机是一种统计学习方法，它对l个数据进行训练，其中第i个数据包含自变量xi∈Rn和与之相对应的因变量yi∈R。SVM定义映射函数

f(x)=k(x，x′)+b

(1)

此函数反映自变量x和因变量f(x)的关系，其中x，x′∈Rn，f(x)∈R，k(x，x′)=⟨φ(x)，φ(x′)⟩称为核函数，φ：X→τ是一种τ的映射。SVM的数学模型为

subject toyi-⟨φ(x′)，xi⟩-

b≤ε+εi⟨φ(x′)，xi⟩+

(2)

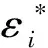
线性函数

k(x，x′)=⟨x，x′⟩

(3)

多项式函数

k(x，x′)=(γ⟨x，x′⟩+δ)d

(4)

径向基函数

k(x，x′)=e-γ‖x-x′‖2

(5)

对数S型函数

k(x，x′)=tanh(γ*⟨x，x′⟩+δ)

(6)

经证明[2]，上述函数符合φ(x)能将x映射到τ特征空间的条件，可以作为支持向量机中的核函数。

回归问题的实质是一个优化问题，它的求解有多种算法，如IBM公司在1992年推出的OSL算法，1995年Cortes和Vapnik提出的Chunking算法、内点法、序列极小化[5]， Chih-Jen Lin于2005年提出的LIBSVM方法[6]等。

2 基于遗传算法的支持向量机参数选择

选取好的SVM参数，提高模型的模式识别能力非常重要[1，6]，本文提出一种基于遗传算法的SVM参数选择方法。SVM中需要进行用户选择的参数有：1)核函数类型；2)惩罚因子C；3)期望最大绝对误差ε；4)核函数的内部参数γ，δ，d。由于不同核函数的参数没有可比性，故本文提出先对同一种核函数内部用遗传算法进行参数选择，再把每种核函数的最优参数的结果进行比较，用于选择最佳的拟合方案。下面以径向基函数为例，说明基于遗传算法的SVM参数选择方法。

径向基函数的表达式为k(x，x′)=e-γ‖x-x′‖2，因而需要选择的参数有3个：γ，C，ε，采用通用的二进制编码，将这些变量都转化为相应的0、1编码。建立一个包含所有参数的二进制编码的种群，通过随机填入数字0或1对这些种群变量进行初始化赋值，对每一个种群，将二进制变量还原为十进制变量，找到使式(1)达到最优解的x′和b，然后相应地最佳拟合函数f(x)=k(x，x′)+b的训练误差E为

(7)

定义适应度函数

F=E+ct

(8)

式中：t为训练时间；c为训练时间系数。这样的适应度函数既考虑到训练的精度，又考虑到训练的速度，目的是防止大规模数据在寻优过程中速度过慢。找出适应度函数较小的染色体，不断进行交叉和复制、变异，直到满足以下两个遗传中止条件之一：1)适应度函数小于给定的适应度函数限值；2)两代最优适应度函数的差值小于给定的差值限值。此时，该染色体所对应的参数被认为是问题的最优参数。图1示出了支持向量机参数选择的流程图。

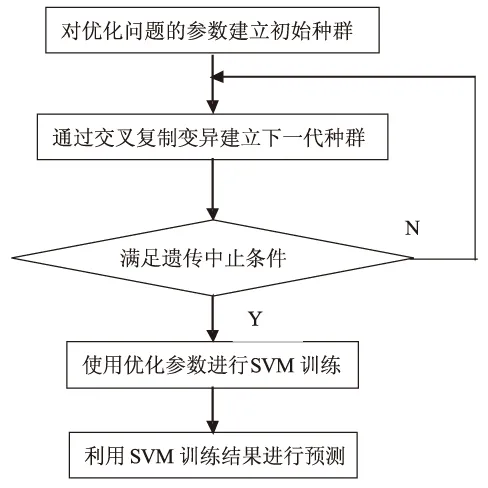
图1 固定核函数的支持向量机参数选择流程

前面描述的是对同一种核函数内部用遗传算法进行参数选择并进行负荷预测的方法，考虑到不同核函数在不同训练背景下的预测精度不同，本文提出在对同一核函数进行参数选择的基础上，再把每种核函数的最优参数的结果进行比较，用于筛选最佳核函数，选择最佳的拟合方案。步骤如下：

1)利用遗传算法对各种不同核函数选择最佳参数值；

2)计算对每种核函数最佳参数值对应训练误差E；

3)将训练误差E最小值所对应的核函数作为筛选核函数；

4)利用筛选核函数以及相应的最佳参数值进行SVM预测。

这里采用了训练误差E而没有采用适应度函数F作为优化目标，原因是在前述的不同核函数参数优选的过程中，已经考虑过训练时间，核函数筛选后不需要再对各种核函数进行再次训练，只需要根据最优参数直接得出被预测量的映射函数解析解，因此不会影响预测时间的长短。这种情况下，精度最优是筛选最优核函数唯一需要考虑的因素。

3 支持向量机负荷预测方法的参数选择

本文采用的算例是对2010年河南电网连续30天的负荷情况进行日负荷预测。给出的已知数据是河南电网每天48个采样点的负荷数据、每天平均气温数据以及被预测日的气象预报数据，历史数据的时间长度是从2008年1月1日到被预测日之前36小时的时间段，预测的对象是每个预测日全天48点的负荷数据。对于特征值的选取，使用两套方案来预测训练样本。第一套方案，首先筛选出和预测点在星期属性、节假日属性、预测时段都相同且和预测日的时间距离小于两年的数据作为SVM中的y值，相应的x值共有9个特征输入量，包括训练点前一天与预测时段相同的负荷、提前一个时段的负荷、提前两个时段的负荷、训练点的温度、训练点前1～5天的与预测时段相同时段的负荷。第二套方案，不进行筛选，找出所有和预测点的时间距离小于两年的数据作为SVM中的y值，相应的x值除了第一套方案中的9个特征输入量外，还包含星期属性、节假日属性和预测时段。本例中设置训练时间系数c=10-4，训练时间单位为 s。算例做了30次日负荷预测，每次预测某日48个点的负荷，一共预测了1440(30×48)个预测点，表1列出了这1440个点的平均绝对百分误差MAPE(mean absolute percentage error)和绝对百分误差最大值APEM(absolute percentage error maximum)。

表1 连续30天日负荷预测结果的误差情况

表1中可以看出，无参数优化的预测误差明显高于考虑参数优化的误差，证实了参数优化的重要作用。在考虑参数优化训练结果中，采用第一套方案对这些日负荷对应的1440个点进行预测，最佳核函数为多项式函数的有963个点，为线性函数的有358个点，为径向基函数的有119个点。而采用第二套方案，1440个点的最佳核函数均为径向基函数。对这个结果进行更进一步的分析，发现第一套方案中963个最佳核函数为多项式的点，其多项式指数d大多接近于1，也就是说其多项式表达式大多数都接近线性。这是由于在第一套方案中，数据筛选模块已经将分散性比较强的数据分割为几大类，每类内部的数据具有相似的变化规律，基本可以用线性来表示。而在第二套方案中，数据点较为分散，由文献[7]可以证明，径向基函数对于这类问题的描述更为准确。另外从表1中还可以看出，经过筛选最佳函数后的预测结果明显优于未经筛选的数据，证明了筛选函数的重要性。 图2为某日实际负荷和预测负荷对比曲线图，预测方法采用第一套方案并进行了核函数筛选，从图中可以看出，本文所提的预测方法具有较高的预测精度。

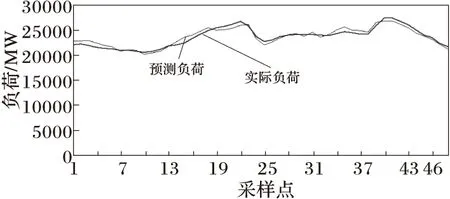
图2 某日实际负荷曲线与预测负荷曲线对比

4 结语

本文提出了支持向量机负荷预测的参数选择方法，首先用SVM写出预测的数学模型并进行求解，再通过遗传算法对参数进行编码、交叉、复制和变异，以求得最优参数。最后以训练误差最小作为目标函数，筛选出最优核函数。将该算法应用于电力系统短期负荷预测中，考虑到影响负荷的要素，对历史数据进行筛选，找出与预测点属同一类的数据进行训练。

河南电网的算例证明了考虑参数优化对提高预测精度的作用。在算例结果中，采用筛选后的数据的最佳核函数多为接近线性表达式，且经过筛选的数据进行预测的结果优于未经筛选的数据，说明了特征值的选择对于支持向量机的重要作用。误差结果显示，支持向量机负荷预测的参数选择法结果合理、精度高、具有应用价值。

[1] Vapnik V.The Nature of Statistical Learning Theory [M].New York:Spdnge-Verlag, 1995.

[2] 赵登福，王蒙， 张讲社，等(Zhao Dengfu, Wang Men-g, Zhang Jiangshe,etal). 基于支撑向量机方法的短期负荷预测(A support vector machine approach for short term load forecasting)[J]. 中国电机工程学报(Proceedings of the CSEE), 2002, 22(4):26-30.

[3] Keerthi S S, Shevade S K, Bhattacharyya C,etal.Improvements to Platt's SMO algorithm for SVM classifier design [J]. Neural Computation, 2001,13(3): 637-649.

[4] Chang C, Lin C. LIBSVM: a library for support vector machines[EB/OL]. http://www.csie.ntu.edu.tw/～cjlin/libsvm, 2002.

[5] 吴宗敏(Wu Zongmin). 径向基函数、散乱数据拟合与无网格偏微分方程数值解(Radial basis function scattered data interpolation and the meshless method of numerical solution of PDEs)[J]. 工程数学学报(Journal of Engineering Mathematics), 2002, 19(2): 1-12.

[6] 蒋喆(Jiang Zhe). 支持向量机在电力负荷预测中的应用研究(Research on power load forecasting base on support vector machines)[J]. 计算机仿真(Computer Simulation), 2010, 27(8): 282-285.

[7] 叶淳铮, 常鲜戎, 顾为国(Ye Chunzheng, Chang Xianrong, Gu Weiguo). 基于小波变换和支持向量机的电力系统短期负荷预测(Short-term load forecasting based on wavelet transform and support vector machines)[J]. 电力系统保护与控制(Power System Protection and Control) , 2009,37(14):41-45.

[8] 梁建武，陈祖权，谭海龙(Liang Jianwu, Chen Zuquan, Tan Hailong). 短期负荷预测的聚类组合和支持向量机方法(Application of clustering combination and support vector machine in short-term load forecasting)[J]. 电力系统及其自动化学报(Proceedings of the CSU-EPSA) , 2011,23(1):34-38.

杨国健(1978-)，男，硕士研究生，工程师，研究方向为负荷预测、配电网运行优化。Email:cn_yangcn@sina.com

杨镜非(1974-)，女，副教授，研究方向为负荷预测、智能电网、变电站仿真。Email:carayang@sjtu.edu.cn

童开蒙(1987-)，男，硕士研究生，研究方向为负荷预测、配电网运行优化。Email:kaikai.sjtu@hotmail.com

ParameterSelectionofSupportVectorMachineforShort-termLoadForecasting

YANG Guo-jian1，2， YANG Jing-fei1， TONG Kai-meng1，CHENG Hao-zhong1， SUN Yi-bin2， YE Qing2

(1.Department of Electrical Engineering, Shanghai Jiaotong University,Shanghai 200240, China;2.Qingpu Power Supply Branch, Shanghai Municipal Electric Power Company,Shanghai 201700, China)

The parameter selection of support vector machine (SVM) play a key role in increasing the accuracy of short-term load forecasting result. The method of SVM parameter selection for short-term load forecasting is presented in this paper which the parameters in a binary group are coded, crossed, reproduced and mutated on the base of genetic algorithm to find the optimal parameter and kernel function. The choosing and non-choosing eigenvalue scheme is used for short-term load forecasting and the results show that parameter selection is important for improving the forecasting accuracy no matter which eigenvalue scheme.

support vector machine(SVM)； parameter selection； kernel selection； load forecasting; genetic algorithm

TM61

A

1003-8930(2012)06-0148-04

2011-08-17；

2011-10-08