数学形态学和ESPRIT在低频振荡分析中的应用

聂永辉， 荣令玉， 张立艳

(1.东北电力大学教务处， 吉林 132012； 2.西安交通大学电气工程学院， 西安 710049；3.华能九台电厂运行部， 吉林 130501； 4.陕西省电力公司铜川供电局， 铜川 727100)

数学形态学和ESPRIT在低频振荡分析中的应用

聂永辉1，2， 荣令玉3， 张立艳4

(1.东北电力大学教务处， 吉林 132012； 2.西安交通大学电气工程学院， 西安 710049；3.华能九台电厂运行部， 吉林 130501； 4.陕西省电力公司铜川供电局， 铜川 727100)

为了准确地辨识电力系统低频振荡模态参数，该文提出了基于数学形态学MM(mathematical morphology)和总体最小二乘法的旋转不变技术TLS-ESPRIT (total least squares-estimation of signal parameters via rotational invariance technique)的电力系统低频振荡模态参数识别新方法。首先运用基于数学形态学原理而构成形态滤波器对含有噪声的电力系统低频振荡测量信号进行滤波和平稳化处理，去除噪声，提高辨识精度；然后由TLS-ESPRIT算法辨识出电力系统低频振荡模态参数，该算法把信号分成信号子空间和噪声子空间，能够得到更符合电力系统实际的降阶模型和主导模态，有助于电力系统振荡特性分析和阻尼控制器的设计研究。数值仿真分析表明该方法的可行性和有效性。

低频振荡； 参数辨识； 总体最小二乘法-旋转不变技术； 数学形态学； 主导模态

目前，电力系统的规模不断扩大，长距离输电和弱联网现象增多，弱阻尼的低频振荡正成为限制互联电网传输能力的瓶颈，严重威胁电力系统的安全稳定运行，正确监测和分析系统低频振荡特性，成为实现有效的阻尼控制并进而提高大型电网稳定性的关键技术。

多年来，各种方法用来研究低频振荡问题，其中包括特征值分析法、Prony方法等。特征值分析法[1]是研究电力系统低频振荡的一种经典方法，但随系统规模及复杂程度的不断增加，传统方法日益暴露出其不足。

Prony及其改进方法[2～8]是一种模态参数辨识的时域方法，近年来被广泛应用于分析电力系统低频振荡和控制器参数优化等场合。Prony方法是一种基于多项式的算法，先通过各种方法求得观测数据满足的多项式,然后再通过求解多项式的根来辨识低频振荡的频率、阻尼等信息。所以Prony方法对噪声比较敏感。

本文提出了基于数学形态学和总体最小二乘法的旋转不变技术的电力系统低频振荡模态参数识别新方法。首先运用基于数学形态学原理而构成形态滤波器对含有噪声的电力系统低频振荡测量信号进行滤波和平稳化处理，去除噪声，提高辨识精度；然后由TLS-ESPRIT算法辨识出电力系统低频振荡模态参数，该算法把信号分成信号子空间和噪声子空间，能够得到更符合电力系统实际的降阶模型和主导模态，有助于电力系统振荡特性分析和阻尼控制器的设计研究。

1 理论介绍

1.1 数学形态学理论介绍

数学形态学[8，9]是一种非线性信号处理和分析方法。其基本思想是通过一个称作结构元素的“探针”(相当于滤波窗)在信号中不断移动，将复杂信号分解为具有物理意义的各部分，以考察信号各部分之间的相互关联，并提取有用信息来描述信号特征。

数学形态学的基本运算包括膨胀、腐蚀以及形态开、闭运算。由于电力系统的信号一般为一维信号，这里只介绍一维离散情况下的形态变换。

设输入序列f(n)，g(n)分别是F={0，1，…，N-1}和G={0，1，…，M-1}上的离散函数，且Ngt;M。用g(n)对信号f(n)进行膨胀和腐蚀分别定义如下：

(f⊕g)(n)=max{f(n-m)+g(m)|(n-

m)∈F，n∈G}

(1)

(fΘg)(n)=min{f(n+m)-g(m)|(n-

m)∈F，n∈G}

(2)

集合g在形态学中称为结构元素，结构元素的设计一般取决于滤波后要保持的信号形状。

膨胀和腐蚀具有以下性质：

(fc⊕gc)(n)=(fΘg)(n)

(3)

(fcΘgc)(n)=(f⊕g)(n)

(4)

c表示取补集，上述性质称为膨胀和腐蚀的对偶性，除此之外，膨胀和腐蚀还具有结合性、平移不变性、交换率和递增性。

在膨胀和腐蚀基础上，定义形态开运算、形态闭运算、开-闭运算、闭-开运算分别如下：

(f∘g)(n)=(fΘg⊕g)(n)

(5)

(f·g)(n)=(f⊕gΘg)(n)

(6)

foc(n)=(f∘g·g)(n)

(7)

fco(n)=(f·g∘g)(n)

(8)

在信号处理中，开运算可去掉信号峰值(正脉冲)噪声，去除信号边缘毛刺、孤立斑点及小桥结构，即对信号进行平滑；闭运算可抑制信号低谷(负脉冲)噪声，填补孔洞和裂缝。可见，形态开、闭运算均具有滤波功能。

1.2TLS-ESPRIT算法介绍

ESPRIT方法是1986年由ROY等人[10～12]提出的，假设信号由一系列幅值按指数规律变化的正弦信号与白噪声组合，而电力系统低频振荡信号正好符合这一特点，在采样时刻，其表达式为

(9)

式中：sk=akejθk，ak和θk分别为第k个模态的幅值和初始相位；ωk、σk分别为第k个模态的频率和衰减因子；w(n)为高斯白噪声。当信号为实信号时，p为信号实际含有的实正弦分量个数的两倍。

对于连续M时刻观测值可以写成向量形式：

X(n)=[x(n)，…，x(n+M-1)]T=

As(n)+w(n)

(10)

其中：A为M×p信号频率矩阵；s(n)为复幅值信号向量，表达式为：

(11)

设Φ=diag(e-σ1+jω1，…，e-σp+jωp)，则：

Y(n)=X(n+1)=AΦs(n)+w(n+1)

(12)

A2=A1Φ

(13)

式中：矩阵A1和A2为矩阵A删除第一行和最后一行所得，因此Φ为旋转矩阵，这就是旋转不变性的解释。根据旋转矩阵可求出信号的频率，从而进一步可求出某一频率信号的所有参数。

为了实现从被噪声污染的实测数据或者时域仿真数据中估计出信号的参数，本文采用根据HANKEL矩阵实现TLS-ESPRIT算法。具体实现步骤简述如下。

根据观测数据序列x(0)，x(1)，…，x(N-1)构造Hankel数据矩阵

XL×M=[x(0)，x(1)，…，x(M-1)]=

(14)

式中：Lgt;P，Mgt;P，L+M-1=N，L通常取N/4～N/3。

对X进行奇异值分解得

X=U∑VH

(15)

式中：∑为对角阵，对角元素按ξ1≥ξ2≥…≥ξpgt;ξp+1≈…≈ξmin(L,M)≈0的降序排列，此时，可将V按奇异值大小划分为信号子空间V1和噪声子空间V2。ξ1，ξ2，……，ξp所对应的右奇异向量为信号子空间V1的各列向量。

利用总体最小二乘求解，令V↑和V↓分别表示信号子空间矩阵V1删除第一行和最后一行的矩阵，根据式(13)有如下方程成立：

(V↑+e1)=(V↓+e2)φ

(16)

式中：矩阵φ和式(13)中的旋转矩阵Φ是相似矩阵，具有相同的特征值，e1，e2为扰动矩阵(可认为信号中存在的噪声和其他一些干扰)，求方程(16)的最优解φ，使扰动矩阵D=[-e1，e2]的Fronenius范数取得最优值，这是总体最小二乘求解思想。

计算φ的特征值λk(k=1，2，…，p)，便可计算出原信号中各分量频率和衰减因子，计算公式为

(17)

(18)

对于N个采样信号组成的向量X，有X=λs，其中：

(19)

根据最小二乘法得出s=(λTλ)-1λTX，从而可估计出信号中各分量的幅值和相位：

ak=2|sk|，θk=arg(sk)k=1，2，…，p

(20)

2 实现问题

2.1 形态滤波器实现问题

电力系统的测量数据均为非线性非平稳含有噪声的信号，经形态滤波器滤去原始信号中的噪声，从而提高检测低频振荡分量的精度。

目前运用较多的形态滤波器是由前面介绍的开-闭运算foc(n)和闭-开运算fco(n)组合而成：

(21)

该滤波器的优点是可同时抑制信号中的正、负脉冲噪声，但由于在级联过程中使用了相同的结构元素，导致其只能对一种噪声有较好的滤波效果，而不能很好地处理各种噪声。形态滤波器的滤波效果既取决于变换的方式，又与结构元素的尺寸和形状有关。一般只有与结构元素相匹配的信号才能被保持。本文构造由半圆结构元素和三角形结构元素两种结构元素组成的实时形态滤波器，从而滤除白噪声和脉冲噪声等多种干扰。

设f(n)为定义在F={0，1，…，N-1}上的离散信号，两个结构元素分别为g1(n)(n∈G1)和g2(n)(n∈G2)。则形态开-闭和闭-开滤波器分别定义为：

foc(n)=(f∘g1·g2)(n)

(22)

fco(n)=(f·g1∘g2)(n)

(23)

按照式(21)，利用形态开-闭和闭-开运算的平均组合而成形态滤波器，既能消除形态算子产生的统计偏移，又能更好地保持原信号几何特征。

2.2TLS-ESPRIT算法实现问题

采用TLS-ESPRIT算法，信号模型阶数在计算过程中更易确定。通常当igt;p时，由式(15)得到的矩阵X的奇异值ξi会减小。若存在整数使得：

(24)

则可近似地p=[i/2]×2取为降维模型阶数，[·]表示向上取整函数。参数k取决于测量信号的噪声水平等，可通过观察ξi变化或根据经验确定。

3 仿真结果

3.1 测试信号分析

电力系统低频振荡信号由一系列幅值按指数规律变化的正弦信号与白噪声组合，还可表示为：

(25)

构造一个含有噪声的低频振荡测试信号，具体参数如表1，w(t)为白噪声，幅值为0.2。该信号频率集中在0.1～2.5 Hz之间，可较好地模拟低频振荡信号的主要特点。对现场数据来说，过高的采样率会带入不必要的高频噪声信号，所以低频振荡测试信号的采样频率不必过高，本文取40 Hz。

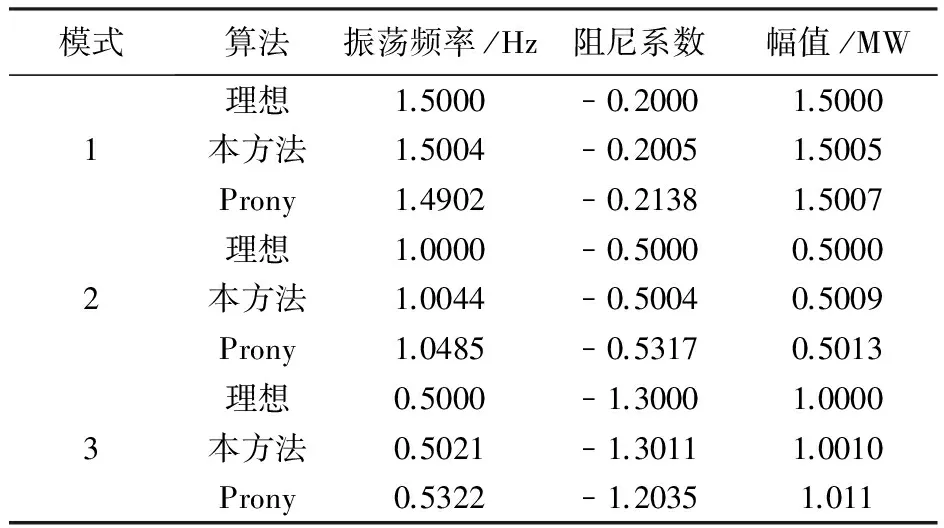
表1 理想低频振荡模态分量参数与辨识结果

图1为加入噪声干扰后的低频振荡测试信号，图2为理想低频振荡测试信号，图3为去噪后的低频振荡测试信号，可以看出形态滤波器有效地去除了噪声，保留了低频振荡信号的特征。

图1 含噪的低频振荡测试信号

为说明本文方法的有效性，将本文方法与基于原始Prony方法的辨识结果进行比较，最终辨识出的参数如表1 。仿真结果可知，在较大噪声环境下，采用Prony方法辨识得到的振荡频率和阻尼系数的最大相对误差为6.4%和7.4%；而采用本方法辨识得到的振荡频率和阻尼系数的最大相对误差为0.44%和0.08%。可见，本文方法能够对低频振荡信号进行有效的模态分离和参数辨识。

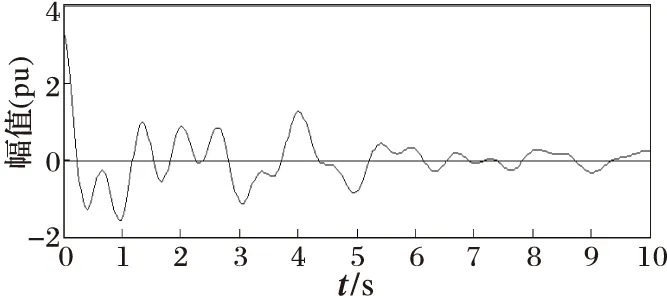
图2 理想低频振荡测试信号

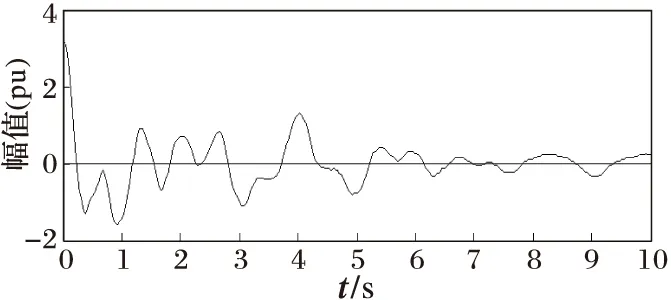
图3 去噪的低频振荡测试信号

3.2 四机两区域系统分析

为验证本文算法的有效性，在MATLAB平台上搭建四机两区域仿真系统进行低频振荡分析，系统接线图如图4所示，具体参数见文献[13]。采用白噪声激励G1发电机的励磁模块参考电压，作用时间为20 s。采集G4发电机的相对功角摇摆曲线，如图5所示。

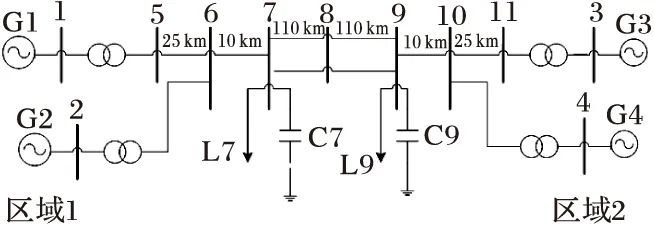
图4 四机两区域系统接线图

图5 G4相对功角振荡曲线

利用该方法对功角振荡数据进行辨识，可以得出降阶模型的模式参数，分析得出系统的主振荡频率为0.6 Hz，这和图6显示的FFT变换的结果是一致的，具体辨识结果见表2。

图6 G4相对功角曲线的FFT变换频谱图

表2 辨识结果

4 结语

本文将基于数学形态学和总体最小二乘法的旋转不变技术应用于电力系统低频振荡模态参数识别。数学形态滤波器能有效去除低频振荡测量信号所含噪声，对其进行滤波和平稳化处理，提高辨识精度；由TLS-ESPRIT算法辨识出电力系统的降阶模型，得到系统的主振模态，能反映系统实际状态，为电力系统稳定器的安装提供参考依据。

[1] 李天云，谢家安，张方彦，等(Li Tianyun，Xie Jia'an，Zhang Fangyan，etal).HHT在电力系统低频振荡模态参数提取中的应用(Application of HHT for extracting the model parameters of low frequency oscillations in power systems) [J]．中国电机工程学报(Proceedings of the CSEE)，2007，27(28) ：79-83．

[2] 刘红超，李兴源(Liu Hongchao，Li Xingyuan)．基于PRONY辨识的交直流并联输电系统直流阻尼控制的研究(Study of DC damping control in AC/DC transmission systems based on Prony method)[J]．中国电机工程学报(Proceedings of the CSEE)，2002，22(7)：54-57．

[3] 袁荣湘，江保锋，赵树华，等(Yuan Rongxiang，Jiang Baofeng，Zhao Shuhua，etal)．随机子空间法在低频振荡分析中的应用(Stochastic subspace identification for power system low frequency oscillations analysis) [J]．电 力 系 统 及 其 自 动 化 学 报(Proceedings of the CSU-EPSA)，2011，23(4)：51-55．

[4] 肖晋宇，谢晓荣，胡志祥，等(Xiao Jinyu，Xie Xiaorong，Hu Zhixiang，etal)．电力系统低频振荡在线辨识的改进Prony算法(Improved Prony method for online identification of low frequency oscillation in power systems) [J]. 清华大学学报(自然科学版)(Journal of Tsinghua University(Science and Technology))， 2004，44(7)：883-887.

[5] 徐东杰，贺仁睦，胡国强，等(Xu Dongjie，He Renmu，Hu Guoqiang，etal)．正规形方法在互联电网低频振荡分析中的应用(Analysis of low frequency oscillations using normal form method) [J]．中国电机工程学报(Proceedings of the CSEE)，2004，24(3)：18-23．

[6] 韩祯祥，吴复霞，吴浩，等(Han Zhenxiang，Wu Fuxia，Wu Hao，etal)．电力系统低频振荡的差频现象研究(Investigation of the low frequency oscillation in complex power system)[J]．中国电机工程学报(Proceedings of the CSEE)，2005，25(25)：1-5．

[7] 李天云，高磊，赵妍(Li Tianyun，Gao Lei, Zhao Yan).基于HHT的电力系统低频振荡分析(Analysis of low frequency oscillations using HHT method) [J].中国电机工程学报(Proceedings of the CSEE)，2006，26(14)：24-30．

[8] 唐常青，吕宏伯，黄铮，等．数学形态学方法及其应用[M]． 北京：科学出版社，1990．

[9] 邹力，赵青春，林湘宁，等(Zou Li，Zhao Qingchun，Lin Xiangning，etal)．基于数学形态学的电力系统振荡中故障识别和改进的选相方法(Mathematical morphology based fault detector and improved phase selector in power swing) [J]. 中国电机工程学报(Proceedings of the CSEE)，2006，26(13)：37-42．

[10]Roy R， Kailath T．ESPRIT-estimation of signal parameters via rotational invariance techniques [J]．IEEE Trans on Acoustics，Speech and Signal Processing，1989，37(7): 984-995．

[11]张贤达．矩阵分析与应用[M]．北京：清华大学出版社，2004．

[12]聂永辉，刘彦臣，张立艳(Nie Yonghui，Liu Yanchen，Zhang Liyan)．TLS-ESPRIT 技术在电力系统谐波检测的应用(Application of TLS-ESPRIT on harmonic measurement of power system)[J]． 电 力 系 统 及 其 自 动 化 学 报(Proceedings of the CSU-EPSA)，2010，22(2)：129-133.

[13]Kundur P．电力系统稳定与控制[M]．北京：中国电力出版社，2002．

聂永辉(1970-)，男，讲师，研究方向为信号处理、非线性系统理论在电力系统中的应用。Email:yonghui_n@ yahoo.com.cn

荣令玉(1969-)，男，工程师，主要从事发电运行工作。Email:yonghui_n@ yahoo.com.cn

张立艳(1986-)，女，助理工程师，主要从事电力系统继电保护方面的工作。Email:diaolingheye@ 163.com

LowFrequencyOscillationAnalysisUsingMathematicalMorphologyandESPRIT

NIE Yong-hui1，2， RONG Ling-yu3， ZHANG Li-yan4

(1.Academic Administration, Northeast Dianli University, Jilin 132012, China；2.Electrical Engineering College, Xi'an Jiaotong University, Xi'an 710049, China;3.Operation Department, Huaneng Jiutai Power Plant, Jilin 130501, China;4.Tongchuan Power Supply Bureau, Shanxi Electric Power Company,Tongchuan 727100, China)

To accurately identify power system low frequency oscillation mode parameters, the paper proposes a new approach based on mathematical morphology (MM) and total least squares-estimation of signal parameters via rotational invariance technique (TLS-ESPRIT). Firstly, the measured low frequency oscillation signals with noise will be filtered with the morphological filter based on the principle of MM, which effectively removes noise and improves the identification accuracy. And Then the low frequency oscillation parameters can be obtained through TLS-ESPRIT, which divide a signal into signal subspace and noise subspace. And then the reduced-order model and dominant mode obtained greatly reflects the low oscillation characteristics .This can help to analyze the power system oscillation characteristics and devise power system damping controller. Numerical simulation shows the feasibility and effectiveness of the proposed approach.

low frequency oscillation； parameter identification； total least squares-estimation of signal parameters via rotational invariance technique(TLS-ESPRIT)； mathematical morphology； dominant mode

TM711

A

1003-8930(2012)06-0123-05

2012-01-04；

2012-04-02