径向基神经网络在非线性非定常气动力建模中的应用研究

史志伟，王峥华，李俊成

（南京航空航天大学 航空宇航学院，江苏 南京210016）

0 引 言

传统的气动力建模方法是根据物理机理分析、实验观测等来建立气动力与飞行状态之间的数学关系式，如代数模型、阶跃响应模型、状态空间模型、微分方程模型等。这些方法对线性系统的描述已经非常准确有效，而对于非线性系统则有局限性。随着人工智能技术的发展，模糊逻辑与神经网络方法在非线性非定常气动建模中得到了一定应用，它将气动力的建立过程看作“黑箱”或“灰箱”问题，“黑箱”模型本身作为系统的一种模型，不需要建立有明确表达式的数学模型。这样建立的模型具有强大的自学习功能，能够学习适应不确定性系统的动态特性。由于所有定量或定性的信息都分布储存于网络内，所以有很强的鲁棒性和容错性［1－3］。

本文依据南航NH－2风洞中某飞机模型大迎角大振幅单自由度偏航、滚转及偏航－滚转耦合的谐波、阶跃运动实验数据，采用径向基神经网络，利用其能够充分逼近任意复杂的非线性映射的能力，通过调整网络内部连接权值和阀值，使网络输出逼近实际系统的输出，以此来研究人工神经网络描述非线性非定常气动力特性的能力。

1 RBF神经网络

RBF神经网络是一种前向神经网络，它能够以任意精度逼近任意连续函数，且具有逼近精度高、网络规模小、泛化能力好学习速度快和不存在局部最小问题等特点，已经广泛用于系统参数辨识。

RBF网络一般为3层结构，如图1所示。第一层为输入层；第二层为隐含层（径向基层），隐含层具有径向基函数－－通常取高斯型指数函数，隐层神经元个数根据检查目标误差自动增加节点，重复此过程直到达到目标误差或达到最大神经元数为止；第三层为输出层，具有线性激活函数［4］。

RBF网络输入与第k个输出的关系可表示为：

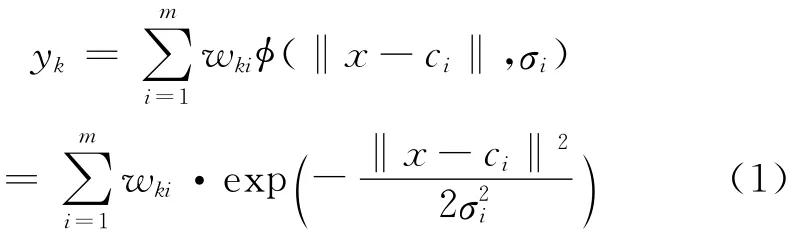
式中，wki为第i个基函数与第k个输出节点的可调连接权值；φi为第i个隐含层的激活函数，也即径向基函数；m为隐含层的节点数。构造和训练RBF神经网络就是要使它通过学习，确定出每个隐层神经元基函数的中心ci、基函数的扩展常数（Spread）或宽度σi以及隐层到输出层的连接权值wki这些参数的过程，从而建立所研究系统的输入到输出的映射。

图1 神经网络的结构Fig.1 The structure of RBFNN

可以看出，RBF网络的基本思想是：用RBF（径向基函数）作为隐单元的“基”构成隐含层空间，这样就可以将输入矢量直接（即不需要通过权值连接）映射到隐空间。当RBF的中心点确定以后，这种映射关系也就确定了。而隐含层空间到输出空间的映射是线性的，即网络的输出是隐单元输出此处的对可调参数的线性加权和。所以，从总体上看，网络由输入到输出的映射是非线性的，而网络输出对可调参数而言却又是线性的。这样网络的权值就可由线性方程直接解出，从而大大加快学习速度并避免局部极小问题。

2 风洞实验

2.1 实验设备

本文实验在南京航空航天大学NH－2低速风洞中进行。图2为动态试验台结构，系统由模型支撑机构、振荡驱动机构、运动控制机构和数据采集处理系统组成。支撑机构运动的规律由计算机通过液压传动机构来控制，因此，其运动可按所需的任意规律变化。图中角度编码器③和⑧可分别测量模型运动的偏航角ψ和滚转角φ。实验时，模型绕飞机体轴X和Y轴同时转动，偏航角与滚转角的运动规律分别为：ψ＝ψ0＋ψmcos2πft；φ＝φ0＋φmcos2πft。当支撑迎角为θ时，对两系统协调控制偏航、滚转角速度满足tanθ＝wy／wx＝，可以实现模型绕速度轴的偏航滚转耦合运动，并保证耦合运动时其两个单自由度的缩减频率相等，与实际飞行情况一致。

由角度编码器测得的模型偏航和滚转运动角度ψ和φ，经过角度转换可得到模型的迎角和侧滑角［5］。

图3所示为模型支撑机构和飞机模型照片。实验时模型采用尾支撑，并保证模型重心、天平校心、模型旋转中心三心重合。

图2 动态实验台示意图Fig.2 The chart of test apparatus

图3 动态实验台和模型照片Fig.3 The photo of test apparatus and model

2.2 数据采集和处理

数据采集通过一杆式六分量应变天平来实现。由于测量数据是在模型作快速往返运动情况下采集得到的，大迎角气流分离引起的流动不重复性，以及模型作高频摆动时的惯性力和气流分离后非定常涡流引起的结构振动的影响，造成测量数据离散性很大，乃至有用的信号淹没在背景噪声之中，而无法获得准确的测量结果。因此，除了数据采集时采用10Hz低通滤波器外，另外设计了数字滤波软件，以减少实验数据的观测噪声。

3 横航向气动力建模和验证

3.1 横航向谐波运动建模

神经网络建模数据来自于飞机模型支撑迎角为40°时，不同强迫振荡频率下的大振幅静态、动态实验数据。实验风速V＝25m／s，模型展长l＝0.75m。模型的动态实验频率分别是0.1Hz～0.7Hz，对应的缩减频率k＝2πf·l／V分别为0.019、0.038、0.057、0.075、0.094、0.113、0.132。其中部分频率下的数据没有用于模型训练，而是作为模型的验证数据。

在数据处理上，训练样本数据输入变量进行归一化处理作为RBF神经网络的输入，这样有利于加快神经网络的收敛速度。此外，通过程序选择出较优的神经网络训练的扩展常数值，有助网络的拟合和泛化。

以横航向运动的滚转力矩系数（偏航力矩系数）为例，建模输入变量采用机构运动时的偏航角ψ、滚转角φ、缩减频率k、模型支撑迎角α。具体各模型变量的形式如下：单自由度偏航运动的偏航力矩系数My＝f（α，ψ，k）；单自由度滚转运动的滚转力矩系数Mx＝f（α，φ，˙φ，k）；偏航滚转耦合运动Mx，y＝f（α，ψ，φ，˙φ，k）。

图4、图5为单独偏航运动情况下，所建立模型的预测结果与训练数据和验证数据的对比。图6、图7为单独滚转运动情况下，所建立模型的预测结果与训练数据和验证数据的对比。图8、图9为偏航滚转耦合运动情况下，所建立模型的预测结果与训练数据和验证数据的对比。

图4 单独偏航运动的模型预测结果与训练数据的比较（f＝0.3Hz）Fig.4 Comparison of teaching data and simulation results of yawing unsteady model（f＝0.3Hz）

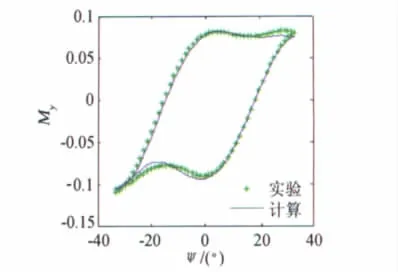
图5 单独偏航运动的模型预测结果与验证数据的比较（f＝0.5Hz）Fig.5 Comparison of validating data and simulation results of yawing unsteady model（f＝0.5Hz）

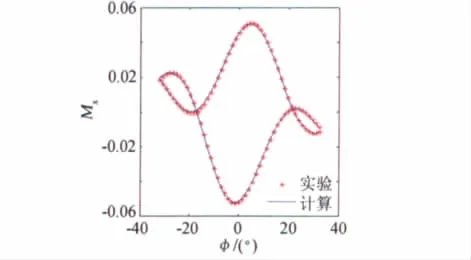
图6 单独滚转运动的模型预测结果与训练数据的比较（f＝0.3Hz）Fig.6 Comparison of teaching data and simulation results of rolling unsteady model（f＝0.3Hz）

图7 单独滚转运动的模型预测结果与验证数据的比较（f＝0.5Hz）Fig.7 Comparison of validating data and simulation results of rolling unsteady model（f＝0.5Hz）

从仿真结果来看，利用训练样本数据建立的RBF神经网络模型，其仿真计算得到的Mx、My力矩系数与训练数据和验证数据几乎重合，证明了RBF神经网络对非线性气动力很强的逼近能力。由于验证数据与所建立的模型预测结果符合的很好，因此某些中间频率的实验值能用其他实验数据建立的模型计算结果来替代。这也就是说用神经网络方法建立模型所需风洞实验次数可以减少，因此可以减少风洞实验的时间和成本。

图8 偏航滚转耦合运动的模型预测结果与训练数据的比较（f＝0.5Hz）Fig.8 Comparison of teaching data and simulation results of yawing－rolling unsteady model（f＝0.5Hz）

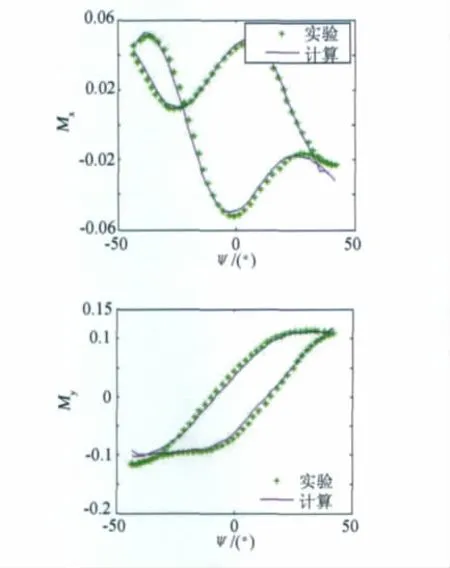
图9 偏航滚转耦合运动的模型预测结果与验证数据的比较（f＝0.3Hz）Fig.9 Comparison of validating data and simulation results of yawing－rolling unsteady model（f＝0.3Hz）

3.2 阶跃运动仿真验证

利用前面单独建立的不同运动情况下的气动力模型，可以进一步仿真计算模型阶跃运动时的气动力特性，从而进一步检验所建立模型的适应性和实用性。

由于气动模型中输入变量k是指谐波运动的缩减频率，但阶跃运动中并不存在实际的缩减频率k，因此在仿真计算过程中需要给出一等效的缩减频率。等效缩减频率的计算如下［6］：

其中ω和其他参数最小化目标函数来计算得到。

n为假定的计算采用的一个数据长度。图10给出偏航滚转耦合运动时计算得到的等效缩减频率。

图10 偏航滚转耦合阶跃运动的等效缩减频率Fig.10 Curves of the equivalent reduced frequency of yawing－rolling ramp motion

利用单独建立的不同运动情况下的径向基神经网络模型，仿真计算阶跃运动时的气动力数据，并与阶跃运动的实验数据进行比较，结果见图11－图13。

计算结果表明，仿真的结果能够较好地拟合实验数据，尤其阶跃上升段和下降段拟合得较好，运动的变化趋势也能模拟出来。但是在中间运动停止阶段拟合的精度不是很高，出现了“平台”，这是因为在仿真计算中的等效缩减频率k均为0而导致的。而实际运动过程中由于受到非定常气动力迟滞效应的影响，这里的数据有一些变化。总体而言，阶跃运动验证了RBF网络模型的准确性和适用性，用它来进行非线性非定常气动力建模还是可行的。

图11 单独偏航阶跃运动My的预测结果与实验结果比较Fig.11 Comparison of test data and simulation results of yawing ramp motion

图12 单独滚转阶跃运动Mx的预测结果与实验结果的比较Fig.12 Comparison of test data and simulation results of rolling ramp motion

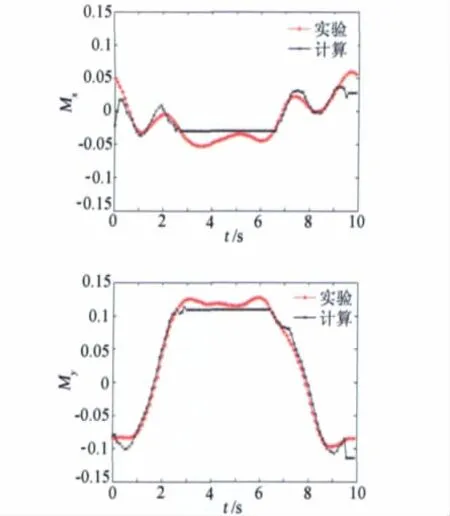
图13 偏航－滚转耦合阶跃运动Mx、My的预测结果与实验结果的比较Fig.13 Comparison of test data and simulation results of yawing－rolling ramp motion

4 结 论

本文讨论了非线性非定常气动力的径向基神经网络建模方法，利用飞机大迎角大振幅运动的单独俯仰、单独偏航、单独滚转和偏航－滚转耦合谐波运动实验数据验证了模型的有效性。说明利用径向基神经网络模型可以有效地对一些高度非线性的气动力问题进行建模；并且用神经网络方法建立模型可以减少风洞实验次数，从而减少风洞实验时间、降低成本。通过建立单偏、单滚及耦合运动的综合模型用于阶跃运动的仿真，结果表现出了较好的逼近能力，进一步验证了RBF神经网络模型的实用性和适应性，说明径向基神经网络在处理多变量、非线性、非定常气动力问题时是一种有效的方法。

［1］LINSE D J，STENGEL R F.Identification of aerodynamic coefficients using computational neural networks［R］.AIAA paper 92－0172，1992.

［2］JAME E S，KAMRAN ROKHSAZ.Some applications of ANN in modeling of nonlinear aerodynamics［R］.AIAA 97－0338，1997.

［3］龚正，沈宏良.非定常气动力的结构自适应神经网络建模方法［J］.飞行力学，2007，25（4）：13－16.

［4］丛爽.神经网络理论与应用［M］.中国科学技术大学出版社，合肥，2009.

［5］黄达，吴根兴.飞机偏航－滚转耦合运动非定常空气动力实验［J］.南京航空航天大学学报，2005，37（4）：408－411.

［6］WANG ZHONG－JUN，LAN C E.Unsteady aerodynamic effets on the flight characteristics of an F－16XL configuration［R］.AIAA 2000－3910，2000.