圆柱跨声速绕流中的激波／湍流相互作用大涡模拟研究

许常悦，王从磊，孙建红

（南京航空航天大学 航空宇航学院，江苏 南京210016）

0 引 言

激波／湍流相互作用问题是可压缩湍流研究领域中的挑战性问题，与其相关的机理认识已成为工业应用上必须解决的问题，并得到了广泛的研究［1－4］。该类问题的研究中常选用一些规范构型作为研究对象，如平板、斜坡、鼓包、翼型和柱体，等等。研究的复杂性与构型有关［3］，弯曲壁面会产生复杂的流场结构。对于多数实际流动而言，激波／湍流相互作用常发生在弯曲壁面上，这与该处的湍流边界层中存在较大的压力梯度有关［4］。研究弯曲壁面物体绕流中的激波／湍流相互作用问题受到了广泛的关注，尤其是圆柱跨声速绕流。

目前已有一些关于圆柱跨声速绕流的实验和数值研究。Macha［5］、Murthy＆Rose［6］和 Rodriguez［7］实验研究了雷诺（Re）数约为105的圆柱跨声速绕流问题，展示了此类流动中的阻力上升现象和激波结构。近年来，Riserda＆Leal［8］采用有限体积方法求解二维可压缩Navier－Stokes方程，研究了来流马赫数为0.8的圆柱绕流问题，主要分析了柱体的非定常受力和近场流场结构。在之前的工作中［9－10］，我们已经对来流马赫数对圆柱跨声速绕流的影响进行了研究，并分析了不同流动状态下的局部超声速区形成机制和剪切层的不稳定性过程，然而关于大尺度的激波运动和非定常湍流剪切层的湍流特性等问题并未详细研究，这正是本文的研究目的。

在当前的计算流体力学中，雷诺平均Navier－Stokes方程（RANS）方法、直接数值模拟（DNS）方法和大涡模拟（LES）方法是主要的湍流研究手段。RANS方法在计算激波／湍流相互作用问题时无法给出可靠的结果，这是由于RANS方法不能正确捕捉流动分离和再附过程，并且无法预测低频的激波运动。DNS方法能够再现湍流中各种尺度的涡结构。在高Re数流动中，湍流尺度有很宽的谱域，只有网格数达到Re3（包括时间维）的量级，才能有足够的时空分辨能力。因此，目前的计算条件下DNS方法还只能研究Re数较低的湍流问题［11］。LES方法直接计算湍流中较大尺度的涡，而将动力学意义不大的小涡用亚格子（SGS）模型来模拟，因此它可以反映较多的湍流信息，具有较好的普适性。近年来，LES方法已经被成功应用于激波／湍流相互作用问题的研究［3－4］，故本文采用 LES方法作为研究手段。

1 数值计算方法

1.1 控制方程

当前采用的控制方程为守恒型的三维Favre滤波可压缩Navier－Stokes方程。方程的无量纲化采用来流密度ρ∞、温度T∞、速度U∞和圆柱直径D作为特征量。无量纲的控制方程可以写成如下形式：

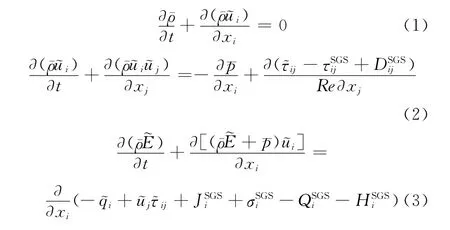
其中，顶标“－”和“～”分别表示空间滤波和Favre滤波，即＝／。变量ρ、ui、p和E分别为密度、速度分量、压力和总能。扩散项通过下面式子给出：

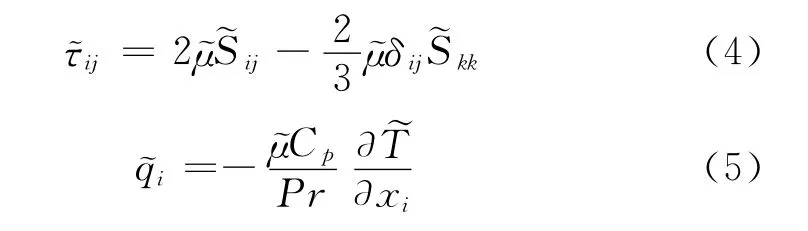
这里，μ为分子粘性系数，Cp为定压比热比，Pr为Prandtl数，Sij＝（∂ui／∂xj＋∂uj／∂xi）／2为应变率张量。此外，理想气体方程和计算μ的Sutherland公式被采用。

方程（2）和（3）中的SGS未封闭项的定义如下：

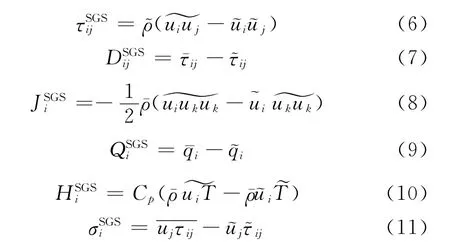
1.2 动力SGS模型

控制方程经过滤波后会产生一些SGS未封闭项，需要进行模化。由于对能量方程的影响较小，该项可以忽略；粘性应力非线性项和热通量非线性项Q经常被忽略。下面对、H和J未封闭项的模化过程进行详细介绍。

Yoshizawa［12］针对弱可压缩湍流，提出了一种多尺度直接相互作用的近似模型：SGS应力项τ反对称部分τ－δijτ／3采用Smagorinsky模型进行模化，而对称部分τ则单独模化：

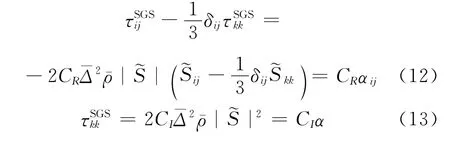
其中，｜｜＝＝（ΔxΔyΔz）1／3为滤波宽度。CR和CI为模型系数，需要通过二次滤波动态求解。Lilly［13］建议采用最小二乘法获得模型系数：

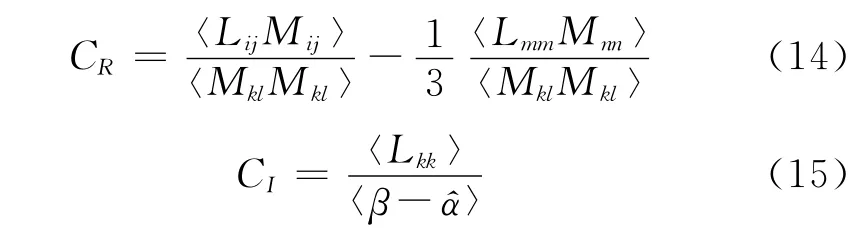
其中，〈·〉表示局部光滑操作，即采用当地27个网格单元的体积加权平均实现，该方法常被用来提高数值计算的稳定性［14］。Lij、Mij和β的形式分别为：

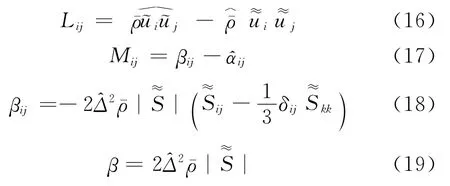
SGS能量项H的模化如下：

其中，＝2｜｜。同模型系数CR和CI，湍流Prandtl数的求法如下：

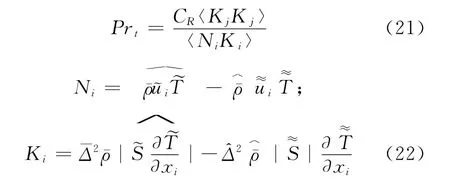
SGS湍流扩散项的模化借鉴Knight等人［15］的做法，即J＝。

1.3 离散格式和边界条件

本文采用有限体积方法求解Favre滤波后的控制方程（1）－（3）。对流项的离散采用二阶的中心－迎风型混合格式。在该混合格式中，中心格式和Roe通量差分裂迎风格式之间的切换，通过一个二进制开关函数Φi＋1／2来实现：

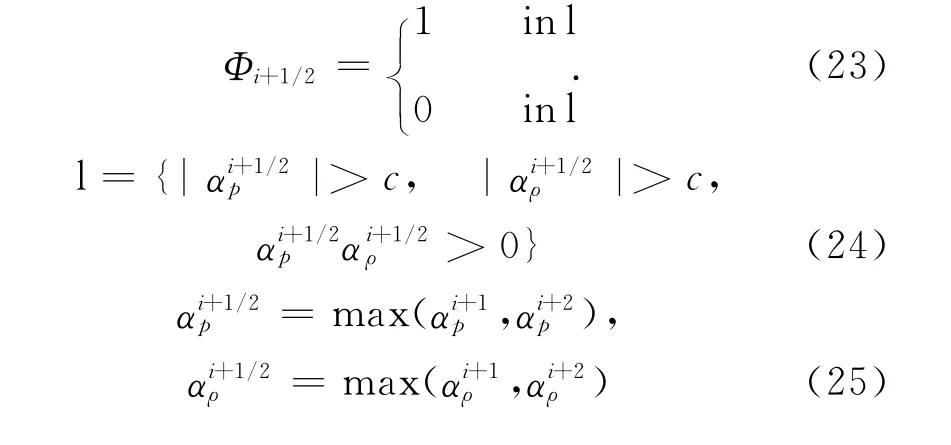
程序中以自由来流为初始条件，远场条件采用基于当地一维Riemann不变量的无反射特征边界，壁面采用无滑移、无穿透的绝热边界条件，展向采用周期性边界条件。

2 计算结果与分析

2.1 计算参数

基于已有的实验研究［5－7］，本文选取的来流马赫数M∞为0.75，基于圆柱直径D的雷诺数为2×105。采用O型计算网格，壁面和激波区附近的局部网格如图1所示，壁面法向最小网格尺度为10－5D。经过仔细测试［9－10］，流向、周向和展向的网格数分别取为513、513和121，径向计算域直径为50D，展向长度为4D，时间步长为0.00375D／U∞。为了表述方便，对本文的符号作如下说明：〈〉表示时间和展向同时平均，｛｝表示密度加权平均，即｛φ｝＝φ〉／〉；脉动密度和脉动压力为＝－〈〉和＝－〉，脉动速度为＝－｝。

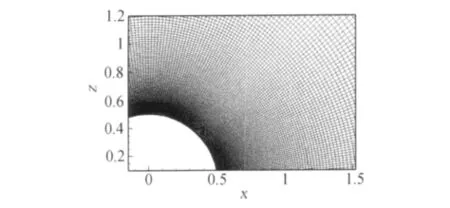
图1 壁面和激波区附近的局部计算网格Fig.1 Local computational grid near the wall and shock region

2.2 计算结果验证

为了验证当前计算结果的可信性，本文和已有实验数据［5－7］进行比较，对比的物理量有壁 面压力〈pw〉、表面摩擦系数〈｜Cf｜〉、压力脉动均方根值p、时均阻力系数〈CD〉t、升力系数均方根值CLrms和涡脱泻Strouhal（St）数。图2给出了沿柱体表面的〈pw〉、〈｜Cf｜〉和变化曲线。表1给出了LES计算结果和实验数据的对比情况。从图2和表1中可以看出，当前LES计算结果和已有的实验数据相符较好，这表明当前的LES计算结果具有较好的可信性。

表1 当前计算结果和实验数据的对比Table 1 Comparison of the present calculated results with the experimental data

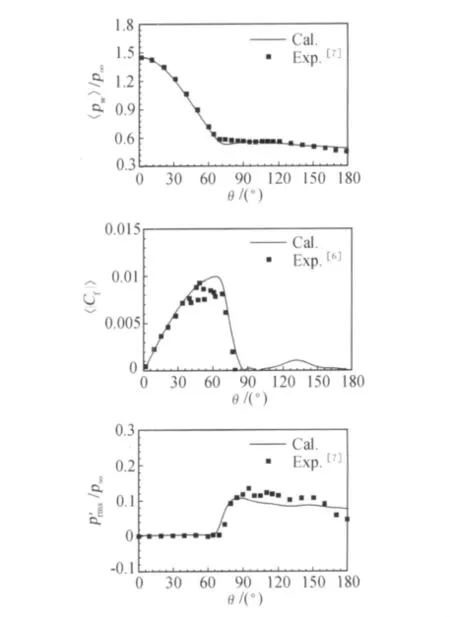
图2 沿柱体表面的平均压力〈pw〉（a）、表面摩擦系数〈｜Cf｜〉（b）和压力脉动均方根值（c）分布。这里，θ＝0对应柱体的前缘Fig.2 Distributions of the mean pressure〈pw〉（a），skin friction coefficient〈｜Cf｜〉（b）and root－mean－square value of pressure fluctuationon the cylinder surface（c）.Here，θ＝0increases from the front－point of the cylinder in the clockwise direction

2.3 大尺度激波运动

已有研究结果［7，9－10］表明，当M∞＝0.75时圆柱分离点处会形成一道斜激波。关于翼型表面的激波运动已得到广泛的研究［17］，结果表明存在三种运动模式：正弦类运动（A类）、间歇式运动（B类）和向上游传播类运动（C类）。然而，关于圆柱表面的激波运动模式研究较少。为了定性地分析圆柱表面的激波运动模式，图3给出了不同时刻的瞬时流场图。可以看出，圆柱分离点处的激波在柱体上下表面交替出现，并且向上游传播，这与翼型表面的C类激波运动模式相似。为了获得该激波运动的特征St数，在其运动区内的设置一个探测点P1，如图3（a）所示。图4给出了P1点处的能谱分布，可以看出激波运动的特征St数与涡脱泻St数一致，均为0.19。此外，－5／3次方斜率关系表明当前计算结果达到了湍流的惯性子区［18］。

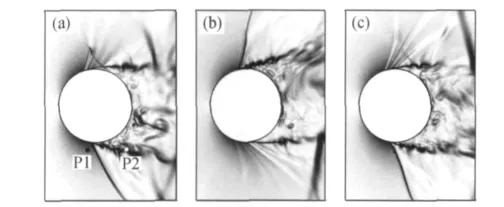
图3 利用密度梯度模‖▽‖表示的激波运动，时间间隔为0.9D／U∞Fig.3 Shock wave motion depicted by the magnitude of density gradient‖▽‖.The time interval is 0.9D／U∞

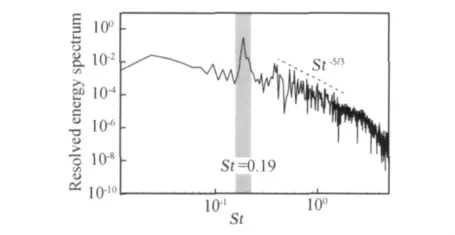
图4 P1点处的能谱曲线。P1点的位置见图3（a）Fig.4 Resolved energy spectrum at probe P1in Fig.3 （a）

图5 基于压力场POD分解的前四个模态空间分布Fig.5 Spatial distributions of first four POD modes based on the pressure fields

为了分析激波运动对流动模态的影响，采用本征正交分解（POD）方法研究流场的主模态。对于一个给定的流动变量f（x，t），POD分析可以确定一族正交函数φj（x），j＝1，2，…，则f在前n个函数上的投影为最

小误差定义为〈‖f－‖2〉，这里分别表示时间平均和L2空间模，aj（t）代表第j个模态随时间变化的系数［19］。图5给出了基于压力场POD分解的前四个模态，实线表示正值，虚线表示负值，30个等值线从－1.5ρ∞增加到1.5ρ∞U。可以看出，mode1和mode3呈现反对称模态，这与柱体分离点处的大尺度激波运动有关；mode2和mode4呈现对称模态，这与柱体尾迹中的涡脱泻现象有关，相似的结论也见于翼型跨声速绕流问题的研究［20］。

2.4 非定常湍流剪切层行为

已有的研究［9－10］主要关注剪切层的不稳定性过程，本文将对剪切层中的压力信号特性和剪切层的湍流特性进行研究。

首先考察的是剪切层中的压力信号特性。为此，在剪切层附近设置一个压力探测点P2，如图3（a）所示。P2点处的压力信号功率谱（PSD）分析如图6所示，可以看出该处的特征St数与涡脱泻St数一致，并且PSD曲线中存在一些特征斜率关系。由于圆柱剪切层的扰动源来自柱体分离点，故剪切层附近的压力信号PSD曲线中呈现出的斜率关系与壁面附近的压力信号一致：低频区的0.4次方斜率关系与边界层外层区域的湍流有关［21］，在低频区向高频区过渡区，边界层对数律区的涡结构会导致－1次方的斜率关系［18］，高频区则呈现－5次方的斜率关系［22］。

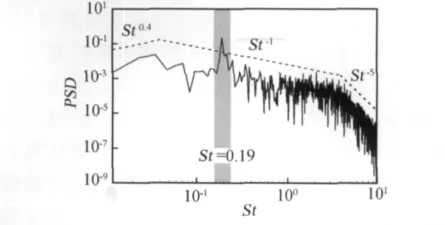
图6 P2点处的压力信号功率谱（PSD）曲线，P2点的位置见图3（a）Fig.6 Power spectral density（PSD）of pressure at P2in Fig.3 （a）

其次，采用象限分解技术［23］研究非定常剪切层的湍流特性。流场中的瞬时流向脉动速度u″和横向脉动速度w″通过采样流场计算得到，并且u″和w″分别采用流向脉动速度均方根值σu和横向脉动速度均方根值σw正则化。图7（a）给出了剪切层区域内P2点处的平均剪切应力｛u″w″｝的象限分解。这里，剪切应力值取为0.01。从图中可以看出，剪切层区域的脉动速度趋于有组织性。为了分析剪切应力的演化特性，本文计算了瞬时的剪切应力角ψ，其定义为ψ＝tan－1（w″／u″）。ψ＜0对应象限分解中的第二、四象限；ψ＞0对应象限分解中的第一、三象限；ψ＝0表示仅存在流向脉动速度u″。图7（b）给出了P2点处的瞬时剪切应力角的概率密度函数（PDF）分布。这里，N表示采样流场数目，NT表示总的采样流场数目。可以看出，P2点处的剪切应力角ψ趋于0，这表明该处的脉动速度以流向脉动速度为主。

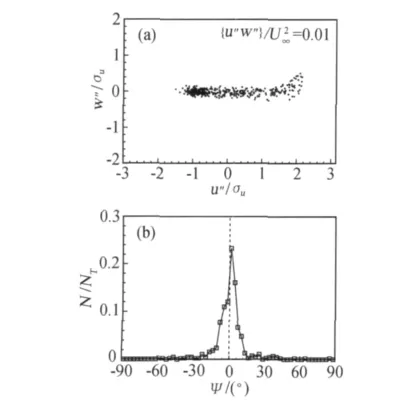
图7 P2点处的剪切应力象限分解（a）和瞬时剪切应力角概率密度函数分布（b），P2点的位置见图3（a）Fig.7 Shear stress quadrant decomposition（a）and PDF of the shear－stress angle（b）at probe P2in Fig.3 （a）

最后，为了深入分析剪切层中的湍流特性，考察了正应力各向异性比例和湍流结构参数沿剪切层的变化，如图8所示。这里，分析的正应力各向异性比例有流向－展向比（σu／σw）2和横向 －展向比（σv／σw）2。从图8（a）中可以看出，流向－展向比的值沿剪切层从45迅速衰减，而横向－展向比的值几乎为0，这表明剪切层中的流向正应力占主导地位，这与前文象限分解得出的结论一致。分析的湍流结构参数也为两个比例关系，即－｛u″w″｝／k和Ruw＝－｛u″w″｝／（σuσw）。这里，k＝（σ2u＋σ＋σ）／2为湍动能，Ruw为剪切应力相关系数。图8（b）给出了－｛u″w″｝／k和Ruw沿剪切层的变化，可以看出－｛u″w″｝／k沿剪切层增加，而Ruw沿剪切层衰减，这与剪切层中的大尺度结构组织性减小有关［24］。

图8 正应力各向异性比例（a）和湍流结构参数（b）沿剪切层变化Fig.8 Evolution of the normal shear stress anisotropy ratio（a）and of turbulence structure parameter（b）along the shear layer

3 结 论

本文采用大涡模拟方法研究了圆柱跨声速绕流中的激波／湍流相互作用问题，分析了大尺度的激波运动、剪切层中的压力信号特征和湍流特性。来流马赫数M∞取为0.75，基于圆柱直径D的雷诺数为2×105。通过对计算结果的分析和讨论有如下结论：（1）圆柱分离点处出现一道向上游传播的斜激波，并且运动的St数与涡脱泻St数一致；（2）分离点处的激波运动导致流场中出现反对称的流动模态；（3）圆柱剪切层中的压力信号PSD曲线中存在0.4、－1和－5次方的斜率关系，剪切层中的脉动速度以流向脉动速度为主，并且沿剪切层的大尺度结构组织性减小。

［1］DECK S.Numerical simulation of transonic buffet over a supercritical airfoil［J］.AIAAJ.，2005，43（7）：1556－1566.

［2］PIROZZOLI S，GRASSO F.Direct numerical simulation of impinging shock wave／turbulent boundary layer interaction atM＝2.25［J］.Phys.Fluids，2006，18（6）：065113.

［3］LOGINOV M S，ADAMS N A，ZHELTOVODOV AA. Large－eddy simulation of shock－wave／turbulentboundary－layer interaction［J］.J.FluidMech.，2006，565：135－169.

［4］SANDHAM H D，YAO Y F，LAWAL A A.Large－eddy simulation of transonic turbulent flow over a bump［J］.Int.J.HeatFluidFlow，2003，24（4）：584－595.

［5］MACHA J M.Drag of circular cylinders at transonic Mach numbers［J］.J.Aircraft，1977，14（6）：605－607.

［6］MURTHY V S，ROSE W C.Detailed measurements on a circular cylinder in cross flow［J］.AIAAJ.，1978，16（6）：549－550.

［7］RODRIGUEZ O.The circular cylinder in subsonic and transonic flow［J］.AIAAJ.，1984，22（12）：1713－1718.

［8］MISERDA R F B，LEAL R G.Numerical simulation the unsteady aerodynamic forces over a circular cylinder in transonic flow［R］.AIAA Paper 2006－1408，2006.

［9］XU C Y，CHEN L W，LU X Y.Effect of Mach number on transonic flow past a circular cylinder［J］.ChineseSci.Bull.，2009，54（11）：1886－1893.

［10］XU C Y，CHEN L W，LU X Y.Numerical investigation of shock wave and turbulence interaction over a circular cylinder［J］.Mode.Phys.Lett.B，2009，23（3）：233－236.

［11］MOIN P，MAHESH K.Direct numerical simulation：a tool in turbulence research［J］.Annu.Rev.Fluid Mech.，1998，30：539－578.

［12］YOSHIZAWA A.Statistical theory for compressible turbulent shear flows，with the application to subgrid modeling［J］.Phys.Fluids，1986，29（7）：2152－2164.

［13］LILLY D K.A proposed modification of the Germano subgrid scale closure method［J］.Phys.Fluids，1992，4（3）：633－635.

［14］MOIN P，SQUIRES K，CABOT W，et al.A dynamic subgrid－scale model for compressible turbulence and scalar transport［J］.Phys.Fluids，1991，3（11）：2746－2757.

［15］KNIGHT D，ZHOU G，OKONG＇O N，et al.Compressible large eddy simulation using unstructured grids［R］.AIAA paper 1998－0535，1998.

［16］SWANSON R C，TURKEL E.On central－difference and upwind schemes［J］.J.Comput.Phys.，1992，101（2）：292－306.

［17］TIJDEMAN H，SEEBASS R.Transonic flow past oscillating airfoils［J］.Ann.Rev.FluidMech.，1980，12：181－222.

［18］NA Y，MOIN P.The structure of wall－pressure fluctuations in turbulent boundary layers with adverse pressure gradient and separation［J］.J.FluidMech.，1998，377：347－373.

［19］BERKOOZ G，HOLMES P，LUMLEY J L.The proper orthogonal decomposition in the analysis of turbulent flows［J］.Annu.Rev.FluidMech.，1993，25：539－575.

［20］BOURGUET R，BRAZA M.Reduced－order modeling for unsteady transonic flows around an airfoil［J］.Phys.Fluids，2007，19（11）：111701.

［21］PANTON R L，LINEBARGER J H.Wall pressure spectra calculations for equilibrium boundary layers［J］.J.FluidMech.，1974，65：261－287.

［22］BLAKE W K.Mechanics of flow－induced sound and vibration［M］.New York：Academic Press，1986.

［23］WALLACE J M，ECKELMANN H，BRODKEY R S.The wall region in turbulent shear flow［J］.J.Fluid Mech.，1972，54：39－48.

［24］HERRIN J L，DUTTON J C.The turbulence structure of a reattaching axisymmetric compressible free shear layer［J］.Phys.Fluids，1997，9（11）：3502－3512.