基于5阶精度格式WCNS-E-5的p-multigrid方法研究
王新光, 毛枚良,, 邓小刚, 涂国华
(1.中国空气动力研究与发展中心,四川 绵阳621000;2.空气动力学国家重点实验室,四川 绵阳621000)
0 引 言
高阶精度差分算法同目前成熟的二阶精度算法相比,普遍存在收敛速度慢等问题,成为高精度算法推广应用的瓶颈之一。为了克服这一困难,参照多重网格算法的思想,提出了一种所谓的p-multigrid方法。众所周知,多重网格方法(multigrid)的实质是为了快速获得精细网格上的计算结果,在迭代过程中,引入与精细网格存在特定关系的粗网格上的计算过程技术。类似地,p-multigrid方法的实质是为了稳定快速地得到高精度算法的计算结果,在迭代过程中,引入低阶精度算法的计算过程技术。
p-multigrid方法是由Rönquist等首先提出的。随后在间断有限元中得到了广泛的应用,Maday等[1]分析了p-multigrid方法用于拉普拉斯方程的稳定性,Bassi和 Rebay[2]率先将p-multigrid方法用于求解一维的欧拉方程。而Joseph等[3]建立了一套快速低存储量的p-multigrid方法,并将其用于求解可压缩欧拉方程。Krzysztof等[4]将p-multigrid方法和单元线光滑器(element line smoother)结合,建立了一个新的算法,并将其用于求解可压缩的NS方程,结果表明这种方法可以明显减小计算时间,加快收敛速度。以上这些都是p-multigrid方法在间断有限元中的应用。最近几年,Kris Van Den Abeele等[5]将p-multigrid成功用于一维谱体积法(Spectral Volume Method)中,Aleksundar等[6]将其用于RPM(Recursive Projection Method)中,都可以减少计算时间加快收敛。以上这些都证明了p-multigrid方法在加速收敛等方面具有很大的潜力,但从检索的文献中还没有发现p-multigrid算法用于有限差分中。
由于差分方法和间断有限元方法的构造思想不同:有限元方法是通过不同精度的基函数来达到不同的精度,各阶导数是直接计算的,而有限差分方法中,并没有这样的基函数,而各阶导数是由变量分布通过差商得到的。因此,差分方法的p-multigrid方法和间断有限元方法的p-multigrid方法是不同的。在多重网格法中,使用一种亏损修正法(defect-correction),实现了将二阶精度算法结果修正到四阶精度。
WCNS-E-5格式为5阶精度的非线性耗散紧致显式格式,是邓小刚研究员等构造的高精度格式之一[7-8],具有良好的耗散、色散特性,在 Euler、N-S和RANS方程等一系列的数值考核试验中,WCNS格式都表现了良好的性能[9-10]。本文的目标是,基于WCNS-E-5格式和上述亏损修正法的基本思想,通过引入1阶精度迎风格式和3阶精度非线性加权差分格式,设计了一类p-multigrid方法,通过典型算例,考察了不同方式的p-multigrid方法对计算过程收敛速度的影响。
1 基本理论
1.1 空间离散
考虑标量双曲型线性方程:

此处,c>0为常数。对于网格间距h的均匀网格,式(1)的半离散方程:

式(2)中一阶导数的离散采用3种精度的格式进行离散,一阶迎风格式
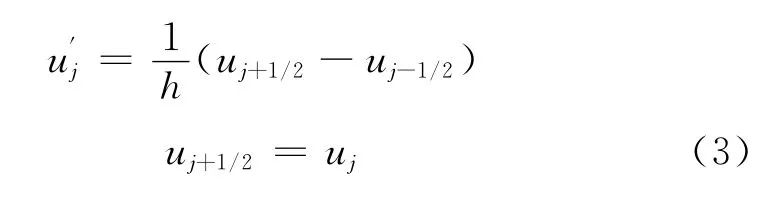
最优3阶精度的加权格式

最优5阶精度的 WCNS-E-5格式其中,权值的定义为:
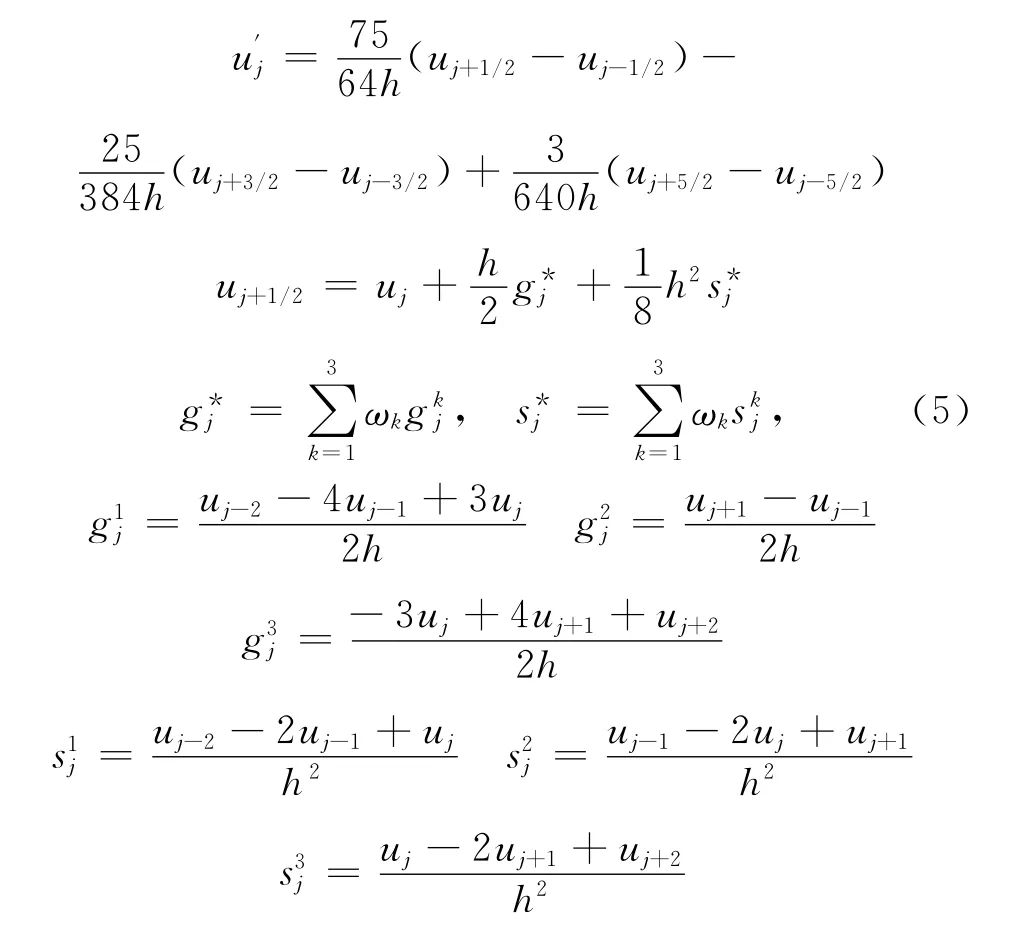

其中ε=10-10是为避免分母为零而加的小量。ISk为模板的光滑性度量。
权值设计目标是:在光滑的流动区,权值应逼近最优值,即可以达到格式的最优精度;在间断附近,含有间断的模板被赋予的权值接近于零,这样就避免了跨间断插值,消除了数值波动。
1.2 P-multigrid
基于上述三种精度格式和p-multigrid方法的思想,类似于多重网格方法(即p-multigrid方法中最高精度格式相对于多重网格方法中的最密的网格),可以构造算法为5阶精度的多种迭代循环方法。图1给出了典型的3种循环方法V、W、Saw,图2和图3分别给出了组合循环方法Pre_V和FMG。图中圆点表示使用了对应精度的格式。

图1 在三重精度上的V、W、S循环Fig.1 V,S ,W-circle based on three different schemes

图2 在三重精度上的Pre_V循环Fig.2 Pre_V-circle based on three different schemes
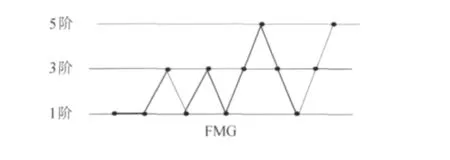
图3 在三重精度上的FMG循环Fig.3 FMG based on three different schemes
下面基于三阶、五阶格式的小V循环的计算过程叙述如下:
1)利用五阶格式迭代ν1步,计算得到一个初始解u0;
2)利用三阶和五阶的加权格式分别计算得到RHS3(u0)和RHS5(u0),计算驱动源项:F=RHS5(u0)-RHS3(u0);
3)将u*0→u*;
4)利用三阶格式计算RHS3(u*),再利用驱动源项F计算:RHS*=F+RHS3(u*),并利用这个RHS*得到一个新的u*1;
5)重复4),迭代ν2步后得到的结果u*ν2;
6)将u*ν2→ui,回到1),完成了一个循环。
上述过程中,随着残差逐渐收敛到零,使得上述过程中ui=u*i=u*,则使得其中的第四步:RHS*=F+RHS3(u*)=RHS5(u*),最终结果得到的是一个五阶精度算法的结果。因此,对于本文给出的p-multigrid方法,计算收敛后的结果是 WCNS-E-5格式的解。
2 算例考察
2.1 一维粘性Burgers方程
这个算例的主要目的是考察图1中的V循环,在各个精度上选择不同的步数,使用不同初值的计算收敛情况。对于非线性Burgers'方程:
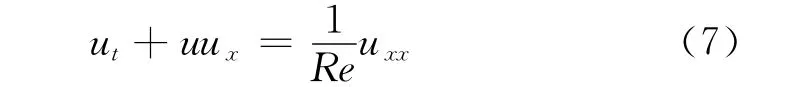
其精确解为:

其中通过下式通过迭代求解:

计算条件:Re=25,u|x=0,u|x=1=-1。
表1给出了图1中V循环在各层精度上使用不同步数的三种循环,图4给出了四种不同的初值。图5为由不同的初值得到的收敛结果,可见它们只与算法精度相关,表2进一步定量地展示了计算结果同算法的关系,所采用的V循环计算结果同 WCNS-E-5格式的一致,但计算所消耗的CPU时间接近于3阶精度格式,比5阶精度格式减少约30%,图6全面展示了算法和初值对收敛速度的影响,p-multigrid方法的收敛速度均比 WCNS-E-5格式的要快,同时,初值对收敛速度存在明显的影响。
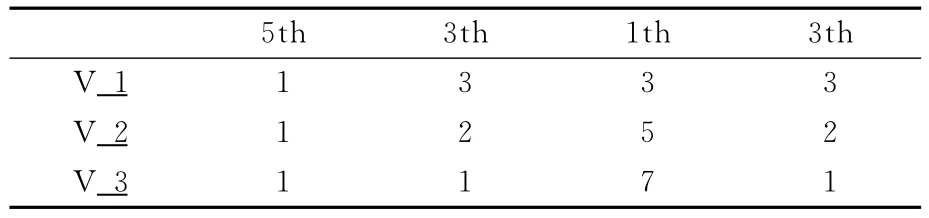
表1 三种不同的V循环Table 1 Three different V-circles
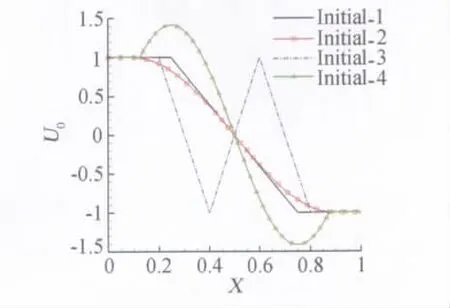
图4 四种不同的初值Fig.4 Four different initial values
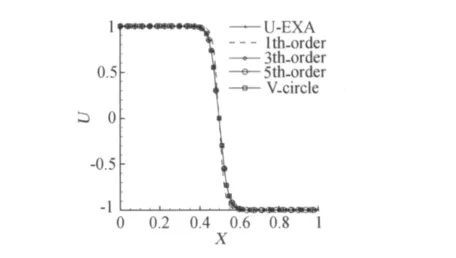
图5 精确解和数值解的比较Fig.5 Comparison of exact solution and numerical solution
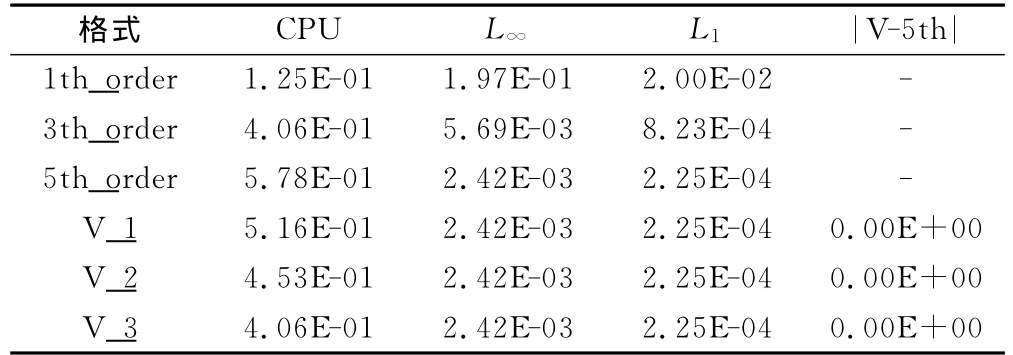
表2 Initial_1的结果比较Table 2 Comparison of different initial_1's solution
2.2 二维无粘圆柱
采用图7所示的网格(O型网格:128×33,物面距离0.001,远场取到20倍直径),计算条件为M=0.3的无粘圆柱绕流。
在不可压假设下,低速无粘圆柱绕流的壁面压力系数的理论解为:
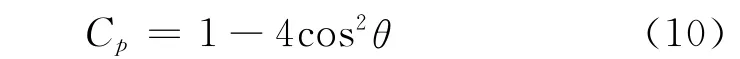
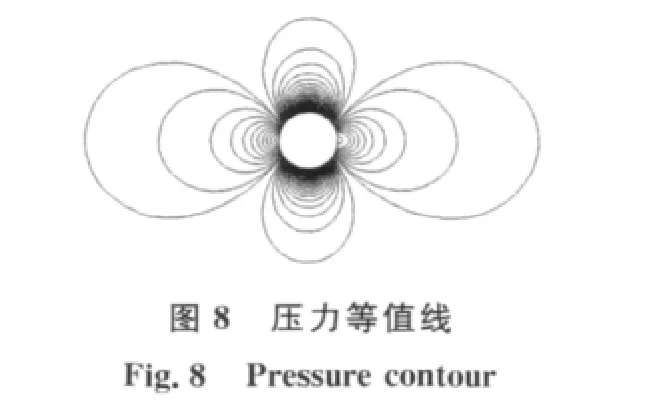
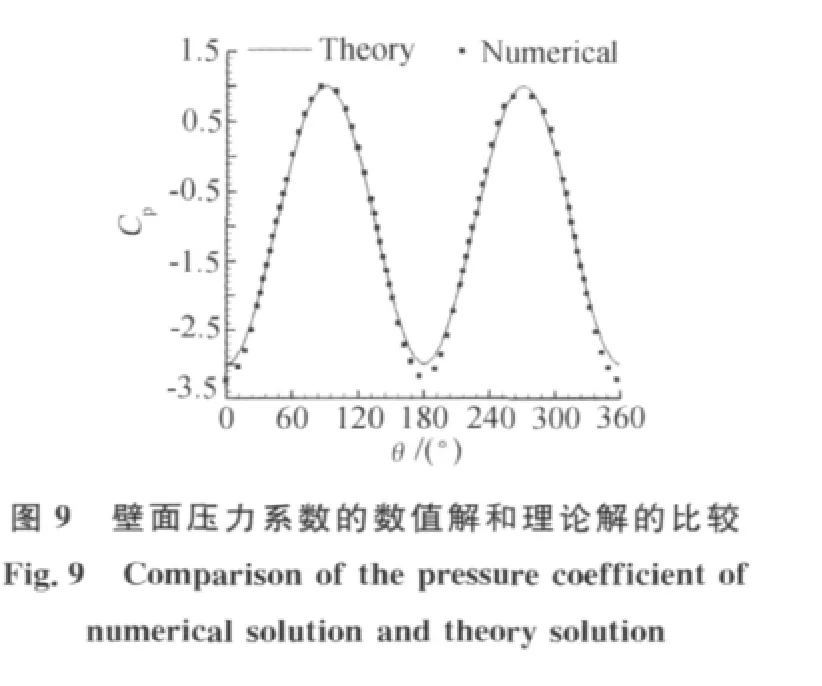
其中θ角表示图7中以其中的粗线为基准,逆时针旋转的角度,前驻点处θ=90°。图8给出了流场的压力等值线。图9给出了数值解和理论解的比较,考虑到可压缩性效应,两者一致性良好。
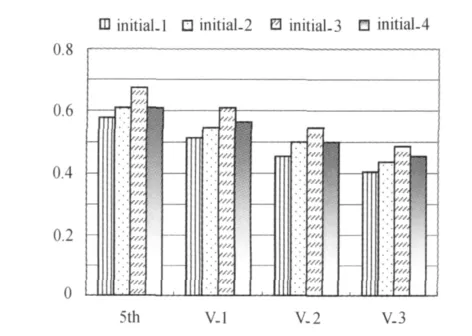
图6 不同算法不同初值消耗的CPU时间的柱状图Fig.6 Bar chart of CPU time of different schemes and different initials

通过无粘圆柱来研究图1和图2所示的五种不同循环的效率以及脉动范围的大小。由于在无粘圆柱的计算中后驻点压力收敛速度最慢,可以通过后驻点来观察圆柱的收敛情况,图10展示了各种算法给出的后驻点压力收敛情况,使用p-multigrid的各种循环和五阶格式相比收敛速度更快,脉动范围更小。图11给出了壁面压力最大偏差(瞬时值与5阶精度方法的收敛值之差)迭代的演化情况,Pre_V和FMG方法的收敛速度要明显的快于V、S、W循环,主要是由于这两种循环,可以看做是在V循环开始之前,使用三阶格式和一阶格式计算了一个较好的初场。
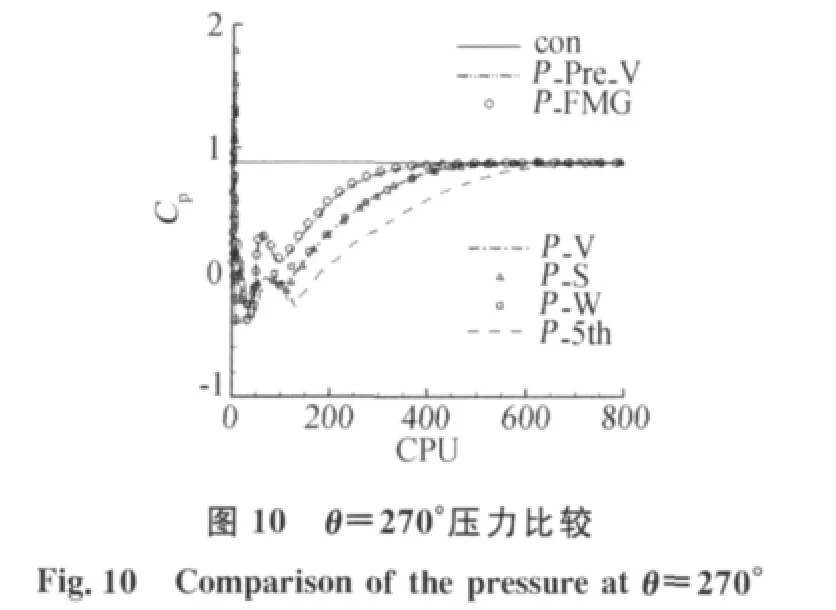

同时从图10、图11中可以看到在计算的初期pmultigrid方法可以有效地加速收敛,但是随着流场逐渐收敛,在计算的后期p-multigrid方法加速收敛的效果不再明显。
2.3 NACA0012翼型
采用图12中所示的网格(C型网格:121×50,物面距离0.001)。计算条件为M=0.3,Re=30.0,攻角α=0.0°。图13给出了计算得到的压力等值线。
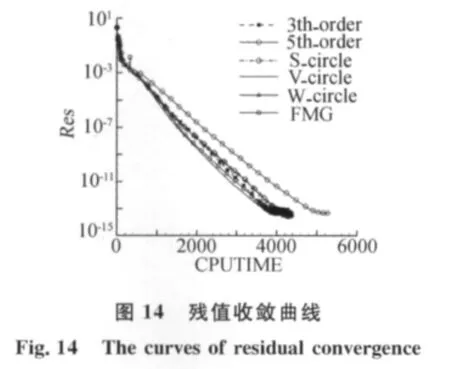
从图14残差的比较中可知,S循环、W循环、V循环和FMG的收敛速度接近于三阶格式的收敛速度,其中S循环和 W循环的收敛速度非常接近,FMG和V循环的收敛速度要稍快于三阶格式。
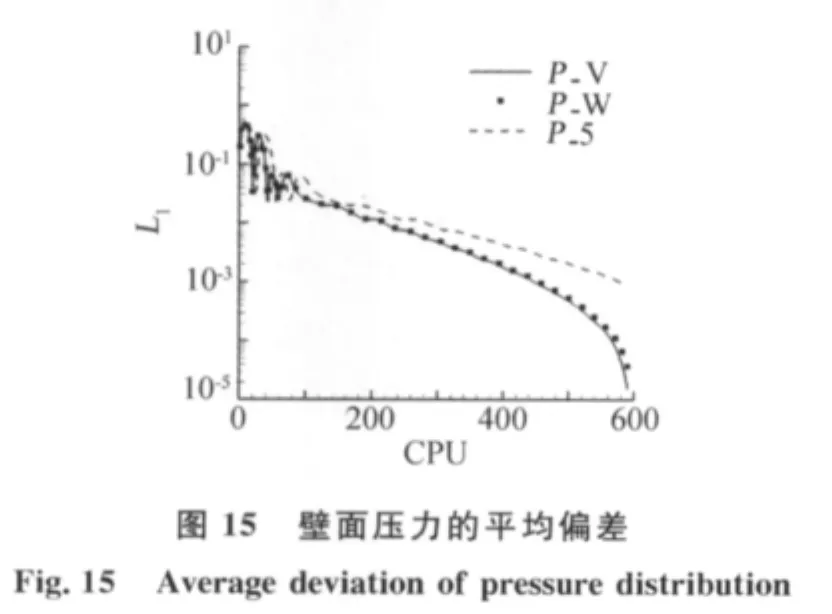
图15给出了计算过程前600s的V循环、W循环和五阶格式壁面压力的平均偏差的变化。两种pmultigrid方法均明显加快了收敛速度。


3 结束语
参考DG方法中广泛使用的p-multigrid方法的基本概念,在结合有限差分法特点的基础上,基于1阶迎风格式、3阶加权格式和5阶加权紧致格式WCNS-E-5,开展了以加快高精度格式收敛速度的pmultigrid方法研究,给出了三种基本循环(V、W、S形式)和两种组合循环(Pre_V、FMG形式)。通过典型算法的对比计算,得到以下阶段性结论:
(1)p-multigrid方法的各种循环方式,主要影响收敛历程,而最终计算结果同最高阶算法精度一致;
(2)p-multigrid方法中所采用的1阶精度算法收敛最快,5阶精度算法收敛最慢,p-multigrid方法的收敛速度整体上接近三阶精度的收敛速度,具有一定的收敛加速效果,与5阶格式相比,能够减少30%左右的CPU时间;
(3)p-multigrid方法明显的加速收敛效果主要体现在计算过程的初期,当计算结果接近收敛解时,p-multigrid方法加速收敛的效果不再明显。
在下一步研究中,将在优化p-multigrid方法循环过程和融合多重网格技术等方面开展研究工作,提高p-multigrid方法对高精度算法加速收敛的效果。
[1]MADAY Y,MUNOZ R.Spectral element multigrid,Part2:theoretical justification[R].Tech Rep.88-73,ICASE,1988.
[2]BASSI F,REBAY S.Numerical solution of the Euler equations with a multiorder discontinuous finite element method[A].Proceedings of the Second International Conference on Computational Fluid Dynamics[C],Sydney,Australia,15-19July 2002.
[3]HONG LUO,JOSEPH D.BAUM,PAINALD LÖHNER.Ap-multigrid discontinuous Galerkin method for the Euler equations on unstructured grids[J].Journalof ComputationalPhysics,2006,211:767-783.
[4]KRYSZTOF J.FIDKOWSKI,TODD A.OLIVER,JAMES LU,DAVID L.Darmofal,P-multigrid solution of highorder discontinuous Galerkin discretizations of the compressible Navier-Stokes equations[J].JournalofComputationalPhysics2005,207:92-113.
[5]KRIS VAN DEN ABEELE,TIM BROECKHOVEN,CHRIS LACOR.Dispersion and dissipation properties of the 1Dspectralvolume method and application to apmultigrid algorithm[J].J.Comp.Phys.,2007,224:616-636.
[6]ALEKSANDAR JEMCOV,JOESPH P.MARUSZEWSKI.Acceleration and stabilization of algebraic multigrid solver applied to incompressible flow problems[R].AIAA 2007-4330.
[7]XIAOGANG,DENG,HANXIN ZHANG,H.Develo-ping high-order weighted compact nonlinear schemes[J].J.Comput.Phys.,2000,165:22-44.
[8]XIAOGANG DENG.A class of high-order dissipative compact schemes[R].AIAA 96-1972,1996.
[9]刘昕,邓小刚,毛枚良.高精度非线性格式WCNS的分析研究与其应用[J].计算力学学报,2006,24(3):264-368.
[10]邓小刚,刘昕,毛枚良,等.高精度加权紧致非线性格式的研究进展[J].力学进展,2007,37(3):417-427.

