二维Woods-Burnett方程的稳定性分析
魏淑惠,包福兵,朱赠好
(1.东北石油大学 数学科学与技术学院,黑龙江 大庆 163318;2.中国计量学院 流体检测与仿真研究所,浙江 杭州 310018)
0 引 言
气体的平均分子自由程与流动特征尺度的比值定义为努森数,Kn,用来表征气体的稀薄程度。努森数越大,稀薄程度越高。飞行器重新进入大气层时,当地的平均分子自由程比较大,从而引起稀薄程度较高,这是稀薄气体动力学的传统研究方向[1-2]。近年来,微机电系统(MEMS)和纳机电系统(NEMS)迅猛发展,微/纳机电系统中流动特征尺度较小,从而使得努森数较大,流动达到滑移甚至过渡流区。微纳机电系统中的微纳尺度流动存在许多与宏观流动不一样的特性,日益受到国内外学者的关注[3-7]。但是,当稀薄程度较高时(Kn>0.1),流体应力和应变之间的线性本构关系不再成立,因此,基于线性本构关系的Navier-Stokes方程已不能够准确描述此时的流动特性,必须引入新的方法[8]。
1935年,Burnett从Boltzmann方程出发,采用Chapman-Enskog展开,获得了应力张量偏离平衡态本构关系的二阶非线性近似,得到二阶近似的Burnett方程以来,采用高阶的展流体力学方程来研究稀薄气体运动的尝试就一直没有停止。1939年,Chapman和Cowling把原始Burnett方程的随体导数用Euler方程替换,得到了常规Burnett方程。1949年,Grad[9]通过采用矩方法得到13矩方程。1991年,Zhong等人[10]为了克服常规Burnett方程的稳定性问题,通过采用线性稳定性分析的方法,在常规Burnett方程里增加了部分线性三阶项,得到增广Burnett方程。近年来,Burnett方程在稀薄气体流动方面获得了很大应用[11]。但是,关于Burnett方程能否正确描述偏离平衡态的稀薄气体流动,一直有不同意见[12]。
1993年,Woods分析常规Burnett方程[13],发现Burnett方程中的部分项不合理,经过分析推导,得到了一种修正的Burnett方程,称之为 Woods-Burnett方程。Woods-Burnett方程被认为能够较好地描述处于滑移过渡流区的气体流动和传热特性而受到很多学者的重视[13-16]。但是 Woods-Burnett方程在小扰动下不稳定[17],数值模拟过程中当网格较精细时计算就发散,这极大地限制了Woods-Burnett方程的应用。
1988年,Fiscko和Chapman发现当计算网格尺寸比气体平均分子自由程小时,扩展流体力学方程就变得不稳定[18]。这个稳定性问题早在1982年就被Bobylev发现了,通过线性稳定性分析,他指出线性化二阶Burnett方程对小于特定波长的扰动是不稳定的[19]。Balakrishnan和Agarwal[17]通过 线 性 稳 定性,发现一维Woods-Burnett方程是不稳定的。包福兵和林建忠[20]比较了 Woods-Burnett和各种类型的Burnett方程,同样发现 Woods-Burnett方程是不稳定的。并且发现,Woods-Burnett方程的临界Kn数为0.184。
本文采用线性小扰动理论,经过大量推导,在一维稳定分析的基础上,对二维常规Woods-Burnett方程进行分析,成功获得了二维Woods-Burnett方程的稳定性方程,首次得到了二维Woods-Burnett方程的稳定性曲线和临界Kn数。
1 一维常规 Woods-Burnett方程的线性稳定性分析
在笛卡尔坐标下,一维非定常可压缩粘性流动的控制方程如下:

其中,σ11是粘性应力张量xx方向的分量,q1是热通量x方向的分量,p是理想气体的压强,满足状态方程:
当考虑常规 Woods-Burnett方程时[14],粘性应力张量σ11和热通量q1的具体表达式如下:

其中ωi和θi是 Woods-Burnett方程中的系数。
遵从Bobylev的线性稳定性分析方法[19],假设扰动前气体处于稳定状态,气体的速度为零,密度和温度都为常数,可表示为:ρ=ρ0=常数,u=u0=0,T=T0=常数 。引入小扰动量:

其中,V=[ρu T]T。密度、速度、温度、位移和时间等变量按照以下形式无量纲化[19]:

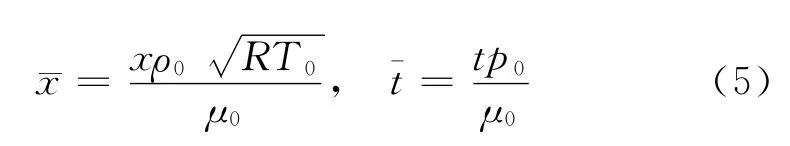
通过把扰动方程(4)代入方程(1)-(3),同时采用方程(5)形式进行无量纲化,忽略方程中小量相乘的非线性项之后,可以得到以下的无量纲控制方程(忽略了无量纲量上的上划线):

其中:
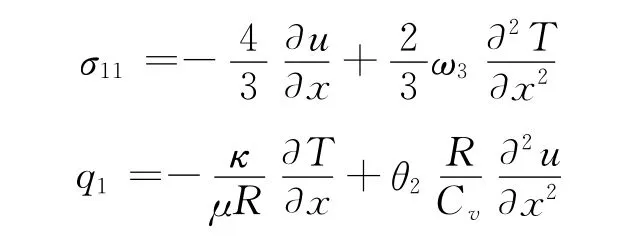
方程(6)-(8)中的扰动量可以假设成如下形式:

其中,λ=α+iβ,α和β分别代表扰动的增长系数和扩散系数,k是扰动波数,V1是扰动的振幅。
将方程(9)代入方程(6)-(8)可得如下的关于ρ1,T1和u1的齐次代数方程组:
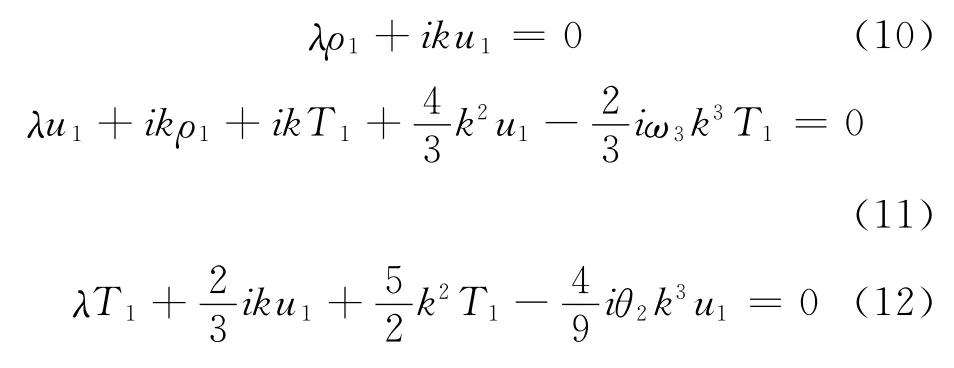
为保证这个齐次方程组存在非奇异解,必须要求这个方程的系数行列式的值为零[19],从而可以得到以下的稳定性特征方程(对于Maxwell气体):

从方程(13)可以得到λ与k的关系式。随着扰动波数k的变化,扰动的增长系数和扩散系数在复平面上的变化称为稳定性特征曲线。图1给出了一维常规Woods-Burnett方程的稳定性特征曲线。从方程(9)中λ的定义可知,当扰动增长系数α>0时,扰动振幅会随着时间的增长而变大,从而方程不稳定。从图1可以看出,随着波数k的变化,存在着正的增长系数,说明一维常规Woods-Burnett方程是不稳定的。图2给出了扰动的增长系数随波数的变化曲线。从图中可以看出,当波数大于0.907时,开始出现一个正的增长系数,说明方程开始不稳定。根据无量纲参数定义,波数与Kn数存在如下的关系:
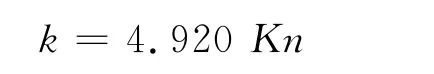
从而可以求得临界Kn数为0.184。当Knudsen数大于这个值时一维常规 Woods-Burnett方程就会发散[19]。
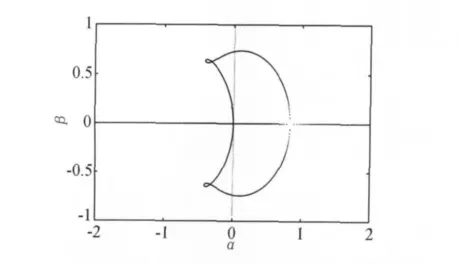
图1 一维常规Woods-Burnett方程的稳定性曲线Fig.1 Stability curve of 1-D conventional Woods-Burnett equations

图2 一维常规Woods-Burnett方程的增长系数随波数的变化Fig.2 Variations of attenuation coefficient with wave frequency for 1-D conventional Woods-Burnett equations
2 二维 Woods-Burnett方程的稳定性分析
在笛卡尔坐标下,二维非定常可压缩粘性流动的控制方程如下:


采用一维稳定性分析类似的方法,引入小扰动,代入方程无量纲化之后的二维 Woods-Burnett方程(14)-(17),并去掉非线性项之后,可以得到如下的控制方程:
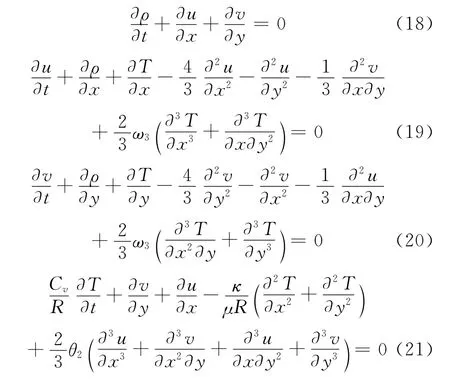
与一维分析类似,引入如下形式的小扰动:
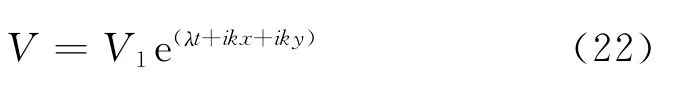
其中,V=[ρu T]T。将方程(22)形式的小扰动代入方程(18)-(21),可得关于ρ1,u1,v1和T1的齐次代数方程组,从而可以得到以下的稳定性特征方程:

根据方程(23),可以得到图3所示的二维Woods-Burnett方程的稳定性曲线。从图3可以看出,二维常规 Woods-Burnett方程的稳定性分析中,随着波数的变化,有部分增长系数大于零,这说明二维常规Woods-Burnett方程是不稳定的。图4给出了增长系数随着波数的变化曲线。从图中可以看出,当波数达到0.642时,有一个增长系数变得大于零,这说明当波数大于0.642时,方程就变得不稳定。从而说明二维常规 Woods-Burnett方程的临界波数为0.642。而根据波数与Kn数的关系,可以得到二维常规Woods-Burnett方程的临界Kn数为0.130。这个值小于一维常规 Woods-Burnett方程的临界Knudsen数为0.184。说明,二维常规 Woods-Burnett方程更加不稳定。

图3 二维常规Woods-Burnett方程的稳定性曲线Fig.3 Stability curve of 2-D conventional Woods-Burnett equations
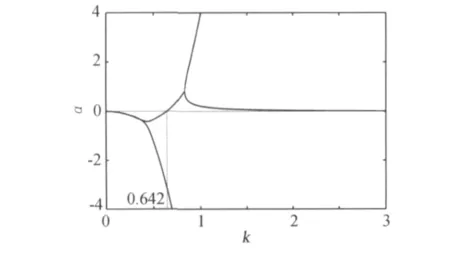
图4 二维常规Woods-Burnett方程的增长系数随波数的变化Fig.4 Variations of attenuation coefficient with wave frequency for 2-D conventional Woods-Burnett equations
3 结 论
Woods-Burnett方程是Boltzmann方程的二阶近似,能够描述轻微偏离热力学平衡时的稀薄气体流动。但是Woods-Burnett方程在小扰动下不稳定,这是限制Woods-Burnett方程广泛应用的一个重要原因。本文通过线性小扰动理论,在一维文定性分析的基础上,首次得到了二维Woods-Burnett方程的稳定性特征方程,并把稳定性方程的解表示在复平面上,得到了二维稳定性曲线.二维常规Woods-Burnett方程的临界 Knudsen数为0.130,而一维 Woods-Burnett方程的临界Knudsen数为0.184,这说明二维Woods-Burnett方程比一维 Woods-Burnett方程更加不稳定。
二维稳定性的发现对进一步研究 Woods-Burnett方程具有重要意义,使得我们能够确定二维Woods-Burnett方程在什么情况下会变得不稳定,二维Woods-Burnett方程能够应用于哪些范围内的流场。如何增加 Woods-Burnett方程的稳定性以及把各类Burnett方程应用到各种处于稍微偏离平衡态的连续流或近连续滑移流动中是今后研究的重点。
[1]沈青.稀薄气体动力学[M].北京:国防工业出版社,2003.
[2]李志辉,张涵信.稀薄流到连续流的气体运动论统一算法研究[J].空气动力学学报,2003,21(3):255-266.
[3]林建忠,包福兵,王瑞金,等.微纳流动理论及应用[M].北京:科学出版社,2010.
[4]GAD-EL-HAK M.Review:flow physics in MEMS[J].Mecan Indust,2001,2:313-341.
[5]KARNIADAKIS G,BESKOK A,ALURU N.Microflows and Nanoflows,fundamentals and Simulation[M]:Springer,2005.
[6]秦丰华,孙德军,尹博远.长微管道气体流动的近似解析解[J].空气动力学学报,2002,20(1):49-56.
[7]沈青,蒋建政.有限长度的过渡领域微槽道流动——分析预测和试验的比较[J].空气动力学学报,2008,26(2):257-262.
[8]HO C M,TAI Y C.Micro-Electro-Mechanical-Systems(MEMS)and fluid Flows[J].Annu.Rev.Fluid Mech.,1998,30:579-612.
[9]GRAD H.On the kinetic theory of rarefied gases[J].Commun.Pure Appl.Math.,1949,2:331-407.
[10]ZHONG X L,MACCORMACK R W,CHAPMAN D R.Stabilization of the Burnett equations and application to hypersonic flows[J].AIAA J.,1993,31(6):1036-1043.
[11]AGARWAL R K,YUN K Y,BALAKRISHNAN R.Beyond Navier-Stokes:Burnett equations for flows in the continuum-transition regime[J].Phys.Fluids,2001,13(10):3061-3085.
[12]COMEAUX K A,CHAPMAN D R,MACCORMACK R W.An analysis of the Burnett equations based in the second law of thermodynamics[R].AIAA,1995,95-0415.
[13]WOODS L C.An Introduction to the Kinetic Theory of Gases and Magnetoplasmas[M],Oxford:Oxford University Press,1993.
[14]REESE J M,WOODS L C,THIVET F J P,et al.A second-order description of shock structure[J].J.Comput Phys.,1995,117(2):240-250.
[15]REESE J M,GALLIS M A,LOCKERBY D A.New directions in fluid dynamics:non-equilibrium aerodynamic and microsystem flows[J].Philos.T.Roy.Soc.A.,2003,361(1813):2967-2988.
[16]LOCKERBY D A,REESE J M,GALLIS M A.The usefulness of higher-order constitutive relations for describing the Knudsen layer[J].Phys.Fluids,2005,17(10):100609-1-6.
[17]BALAKRISHNAN R,AGARWAL R K.A comparative study of several higher-order kinetic formulations beyond Navier-Stokes for computing the shock structure[A].In 37th AIAA Aerospace Sciences Meeting and Exhibit[C],1999.Reno,NV.
[18]FISCKO K A,CHAPMAN D R.Comparison of Bur-nett,super-Burnett and Monte Carlo solutions for hypersonic shock structure[A].in Proceedings of the 16th International Symposium on Rarefied Gas Dynamics[C],1988.
[19]BOBYLEV A V.The Chapman-Enskog and Grad methods for solving the boltzmann equation[J].Soviet Physics,1982,27(1):29-31.
[20]BAO F B,LIN J Z.Linear stability analysis for various forms of one-dimensional Burnett equations[J].Int.J.Nonlinear Sci.,2005,6(3):295-303.

