高阶精度格式WCNS在三角翼大攻角模拟中的应用研究
王光学,邓小刚,刘化勇,王运涛
(中国空气动力研究与发展中心 空气动力学国家重点实验室,四川 绵阳621000)
0 引 言
高阶精度格式作为数值计算的重要工具一直在诸多学科领域占有显要地位,譬如,湍流的直接数值模拟(DNS)和大涡模拟 (LES)、计算气动声学(CAA)、计算电磁学(CEM)和磁流体力学(MHD)等。通过高阶精度数值计算,一方面可以观察流动细节、为机理分析提供精细数据;另一方面可以弥补实验条件限制和理论分析的不足,扩大研究范围。特别是,随着人们对计算精度要求的不断提高,在工程应用领域和研究领域都越来越需要更为细致准确的数值模拟,这为高阶精度格式的研究和应用创造了新的契机。
WCNS是邓小刚自20世纪90年代提出的高阶精度格式。首先,他们通过在中心型紧致格式中加入耗散项,于1996年构造了单参数线性耗散紧致格式(Dissipative Compact Schemes,DCS)[1],通过调整单一参数,精度可分别达到3至9阶。同时,他们又提出了自适应插值的概念,构造了一类高阶紧致非线性格式(Compact Nonlinear Schemes,CNS)[2],这样可以解决DCS因为线性格式很难用于含有激波流场的困难。然后通过引入加权思想,构造了一系列加权紧致非线性格式 WCNS(Weighted Compact Nonlinear Scheme)[3-5],包括隐式和显式两种类型。
50年代以来,对三角翼大攻角绕流的研究一直是流体力学工作者们所特别关注的一个重要方向。在这个典型的流场环境中,包含了非常丰富和复杂的流体力学现象。这些现象的研究与探讨对空气动力学理论的发展与完善具有重大意义,对提高现代飞行器性能具有重要价值。随着计算机技术和高精度、非线性计算方法的迅速发展,开展了广泛的数值模拟和理论研究,但由于该现象的高度复杂性,人们对其流动机理尚未充分掌握,还不能形成一个完整合理的理论以解释涡破裂现象的产生和发展过程。
本文通过求解任意坐标系下的雷诺平均的N-S方程,采用5阶精度的加权紧致非线性格式(WCNSE-5)和多块对接结构网格技术,在与相应试验结果对比的基础上,详细研究了 WCNS-E-5格式以及两种湍流模型对主涡二次涡相互作用、涡破裂位置和表面压力分布的影响。本文的研究结果表明,高阶精度格式WCNS能成功应用于三角翼的跨声速大攻角流动,网格规模的增加进一步提高流场分辨率,SST湍流模型相对SA湍流模型在三角翼大攻角流动中具有更好的适用性。
1 计算构型和计算方法
本文采用的计算模型是65°后掠三角翼,它是1996年NASA Langley为研究该外形的雷诺数、马赫数影响而完成的试验模型,包括可替换的四个前缘外形,本文选用的是尖前缘,其前缘半径为0。风洞试验主要是在NASA Langley的NTF跨声速风洞中完成的,包括测力和测压试验。后来该外形成为国际旋涡试验研究的标准模型,在德国的DLR等研究机构完成了PSP、PIV试验。计算构型如图1所示,模型详细介绍见文献[6]。
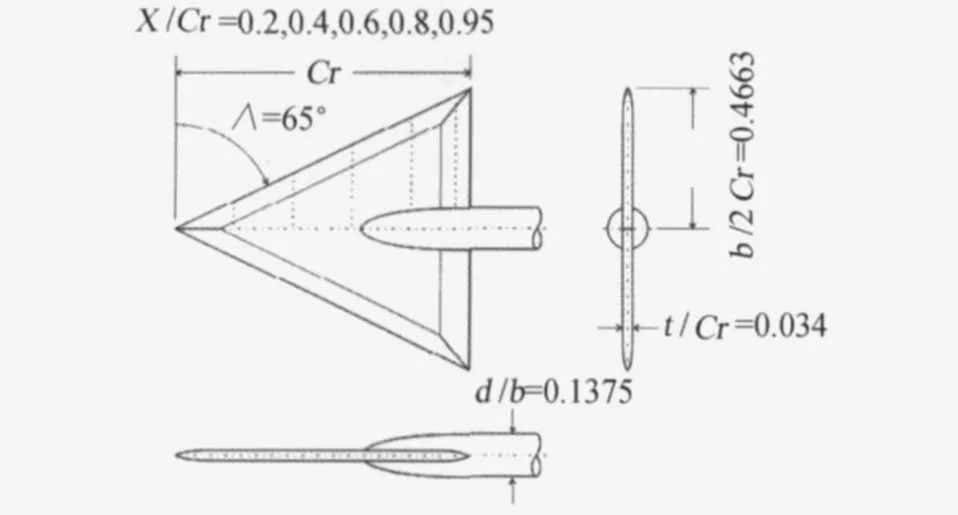
图1 65°后掠三角翼构型Fig.1 Configuration of the 65°delta wing
本文模拟的状态为:与测力测压试验[6]对应的状态为马赫数 M=0.85,攻角α=-1°~27°,雷诺数Re=6×106;与PSP[6]、PIV[8]试验对应的状态为马赫数M=0.8,攻角α=25.5°,雷诺数Re=2×106。力矩参考点距头部顶点三分之二根弦长。Cp分布为沿流向5个截面,其中X/Cr=0.2、0.4、0.6、0.8、0.95。
本文采用的计算方法为:对流项离散格式采用5阶精度加权紧致非线性格式(WCNS-E-5),粘性项离散格式为4阶精度中心格式,湍流模型采用了SA一方程和SST两方程模型,计算中采用了并行技术加速。
其中5阶精度加权紧致非线性格式(WCNS-E-5)对流项离散格式如下:(a)内点格式
对流项离散采用原始变量型的 WCNS-E-5格式,设网格间距为h,以ξ方向为例
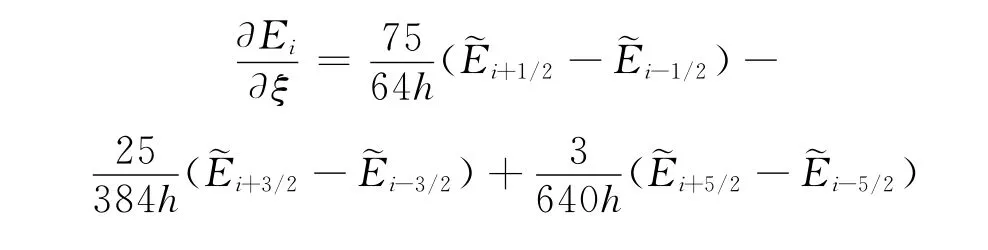
(b)边界格式
边界和靠近边界格式如下
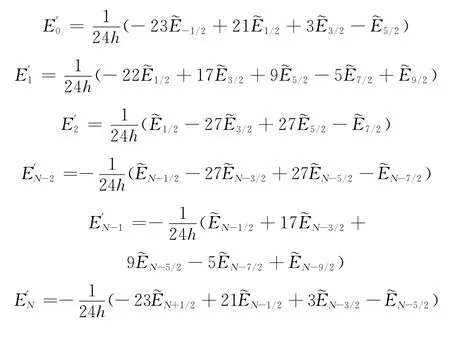
2 网格影响分析
本文采用的计算网格均自主生成,网格结构为多块对接网格(1-to-1),网格分为粗网格、中等网格和细网格三种,网格的详细信息如表1所示,图2给出了粗网格的表面网格和对称面网格。由表中可以看出,在该网格序列中,各套网格之间并没有2倍数关系,这也许会给网格收敛性研究带来一定的影响。
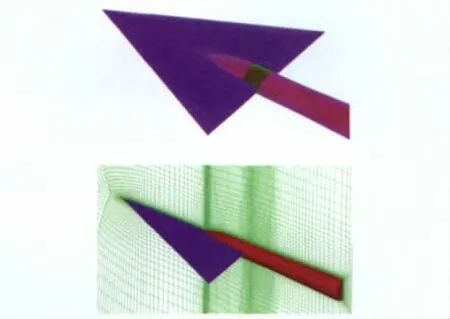
图2 三角翼的计算网格Fig.2 Computational grid of the 65°delta wing
表1 网格统计列表Table 1 Computational grid size for the case
三套网格的网格拓扑关系相同,以“C”型网格为主导,计算区域的远场边界取为25倍弦长。壁面的第一排网格达到了1.0×10-6弦长,网格在背风区和各个剪切层附近均进行了适当的加密,以保证分离区、附面层内和剪切层的数值模拟精度。
首先回顾尖前缘后掠翼的前缘分离的基本特性,由于是尖前缘,在较小的攻角主涡分离就开始于翼尖,从下至上流动卷起形成主涡分离,攻角增大,主涡直径和强度均增加,位置向机翼内侧移动。主涡旋转产生展向流动,在旋涡下部、三角翼的上翼面加速,出现负压力峰值,该点沿展向到翼边缘是逆压梯度,将诱导边界层分离,产生二次分离和二次旋涡,在主涡负压力峰值外侧又出现二次负压力峰值。当攻角大到一定程度,主涡开始破裂,当破裂位置发展到机翼表面,将引起突然失速。
图3是马赫数M=0.85,攻角α=20.6°,雷诺数Re=6×106状态下,不同计算网格的不同流向位置横截面压力系数的比较。
在X/Cr=0.2截面,中、细网格的上翼面出现了两次负压力系数峰值,表明在此截面,三角翼上翼面流动出现了主涡和二次涡,而粗网格的二次涡不明显出现。随网格加密,计算的压力系数曲线与试验结果更为接近,并且更明显分辨出主涡和二次涡。从X/Cr=0.4、0.6、0.8截面看出,中、细网格的计算结果比较接近。
图4是粗、细网格的X/Cr=0.2截面的压力云图和速度矢量图。粗网格分辨率较低,其二次涡不明显,而细密度网格对流场的描述更细致,计算结果与试验结果更为接近,本文下面的计算都采用细网格模拟。
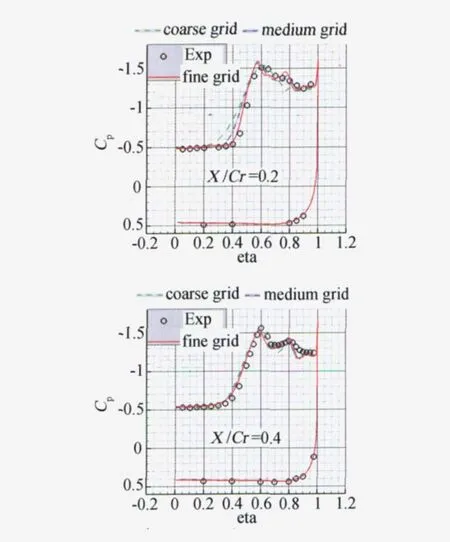
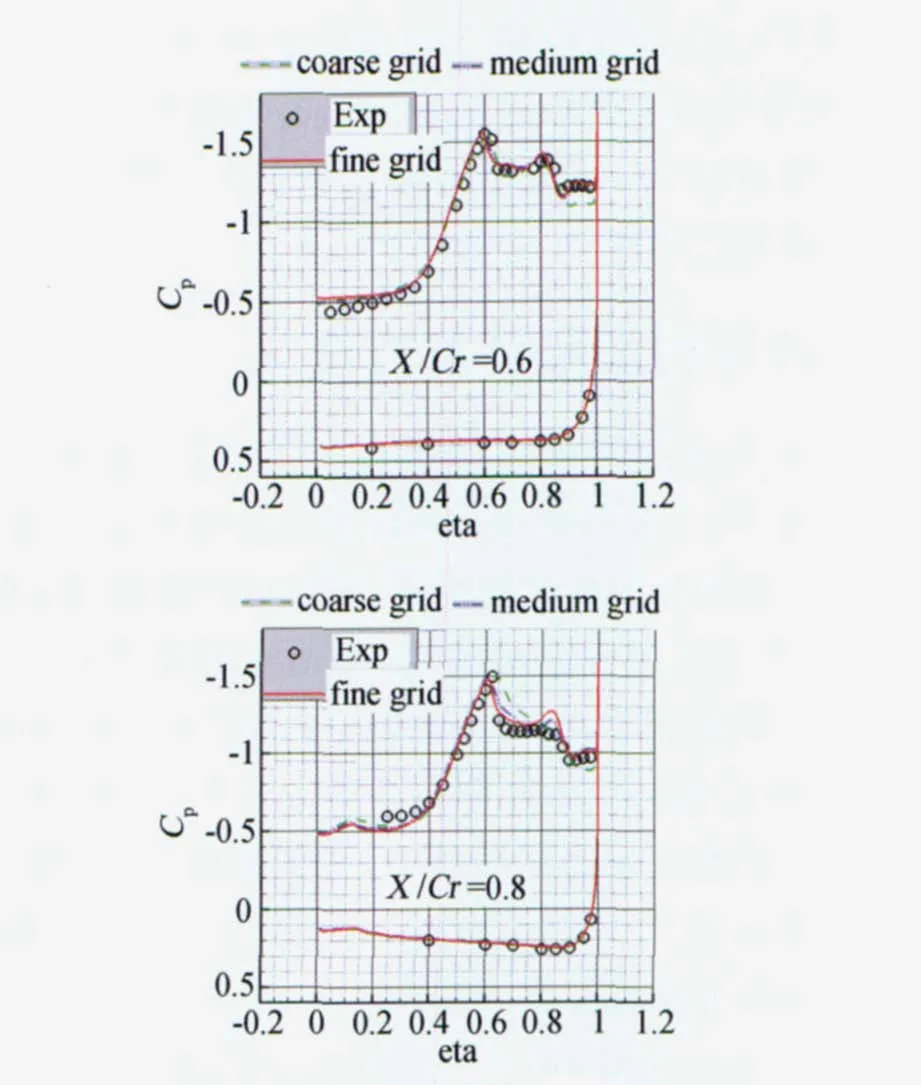
图3 不同计算网格的截面压力系数的比较Fig.3 Comparison of surface pressures coefficient forα=20.6°
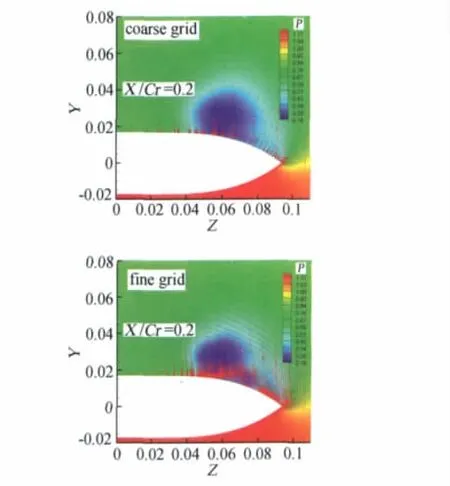
图4 X/Cr=0.2截面的压力云图和速度矢量图Fig.4 Comparison of pressures and velocity distribution at X/Cr=0.2
虽然随网格规模的增加,提高了流场分辨率,中、细网格的计算结果也比较接近了,但依然不能称其为达到网格收敛性。在高阶精度模拟条件下,网格收敛性研究对网格序列的要求以及判断依据有待进一步研究。
3 湍流模型影响分析
在流场求解的RANS方法中,NS方程求解采用了高阶精度,约束计算精准度的瓶颈之一便是湍流模型了,而不同湍流模型在不同流场特性中又表现不同,为了考核高阶精度求解条件下,湍流模型在三角翼大攻角旋涡流动中的表现,本节选取了一方程SA湍流模型和两方程SST湍流模型进行对比计算。
图5是本文细网格计算结果与文献[6]试验结果的比较。在攻角20°之前,两种湍流模型的法向力系数计算结果与试验结果都相近;在大攻角范围,SST湍流模型的法向力系数随攻角变化的拐折点与试验结果一致,都在攻角23.6°和24.6°,其中攻角24.6°时主涡破裂,SA湍流模型的计算结果在本文计算的攻角范围内没出现拐折,表明主涡没有破裂。俯仰力矩系数的计算结果与实验结果还有一定差距,特别是俯仰力矩系数曲线斜率和在大攻角时的曲线拐折点的模拟差距较大,这是数值模拟的难点也是进一步研究的重点。
图6是两种湍流模型在攻角20.6°时三角翼上表面压力系数等值线云图的比较。右图是采用SST湍流模型计算的结果,在三角翼的一侧可以仔细分辨出两道绿色条纹,从顶部向尾部延伸,说明出现了主涡、二次涡分离;左图是采用SA湍流模型计算的结果,其SA绿色条纹仅一道,表明只有主涡分离,二次涡不明显。这从图7两种湍流模型的截面压力系数的比较也可看出,SST湍流模型的计算结果与试验更为接近,沿展向出现了两次压力峰值,表明出现了主涡和二次涡,其位置也和试验一致,而SA湍流模型的计算结果没有出现两次压力峰值。
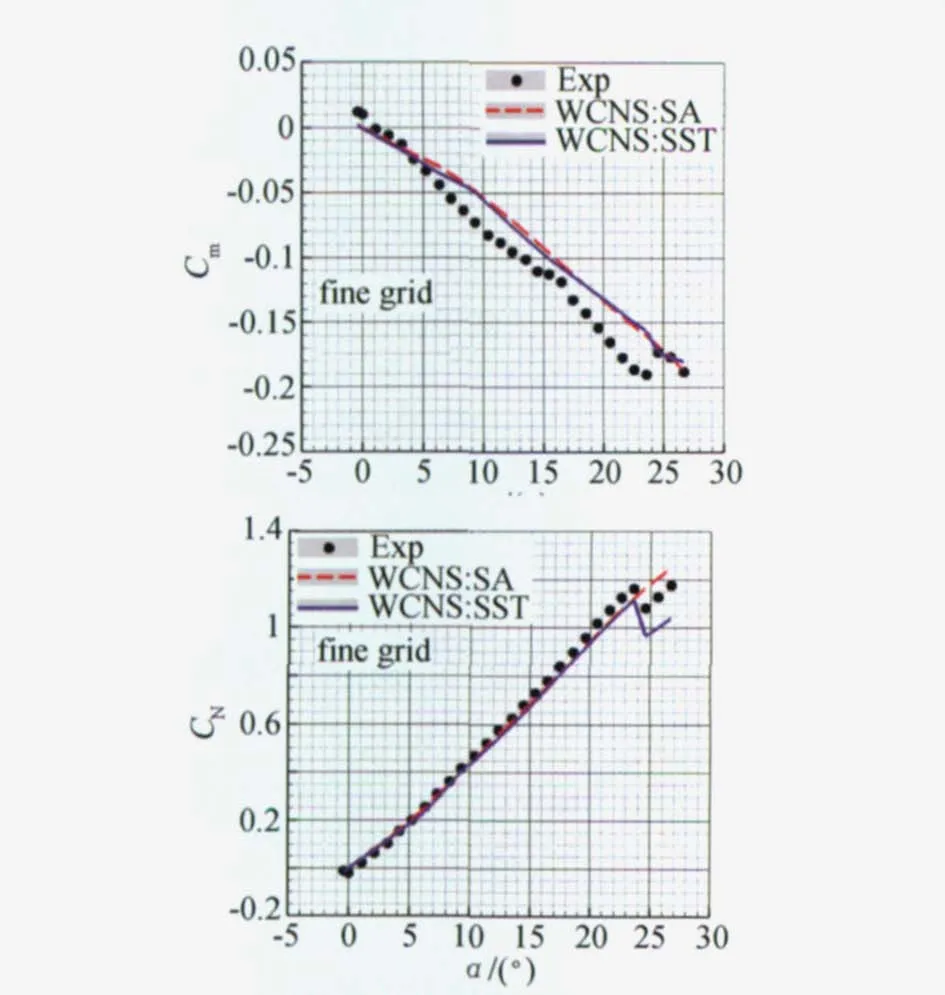
图5 气动力系数的比较Fig.5 Comparison of aerodynamics coefficient
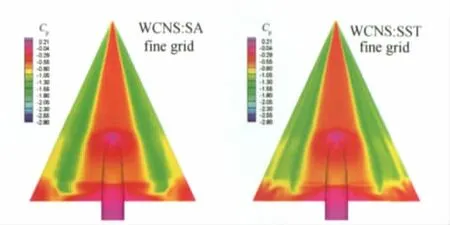
图6 表面压力系数的比较(SA、SST湍流模型)Fig.6 Comparison of surface pressures distributions
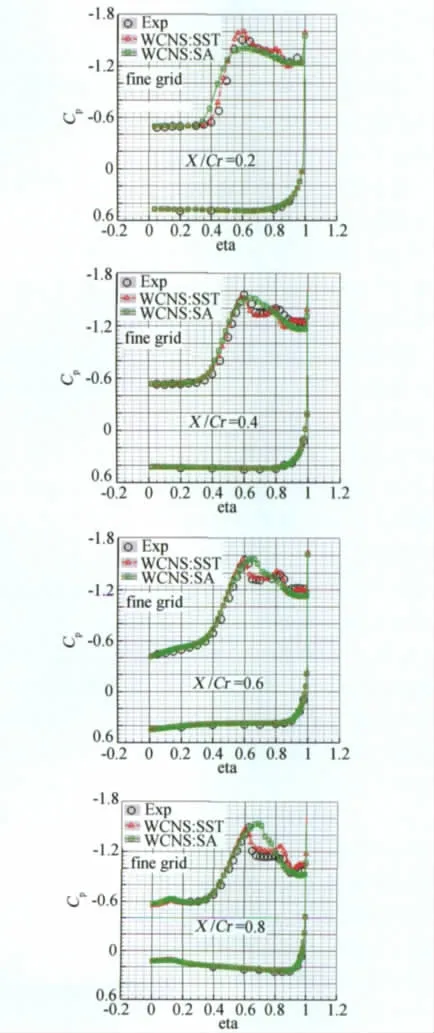
图7 截面压力系数的比较(SA、SST湍流模型)Fig.7 Comparison of pressures coefficient
通过以上分析说明,在本文采用的计算方法中,SST湍流模型在模拟大攻角大分离流动时比SA湍流模型更为适用。
4 涡破裂位置的计算结果与分析
本节采用细网格和SST湍流模型精细模拟了马赫数0.8、攻角25°,雷诺数200万状态下的三角翼绕流。对于这个状态,涡破裂位置是数值模拟的难点和重点,并且在三角翼上表面出现了超音速区域,以及横向流动产生较强激波,这都对高阶精度格式数值模拟提出了挑战。
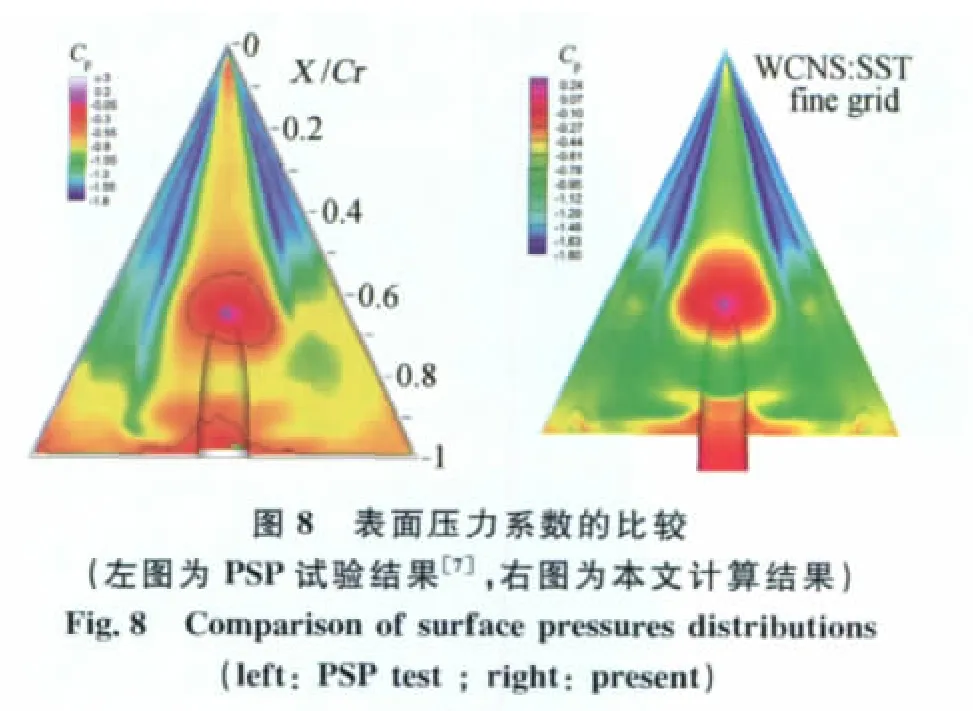
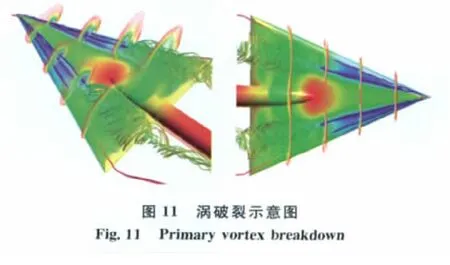
图8是该状态下的表面压力系数的比较,其中左图为文献[7]的PSP试验结果,左侧表面不是太光滑,出现左右不对称。右图为本文计算结果。其计算结果与实验结果右侧比较,主涡、二次涡的位置和主涡破裂位置都吻合较好。图9、10是X/Cr=0.6、0.7截面的速度矢量图,其中左图为文献[8]的PIV试验结果,右图为本文计算结果。图11主涡破裂位置示意图,以及X/Cr=0.2、0.4、0.6、0.8截面的压力等值线图。从这些图中看出,在该计算状态下,主涡、二次涡从三角翼顶端分离出,主涡涡核位置较高,其旋转产生侧向流动,在涡核下面沿展向是逆压梯度,与附面层作用,导致附面层分离,产生二次涡;在X/Cr=0.6截面,主涡还没出现破裂,从截面速度矢量图中看出主涡逆时针旋转,涡核清晰;在X/Cr=0.7截面,主涡破裂,在涡核位置出现反向旋转流动,从涡破裂示意图看出,在X/Cr=0.7截面附近沿涡核流线不再紧密聚集,流线从涡核起向外旋转散开,涡结构已经变得很松散,而二次涡并没有因为主涡破裂而消失或破裂。
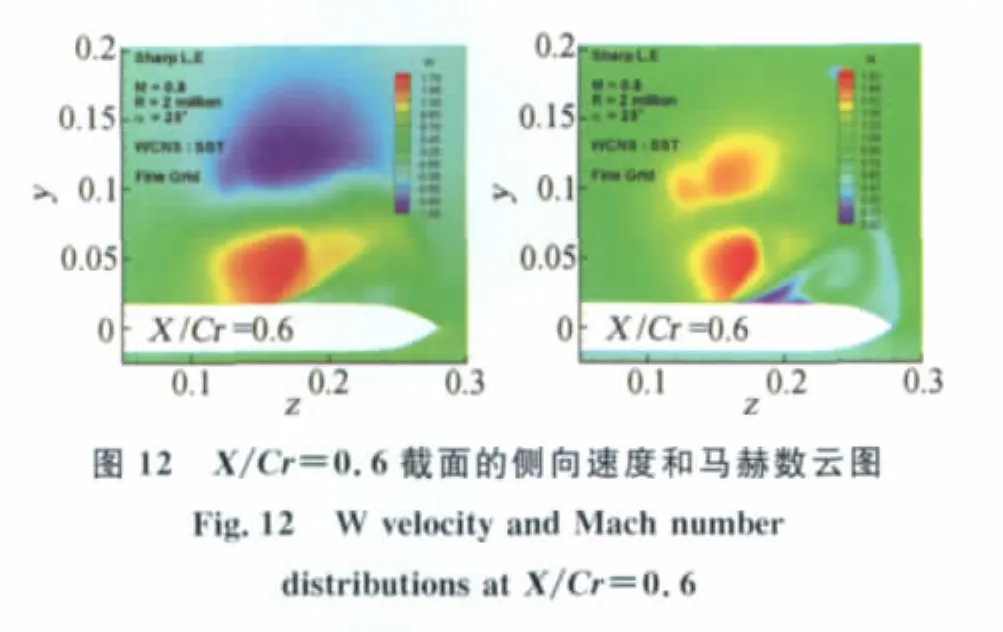
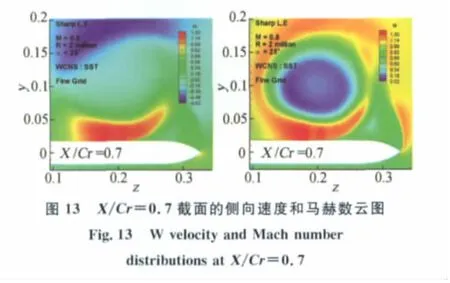
同时,从图12、13的X/Cr=0.6、0.7截面的侧向速度和马赫数云图中看出,由于本文选取的计算状态为跨声速流动,其三角翼上表面出现了超音速区域,在主涡下部靠近壁面位置,激波诱导附面层分离,产生二次分离。对于求解含有激波的跨/超音速流动时,对计算格式的要求更加苛刻,不仅要求格式能以极小的数值耗散来体现小尺度的流场结构,还希望它具有光滑捕捉流场间断的性能。而本文采用的高阶精度格式(WCNS)在这方面具有一定优势,在减小数值耗散的同时,能光滑捕捉激波,较好地解决了这两个几乎矛盾的双重目标。


5 结 论
本文采用5阶精度的加权紧致非线性格式(WCNS-E-5)和多块对接结构网格技术,通过求解任意坐标系下的RANS方程,数值模拟了65°后掠三角翼的复杂流场,主要研究了 WCNS-E-5格式以及两种湍流模型对主涡二次涡相互作用、涡破裂位置和表面压力分布的影响。通过与相应的试验结果相比较,得到以下一些基本结论:
(1)高阶精度格式(WCNS-E-5)能成功应用于三角翼的跨声速大攻角流动。
(2)SST湍流模型相对SA湍流模型在三角翼大攻角流动中具有更好的适用性。
(3)随网格规模的增加,提高了数值模拟精度和流场分辨率,但高阶精度数值模拟条件下的网格收敛性有待进一步研究。
(4)本文采用的数值方法能较准确地模拟三角翼主涡破裂位置,其结果与PSP、PIV实验结果一致。
[1]DENG X G,MAEKAWA H,SHEN C.A class of high order dissipative compact schemes[R].AIAA Paper 96-1972.
[2]DENG X G,MAEKAWA H.Compact high-order accurate nonlinear schemes[J].J.Comput.Phys.,1997,130:77-91.
[3]DENG X G,MAO M L.Weighted compact high-order nonlinear schemes for the Euler equations[R].AIAA Paper 97-1941.
[4]DENG X G,ZHANG H X.Developing high-order weighted compact nonlinear schemes[J].J.Comput.Phys.,2000,165:24-44.
[5]DENG X.High-order accurate dissipative weighted compact nonlinear schemes[J].ScienceinChina(SeriesA),2002,45(3):356-370.
[6]CHU J,LUCKRING J M.Experimental surface pressure data obtained on 65°delta wing across Reynolds number and mach number ranges[R].NASA TM 4645,1996.
[7]KONRATH R,KLEIN C,ENGLER R H,et al.Analysis of PSP results obtained for the VFE-2 65°delta wing configuration at subsonic and transonic speed[R].AIAA Paper 2006-0060,2006.
[8]SCHRÖDER A,AGOCS J,FRAHNERT H,et al.Application of stereo-PIV to the VFE-2 65°delta wing configuration at sub-and transonic speeds[R].AIAA Paper 2006-3486,2006.

