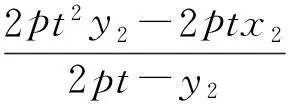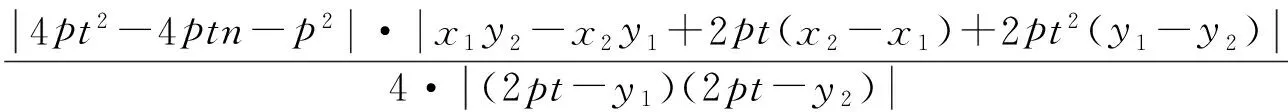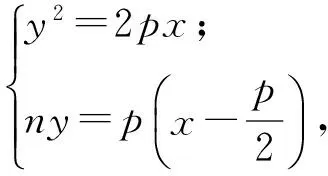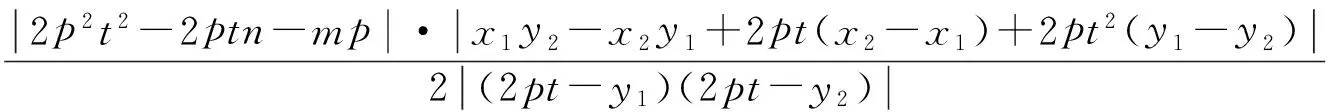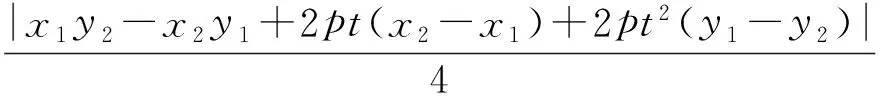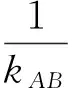对2012年江西省数学高考理科第20题的研究

●

(彭阳县第三中学 宁夏彭阳 756500)

对2012年江西省数学高考理科第20题的研究

●王伯龙

(彭阳县第三中学 宁夏彭阳 756500)

例1已知3个点O(0，0)，A(-2，1)，B(2，1)，曲线C上任意一点M(x,y)满足

(1)求曲线C的方程.

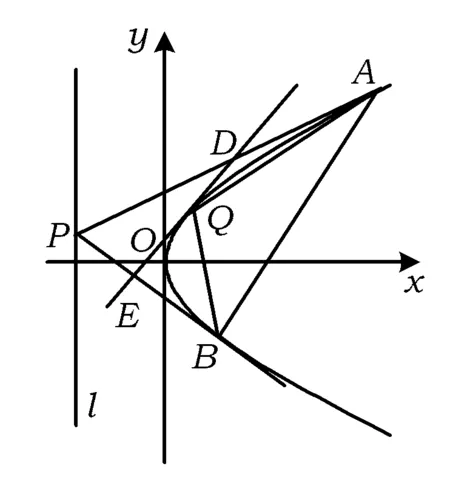
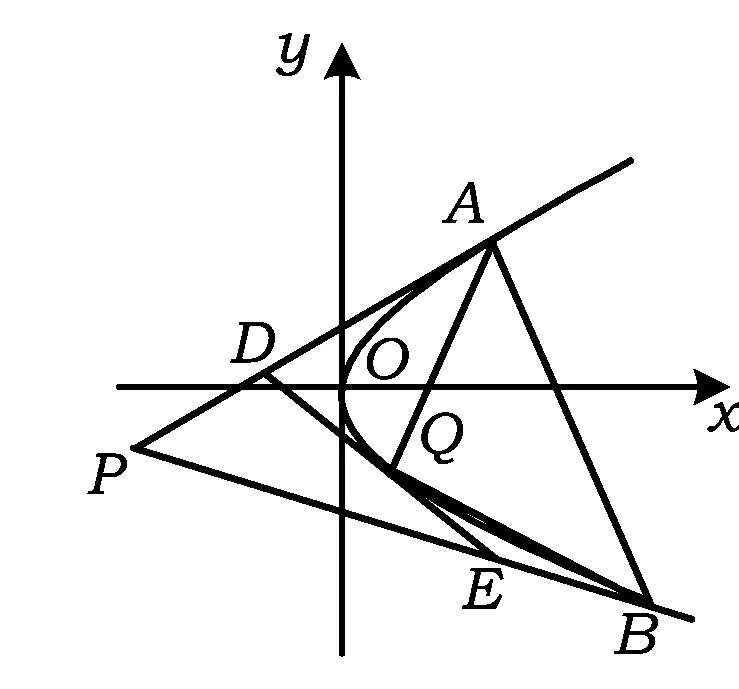
(2)动点Q(x0,y0)(-2

(2012年江西省数学高考理科试题)

本题综合的考查了圆锥曲线上的动点、切线及其三角形面积等相关知识.当笔者看到该题后的第一感觉是第(2)小题在设置上立意新颖，独具匠心，凝聚了命题专家的灵感与智慧，值得继续学习与研究.

易得曲线C的方程为：x2=4y.对于第(2)小题，探究的结果是存在定点P(0,-1)，使得△QAB与△PDE的面积之比是常数2.仔细分析题中的条件和得出的结论，不难发现：点P(0,-1)恰是抛物线C的准线y=-1与对称轴的交点，已知点A与点B的连线过抛物线的焦点(0,1)，容易验证PA，PB恰是抛物线的2条切线，因而第(2)小题得到的结论是特殊的情形，一般化可得：

图1

又DE:2pty=p(x+2pt2)，即

DE:2ty=x+2pt2.

(1)

(2)

(3)

(4)

将式(1)，式(2)代入式(4)化简得

(5)

y2-2ny-p2=0，

由根与系数的关系得

y1+y2=2n,y1y2=-p2.

因此

(2pt-y1)(2pt-y2)=4p2t2-2pt(y1+y2)+y1y2=4p2t2-4ptn-p2，

将其代入式(5)化简得

(6)

由式(3)和式(6)得

将结论1中“过准线l上任意一点”推广为“过定直线l:x=-m(m>0)上任意一点”，结论是否成立？经过尝试，便有如下的结论.

证明如图1，设动点Q(2pt2,2pt)，P(-m,n)，A(x1,y1)，B(x2,y2),则切点弦

PA：y1y=p(x+x1)，PB:y2y=p(x+x2),AB:ny=p(x-m).

又DE:2pty=p(x+2pt2)，即

DE:2ty=x+2pt2.

(7)

将式(1)，式(2)代入式(7)化简得

(8)

y2-2ny-2pm=0,

又由根与系数的关系得

y1+y2=2n,y1y2=-2pm.

因此

(2pt-y1)(2pt-y2)=4p2t2-2pt(y1+y2)+y1y2=4p2t2-4ptn-2pm,

将其代入式(8)化简得

(9)

由式(3)和式(9)得

将结论中的“过定直线l:x=-m(m>0)上任意一点”，换成“过抛物线外的任意一点P(s,q)”，结论是否成立？

图2

结论3的证明,可仿结论2的证法，有兴趣的读者可自行证明.笔者经过演算，上述结论是抛物线特有的性质，对于椭圆、双曲线不成立.

上述结论体现了抛物线切点三角形的面积和外切三角形面积之间的一个定比关系，如果从斜率的角度出发去研究也会得到有趣的结论.关于这方面的研究文献[1]已给出相应的结论.

定理[1]过抛物线C:y2=2px(p>0)外任意一点P作抛物线的2条切线PA,PB,切点分别为A,B,动点Q为抛物线C上在A,B之间部分上的任意一点，抛物线C在点Q处的切线分别交PA,PB于点D,E(如图2).用kAB,kBQ,kQA分别表示直线AB,BQ,QA的斜率，用kA,kB,kQ分别表示抛物线上切于点A,B,Q处的切线的斜率，则

[1] 苗相军，孙胜田.圆锥曲线外切三角形和切点三角形边的斜之关系[J].数学通讯，2012(5)：48-49.