四法并举 彰显活力——2012年浙江省数学高考理科第17题赏析

●

(鲁迅中学 浙江绍兴 312000)

四法并举彰显活力
——2012年浙江省数学高考理科第17题赏析

●陆立峰

(鲁迅中学 浙江绍兴 312000)

2012年浙江省数学高考试题依然秉承了“起点低、坡度缓、层次多、区分好”的鲜明特色，其中又不乏一些适度创新、题小意深的经典之作.本文就以理科第17题为例进行解法探求和赏析.

例1设a∈R，若x>0时均有[(a-1)x-1](x2-ax-1)≥0，则a=________.

(2012年浙江省数学高考理科试题)

1 解法探索

解法1根轴法

由题意分析可得a>1，则原不等式可转化为

其中x1,x2是方程x2-ax-1=0一正一负的2个根.不妨设x1<0,x2>0，由三次不等式穿根法可知，要使得对一切x>0时均有

[(a-1)x-1](x2-ax-1)≥0

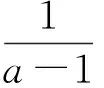
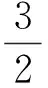
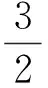
点评根轴法是简单高次不等式中的基本方法.由题意对一切x>0不等式均成立，说明正根x2为重根，此法解题也是水到渠成的事情.

解法2数形结合

本题按照一般思路，则可分为以下2种情况

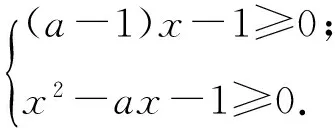
受经验的影响，很多学生认为本题可能是错题或者解不出本题.其实在x>0的整个区间上，可将其分成2个区间，在各自的区间内恒正或恒负,如图1所示.

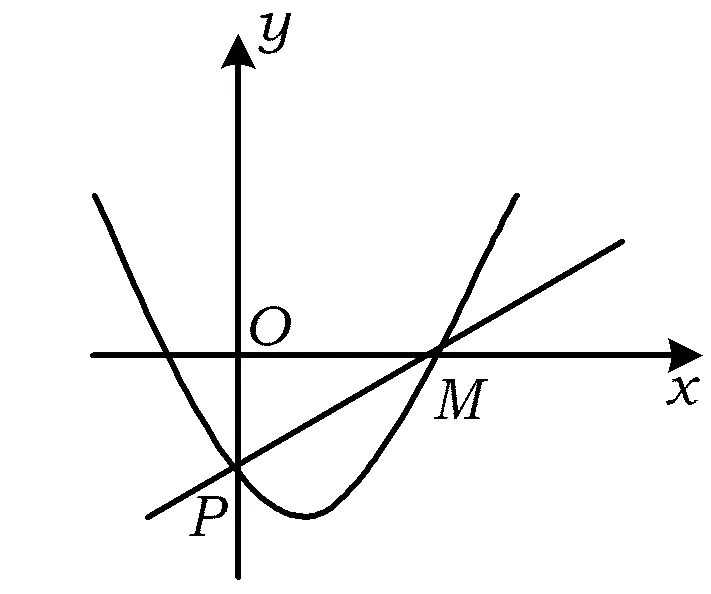
图1

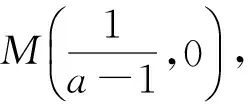
解得

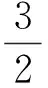
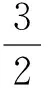
解法3变换主元

把a看作主元，则原不等式可化为

(xa-x-1)(-xa+x2-1)≥0，

进一步可整理为

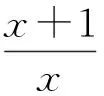
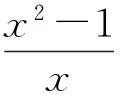
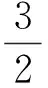
即

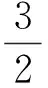
当x=2时，原不等式化为

因此

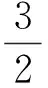
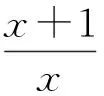
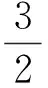
即

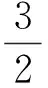
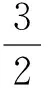
点评变换主元，看成关于a的二次不等式是个大胆的想法，此想法能否实现需要扎实的基本功.经过转换后就变成含参不等式的解法，过程有点繁琐，属于小题大做.但在解题过程中，往往会得到下面的简便方法.

解法4特殊法

把a看作主元，则原不等式可化为

(xa-x-1)(-xa+x2-1)≥0，

进一步可整理为

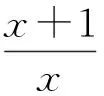
故

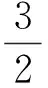
点评解法4一时难以捕捉，但在分析解答过程和求解的结果来看，这是神来之笔，是在深刻理解知识基础上的灵机一动，并且这种方法揭示了特殊性存在于一般性之中的哲学思想.

2 试题赏析

本题简洁朴素，但具有高考试题概念的深刻性、思辨的逻辑性、解法的多样性等特点，是整份试卷中的一大亮点.题目虽小，但题精意蕴，细细品味，对今后的复习备考具有很多有益的启示.

2.1 突出本质显导向

考试说明指出，数学学科的考试，按照“考查基础知识的同时，注重考查能力”的原则，确立以能力立意命题的指导思想，将知识、能力和素质融为一体，全面检测考生的数学素养.要发挥数学作为主要基础学科的作用，既考查考生的基础知识、基本技能的掌握程度，又考查对数学思想方法、数学本质的理解水平以及进入高等学校继续学习的潜能.本题以不等式为载体，既考查基础知识，又考查数形结合等基本思想方法，还体现特殊性与一般性的哲学思想.在课堂教学过程中，教师除了传授知识本身以外，还应该教给学生哪些东西？学生高中毕业十年、二十年之后依然留在脑海中的这些东西，才是数学最本质、最核心的思想方法，也是数学教学的目的.此题还传递出一个信息，高中数学教学依靠“题型+技巧+大运动量训练”的教学难以适应高考，呼唤突出数学本质、实现高中数学教学自然回归，有利于新课程改革的落实.

2.2 总结反思探题源

一道好的试题，并不一定都是新题，因此命题者无需有意回避教材或资料中的常见试题，而恰是这些题目反而成为命制试题的来源.在不等式恒成立上设置考题，知识背景公平，很好的体现考查基础知识的命题要求，符合中学教学实际及考试说明的要求.此题在平时上含参不等式这块内容时是作为2个独立的小题来求解的,即：

(1)设a∈R，若x>0时均有(a-1)x-1≥0，求a的取值范围；

(2)设a∈R，若x>0时均有x2-ax-1≥0，求a的取值范围.

在这里把2个小题合在一起可谓独具匠心，使人倍感亲切，并给人似曾相识的感觉，不会作为压轴题而使考生望而生畏.其实2011年浙江省数学高考理科试题的第10题，讨论方程

g(x)=(ax+1)(cx2+bx+1)=0

根的个数是否也有异曲同工之妙呢？

2.3 能力立意促选拔

选拔性是高考试题最核心的一个功能，本题虽然是一道很普通的填空题，内容上似曾相识，但在形式上还是推陈出新的.本题看似平淡，但已经将基础知识、方法、能力和数学素养的考查融为一体.使每一位考生的能力尽显出来，使高考的选拔功能得以实现.本题之所以能很好地体现选拔性的要求，首先是解题入口宽，既可以用代数方法计算，也可数形结合等常用方法求解；其次是区分度较好，因为着眼点不同，解题的方式方法不同，每种方法各有千秋，效果自然也就大不相同，能够为高校选拔相应的优秀人才.

高考试题是命题组教师集体智慧的结晶，是平时学生学习和教师教学过程中的宝贵财富.如何充分利用这些题源，开展一题多解和多题一解，也是教师日常教学中的一件非常有意义的事.