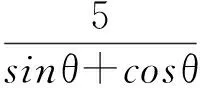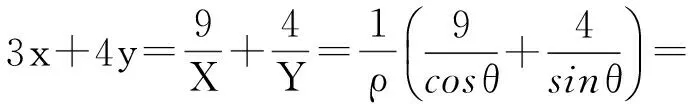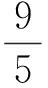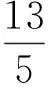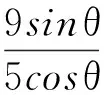一道浙江省数学高考试题的解法赏析

●

(蒙自高级中学 云南蒙自 661100)

一道浙江省数学高考试题的解法赏析

●苏保明

(蒙自高级中学 云南蒙自 661100)

在解题中常会遇到一类带条件的最值问题，此类问题的解决难度不大，只要认真审题仔细推敲，便会找到许多解法，这也充分体现了高考试题考查学生掌握数学思想方法的功能.

例1若正数x,y满足x+3y=5xy,则3x+4y的最小值是 ( )

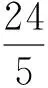
(2012年浙江省数学高考文科试题)

该题是一道很具灵活性与挑战性的高考试题，它蕴含着多种解题方法.本文介绍8种方法，仅供参考.

解法1常数代换法

因为x+3y=5xy，且x>0,y>0，所以

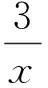
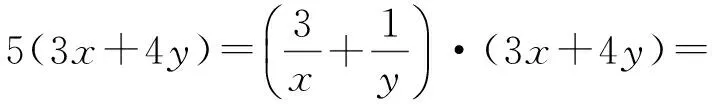
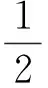
3x+4y≥5,

故3x+4y的最小值是5.

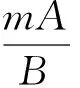
解法2三角法

因为x+3y=5xy,且x>0,y>0，所以

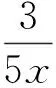
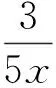
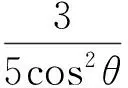
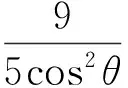
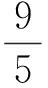
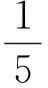
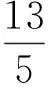
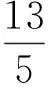
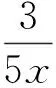
3x+4y≥5，

故3x+4y的最小值是5.

点评根据已知条件适当引入三角变量，再利用三角恒等变换和三角函数的性质进行求解.

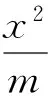
因为x+3y=5xy，且x>0，y>0,所以

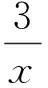
即

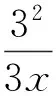
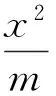
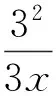
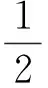
3x+4y≥5，

故3x+4y的最小值是5.

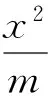
解法4向量法

因为x+3y=5xy，且x>0,y>0，所以

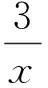
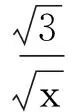
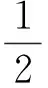
从而

3x+4y≥5，

故3x+4y的最小值是5.

点评通过构造向量，利用向量数量积不等式|m·n|≤|m|·|n|解不等式最值问题，能使运算过程简洁明了.

解法5柯西不等式法

因为x+3y=5xy，且x>0,y>0，所以

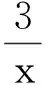
由柯西不等式，得

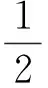
即

3x+4y≥5，

故3x+4y的最小值是5.

点评根据试题本身的结构特征，通过柯西不等式，可使解决过程简便，解答通俗易懂，值得推广和应用.

解法6导数法

因为x+3y=5xy，且x>0,y>0，所以

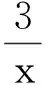
即

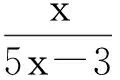
又因为

所以

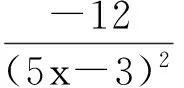
令f′(x)=0，则

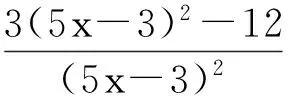
解得

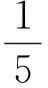
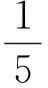
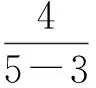
故3x+4y的最小值是5.

点评构造一元函数，将原问题转化为函数的最值问题，再通过求导和利用函数的单调性，使问题得到圆满解决，体现了导数法的解题功能.

解法7巧用数学期望EX2≥(EX)2

因为x+3y=5xy，且x>0,y>0，所以

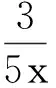
构造离散型随机变量X的分布列(见表1)：

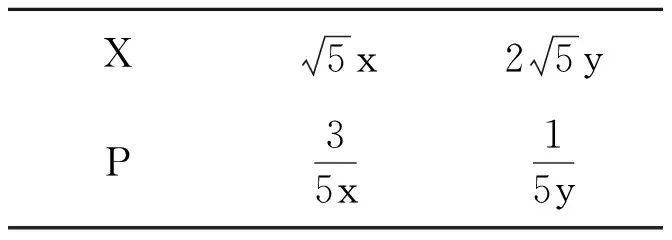
表1 X的分布列

3x+4y，

由EX2≥(EX)2得

3x+4y≥5，

故3x+4y的最小值是5.

点评构造离散型随机变量X的分布列，再根据方差的性质EX2≥(EX)2，使问题顺利解决，利用方差的性质解题的关键是能正确构造离散型随机变量X的分布列.

解法8极坐标法

因为x+3y=5xy，且x>0,y>0，所以

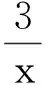
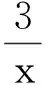
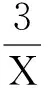
把X=ρcosθ,Y=ρsinθ(0≤θ<2π)代入X+Y=5,得