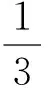由一道“变态”高考题的几组解法引起的教学反思
●
(安丰中学 江苏东台 224221)
由一道“变态”高考题的几组解法引起的教学反思
●崔志荣
(安丰中学 江苏东台 224221)
1 一道“变态”的高考题
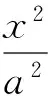
图1
(1)求椭圆的方程.
(2)设点A,B是椭圆上位于x轴上方的点,且AF1∥BF2,点P为AF2与BF1的交点.
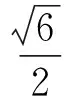
②求证:PF1+PF2是定值.
(2012年江苏省数学高考试题)
笔者对这道高考题的解法作了一些研究,得到了一些有关解析几何复习的教学体会,和读者交流.
2 几组解法的评析
第Ⅰ组 ①解设直线AF1的方程为
x=my-1,
联立
消去x整理得
(m2+2)y2-2my-1=0,
解得

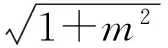
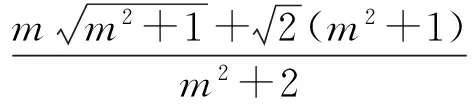
同理

因此

解得
m2=2,
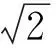
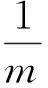
②证明由AF1∥BF2,知
△PAF1∽△PF2B,
从而
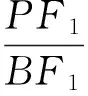
即
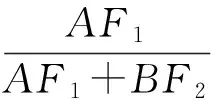
同理

因此
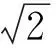
由第①小题知
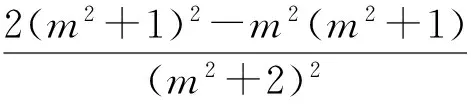
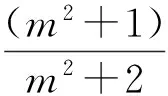

故
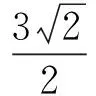
点评第①小题通过联立直线与椭圆的方程,求出点A,B的纵坐标,再用两点间的距离公式求长度,也可以设直线的点斜式方程,求点A,B的横坐标(可由AF1>BF2,利用xA>-1,xB>1来舍根).这种方法是容易想到的,但很多学生未付诸于行动,担心难于运算,这也与平时教学有关,很多教师不重视这种方法.第②小题充分利用了转化思想,抓住相似三角形,把PF1+PF2转化为AF1与BF2表示,在第①小题的基础上才能完成.
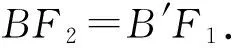
y=k(x+1),
联立
消去y整理得
(1+2k2)x2+4k2x+2k2-2=0,
从而
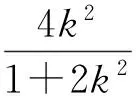
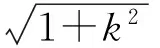
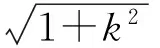
(因AF1∥BF2且AF1>BF2,易知x2<-1 解得 即 设P(x,y),则 式(1)-式(2)得 解得 代入式(2),得 化简得 因此点P的轨迹为椭圆,焦点正好为F1与F2,故 点评第①小题巧用对称性,只需要考虑直线AF1与椭圆联立来研究点A与点B′的横坐标关系,使运算量大大减少.第②小题的解答与第①小题没有必然的关联,如何思考使用轨迹的方法呢?结论要证明PF1+PF2为定值,而F1,F2为定点,那么动点P的轨迹应是椭圆,故设点P(x,y),再利用相似把它转移到点A,B的坐标后代入椭圆方程,最后消去参数λ,求出点P的轨迹方程. 第Ⅲ组 ①解设A(x1,y1),B(x2,y2),则 由焦半径公式,得 从而 因为AF1∥BF2,所以 从而 即 化简得 2x1x2+3(x2-x1)-4=0. 解得 从而 即 ②证明设△APF1与△F2PB的相似比为λ,则 若x1=-1,则x2=1,λ=1,结论成立.若x1>1,则x2>1(若x1<1,则x2<1),因为 (k为直线AF1的斜率),所以 解析几何作为一种重要的数学思想方法,一直都是高考的重点和热点之一,这部分内容也格外受到教师和学生的重视.但一个不容否认的事实是:教师感到这部分内容的教学效果不如人意,学生似懂非懂,解题出错率非常高.结合以上3组解答,笔者对解析几何的教学提几点建议: (1)重基本思路,重基础运算 比较第①小题的3种方法可以发现,第Ⅰ组为基本方法,学生容易理解,教学中不可轻视这种基本思路的讲解,但它的运算量偏大,学生不敢动笔,说明基础运算是教学中的一个大问题.在平时教学中,教师若走捷径,走技巧运算,则会造成学生眼高手低,基础不牢,使学生在考场上总想容易的方法,容易导致失败.据此,笔者认为在解析几何教学中,要重视基本方法的剖析,淡化技巧方法的讲解,淡化特技运算,重视基础运算. (2)代数方法为主,几何方法为辅 解析几何的本质是用代数的方法解决几何问题,解题结构为:几何问题→代数问题→代数研究→几何结果,几何法不应是解析几何的教学重点. 从3组解法中可以看出,第Ⅱ组的第①小题用到了几何对称性,第②小题由于AF1∥BF2都用到了三角形相似的知识,但这些几何知识在解答过程不起主导作用,也是基础知识,是必要的辅助.有些经验丰富的教师,了解不少解析几何题的几何背景,课堂上能把问题一步剖析到最简洁的几何方法,但实际上是效果不大,原因是很少有学生了解高考题的背景,还是要脚踏实地用好代数方法. (3)重分析,重比较 在解析几何中,很多题是有多种方法的,它们的思路不相同,实际计算效果也不一样.因此,教学中要做到2点:一是重思路的分析,如本文中的第②小题,第Ⅰ组解答建立在第①小题的基础上,将PF1+PF2转化为AF1和BF2,第Ⅱ组则是由结论分析到轨迹思路,第Ⅲ组是借助焦半径后运用转化,都是合理的分析;二是重视方法的比较是必要的,如第①小题的3种方法,第Ⅱ组方法灵活,运算简便,第Ⅰ、Ⅲ组是基本方法,运算量都大.只有通过比较,才能使不同层次的学生有他们自己的选择,才能使他们更准确的认识问题的本质,才能使他们在解题时游刃有余. (4)重过程的步骤,重针对性的训练

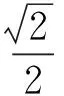



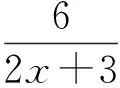
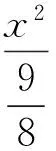
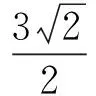

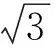

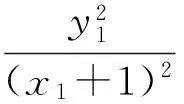
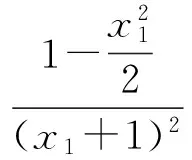
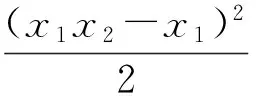
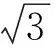
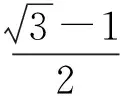
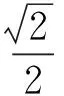

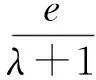

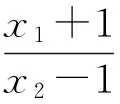
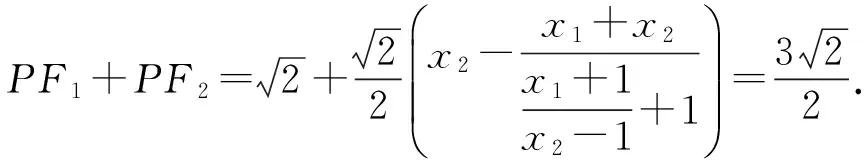

3 几点教学反思