海阔凭鱼跃 天高任鸟飞——2012年浙江省数学高考阅卷有感

●

(元济高级中学 浙江海盐 314300)

海阔凭鱼跃天高任鸟飞
——2012年浙江省数学高考阅卷有感

●甘建飞

(元济高级中学 浙江海盐 314300)

笔者有幸参加了2012年浙江省数学高考阅卷工作，对学生的解题感触颇多：有功亏一篑的扼腕叹息；有势如破竹的畅快淋漓；有无可奈何的黯然喟然；更有那不期而遇的妙笔生花，带来如陈酒般的醇香清洌.而唯有醇之悠长，让人回味无穷.本文就部分妙解，与大家共飨.

1 用好错误解答，凸显数学功底

例1 已知箱中装有4个白球和5个黑球，且规定：取出一个白球得2分，取出一个黑球得1分.现从该箱中任取3个球(无放回，且每球取到的机会均等)，记随机变量X为取出此3球所得分数之和.

(1)求X的分布列；

(2)求X的数学期望E(X)．

(2012年浙江省数学高考理科试题)

解题片断记X为取到白球的个数，X的可能取值为0，1，2，3，则X的分布列为(见表1)：

表1 X的分布列

故

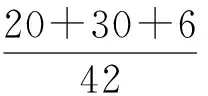
该生一看，审题有误：随机变量X为取出此3球所得分数之和，而解答时记X为取到白球的个数了.学生灵机一动，将X改为Y，继续作答：

记Y为取到白球的个数，Y的可能取值为0,1,2,3，则Y的分布列为(见表2)：

表2 Y的分布列

故

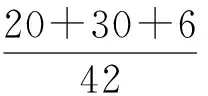
(1)由Y的分布列可得X的分布列(见表3)：

表3 X的分布列

(2)由题意，X=2Y+3-Y=Y+3，则

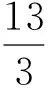
点评1 不得不佩服该生的随机应变能力,利用“错解”中的“有用结论”，化腐朽为神奇，成功地将“错解”扭转为“妙解”.

另外，在本题的解答上，除有些学生审题不清，误以为是“放回模型”外，以下解法却不容阅卷教师小觑.

因为X=2Y+3-Y=Y+3,所以

点评2 超几何分布与二项分布的期望相同是一个既成事实，但由于缺少教材支持，中学数学教学是有意回避的，不过仍有部分学生“知道”这个事实.关于该结论的推导，有兴趣的读者可以查阅文献[1].

2 高思维水平学生的舞台

2.1 动中取静，信手拈来

(1)求tanC的值；

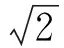
(2012年浙江省数学高考理科试题)

解题片断(1)略.

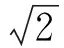
由正弦定理,得

b=c.

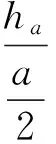
解得

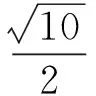
故

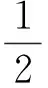
点评该生抓住了“三角形中某条边与某条边的对角为定值时，该三角形的外接圆为定圆”这一特性，找到了“三角形系”的共性，并通过几何图形，化抽象为具体，使动态问题“跃然纸上”，并从动态出发，化动为静，通过简单的运算就完成解答，让人耳目一新.

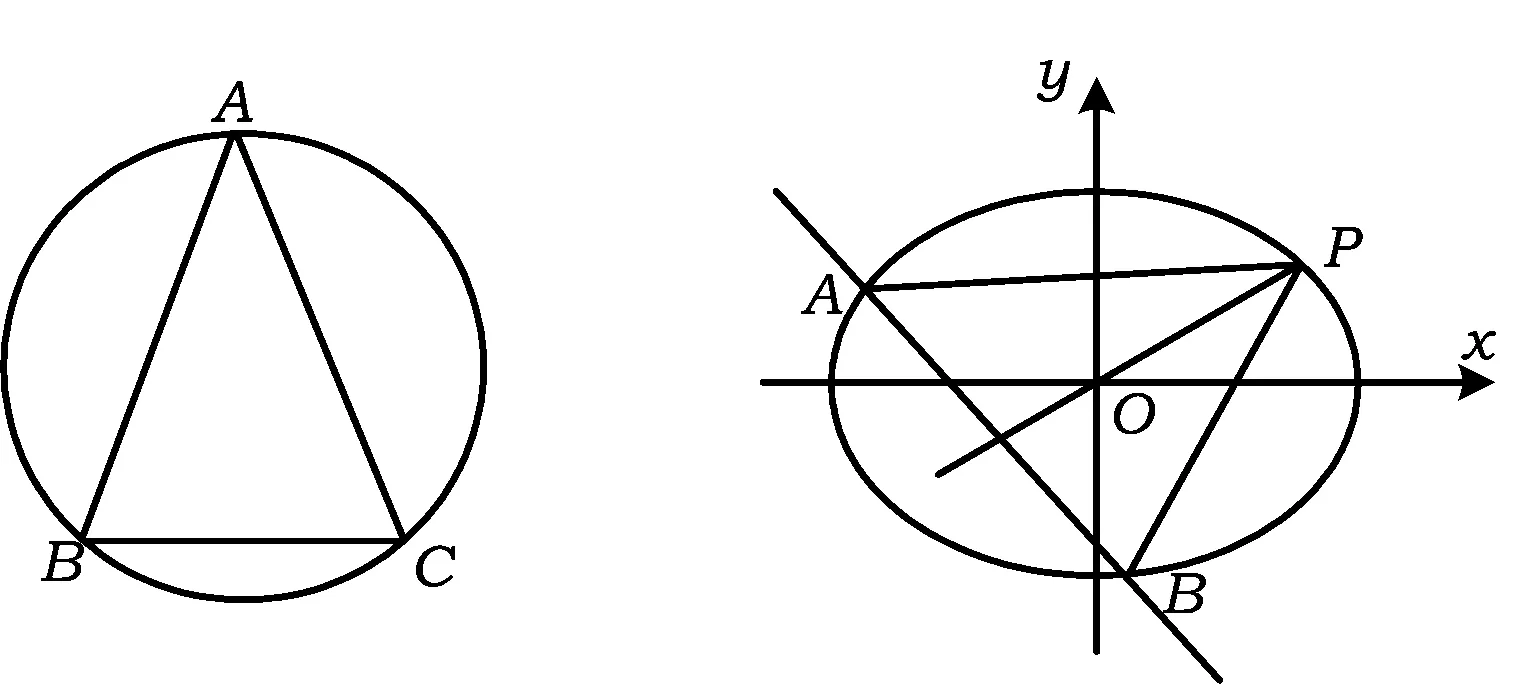
图1 图2

2.2 因式分解并非“巧合”

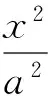
(1)求椭圆C的方程；

(2)求△ABP面积取最大值时直线l的方程.

(2012年浙江省数学高考理科试题)

解题片断(1)略.

(2)在该小题的解答中，

u′(m)=-4(m3-6m2+2m+24)

的因式分解是难点.除了少数学生“试根”成功，发现m-4是多项式的一个因子外，更多的学生对此束手无策，缺少试根的方向，使解题陷入了困境.但也有部分学生处变不惊：

若m-m0是多项式的一个因子，则

m0∈{±1,±2,±3,±4,±6,±8,±12,24},

经验证m0=4成立，所以

m3- 6m2+2m+24=

m3-4m2-2(m2-m-12)=

(m-4)(m2-2m-6).

点评1 对于n次整系数多项式：

anxn+an-1xn-1+…+a1x+a0，

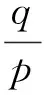
点评2 求面积公式的几种方法.

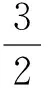
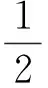
注意到∠PMA为定值，因此决定面积大小的是|AB|·|PM|的大小.

图3 图4

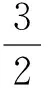
S△ABP=S△ABN-S△PBN=

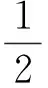
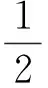
面积的计算是一个常规问题，大多学生不假思索“悟到”了参考答案的计算方法，上述学生“艺高人胆大”，能在高考时尝试“优化”面积的计算方法，难能可贵.

3 摆脱思维定势，绽放思维火花

3.1 立体几何妙用平面向量

(1)证明：MN∥平面ABCD;

(2)过点A作AQ⊥PC，垂足为点Q，求二面角A-MN-Q的平面角的余弦值.

(2012年浙江省数学高考理科试题)

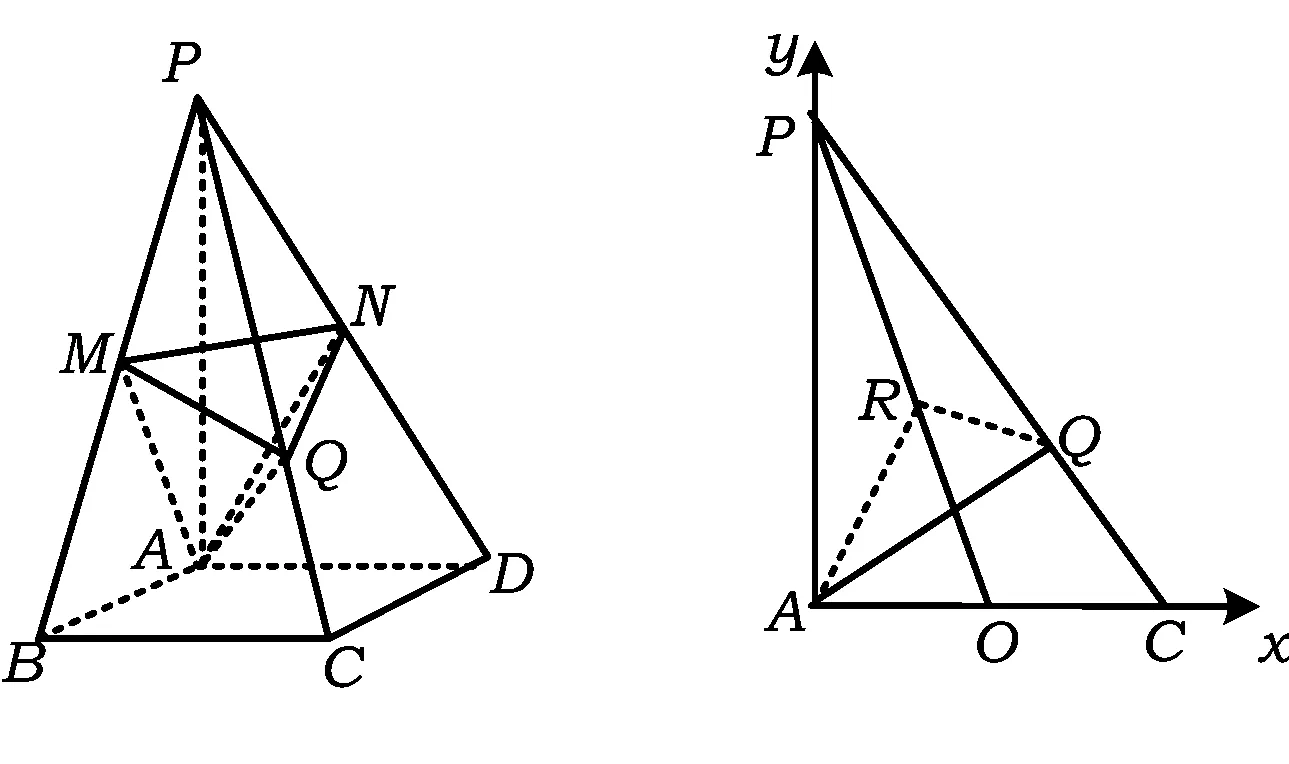
图5 图6

解题片断本题第(2)小题平面角的寻找相对容易，但计算繁琐.有学生不拘泥于通法，借助直角三角形的特性，巧用平面向量工具求解：

取线段MN的中点E，联结AE，EQ,易得∠AEQ为二面角A-MN-Q的平面角.

如图6，设O为AC的中点，易得E为PO的中点，分别以AC,AP为x,y轴建立直角坐标系xAy，则

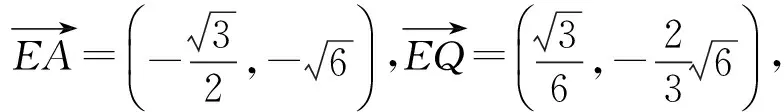
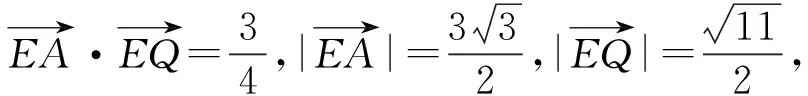
故

点评立体几何方法通常分为常规几何方法和空间向量方法.本题向量法计算量较大，使用常规几何方法，二面角的平面角虽容易找到，但3条边的长都算出来却不容易.该生能从常规几何方法入题，在计算上“移花接木”，用平面向量解决计算问题，大大减少了运算量.

3.2 导数问题，未必求导

例5 已知a>0,b∈R，函数f(x)=4ax3-2bx-a+b.

(1) 证明：当0≤x≤1时，

①函数f(x)的最大值为|2a-b|+a；

②f(x)+|2a-b|+a≥0.

(2)若-1≤f(x)≤1对x∈[0,1]恒成立，求a+b的取值范围.

(2012年浙江省数学高考理科试题)

解题片断本题第(1)小题，大多学生是通过求导和研究函数图像求解，也有学生另辟蹊径：

令g(x)=4ax3-2bx-a+b-|2a-b|+a.

当2a-b≥0时，

g(x)=(x-1)[4ax2+4a-2(2a-b)].

因为x≤1，a>0，2a-b≥0，所以g(x)≤0(当且仅当x=1时取到等号)．

当2a-b<0时，g(x)=x(4ax2-2b).

因为x≥0，4ax2-2b≤4a-2b<0,所以g(x)≤0(当且仅当x=0时取到等号)．

综上所述,

f(x)≤|2a-b|+a.

点评该生将函数的最大值问题转化为不等式的恒成立问题，摆脱了“导数题必求导”的思维定势，并能考虑到不等式成立与函数最大值的差别，思路之开阔，表述之严谨，令人称道.

[1] 李辉.二项分布若干性质的思考[J].中学教研(数学)，2011(3)：21-23.