地面连续测量轮轨垂向力的方法

洪溢颺， 林建辉

（西南交通大学牵引动力国家重点实验室， 四川成都 610031）

0 引言

轮轨关系是轨道交通中的一大重要关系，严密关系到列车运行安全，当轮轨力异常时，可能导致列车脱轨。为了保证列车运行安全，有必要严密监测轮轨垂向力和横向力。现有的轮轨力测量方法主要有测力轮对、测力钢轨等[1]。但测力轮对和测力钢轨都需安装专门的轮对和钢轨，不便于在既有线路上普遍连续测量，本文以轨道结构力学分析为基础，就地面连续测量轮轨垂向力的方法进行讨论。

1 轮轨关系中的若干力学问题

轮轨关系中的力学问题极为复杂，轨道列车这种交通形式完全是依靠轮轨接触实现。轮轨接触包括轮轨滚动、蠕滑、黏着、摩擦等等一系列复杂力学问题[2-3]。图1为轮轨系统受力示意图。

图1 轮轨系统受力示意

2 刚性支座上多跨、等距均截面连续长梁求解

为求解弹性无限长梁的支座反力解的问题，先考察刚性支座上多跨、等距均截面连续长梁的解。考虑对称加载情况[4]。如图2所示。

图2 对称加载计算简图

当为连续无限长梁时，支座上力矩表达式为：Mr=C1qr1；其中C1为待定常数。如图2所示，在0-0-1跨上，由力学三弯矩方程有：

以上便是集中荷载作用下，刚性连续等跨无限长梁各支座反力的解。当荷载为偏载时，可以以叠加法或者直接求解法求解其待定系数。

3 弹性支座上多跨等距均截面连续长梁求解

钢轨结构由钢轨、轨枕、连接件、道床、防爬器、轨距拉杆、道岔等组成[5]。钢轨受到来自于列车轮对的垂向、横向荷载作用和冲击作用，以及来自于枕木和扣件的支承作用等，再加之垂向力、横向力不一定作用于轨面几何中心，其受力行为较为复杂。受力模式见图3。

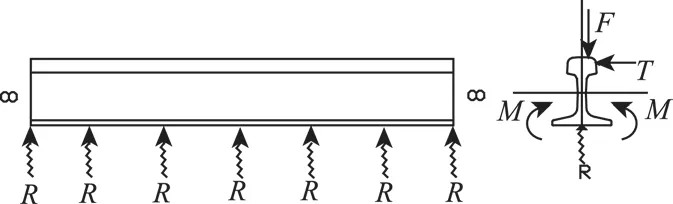
图3 轨道结构受力简图

轨道静力计算通常采用连续弹性地基梁和连续弹性点支承梁两种计算模型。本文采用弹性支座上多跨、等距、均截面梁模型进行轨道结构力学分析与计算[2]。

取弹性支座上一个多跨等距均截面连续梁，跨上无任何荷载，如图4所示。

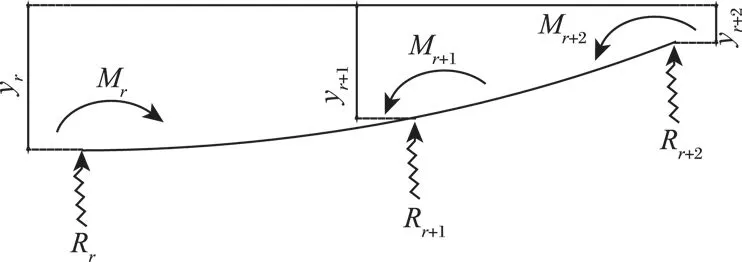
图4 弹性地基梁计算简图

其三弯矩方程为：

上述方程组的求解过程较为繁琐，其解法有多人做过研究并给出了详细的求解，不再赘述。通过编制好的待定系数表，可以方便求得各支座处弯矩值及支反力值，这一理论为本文构想的通过测试轨枕反力的方式测量轮轨力提供了理论可行性。

4 地面连续测量轮轨垂向力的方法

通过上述理论分析计算可知，当得知轨枕反力R时，可反算求得轮轨作用荷载W。关键问题在于钢轨为无限长梁，枕木也有无限多个，因此需要考虑的一个关键问题是取多长区段的轨枕反力合力作为计算值能够得到较为精确的轮轨垂向荷载作用力。

设轮轨垂向力作用在钢轨某r—r+1跨上，根据轨道结构力学分析计算可得，其主要支反力在左右相临5跨以内。因此，可在测试跨及前后5跨内布置测力垫板，测试轨枕反力R，再由公式：，即可求得轮轨在某一跨钢轨内的任意位置轮轨力数值（见图5）。

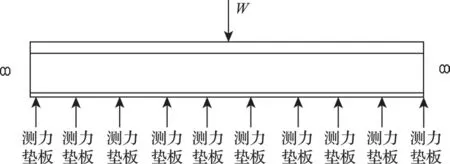
图5 测试方法示意

5 算例

本文采用大型通用有限元结构计算软件ABAQUS，对钢轨进行有限元分析，模拟钢轨受力形态，分析轨枕支承反力分布情况，验证测试方法可行性[7-8]。该模型将轮轨接触面网格细化，模拟轴重40t货车在某一跨上加载。计算结果显示，支承反力大多分布在加载跨左右五垮范围内（见图 6）。

图6 钢轨有限元分析

6 结论与展望

通过上述理论计算发现，由测轨道支承反力的方法连续测量垂向轮轨力是可以实现的。不足之处在于测试精度和轨枕可能失效的问题，一旦轨枕失效，轨底支承反力会重新分布，该测试方法会产生一定误差，这些问题有待进一步研究改进。

[1] 陈建政.轮轨作用力和接触点位置在线测量理论研究[D].成都:西南交通大学,2008.

[2] 王惠银,步启军.轮轨关系与磨[J].铁道建筑,2007(1):82-83.

[3] 金学松,张雪杉,张剑,孙丽萍,王生武.轨关系研究中的力学问题[J].机械强度,2005,

[4] 谢天辅.铁路轨道结构静力计算问题[M].北京:人民铁道出版社,1979:20-27.

[5] 练松良.轨道工程[M].上海:同济大学出版社,2006:193-194.

[6] 段明德,李德基.等跨距三弯矩方程组的通解[J].力学与实践,1982(5):59-61.

[7] 黄志辉,赵红伟.钢轨应变分布场的有限元分析[J].机电工程,2007(4):13-15.

[8] 郜永杰,翟婉明.轨道结构强度有限元分析[J].交通运输工程学报,2004(1):36-39.