基于AF策略的高斯正交不信任中继信道的最优资源分配

郁章菊

（南京邮电大学通信与信息工程学院, 南京 210003）

0 引言

无线通信表示任何人可以在任何地点同外界进行通信，其也成为人们生活中必不可少的一部分。同时由于无线通信具有广播特性，因此信息传输过程中很容易被窃听者窃取。传统的通信安全协议是用过计算性来保障安全性的，都是假设窃听者的计算能力受限的情况下，因此这种方式并不是绝对安全的。如果窃听者能够获得足够的信息，并利用计算机穷举法就能够得出密钥，从而获得秘密消息，使得通信过程不安全。因此如何保障无线通信过程中的信息安全成为研究热点。香农提出基于信息论基础的安全通信[1]，分析安全通信系统模型。在文献[2]中，Cover给出了中继信道的信道容量，证明了中继节点对源节点起协作作用，通过节点间的协作提高了信道的可达速率。Wyner提出了窃听信道的概念[3]，并确定了发送方和接收方之间不依赖于密钥而进行的几乎绝对安全通信的可能性。Csiszar和Korner[4]推广了Wyner的工作，研究了在广播信道上传输秘密消息（confidential message）系统下的理论信息安全问题。Lai Lifeng在文献[5]中提出了4节点的中继窃听信道，中继节点可以协作源节点到目的节点使得系统能够实现安全通信。在文献[6-13]主要讨论了不同系统模型的安全速率及不同系统模型进行资源分配，通过采用不同的分配策略，提高系统的安全性能。

本文针对考虑两种模型安全性能。针对高斯正交不信任中继信道模型2，采用放大前传策略，考虑系统的安全速率问题，假设系统信道总带宽及源节点发射功率受限的情况下，提出一种最优的资源分配策略。最后在MATLAB环境中进行仿真得到最优资源分配策略下的的安全速率，同时给出使用不同策略分配的安全速率进行比较。仿真结果表明，本文提出的最优资源分配策略具有更高的安全速率，并且证明了最优资源分配策略方案能够提高系统的安全性能。

1 系统模型

在图1中，源节点是以广播形式向中继节点和目的节点发送消息，图中用实线表示信道1，用虚线表示信道2，两个信道相互正交。源节点发送的信号表示为X，中继节点输出的信号为Xr，中继节点接收的信号表示为Yr，目的节点接收来自信道1的信号表示为YD，接收来自信道2的消息表示为YR。假设信道概率分布满足：

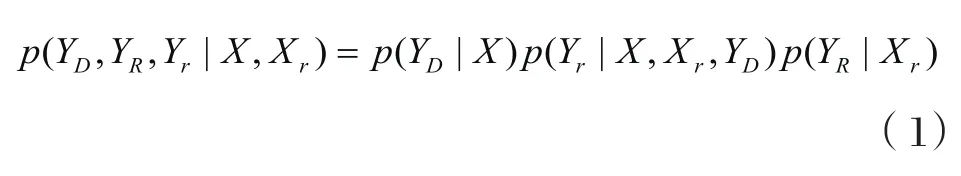
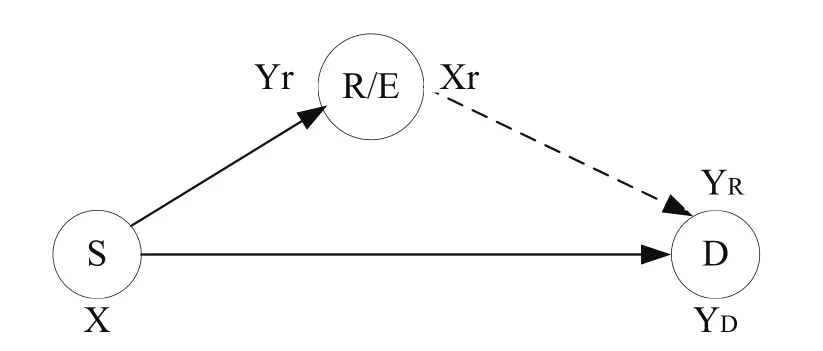
图1 具有正交分量的中继信道模型

假设信道是离散无记忆的，信道1和信道2的输入信号和输出信号之间的关系表示为：

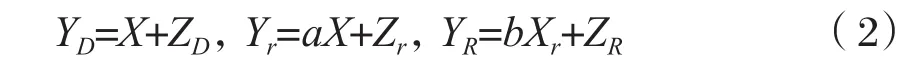
其中ZD, Zr, ZR分别是均值为0，方差为1的独立同分布的高斯随机变量，a, b分别表示源节点到中继节点及中继节点到目的节点的信道增益。假设源节点和中继节点的最大发射功率分别为P和Pr，则源节点和中继节点的传输功率满足约束表示为：

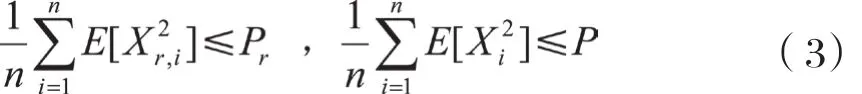
2 最优资源分配策略下的可达安全速率

假设总的可用信道带宽为Wmax赫兹，由乃奎斯特定理知，每秒钟的信道资源为2W赫兹，把2Wmax带宽资源分配到两个正交信道中。假设信道1和信道2分配相同的带宽，用W表示分配到两个信道的带宽。我们考虑中继节点使用AF（amplify-and-forward）策略的情况。假设源节点的平均传输功率为p，中继节点在第i信道上传输的信号表示为：

定理1： 对于由式(5)给出的高斯正交不信任中继信道模型，对于任何给定的满足约束条件的功率p，存在唯一最优的W*，使得式(5)有最大的可达安全速率。

注释1 Ivana M在文献[12]中，给出了使用AF策略下的中继问题的最优解。同时给出了最优带宽W*，最大的安全速率r*，总功率p的线性关系。

因此从式(5)和文献[12]中，我们可以得出式(5)的最优解。同时给出最优带宽W*,最大安全速率Rs*和源节点的发射功率p存在如下的非线性关系：

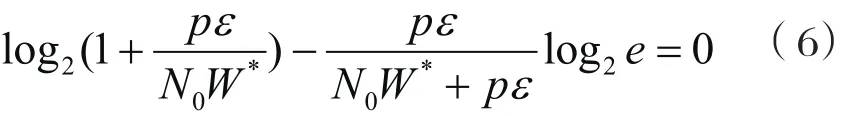
3 仿真结果

为了说明采用最优资源分配策略对系统安全性能的影响，现在将对不信任中继高斯正交信道模型的可达安全速率进行验证仿真。假设信道资源（源节点信号传输功率及信道带宽）最大分配时，在MATLAB环境中仿真得到最优资源分配和最大资源分配策略进行对比分析，进而分析说明最优资源分配策略能够提高系统的安全性能。

在图2中给出了最优源节点功率分配情况下的可达安全速率，通过图示结果说明对于任何给定的信道带宽满足0≤W≤Wmax，Rs(W,p)是关于W严格的凸函数。由凸函数的性质知，存在唯一的W，使得达到最大安全速率。

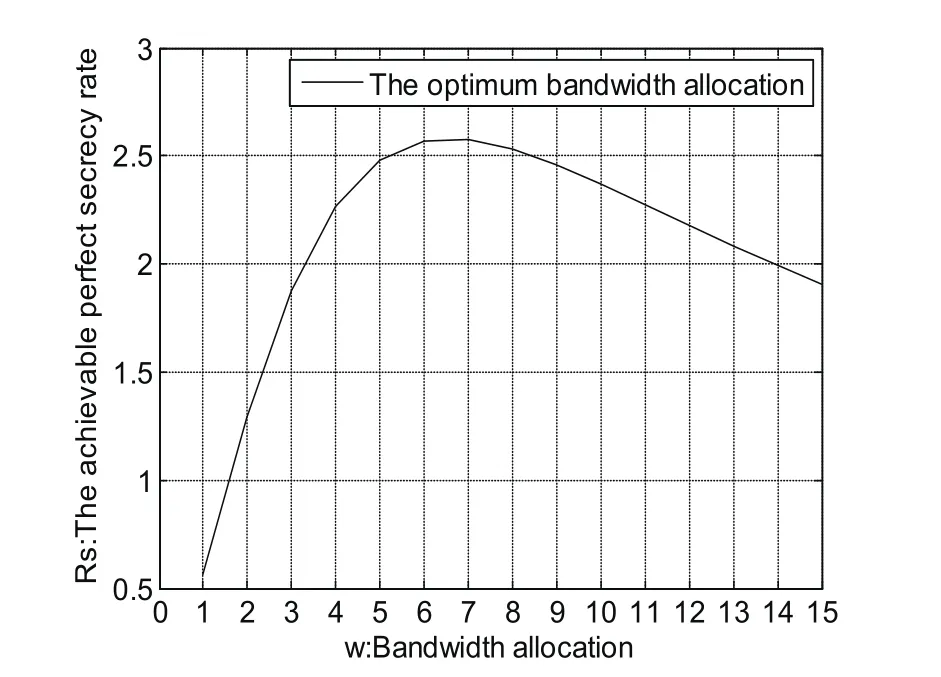
图2 可达安全速率随带宽变化情况

在图3中给出信道带宽分配比较，即采用最优信道带宽分配与最大信道带宽分配的可达安全速率的对比。从图中可以看出，当信道的分配的带宽从零变到最大时，采用最优资源分配方案能到的安全速率比最大资源分配策略得到的安全速率大，因此最优资源分配可以很大程度的提高系统的安全通信性能。

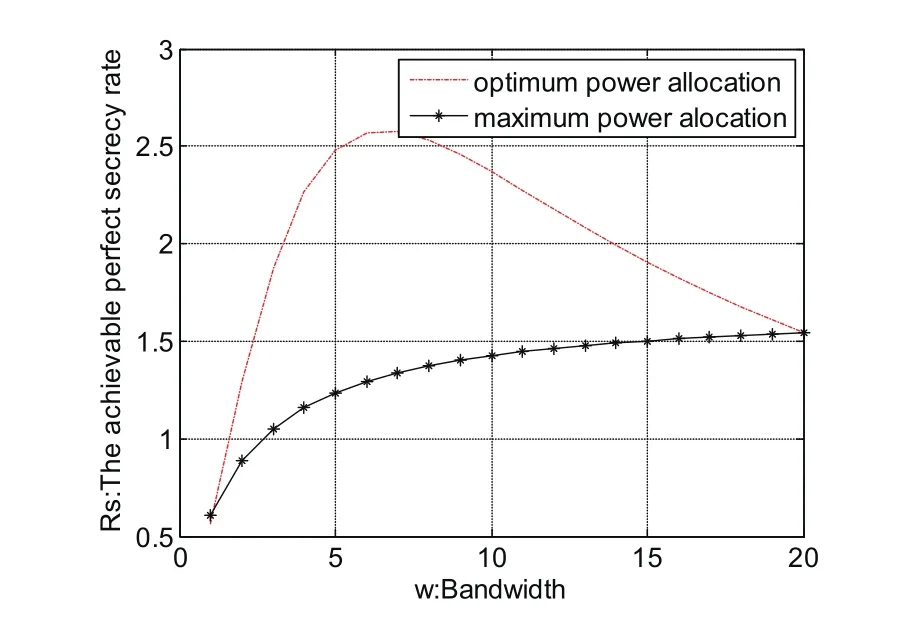
图3 最优带宽分配方式与最大带宽分配方式到的可达安全速率的比较情况

[1] C. E. Shannon.Communication theory of secrecy systems[J].Bell System Technical Journal,1949,28(4):656-715.

[2] T. Cover,A. E. Gamal.Capacity theorems for the relay channel[J].IEEE Transactions on Information Theory,1979,25(5):572-584.

[3] A.D.Wyner.The wire-tap channel[J].Bell System Technical Journal,1975,54(8):1355-1387.

[4] I. Csiszar ,J. korner.Broadcast channels with confidential messages[J].IEEE Transactions on Information Theory, 1978,24(4):451-456.

[5] L. Lai,H. El Gamal.The relay-eavesdropper channel: Cooperation for secrecy[J].IEEE Transactions on Information Theory,2008,54(9):4005-4019.

[6] X.He,A.Yener.Cooperation with an untrusted relay:A secrecy perspective[J].IEEE Transactions on Information Theory,2010,56(8):3807-3827.

[7] A.El Gamal,S.Zahedi.Capacity of a class of relay channels with orthogonal components[J].IEEE Transactions on Information Theory,2005,51( 5):1815-1817.

[8] Y.Kim.Capacity of a class of deterministic relay channels[J].IEEE Transactions on Information Theory,2008,54(3):1328-1329.

[9] X.He,A.Yener. On the equivocation region of relay channels with orthogonal components[J].IEEE Transactions on Information Theory archive,2010,56(8):3807-3827.

[10] V.Aggarwal,L.Sankar,A.R.Calderbank,H.V.Poor.Secrecy capacity of a class of orthogonal relay eavesdropper channels[J].EURASIP Journal on Wireless Communications and Networking, 2009.

[11] Y.Liang,V.V.Veeravalli.Gaussian orthogonal relay channels:Optimal resource allocation and capacity[J].IEEE Transactions on Information Theory,2005,51(9):3284-3289.

[12] I.Maric,R.D.Yates.Bandwidth and power allocation for cooperative strategies in gaussian relay network[J].IEEE Transactions on Information Theory,2010,56(4):1880-1889.

[13] Y.Oohama.Coding for relay channels with confidential messages[R].in Proc. Inf. Theory workshop, sep.2001.