大学一年级学生创新能力培养探索与实践

杨小远， 李尚志

（1.数学、信息、行为教育部重点实验室，北京； 2.北京航空航天大学数学与系统科学学院，北京 100191）

大学一年级学生创新能力培养探索与实践

杨小远， 李尚志

（1.数学、信息、行为教育部重点实验室，北京； 2.北京航空航天大学数学与系统科学学院，北京 100191）

详细介绍了我们在主讲《工科数学分析》课程中以问题驱动的研究性微积分教学模式和培养学生创新能力的探索与实践.

数学分析；创新能力；研究性微积分教学模式

1 前 言

在每年参加研究生面试的时候，我们喜欢提出这样几个问题：谈谈对有限覆盖定理的理解、Taylor公式的局限性、闭区间套定理的理解、黎慢积分与勒贝格积分的区别、引入函数一致连续概念的意义是什么？它带给我们什么“好处”等.学生的回答让我们感到吃惊，学生对这些概念定理都能准确叙述，但是对数学的认识却一点也没有，竟然回答Taylor公式的局限性是计算复杂，需要计算高阶导数.有限覆盖就是把区间覆盖.这些学生考研究生的数学分析成绩都不错，面对同学们这些回答，让我们思考一个问题，数学教育目的是什么？如果学生将主要精力用于作大量数学题目，死记硬背数学定理和公式，而忽略了对数学问题的本质理解，这应该是数学教育的失败.近几年，我们一直在探索新的教育模式，工科数学分析课程建设所做的全部努力是让学生对数学问题知其然，又要知其所以然，废除以作题为主的学习模式.为此我们倡导并实践以问题驱动的研究性微积分教学模式，提出并实践设置系列探索类问题.学生的学习过程不在是单一的学习过程，而是不断思考、探索和发现的过程.下面详细介绍我们的教学研究与实践.

2 大学一年级学生创新能力培养模式的探索与实践

2.1 让学生对数学问题知其然又要知其所以然.

本文第二作者在他最新出版的《线性代数》书中写到，数学不是“奉天承运皇帝诏曰”从天而降的抽象定义和推理，而是一部由创造发明的系列故事组成的连续剧［1］.在他主持的国家精品课程《数学大观》视频讲座中，提出思想（idea）指挥技巧（Technique）.数学的教学要引起学生对数学的兴趣，让学生爱数学［2］.在教学过程中罗列知识，仿佛这些定理是“奉天承运皇帝诏曰”从天而降，学生很难对数学感兴趣.要让学生对数学问题知其然又要知其所以然，才能引起学生对数学的兴趣.例如为什么引入函数一致连续概念？为什么引入函数项级数的一致收敛概念？这些概念能带给我们什么？在教学过程中，要引导学生对这些问题的认识，函数一致连续使得弧长、曲线、曲面积分计算理论严谨化，函数一致收敛是有限次极限，求导和积分的运算法则推广到无穷多次的前提.对实数系六个等价命题的理解，我们以闭区间套和有限覆盖定理来说明.对这两个定理，初学者感到莫名奇妙，不知道为什么提出这两个定理.闭区间套定理实际上是逐步逼近的思想，闭区间套所有的交点是问题的“解”，而闭区间套就是逐步逼近“解”所在的区间，当区间长度趋于零的时候，“解”求出.有限覆盖实际上是将无穷维问题转化为有限问题处理，或者说将逐点问题转化为整体问题.在整个教学过程中，我们用这两个定理解决许多理论和应用问题，使得学生在学习的过程中逐步加深对定理的理解.讲授Riemann积分，那么Riemann积分的缺点是什么？Lebesgue定理告诉我们，Riemann积分对函数的依赖性很强，函数项逐项积分要求函数项级数一致收敛，这样“苛刻”条件在许多实际问题中不能满足，导致Lebesgue积分的提出和研究.在教学过程中，强调对数学问题的本质理解，让学生对数学问题知其然又要知其所以然，这是培养学生创新能力的前提，否则即使将数学分析的定理全部背熟，都等于零，没有意义.

2.2 精炼传统数学分析内容，研究共性问题的教学.

数学分析内容十分庞大，可谓“洋洋大观，琳琅满目”，但是最本质核心的内容并不多.例如多元微积分就是一元微积分的推广，许多结论和证明方法几乎都是平行的.因此必须让学生掌握微积分本质核心问题，注意许多共性问题的学习，抓住本质问题，学生的思路变得清晰.例如在数学分析中任何问题的提出都是以极限形式给出，数列极限，函数极限，导数、微分、定积分、重积分、曲线与曲面积分的定义都是用极限表述的，极限数学化定义是微积分发展史上里程碑的概念，使得微积分形成目前严谨体系.因此数列极限定义的学习和理解是关键，函数极限，导数、微分、定积分、重积分、曲线与曲面积分的定义刻画问题的本质与数列极限一致.数学分析以柯西命名的定理很多，如数列极限收敛的柯西定理，函数极限存在的柯西定理，数项级数收敛的柯西定理，函数项级数一致收敛的柯西定理，广义积分收敛柯西定理，含参变量积分一致收敛的柯西定理，面对如此多的柯西定理，学生经常不知所措，引导学生把握这些定理的共性问题，虽然他们描述不同数学问题，实际上刻画问题的思想是一致的，都是研究问题自身变化规律.这些柯西定理，数列极限的柯西定理是基础，其余都是推广.同样判断数项级数收敛、函数项级数一致收敛、广义积分收敛、含参变量积分的一致收敛的狄里克莱和阿贝尔判别方法的都是相应问题柯西定理思想的延伸，刻画问题的思想是一致的.数学分析中有几个概念学生理解起来十分困难，例如函数的一致连续，函数项级数的一致收敛，含参积分一致收敛，刻画这些概念“一致”性的数学特征是相同的.在教学过程中，引导学生抓住本质问题，使得数学的学习变得轻松.

2.3 将微积分经典内容进行拓展与延伸，力求反映当代数学的发展趋势.

精炼了传统数学分析内容的同时，增加数学的应用背景，力求为学生打开应用数学的窗口，让抽象的数学变得具体，同时注重数学分析经典内容与现代应用数学分支的联系，以开阔学生的视野.数列极限部分，增加了数列极限的应用实例，如自然界中的混沌现象，这使得学生在掌握极限基本理论的同时，了解了新的数学分支.在函数极限与连续一章，介绍了连续函数压缩映射原理.在此基础上介绍了不动点理论在非线性方程求根中的应用，同时介绍了非线性方程求根的几个基本理论问题：算法的收敛速度和局部与全局收敛问题，这样学生对无穷小阶的运算有全新的认识.Taylor公式是微积分的经典内容，我们没有停留在介绍Taylor公式和其简单应用，而是通过利用Taylor公式与导数数值计算的介绍，阐述了Taylor在科学计算中的应用，并且给出了更一般结论—李查逊（Richardson）外推.同时，介绍了克服Taylor公式局部逼近的Lagrange插值与误差分析，以及函数的最佳一致逼近问题，让学生对函数数值逼近领域有一个初步的认识，并激发他们进一步深入学习函数逼近的其它内容.在定积分部分，不仅介绍了Riemann可积的达布上和下和定理，而且增加了Lebesgue定理与Lebesgue积分的介绍，加深了学生对Riemann积分的认识，同时了解了Lebesgue积分研究的意义.实际上Lebesgue积分在各个数学分支的应用成了现代数学的一个特征.在微分方程部分，特别强调了数学建模的思想，让学生学会用数学模型描述实际问题并求解.在介绍了几种经典的求解方法的基础上，增加了微分方程数值求解的基本方法和几个基本理论问题：数值解的收敛性和稳定性.在傅里叶级数部分，在介绍经典傅里叶级数和变换的基础上，分析了傅里叶变换的局限性，在此基础上介绍了小波变换和分数阶傅里叶变换基本思想，以及在工程技术领域中的应用.在多元函数极值问题部分，介绍了约束和非约束非线性优化的基本求解方法，使得学生对数值优化理论这一分枝有初步的了解.总之，我们力求在有限的篇幅内，扩展教学的宽度，让学生有更多的发现，体会微积分的作用.但是这些内容不是在理论上任意拔高，将高观点强加给学生，让学生不知所云，而是要遵循学生的认识规律.我们的原则是利用数学分析的知识，使学生能够学懂和理解这些问题，重在强调方法和思想.让学生从开始学基本知识，由不懂到懂，打好基础，然后再逐步将数学问题引向深入，最后达到对数学理解有一定的高度.

2.4 学习与研究必备工具：MATLAB软件.

数学的抽象往往让学生不知所云，难以理解.因此在教学过程中抽象的数学概念和定理的证明思想尽可能用几何直观给予解释.要求学生会用MATLAB软件，这是数学学习和研究的必备工具，下面举例说明.

例1MATLAB软件在分析函数一致连续中的应用.

函数一致连续是数学分析非常重要和难理解的数学概念，要求学生在分析函数是否一致连续的时候先绘图，然后在给出严谨的理论分析，这样学生学起来轻松.

函数

从图像可以初步判断在R上不一致连续，因为两个函数在定义域的区域内图像几乎垂直x轴，然后在此基础上给出严谨的证明，这里从略.

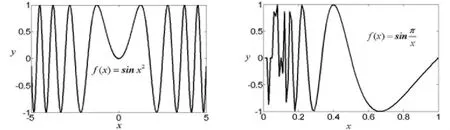
图1

例2图2用MATLAB软件在分析Taylor公式局部逼近特性示意图.

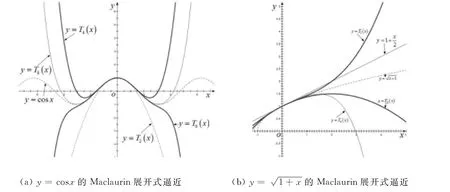
图2

例3MATLAB软件在积分学中的应用.

图3解释重积分概念的示意图，随着分割的不断加密，逐步逼近曲顶体积.

图3

图4是空间曲面uv分割示意图.讨论空间曲面计算问题时候，曲面uv分割是重要的概念.

图4 空间曲面u曲线与v曲线分割示意图

定积分，重积分，曲线与曲面积分的计算是积分学的重要内容，然而这些计算问题的前提是对积分区域数学描述，要求学生在进行各类积分计算的时候，用MATLAB软件绘出积分区域示意图，对积分的计算非常有益处.

2.5 学生创新能力培养模式.

从大学一年级开始我们就对学生进行适当的引导，激发他们的科学研究意识，就《工科数学分析》课程内容设置了系列探索类问题，分为基础研究、应用研究和实践类问题.目的是培养学生养成阅读、思考和探索问题的能力，摆脱中学的题海战术，不要求他们完成数学分析中技巧性和难度过高的题目，而是要求学生将精力集中在对数学概念和本质问题的学习上，鼓励学生尝试更多的探索类问题，引导学生通过数学公式看世界.在我们主讲的班级，学生成立30多个研究小组，每个研究小组3到5人，学生选题完全按照自愿的原则，对感兴趣的问题进行研究.每学期完成1到2个探索类问题，我们的总体思路如下：

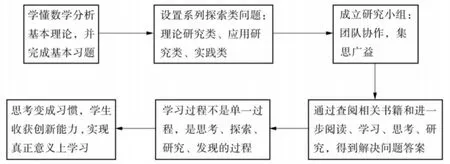
图5

由于篇幅有限，这里部分介绍学生研究情况.

2.5.1 数列极限与混沌现象

数列是数学分析的基础和核心，在学完极限的定义和基本性质以后我们介绍了自然界的混沌现象.通过介绍几个典型问题：三体问题，蝴蝶效应，昆虫繁衍模型，展现混沌现象的产生过程，最后介绍混沌现象的应用.学生对三个具体的混沌模型产生了浓厚的兴趣，在这里数列的极限不再是抽象的概念，而是表述现实世界的数学工具.

关于数列与极限设置了探索类问题：

（i）研究Stolz定理成立的充分必要条件.

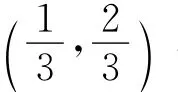
（a）证明被去掉区间的长度之和为1，康托集集合有无穷多个点；

（b）对于二维情况的康托集是按照如下方式进行的.将边长为1的正方形等分9个小正方形，去掉中间的小正方形（开区间），在乘下的8个小正方形中在去掉相应的中间的九分之一，依次类推，证明去掉所有正方形面积为1，但是剩余的点集和康托集集合有无穷多个点；

（c）分析研究上述结论.

（i）闭区间套定理和有限覆盖定理的应用.

（ii）实验课题：关于Logistic序列.在生态学中种群增长的模型是Logistic序列

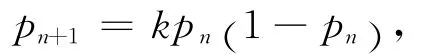
其中pn表示一个单独物种在第n年时规模与种群数量最大值的比值，0≤pn≤1.

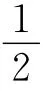
（iv）当3＜k＜3.4，分析序列的变化趋势；

（v）分析3.6＜k＜4序列变化趋势，若取p0＝0.001序列变化趋势.

研究小组对于第（i）个问题进行了研究，研究了多种Stolz定理成立的充分必要条件，研究结果已经被《高等数学研究》录用.问题（ii）是为后续的可数集合和零侧度集合概念作准备，很多学生对这个问题好奇，发表论文见附录2）.对于问题（iii）研究小组在整个数学分析课程的学习过程中积累这两个定理在不同数学问题中的应用，写出了分析报告.问题（iv）通过编程实现，研究小组的学生对混沌现象有个初步感性认识.

2.5.2 函数极限与连续以及压缩映射原理.

讲授了函数的极限与连续的基本理论以后，我们介绍了连续函数的应用：压缩映射原理.为了进一步开拓学生的思路，让学生有更多的想像空间，在课堂上介绍了如果将不动点推广到一幅图像上会怎么样？在此基础上介绍了不动点理论在分形图像压缩中的应用，阐明创新思想的重要性.在这一章我们设置了探索类问题

（i）在目前结论基础上，研究函数一致连续判别方法.

（ii）函数一致连续概念的应用.

（iii）利用分形压缩方法实现下面图像的压缩（压缩比由自己决定）

研究小组针对问题（i），对一元函数和多元函数以及向量函数的一致连续判别方法进行了深入研究，得到了有一定价值的结论，研究成果发表论文见附录1），7），10），12），这个研究小组在整个数学分析的学习过程中一直对这个概念产生了浓厚的情趣，并且就这一概念在曲线积分、曲面积分、重积分、含参积分中的应用写出了分析报告.由于我主讲的班级是计算机专业，有一些编程能力比较强的同学对问题（iii）非常感兴趣，通过进一步查阅相关的书籍，利用分形原理编程实现了图像的高倍压缩.

2.5.3 导数与微分.

导数与微分的教学内容很多，主要是利用导数来研究函数的性质.我们介绍了导数在非线性方程求根中的应用，同时介绍了非线性方程求根的几个基本问题：局部收敛与全局收敛，收敛速度分析.使得学生体会引入无穷小阶概念的重要性，在这一章，我们设置了探索类问题如下：

（i）研究无穷区间上的三个中值定理.

（ii）应用问题研究：通过研究设计环形滑车道.

假设滑道上升部分的斜率为0.8，下降部分的斜率为－1.6，并且两段的直的路径y＝L1（x），y＝L2（x）和一段抛物线y＝ax2＋bx＋c组成，对于光滑的轨道，前进的方向应该是光滑的，因此应该使得三条线段在连接点P，Q处有切线，如图7所示.研究下面问题：

（a）假设P，Q之间的水平距离为100米，求出a，b，c，使得该轨道在连接点处是光滑的；

（b）为了设计更为光滑的曲线，假设连接中间抛物线y＝ax2＋bx＋c两段函数分别用

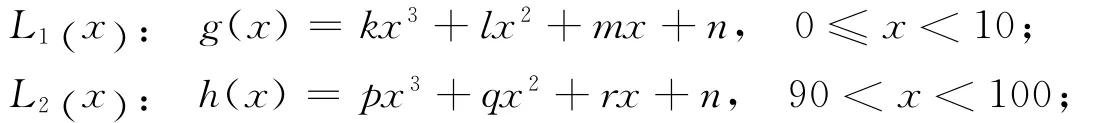
为了确保上面三段函数在连接点的二阶导数相等，研究上面11个未知数的函数关系.

（c）研究设计你喜欢的环形滑车道路.

图7

通过查阅非线性方程数值解方面的书籍和文献学习和研究同伦算法，并写出分析报告.

研究小组对问题（i）进行了深入的研究，得到一些结论，发表论文见附录13）.对（iv）学生设计了自己喜欢的滑行轨道.对问题（v）研究小组通过查阅相关书籍，进一步深入学习，写出了分析实验报告.

2.5.4 Taylor公式与插值逼近初步.

Taylor公式是微积分的经典内容，具有十分重要的理论和应用价值.但传统的教学方法往往过于强调其推理和证明，使学生难以理解其思想精髓.在教学过程中通过Taylor公式在导数数值计算中的简单应用，阐述了Taylor在科学计算中的应用，通过Taylor公式构造更高精度的计算公式—计算数学领域的外推算法.在此基础上给出更一般的结论—李查逊外推（Richardson），同时让学生了解控制舍入误差是科学计算中面临的重要问题.同时讲授了拉格朗日插值和最佳一致逼近问题的相关结论.在这一章，设置了探索类问题.

（i）用李查逊外推（Richardson）研究高阶导数的数值计算.

（ii）1748年，Euler利用

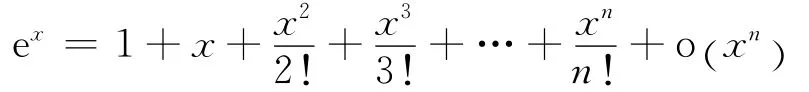
得到e的精度到23位.2000年，Xavier Gourdon仍然用这个公式，得到e的一百二十亿位小数的精度，你能否探索Xavier Gourdon研究方法.

（iii）Taylor公式和Lagrange插值，这是函数逼近理论中的最基本的方法，但是两种逼近方法都有缺陷.读者可以通过查阅函数数值逼近方面书籍，进一步学习样条插值逼近和最佳插值逼近问题，这些逼近方法即保证了逼近的收敛问题.

研究小组针对问题（i）进行了深入研究，研究了高维问题的外推算法，提出了任意阶导数的数值方法，并对算法的性能进行了分析，发表论文见附录8），11）.研究小组对（ii）进行了深入研究，通过查阅大量英文文献，全面总结了历史上各个时期数学家对e的研究成果，对Xavier Gourdon提出的算法进行了学习、分析，分析报告已经被《高等数学研究》录用.这两个学习小组对问题（iii）和（iv）都进一步学习写出分析实验报告.

2.5.5 从傅立叶级数到小波变换.

Fourier变换理论在现代分析中占有核心的地位.在课堂上我们详细讨论Fourier级数与Fourier变换的基本概念和原理，介绍小波变换，分数阶Fourier变换基本思想.对这一章，我们设置了探索类问题.

（i）通过查阅相关书籍进一步了解Fourier变换在工程领域的应用，并针对你感兴趣的领域写一份报告，并谈谈你对问题的理解与认识.

（ii）通过查阅相关书籍进一步了解小波变换的基本思想和方法以及在工程领域的应用，并针对你感兴趣的领域写一份分析报告，并谈谈你对问题的理解与进一步的设想.

（iii）通过查阅相关书籍进一步了解分数阶Fourier变换的基本思想和方法以及在工程领域的应用，并针对你感兴趣的领域写一份报告，谈谈与Fourier变换相比，分数阶Fourier变换的优势.

针对这些问题，学生成立了许多研究小组，通过查阅书籍进一步学习，学生对自己感兴趣的领域写出了分析报告，很多同学对语音识别产生了浓厚的兴趣.

2.5.6 数项级数与函数项级数.

数项级数的内容应该是数列极限问题的推广，函数项级数研究的中心就是和函数的分析性质，我们设置如下探索类问题.

（i）研究比Raabe判别法更精确的正项级数收敛的判别法.

随着m的增大，以｛bm，n｝为基数列的判别法的精度不断提高，由此得到足够高精度的正项级数判别法，结论如下：

2.5.7 与计算机相结合的探索类问题.

计算机技术的迅速发展改变了人们思维方式和科学研究方式，促进了许多数学分枝的迅速发展.因此我们淡化了函数作图和过于复杂的积分计算等问题的教学，增加了非线性方程求根的数值方法、数值积分，非线性数值优化初步以及常微分方程数值求解的基本理论问题，这些内容都依赖用计算机来实现算法和进行分析，这些内容提高了学生利用计算机解决问题的能力.

（i）研究一类高振荡常微分方程数值解法和误差分析.

（ii）研究一类二阶延迟常微分方程的数值解法，并给出误差分析.

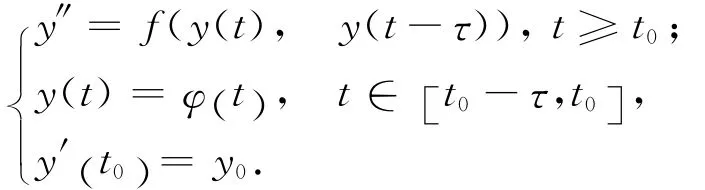
（iii）用连续函数介值定理和闭区间套定理研究下面非线性方程组根的计算方法.

（iv）利用李查逊外推（Richardson）研究广义积分的外推算法，并编程实现.研究小组对上述问题进行研究，问题（i）和（ii）的研究结论发表论文见附录5）.

3 附录：学生研究小组发表录用论文

1）王玮彬（39192109），马建华（39191221），杨小远.向量函数一致连续的比较判别方法研究［J］.数学理论与应用，2012，2（1）：45－52.

2）杨小远，范子沛（38060505），孙玉泉.《工科数学分析》中的探索类问题及教学案例［J］.高等数学研究，2012，15（1）：98－102.

3）王建元（39061422），张博宇（390614080），杨小远.二重级数收敛性研究［J］.河南科学，2011，29（12）：1387－1397.

4）孙玉泉，张文峰（39027126），杨小远.微积分中积分的统一与运算［J］.河南科学，2011，29（2）：391－396.

5）张凯（39061511），唐文琦（39061629），魏华（39061525），杨若松（39061629），杨小远.一类常微分方程数值解法［J］.河南科学，2011，29（2）：127－132.

6）杨小远，叶子豪（38060228），杨南君（38060226）.正项级数判别法的进一步研究［J］.河南科学，2010，28（5）：510－514.

7）杨小远，马建华（39191221），张立文（39191224），王玮彬（39192109）.关于函数一致连续性的判别方法研究［J］.河南科学，2010，28（6）：635－637.

8）杨小远，周渝智（39192119），林柏洪（39191121）.N阶导数的外推算法研究［J］.河南科学，2010，28（7）：762－766.

9）杨小远，王玮彬（39192109），张立文（39191224）.振荡函数一致连续性研究［J］.河南科学，2010，28（8）：899－900.

10）杨小远，王玮彬（39192109），马建华（39191221）.多元振荡函数一致连续性研究［J］.河南科学，2010，28（9）：1061－1064.

11）杨小远，林柏洪（39191121），张权（39191205）.高维李查逊外推算法的研究和应用［J］.河南科学，2010，28（10）：1213－1220.

12）杨小远，王玮彬（39192109），马建华（39191221）.多元函数一致连续的比较判别方法研究［J］.河南科学，2010，28，（12）：1501－1503.

13）张凯（39061511），唐文琦（39061629），魏华（39061525），杨若松（39061629），魏成（39061523），杨小远.关于罗尔定理的进一步讨论［J］.高等数学研究2010，13（5）：58－60.

4 结 论

本文详细介绍了我们在主讲《工科数学分析》课程中以问题驱动的研究性微积分教学模式和培养学生创新能力的尝试以及取得的成绩.我们不能说学生的研究结论有多重要，但是他们迈出可喜的一步，他们懂得了如何学习，如何思考问题，养成开放思维的习惯，为今后的学习和未来的研究打下扎实的基础.

［1］李尚志.线性代数［M］.北京：高等教育出版社，2011.

［2］国家视频精品课程［DB］.http：∥video.jingpinke.com／details？uuid＝8503ff93－1361－1000－95c1－fae62e9cd3a4.

Fostering Creativity in College Freshmen：an Empirical Exploration

YANGXiao－yuan，LIShang－zhi
（Department of Mathematics，School of Mathematics and Systems，Beihang University，Beijing 100191，China）

This paper details an innovative approach used in teaching Analysis for Engineers.The projects－based curriculum and the question－driven instruction mode provide an effective vehicle for developing students＇creativity，a significant improvement upon the traditional curriculum design.

analysis；creativity；projects－based calculus teaching

O177.2

A

1672－1454（2012）04－0013－09

2011－08－10

北京市精品课程建设项目；北京航空航天大学重点教改项目“工科数学分析开放式教学研究与实践”