一种新型的数字积分直线插补算法的研究*

郭永环 范希营 刘凤国

(江苏师范大学机电工程学院，江苏徐州 221116)

插补算法是整个数控系统控制的核心，其稳定性和算法精度将直接影响到CNC系统的性能指标。根据插补采用的原理和计算方法的不同，可有许多插补方法。目前应用的插补方法分为2类:基准脉冲插补和数据采样插补。基准脉冲插补中常用的有逐点比较法(在2个坐标轴开环的CNC系统中应用比较普遍，一般不用于多轴联动，应用范围受到一定限制)和数字积分法(简称DDA法，易于实现多坐标轴联动)。本文主要研究新型的DDA法。由于传统的DDA法沿各坐标轴脉冲频率不均匀，进给速度不够快，以及插补误差较大，精度较低。因此国内外许多学者研究了各种改进方法，取得了丰硕的成果［1－6］。这些成果中有的插补精度提高了，但由于算法复杂使得插补速度却降低了［7－9］;也有的沿x轴脉冲分配均匀，但沿y轴脉冲分配不均匀［10－11］。本文将研究一种提高精度但算法简单以及各轴脉冲分配均匀的插补算法。

1 传统的DDA法存在的不足

近年来，国内外学者取得了可喜的成绩［1－12］，但在下述3个方面还需进一步改进和提高。

(1)沿各坐标轴脉冲频率不均匀 例如，起点坐标为o(0，0)，终点坐标为A(10，7)，用传统的DDA法进行直线插补时，被积函数寄存器为四位二进制寄存器，累加器和终点计数器也为四位二进制计数器，迭代次数为24=16次时，插补结束。插补计算的过程如表1所示。

表1 传统数字积分插补法直线插补运算过程

根据表1可以看出脉冲沿x轴发出10次，沿y轴发出7次，x轴脉冲分配不均匀，y轴脉冲分配更不均匀，且间隔增大，将造成步进电动机失步，使各轴运转不平稳以及步进电动机噪声增大，影响工件的表面质量。

(2)插补精度较高时，进给速度不够快。

(3)插补算法简单时，插补误差较大，精度较低。

2 新型DDA法直线插补原理及实例

2.1 新型DDA法直线插补原理

以第一象限直线插补为例，设直线起点为o(0，0)，终点为A(xe，ye)，如图1所示。对xoy平面上的一条直线(如图1中的oA)可用下面的方程式来表达:y

将式(1)两边对x求导得，并对时间微分得:

这里，dy/dt、dx/dt的物理意义分别对应动点沿y轴和x轴方向上的运动速度分量。

又可以改写成:

式中:k为比例常数。

当xe＞ye时，只能走x或x、y同时走的方式。说明沿x轴方向的运动总步数大于沿y轴方向的总步数，所以每一次插补中都沿x轴正向进给一步。由此说明了在插补过程中不需要判断x轴在插补过程中的累加，从而只要判断y轴方向在插补过程中的累加［12］。其中脉冲当量为单位脉冲，循环次数q1为(xe，ye)中的最大数，由于xe≥ye，则对y轴方向积分［13］为

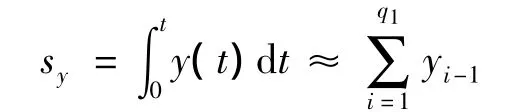
被积函数寄存器存放y轴终点坐标值ye，每来一个ΔT脉冲，被积函数寄存器里的函数值送往相应的累加器中相加一次。当累加和超过累加器的容量时，便溢出脉冲，作为驱动相应坐标轴的进给脉冲y，而余数仍存在积分累加器中。

设积分累加器控制极限为q1，当超过积分累加器控制极限q1时，必须发出脉冲溢出。若将q1规定为单位“1”(相当于一个输出脉冲)，那么积分累加器中的存数总是小于q1，即为小于1的数，该数称为积分余数。如将ye累加q1次后的y积分值［14］应为

积分值大于q1的部分表示溢出的脉冲，而余数部分存放在累加器中，即:

积分值=溢出脉冲数+余数

表2 新型DDA法直线插补的计算过程

当两个坐标轴同步插补时，用溢出脉冲控制机床的进给，就可以走出所需的直线轨迹。

若x向已走够指定步数q1=xe时，即插补结束。

为了减小插补误差，提高插补精度，可以在插补开始时设置积分初值为终点坐标值中最大值的一半［14］，即sy=xe/2。

对于x轴，不管y轴如何变化，在每次插补过程中，x轴都向正向走一步，也就是说，x轴在每次插补过程中都有脉冲输出。而y轴在某一周期可能走也可能不走，仍不能保持y轴均匀分配脉冲。因此将累加器控制极限q1分成ye等分，即每等分为q1/ye，其中累加器中y的余数为sy，也是分成ye等分，即每等分为sy/ye。当sy+ye≥q1时，为了能使y轴均匀分配脉冲，y轴应该在待定时刻发出脉冲，即和新型插补法计算的时间之间有一个时间差为［13］

其中:T为传统DDA法的脉冲发出时刻。

如果sy+ye＜q1时，就不必考虑y轴的走向。同理，当xe＜ye时，只能走 y或 x、y同时走的方式，同样可以分析xe≤ye时的插补情况。

2.2 新型DDA法直线插补计算实例

设直线的轨迹为oA，起点坐标为o(0，0)，终点坐标为A(10，7)，则脉冲个数q1=max(10，7)=10，令积分初值为sy=xe/2=10/2=5，y轴发出脉冲与产生的时间差为各个脉冲特定时刻ΔT=(q1－sy)/T/ye。其中sy为上步中积分修正值，其计算结果如表2所示。

3 新型DDA法直线插补轨迹及脉冲波形分析

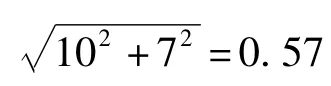
两种DDA法直线插补的脉冲分配波形如图3所示。图3a与3b相比较可以看出在数控加工过程中，传统的DDA直线插补法的各坐标轴发出脉冲的时间间隔极不均匀，而且循环次数较多，从而降低了插补速度，影响了生产率。新型的DDA直线插补法使得各坐标轴发出脉冲的时间间隔均匀，提高各轴步进电动机运行的平稳性，减少了失步的可能性。同时插补速度大大提高，由传统的DDA直线插补累加16次(如表1所示)减少到10次(如表2所示)，而进给速度并没有降低，也未影响生产率。

4 结语

(1)新型DDA直线插补算法使x、y坐标轴脉冲分配较均匀，没有周期性变化。

(2)新型积分直线插补算法简单，插补次数取终点坐标值较大者。而传统的插补算法的插补次数与寄存器的位数有关，如果寄存器的位数N=3，则要累加n=23=8，即插补8次，如果寄存器的位数N=4，则要插补16次。因此传统的插补算法当寄存器的位数越大，则插补次数越多，插补效率越低。

(3)新型DDA直线插补算法插补误差小于0.5个脉冲当量。

［1］YANG Minyang，Hong Wonpyo.Three － dimensional reference pulse linear and circular interpolators for CNC systems［J］.International Journal of Machine Tools＆ Manufacture，2001(41):555－566.

［2］Pedro L D Peres，Ivanil S Bonatti，Walter C Borelli.The linear interpolation method:A sampling theorem approach［J］.Controle y Automacao，2003，14(4):439 －444.

［3］Chen Hsinchuan，Chiang Jenshiun.A low －jitter phase－interpolation direct digital synthesizer using single capacitor integration［J］.International Journal of Electrical Engineering，2005，12(3):225 －232.

［4］Tsai，HUI Feng，JIANG Zanghao，et al.Interpolated timing recovery using raised cosine pulse［J］.International Journal of Electrical Engineering，2005，12(4):391 －398.

［5］LI Guihua，FEI Yetai，MA Xiushui.Principle of error compensation in long axle cutting［J］.Nongye Jixie Xuebao/Transactions of the Chinese Society of Agricultural Machinery，2006，37(6):131 －133.

［6］MENG Shuyun，ZHAO Dongbiao.Direct interpolation algorithm for pen－ cutting of sculptured surfaces［J］.Journal of Southeast University(English Edition)，2006，22(1):73 －77.

［7］ZHAO Qingzhi，LIU Zhengxun，GU An，et al.New machining method for different top and bottom shaped workpiece with LS－WEDM based on difference interpolation theory［J］.China Mechanical Engineering，2006，17(8):793 －797.

［8］王忠平.基于DSP的数控雕刻系统研究及其仿真实现［D］.上海:上海交通大学，2007.

［9］林砺宗，刘磊.基于TMS320F2812的多轴运动控制器研究［J］.微电机，2007，40(9):40 －48.

［10］程铁汉.在线工业标记打印机的研究［D］.重庆:重庆大学，2008.

［11］古至和.嵌入式数控雕刻机软件系统开发［D］.成都:电子科技大学，2009.

［12］杨树莲.快速数字积分插补算法及其实现.机床电器，2003(6):12－14.

［13］王广炎，张润孝，王小椿.脉冲均匀化插补方法［D］.西安:西安交通大学，2000.

［14］李郝林，方键.机床数控技术［J］.北京:机械工业出版社，2000.