基于分级聚类和近邻函数准则的目标分群算法＊

刘维国 庄锦成

（91550部队91分队 大连 116023）

1 引言

由于飞行器开机录取扇面内可能存在非预定打击编队目标以外的其它目标，因此必须进行目标编队分群，剔除非预定打击目标。根据编队目标间的距离特征进行预定打击目标编队决策，这正符合聚类算法“凡是同一类的样本其特征向量应该是互相靠近的，而不同类的样本其特征向量之间的距离要大得多”的基本特征。

动态聚类方法是一种普遍采用的方法，它具有以下三个要点：1）选定某种距离度量作为样本间的相似性度量；2）确定某个评价聚类结果质量的准则函数；3）给定某个初始分类，然后用迭代算法找出使准则函数取极值的最好聚类结果。本文主要结合分级聚类方法和近邻函数准则算法来研究目标编队分群问题。

2 分级聚类方法

任何两个样本yi和yj总会在某一水平被分为同一类，分级聚类就是这样一种划分序列。分级聚类算法的基础是两个聚类之间的相似性度量，最常用的相似性度量有最近距离、最远距离和均值距离等。在确定了相似性度量之后，就有如下的分级聚类算法：

初始时设置Γj＝yj，∀j∈I，I＝｛j｜j＝1，2，…，N｝，这里Γj是各个聚类集合，N是样本数，即初始时设每一个样本为一个类。

步骤1 在集合｛Γj｜j∈I｝中找到一对满足条件Δ（Γi，Γk）的聚类集合Γi和Γk。其中Δ（Γi，Γj）是Γi和Γk之间的相似性度量。

步骤2 把Γi并入Γk，并去掉Γi。

步骤3 把i从指标集中除掉，若I的基数等于2时，则终止计算；否则转向步骤1。

3 近邻函数准则算法的原理

对于数据集中的任何两个样本yi，yj，若yi是yj的第I个近邻，则称yj对yi的近邻系数为I。若yi是yj的第K个近邻，则称yi对yj的近邻系数为K。这里定义yi和yj之间的近邻函数值为（I＋K－2）。若用αij表示yi和yj之间的近邻函数值，则有：

3.1 规定类内损失

若在聚类的过程中，yi和yj被分在同一类，那么yi和yj是相互连接的。对于每一个这样的连接存在着一个相应的连接损失。本算法中，连接损失规定为这两个样本间的近邻函数值αij。当规定了样本间的“连接”损失后，就可以规定类内损失和类间损失。总类内损失规定为

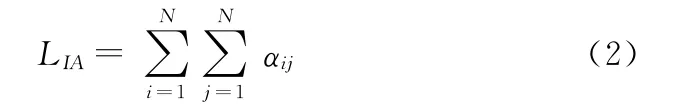
对于同一类中的yi和yj，由于存在连接关系，所以αij不等于零。对于不同类的yi和yj，由于不存在连接关系，所以αij等于零。

3.2 计算类间损失

首先计算wi和wj两类之间的最小近邻函数值γij，并取其中的最小值。则：

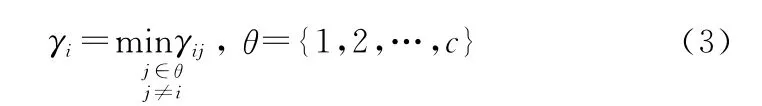
设αimax是同一类wi中两点间的最大类间损失，αkmax是同一类wk中两点间的最大连接损失。则其它类对wi类的类间损失为：

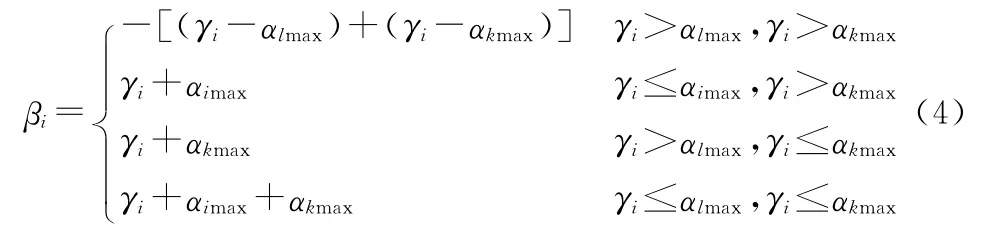
总类间损失：

式中c为类数。

对于βi，当某一类wi中的一点与其它任何一类wk中的一点的最小近邻函数值小于或等于相应的任一类内的最大“连接”损失时，就要付出一些“代价”。即βi为正值。如式（4）中的第二、三、四种情况，它意味着若当两类之间的最小近邻函数值小于或等于相应的任一类内的最大“连接”损失的话，则这两类就应当被合并。对于第一种情况，若当不同类间的最小近邻函数值大于相应的类内的最大“连接”损失的话，由于所付出的“代价”为负，则这两类就自然地为两个聚类。

4 基于分级聚类算法和近邻函数准则算法的目标编队分群算法

分级聚类算法是一种划分序列方法，这种划分序列具有如下性质：只要在K水平时样本被归入同一类后，在进行更高水平的划分时，它们也永远属于同一类。而目标编队分群仅需划分出预定打击编队即可，并不需要经过多个水平的划分把扇面内所有目标划分为一类，因此这里仅利用其选定的相似性度量来确定初始聚类，然后利用近邻函数准则算法中的类间损失来确定预定打击目标编队。其算法如下：

初始时设置录取目标数据表中的N个有效目标为N个样本，组成样本集｛y1，y2，…，yN｝，设置Γj＝yj，∀j∈I，I＝｛j｜j＝1，2，…，N｝，这里Γj是各个聚类集合，即初始时设每一个样本为一个类。

步骤1 在集合｛Γj｜j∈I｝中找到一对满足条件

的聚类集合Γi和Γk。其中Δ（Γi，Γk）是Γi和Γk之间的最近距离相似性度量。

步骤2 找出距离最近两目标之间的中心点，计算Γj中的各个样本距离该中心点的距离值，并将距离值小于2Δ（Γi，Γk）的聚类集合合并为一类，并入Γk，并从指标集I中除掉相应的样本数。

步骤3 对于指标集I中余下的类，共同形成初始聚类。对于初始聚类中的每个类i计算γi，并与αimax和αkmax进行比较。若γi小于或等于αimax和αkmax中的任何一个，则合并类i和类k，即在两类间建立“连接”。重复步骤3，直至无这样的“连接”为止。

步骤4 对于步骤3重新聚合的各类，暂取样本数最多的类即为所求的类，该类内的所有目标即为预定打击编队目标。

5 目标编队分群算法实例

5.1 求距离最近两目标中心点的坐标

经过计算可知，目标N1和N4之间的距离最近，即Δ（Γ1，Γ4）＝2000m。则目标 N1和 N4中心点 N0的方位值和距离值为（0，15000）。

5.2 形成初始聚类

计算各目标与中心点N0的距离值：N1N0＝1000，N2N0＝3100，N3N0＝2100，N4N0＝1000，N5N0＝2100，N6N0＝12369，N7N0＝13757。

因N1N0、N2N0、N3N0、N4N0、N5N0的 值 均 小 于4000m，则目标N1、N2、N3、N4、N5聚合为一类，并入Γ4，并从指标集I中除掉相应的样本数，即Γj＝｛Nj｝，j∈I，I＝｛j｜j＝4，6，7｝，形成初始聚类。

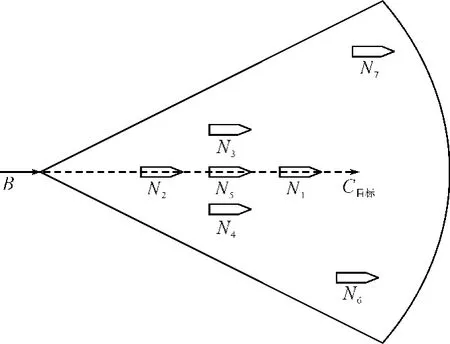
图1 非预定打击编队目标与预定打击编队目标位置示意图

5.3 在初始聚类中的任意两类间建立“连接”

对于Γ4＝｛N1、N2、N3、N4、N5｝，其类内的最大连接损失N1N5＝4200m。

因为类Γ6内仅有目标N6，其与类Γ4中的一点的最小近邻函数值N6N5＝10678m，且大于Γ4类内的最大连接损失，故类Γ7不能并入Γ4。

同样，类Γ7内仅有目标N7，其与类Γ4中的一点的最小近邻函数值N7N3＝10208m，且大于Γ4类内的最大连接损失，故类Γ6不能并入Γ4。

5.4 求出预定打击编队目标

因Γ6和Γ7均不能并入Γ4，故Γ4类内的所有目标即为预定打击目标编队，即预定打击编队目标为N1、N2、N3、N4、N5。

［1］董肇军.系统工程与运筹学［M］.北京：国防工业出版社，2003，1.

［2］张剑.军事装备系统的效能分析、优化与仿真［M］.北京：国防工业出版社，2000，1.

［3］陈玉文.海面机动目标散布规律及反舰导弹搜索区的划分［J］.飞航导弹，1999（7）.

［4］孙国祯.海军舰艇电子对抗作战使用.海军大连舰艇学院，1998.

［5］徐敏，程凤舟，陈士橹.反舰导弹多目标识别技术探讨［J］.战术导弹技术，2000（2）：35－40.

［6］李启元，段立，李亚楠.海战场目标航迹间距离聚类方法［J］.计算机与数字工程，2010，38（5）.

［7］陈玉文.海面机动目标散布规律及反舰导弹搜索区的划分［J］.飞航导弹，1999（7）：6－10.