一类新的数论函数

管训贵

（泰州师范高等专科学校 数理信息学院，江苏 泰州 225300）

1 引言及主要结论

长期以来，数论函数的性质一直是数论中一个引人关注的课题[1].2004年，A.Murthy和M.Bencze[2]引入了数论函数f（n），其定义如下：

定义 对于正整数n，如果存在正整数k可使kn+1是素数，k|( )n-1 且（n-1）/k不是合数，则设f（n）表示适合此条件的最小的k；否则f（n）=0.当f（n）=0时，n称为函数f（n）的一个零点；当f（n）=1时，n称为函数f（n）的一个单位.容易算得表1.

对此，A.Murthy和M.Bencze[2]曾提出如下猜想：

猜想1f（n）有无穷多个零点.

2011年，乐茂华[3]运用素数分布的结果证实了此猜想，不过他的证明非初等.

通过表1，我们又得到

猜想2 当且仅当p=1或p与p+2是一对孪生素数时，f（p+1）是f（n）的一个单位.本文运用初等方法证明了上述猜想，即证明了

定理1 当且仅当p=1或p与p+2是一对孪生素数时，f（p+1）=1.

定理2若素数p≡1（mod 6），则f（p+1）=0.

推论f（n）有无穷多个零点.

2 引理

引理 形如p≡1（mod 6）的素数有无穷多个.

证明 可参见文献[4].

3 定理的证明

先证定理1.

当p=1时，由表1知，f（2）=1.设p与q=p+2是一对孪生素数，n=p+1，此时适合k|( )n-1的正整数k仅有k=1和p.显然，当k=1时，kn+1=n+1=p+2=q是素数，且（n-1）/k=n-1=p不是合数，故f（p+1）=f（n）=1.

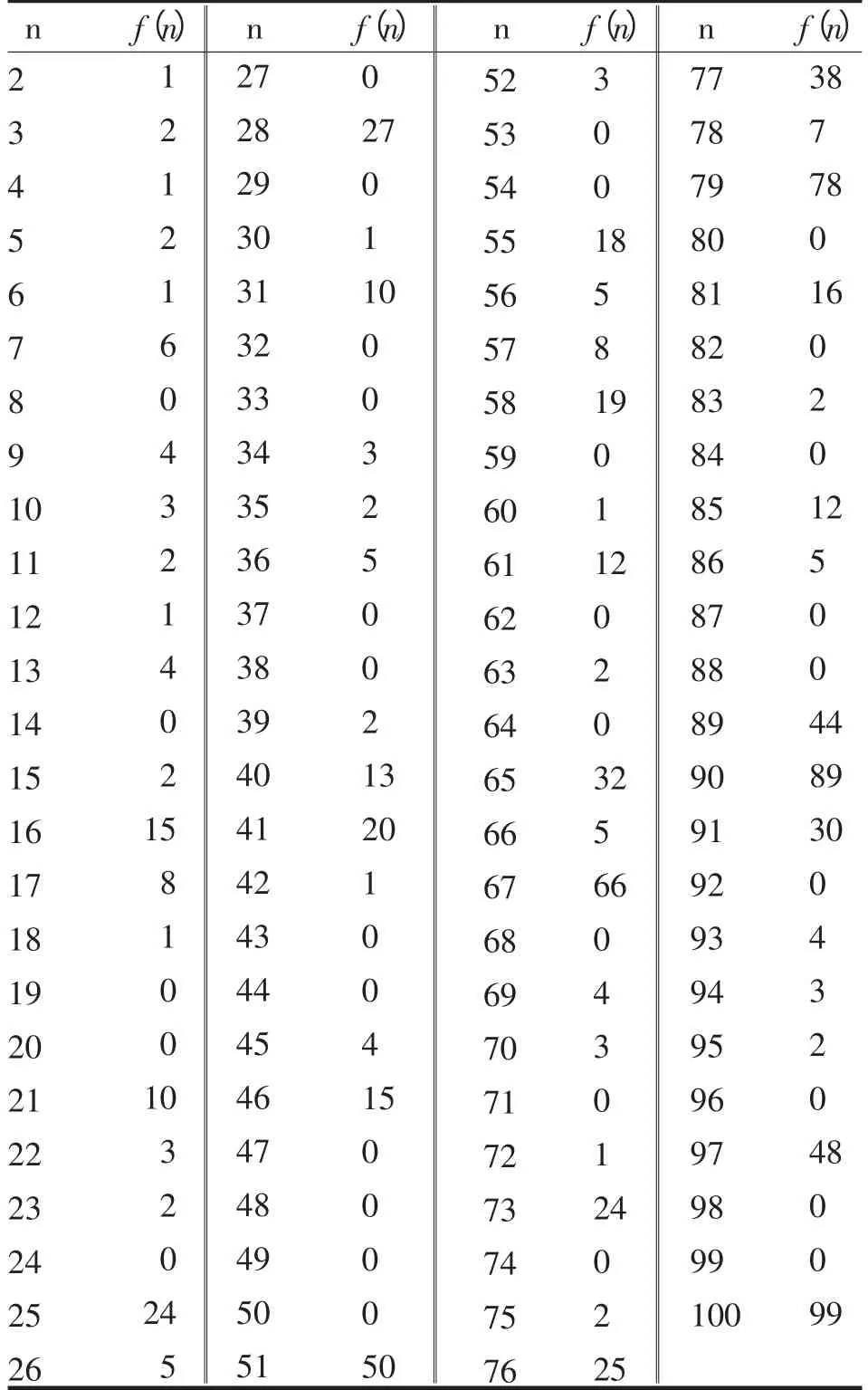
表1 不超过100的n对应的f(n)的函数值Tab.1 The function value of f(n)corresponds to n＜100

反之，设f（n）=1，则由定义知kn+1=n+1=q应为素数.又（n-1）/k=n-1不是合数，故n-1=1或p（p为素数）.此时n=2或p+1.再由n=p+1=q-1知q-p=2，故p，q是一对孪生素数.证毕.

再证定理2.

设p是奇素数，且p≡1（mod 6），n=p+1，此时适合k|( )

n-1 的正整数k仅有k=1和p.当k=1时，kn+1=n+1=p+2≡3（mod 6）不是素数；当k=p时，kn+1=p（p+1）+1≡3（mod 6）也不是素数，故f（p+1）=f（n）=0.证毕.

由引理知，形如p≡1（mod 6）的素数有无穷多个，故f（n）的零点p+1有无穷多个，推论得证.

此外，从表1还可以得出：f（n）是非积性函数.

由于f（n）是一个新的数论函数，它还有许多性质值得人们去探讨.比如

问题1当正整数n为何值时，f（n）=n-1？

问题2f（n）是否存在无穷多个单位？

问题3 当m，n满足怎样的关系时，f（m）=f（n）？

[1]Guy R K.Unsolved problemsin number theory[M].New York：Springer Verlag,1981.

[2]Murthy A,Bencze M.Open question 1520[J].Octogon Math.Mag,2004,12(2)：1009.

[3]乐茂华.一类数论函数的零点[J].湛江师范学院学报,2011,32（6）：41-42.

[4]管训贵.初等数论[M].合肥：中国科学技术大学出版社,2011：184-185.