大型整流罩分离动力学简化建模及仿真分析①

李 哲，范学领，孙 秦，万小朋

(西北工业大学航空学院，西安 710072)

0 引言

整流罩在发射任务中主要起到保护有效载荷不受气动力、气动加热及声振动等影响的作用。罩体的结构形式、连接关系及其变形对实现整流罩功能以及到达指定地点后和箭体安全分离有着决定性作用［1－4］。大型整流罩分离时，2个半壳在平动同时，将发生呼吸运动、弯曲运动和扭转运动［5－6］。这是由分离力、整流罩旋转导致的惯性力、火箭纵向和横向加速度等因素引起的典型多体动力学运动过程。同时，整流罩大型尺寸及轻而软的结构特点使得分离过程中的弹性变形不可忽略，抛罩过程是由可变形体及刚体组成的系统在大范围空间运动时的动力学行为，属于柔性多体动力学问题［7－8］。因此，进行大型整流罩分离动力学分析既要考虑结构的弹性变形，又要计入结构的空间大范围相对运动，以及弹性运动和刚体运动的耦合。

虑及大型整流罩体结构构造的复杂性及计算效率和软硬件条件限制，对抛罩动力学过程进行合理的有限元简化建模具有工程意义。本文首先研究了大型整流罩分离动力学分析相关的有限元简化建模技术，针对不同部件特点进行了多种方案设计，并验证了各方案的动力学品质特性，校验了模型简化的合理性。在合理的模型简化基础上，进一步分析了大型整流罩分离动力学行为。

1 大型整流罩分离动力学

柔性多体系统动力学研究可变形物体和刚体所组成的系统在大范围空间运动时的动力学行为，其特征是同时存在变形运动、刚体运动及其耦合特性。对于柔性体运动分析，尤其是在小变形情况下，可采用类似刚体运动分析方法，将复杂的柔性体运动分解为几种简单运动［9－11］。

柔性多体系统运动学方程为

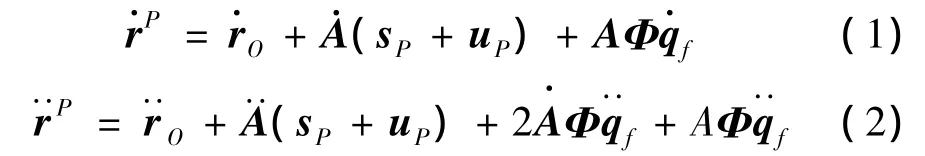
式中 r为柔性体上P点在惯性坐标系中的向量;rO为浮动坐标系原点在惯性坐标系中的向量;A为浮动坐标系和惯性参考系之间的坐标变换矩阵;sP为变形前P点在浮动坐标系中的向量;uP为P点的相对变形向量;Φ为满足里兹基向量要求的假定变形模态矩阵;qf为相应的广义坐标。

柔性多体系统运动微分方程可在拉格朗日方程的基础上导出［9－10］:

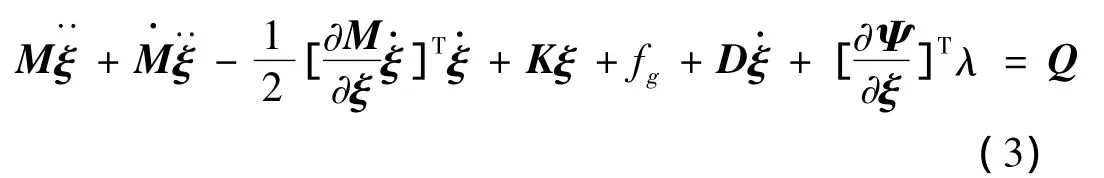
式中 Ψ为约束方程;λ为拉氏乘子;ξ为广义坐标;Q为投影到广义坐标ξ上的广义力;M、分别为柔性体的质量矩阵及其对时间的导数;∂M/∂ξ为质量矩阵对柔性体广义坐标的偏导数。

2 大型整流罩简化建模技术

所研究整流罩罩体为回转体结构构型(图1)。沿纵向对称面分左右两瓣，最大高度9.56 m，最大结构质量590 kg。半罩结构体由端头帽、前锥段、圆柱段及倒锥段4个部段通过机械紧固件连接而成。

2.1 夹层结构等效简化

对于冯卡门锥段和前柱段的夹层结构，可将其等效简化为正交各向异性均匀板。由于夹层结构的面板刚度和密度远大于夹芯材料，因此有必要对该简化方式进行有效性验证。

建立半径R=2.5 m的半圆柱面，假设柱面由3层构成，各层均为各向同性材料且厚度、密度以及刚度比和实际整流罩夹芯结构相近。E11=E22=2.02×109;ν12=0.25;G12=1.61 ×108;G13=1.39 ×108;G23=9.18×107。对柱面分别采用如下3种方案来进行分析。

方案1:面板为壳单元，夹芯为体单元。

方案2:整个夹层结构为3层铺成的层合板，并将其定义为壳单元。

方案3:整个夹层结构等效为一均质板，并将其定义为壳单元。

对采用以上方案所建的有限元模型分别进行模态分析，所得频率如表1所示。

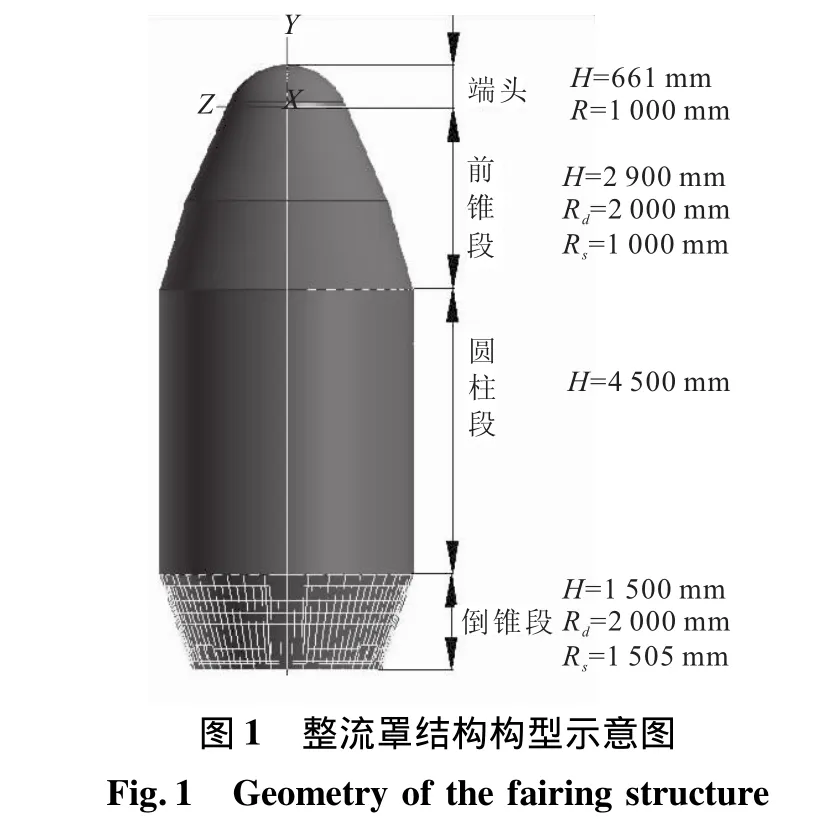
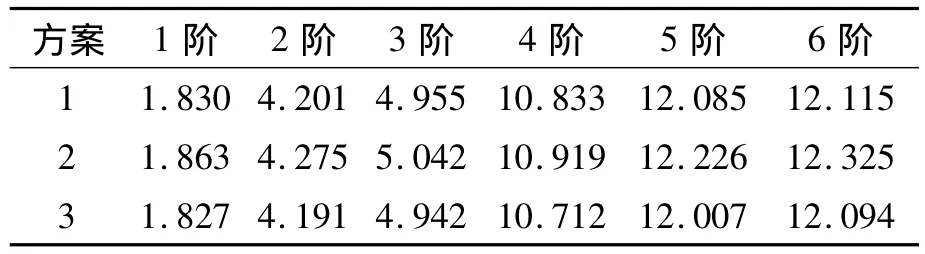
表1 不同工况对应的频率(夹层结构)Table 1 Natural frequencies for different cases Hz

由表1可知，3种方案对应的同阶频率最大相对误差为2.02%，因此可认为以上3种不同的建模方案对结构的动力学特性影响不大，将夹层结构简化为匀质板进行模型简化是行之有效的。

2.2 参考面位置设置简化

整流罩不同的部段有着不同的厚度，因而各部段的中面离整流罩中心轴的距离也不一样。为了简化建模，假设各部段的中面均与整流罩的外表面重合。通过下述算例分析中面位置移动可能带来的误差。

建立2个半圆柱面，一个半径R=2.48 m，另一个半径R=2.5 m。假设2个圆柱面的材料都是铝合金，且厚度都为0.01 m。对2个半圆柱面采用壳单元建模并在无约束条件下分别进行模态分析，其频率结果如表2所示。由表2可知，半径分别为2.48 m和2.5 m模型的各阶频率相对误差都不超过1.6%，因此可认为2个模型的动力学特性没有明显差别。由于整流罩夹层结构的比刚度较铝还要大，若将各部段的中面层简化到整流罩的表层，其对结构的动力学特性影响仍会小于1.6%。

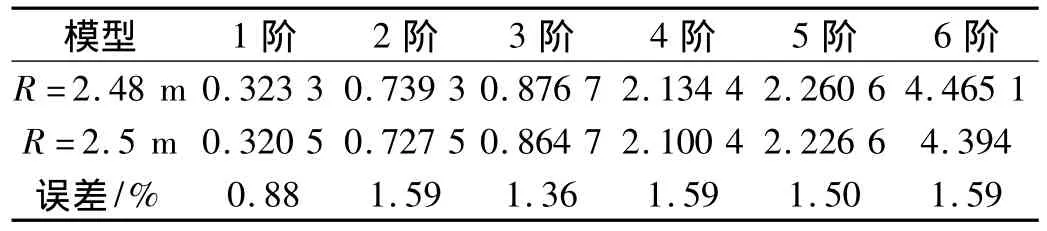
表2 不同工况下的低阶固有频率(参考面位置)Table 2 Natural frequencies for different cases Hz

2.3 环形框的简化

整流罩的环形框起着维持结构基本外形的作用，因而对结构的动力学特性有着较大影响。考虑到环形框相对于罩主体结构有着较大的密度与刚度，在对环形框进行简化建模前有必要了解其刚度与质量的不同(采用梁单元建模时，即梁单元的型心与质心是否偏移所造成的刚度与质量分布的不同)对结构动力学特性的影响。建立一半圆柱面，在柱面的2个端头以及中间位置各设置一个环形框。柱面以及框横截面的几何及材料均依照整流罩前柱段的数据给出。对柱面结构分以下几种工况进行模态分析:

工况1:型心和质心都不偏移;

工况2:型心偏移，质心不偏移;

工况3:型心不偏移，质量为0;

工况4:型心偏移，质量为0;

工况5:型心和质心都偏移。

所谓的“不偏移”指环形框对应的梁单元的型心或者质心位于柱面上;“偏移”则是指环形框对应的梁单元的型心或质心按照环形框的实际位置向内偏离柱面，其偏移量为框截面实际型心离整流罩外表面的距离。各工况下均不对模型进行约束，模态分析所得低阶频率如表3所示。

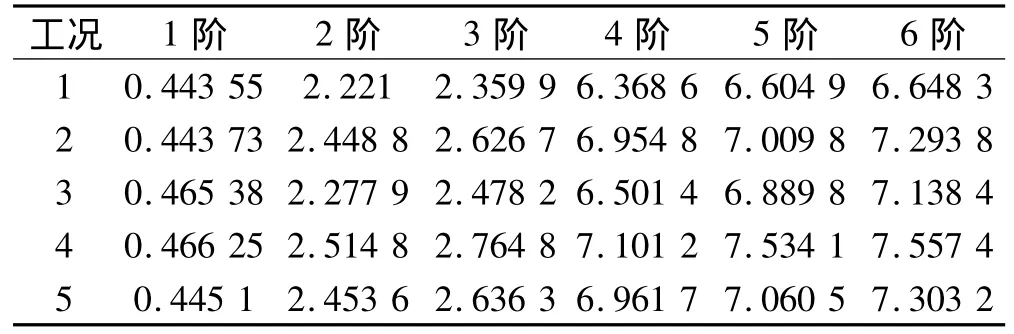
表3 不同工况下的低阶固有频率(环形框)Table 3 Natural frequencies for different cases Hz

由表3可知:

(1)环形框对应的梁单元的型心位置，即环形框的刚度对结构的动力学特性影响较大，不偏移梁单元型心引起的频率最大相对误差达到11.3%。

(2)环形框的质量对结构的动力学特性影响较大，忽略环向框的质量造成的频率最大相对误差达到7.37%。

(3)环形框对应的梁单元的质心分布对结构的动力学特性影响较小，质心不偏移造成的频率相对误差仅为 0.72%。

由于DYTRAN软件的梁单元不具备直接设置偏移量的技术功能，本文采用平行移轴的等效惯性矩处理方式进行简化。这种简化方式实质上属于前面验证工作中的工况2，即“型心偏移，质心不偏移”，表3结果表明其误差不超过1%。因此，可认为该处理方案并不会对结构的动力学特性产生较大影响。

2.4 弹簧支架角盒的简化

为将弹簧支架的“簸箕”型角盒合理简化为梁架结构，其简化原则如下:

(1)靠近半罩周向的弹簧支座两侧端面，质量的大小、分布势必对结构的动力学特性有着较大的影响，因此简化前后结构的质量大小、分布应基本一致。

(2)弹簧支座主要起的是向半柱环、桁条、支撑框传递弹簧推力的作用，因此简化前后结构传递弹簧力的效果应该大致相同。

(3)由于结构所受到的载荷时间历程和弹簧力的加力点的位移直接相关，因此弹簧力作用点处的刚度，特别是沿整流罩纵向的刚度应该得到保证。

(4)弹簧支座下端面使得支座所在的罩的区域周向刚度得到加强，因此简化后的结构环向刚度应该得到保证。

2.5 大型整流罩有限元模型

采用上述典型结构形式的有限元建模方式，所研究整流罩结构有限元模型如图2所示。

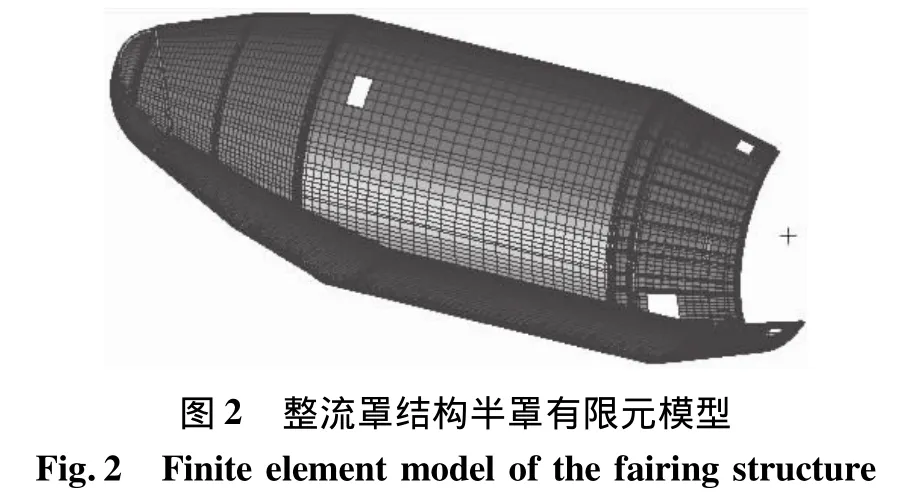
图2中，端头帽弓形框、加强框、支撑梁、底端框采用BEAM梁单元;底框对接边以及底框侧壁与端头帽壳相叠部位采用QUAD4板壳元;端头帽本体其他部位采用TRIA3及QUAD4板壳元。

对前锥段壳体进行网格划分采用QUAD4板壳元，而其他框则采用BEAM梁单元进行网格划分。

前柱段本体有限元网格划分采用QUAD4型三夹层板壳单元，其他框则采用BEAM梁单元进行网格划分。

倒锥段壳体采用QUAD4、TRI3壳单元，而对其他所有框、加强筋与桁条均采用BEAM梁单元;弹簧支座的“簸箕”型角盒被简化为BEAM梁单元进行处理;后柱段外表面底端两处的罩体铰支梁采用BEAM梁单元处理。倒锥段网格加筋壁板对应的网格内的面板属性定义为各向同性壳，加筋条定义为梁单元。弹簧支架角盒简化成梁架结构。

3 数值结果

3.1 半罩分离运动特征量

对整流罩结构分离面约束状态下阶跃式释放罩体边界位移约束，按特征量计算方法，获得整流罩(半罩)结构分离运动特征量，计算结果见表4。

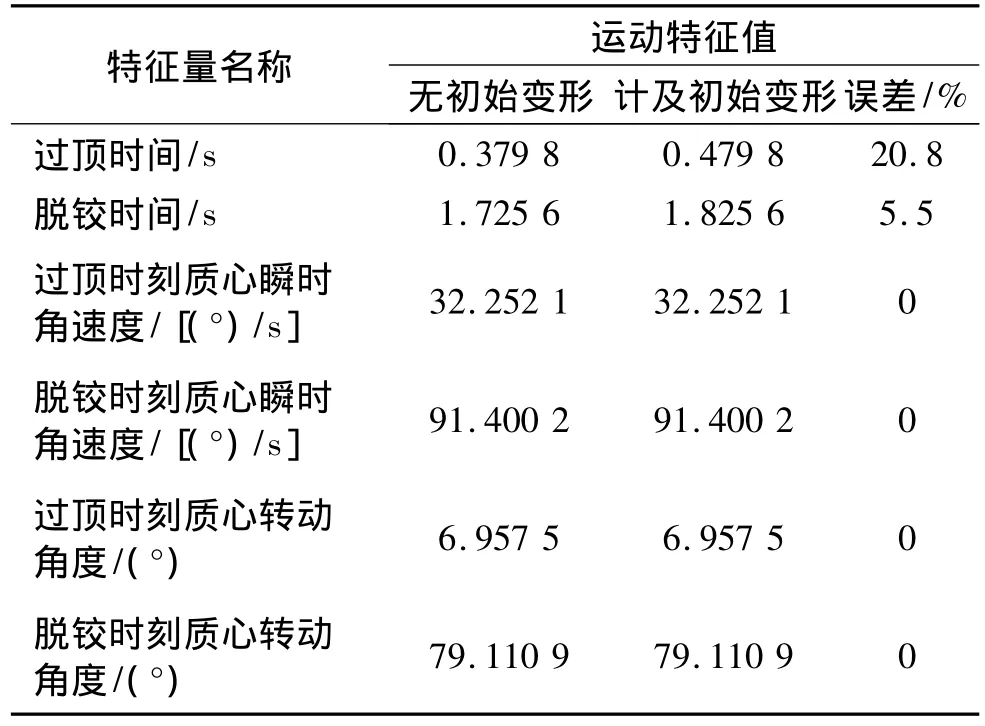
表4 罩体结构分离运动特征量Table 4 Characteristic parameters of separation

对比表4中是否计及初始弹性变形的计算结果可知，除过顶时间外，解锁前结构体内能状态对半罩体分离运动的基本特征量影响不显著，尤其是两种情况下的脱铰时刻质心瞬时角速度和质心转动角度均相差很小。因而在对大型整流罩分离过程进行数值模拟时，基于计算效率及软硬件条件限制，可忽略分离面解锁前因弹簧作用导致的整流罩初始装配弹性变形对抛罩动力学行为的影响［3－4］。

3.2 分离角速度及位置变化历程

取铰链转动点为坐标原点，将原来的总体坐标系平移到铰链点，建立新的转动坐标系。在铰支点坐标系中质心到铰点距离的变化时间历程曲线如图3所示。

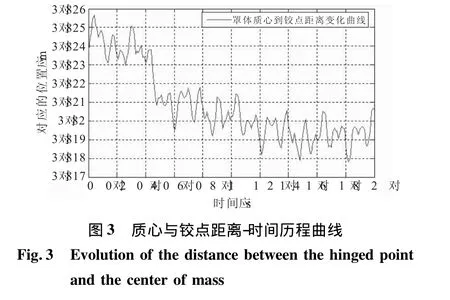
3.3 罩内可用包络空间损失

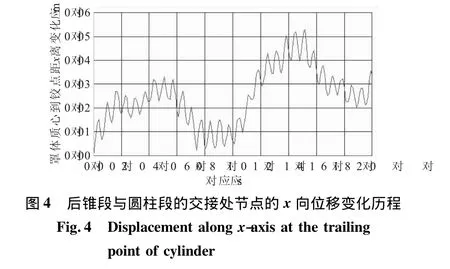
整流罩分离过程中结构x向弹性振动(即“呼吸运动”)导致罩内有效载荷可用包络空间损失，纵向分离面附近结构弹性振动幅度最大。通过对纵向分离面特定节点x向位移的分析，可获得弹性振动对可用包络造成损失的定量描述。

图4所示为整流罩分离过程中后锥段与圆柱段交接处节点的x向位移随时间变化曲线。从罩体结构弹性变形曲线可看出，最大的变形量为6 cm，满足罩体结构的安全包络空间的要求。

3.4 铰链力变化历程

图5为铰支点处x方向的约束反力随时间变化历程曲线。由图5可知，铰支点处x方向的约束反力在质心过顶前为正;过顶之后约束反力为负，其均值在－20 kN左右振动，振动幅值约为10 kN。

3.5 整流罩分离运动过程

由于整流罩初始弹性变形对抛罩动力学影响较小，可忽略不计，因而这里仅给出未考虑初始弹性变形的整流罩分离过程中的运动及变形特点，如图6所示。

整流罩分离运动过程表明，在抛罩起始阶段，整流罩有明显的弹性变形，即“呼吸运动”，从而导致罩体内部可用包络空间的减小，对整流罩下端和柱段与锥段对接部分影响明显。整流罩分离过程中柱段角点处沿径向向内位移最大，该点在火箭飞行过程中最容易对有效载荷造成危害［2］。

4 结论

(1)文中对大型薄壁整流罩结构的简化建模方法合理可行，可作为整流罩模型简化基本依据。

(2)分离面解锁前因弹簧作用导致的整流罩初始装配弹性变形对抛罩过程中质心运动、罩内可用空间包络及铰链力的影响较小，可忽略不计。

(3)整流罩分离过程中的“呼吸运动”所引起的罩内可用包络空间损失以柱段角点处最为严重(距离约为6 cm)，而越靠近罩体顶端影响越小。

［1］Ramamurti V，Rajarajan S，Rao G V.Elastic response of a typical CFRP payload fairing due to separation impulse［J］.Composite Structures，1999，45:147－154.

［2］马忠辉.大型弹性整流罩分离特点分析［J］.中国科学E辑，2009，39(3):482－489.

［3］张永杰，孙秦.整体式头罩分离运动轨迹可靠性分析［J］.弹箭与制导学报，2011，31(1):19－22.

［4］范庆志，孙秦.飞行器头罩分离技术及设计方案分析研究［J］.机械设计与制造，2008(9):8－10.

［5］Jeyakumar D，Biswas K K，Rao B N.Stage separation dynamic analysis of upper stage of a multistage launch vehicle using retro rockets［J］.Mathematical and Computer Modelling，2005，41:849－866.

［6］Cheng S C.Payload fairing separation dynamics［J］.Journal of Spacecraft and Rockets，1999，36(4):511－515.

［7］Shabana A A.Flexible multibody dynamics review of past and recent developments［J］.Multibody System Dynamics，1997，1:189－222.

［8］Huston R L.Computer methods in flexible multibody dynamics［J］.International Journal for Numerical Methods in Engineering，1991，32(8):1657－1668.

［9］陈立平，张云清，等.机械系统动力学分析及ADAMS应用教程［M］.北京:清华大学出版社，2005.

［10］陆佑方.柔性多体系统动力学［M］.北京:高等教育出版社，1996.

［11］洪振嘉.计算多体系统动力学［M］.北京:高等教育出版社，1999.