新型宽速域高超声速飞行器气动特性研究①

李世斌，罗世彬，黄 伟，柳 军，金 亮

(国防科学技术大学高超声速冲压发动机技术重点实验室，长沙 410073)

0 引言

Nonweiler于1959年率先提出了乘波构型的概念［1］，引起了世界各航天科学家的兴趣。进入21世纪，乘波构型飞行器的研究达到了空前的高度，关于乘波飞行器的研究逐渐进入实用化。2010年5月26日，X-51A的第一次试飞成功，加速了乘波构型的研究。乘波构型飞行器已经成为高超声速飞行器研究的主流，也是解决高超声速飞行难题的有效途径之一。

国内外关于乘波体飞行器开展了大量的研究工作。陈小庆、崔凯和 Huang等［2－4］在单马赫数条件，进行了乘波体的构型设计与性能研究，并根据不同的优化目标得到了相应的最优构型。Starkey、耿永兵和何烈堂等［5－9］分别在不同马赫数条件下，对不同乘波体飞行器的气动性能进行了系统研究，并考虑了不同外形在其非设计工况下的气动性能，在乘波体构型研究中取得了丰硕的研究成果，但其设计理念的根本是针对单马赫数条件下的特定流场，而这种针对某一特定的乘波体构型，不能够实现宽速域均具有良好气动特性的目标。类似这方面在单马赫数下乘波飞行器气动性能的研究很多，但针对以宽速域飞行器为目标的设计研究才刚起步，国内只有王发民等［10］对宽速域乘波布局飞行器进行了研究，亟急待深入探索。

以单马赫数设计的乘波体，在非设计状态下的气动性能变化明显，因而宽速域飞行器所要解决的是，乘波飞行器在更宽的速域范围内均具有良好的气动性能，使其在宽速域范围内的总体性能最优。要实现此目标，不仅要考虑气动力/热、结构等多种学科，还要考虑各个学科之间的耦合因素。本文仅针对宽速域乘波飞行器的气动特性进行了较深入的研究，提出了新的设计方案。

1 乘波体设计理论

在高超声速锥形流中，气流在激波上转折角小于圆锥半锥角，过了激波气流的指向还要继续转变，逐渐趋向于与圆锥母线平行。锥形流激波前后的流场关系可用Taylor-Maccoll方程［11］的无量纲形式表示:

在常规乘波体生成方法中，通过数值积分以上公式，可获得锥形流内的流线分布。本文对乘波体生成方法进行了简化，如图1所示。假设气流在激波上转折角与圆锥半锥角相同，即圆锥激波内的流线与圆锥母线平行，则可由解析方法获得锥形流内的流线分布。

定义自由来流马赫数、圆锥激波半锥角、圆锥底面半径以及乘波体机身下表面的后缘曲线形状，就可根据流线追踪的方法获得乘波体下表面前缘曲线，之后将前缘线向底面投影，完成整个乘波体机身的设计。

2 计算模型

由于乘波构型随激波角的变化曲线不大［10］，在12°激波角条件下的性能较好，故本文采用的激波半锥角β=12°，圆锥底面半径R=1 200 mm。首先分别针对Ma=4和Ma=8进行了乘波体的气动外形设计，设计参数如表1所列，进而将两者进行“串联”拼接，设计了一类新型的高超声速飞行器，如图2所示。

表1 基准(JZ)乘波体构型的设计参数Table 1 Parameters of the benchmark waverider configuration

表1 中，a= －0.5，b=0.5，c=1;JZ-1 与 JZ-2 与圆锥底面的交点相同，圆锥底面圆心与JZ-2后缘线圆心之间的距离d=790 mm。

新型乘波构型的设计参数如表2中所列，其中L为连接段的长度，H为连接段的宽度。将JZ-1进行全尺度缩比作为其前体，并取JZ-2全长的43%作为其后体，使前体后端面和后体前端面的宽度相同，然后将其进行点对点放样产生连接段，如图2所示。取最大迎风面的后端面面积作为参考面积，即与JZ-2的参考面积相同。

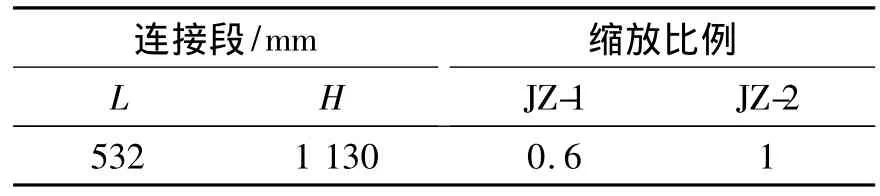
表2 “串联”乘波构型(CL)的设计参数Table 2 Parameters of the combined waverider

3 计算方法

采用三维隐式RANS方程和RNG k-ε湍流模型对新型宽速域高超声速飞行器气动性能进行数值仿真，可压缩气体的湍流方程可在适当的参考系下进行描述［12］。

式中 ρ、ui、p、τij、Fbi、Q、Cμ分别为密度、组分速度、压强、湍流剪切应力、质量组分力、主体供热和涡流粘度;Gk、YM和S分别指由速度梯度引起的湍动能量、在可压缩湍流中膨胀-耗散提供的能量和平均应变张量系数;αk和αε分别指在k和ε方程中的普朗特数;模型常数 Clε=1.42，C2ε=1.68 可由经验公式得到。

粘性系数和热导率均由质量平均混合法则，采用无滑移和绝热的壁面条件，计算域的外场条件为压强远场［13］。

由于几何模型具有对称性，故数值模拟时只需采用一半的流场来进行模拟;壁面函数采用近壁面流动模型，气体为热理想气体。

收敛标准:当残差曲线下降到10－3量级且流通量降为0.001量级时，可认为计算收敛;计算网格在机身壁面处进行加密处理;参考面积均取各模型的后端面，表3为计算模型及各模型的参考面积。

初始条件:以H=25 km、Ma=6时的状态大气参数为基准，pe=2 511.01 Pa、Te=221.65 K，采用等动压设计方法，设计范围为 Ma=4～12，动压 p=64 240.97 Pa。

表3 计算模型及参考面积Table 3 Computational model and reference areas

采用本文的数值方法，对高超声速细长体飞行器流场进行了数值模拟，获得的升阻比和俯仰力矩系数结果与实验数据吻合较好，参见文献［12］，表明本文所采用的数值方法可用于高超声速飞行器流场的模拟。

4 结果与分析

由升力系数和阻力系数计算公式，可得不同模型的CL、CD及升阻比L/D随马赫数的变化规律，如图3所示。

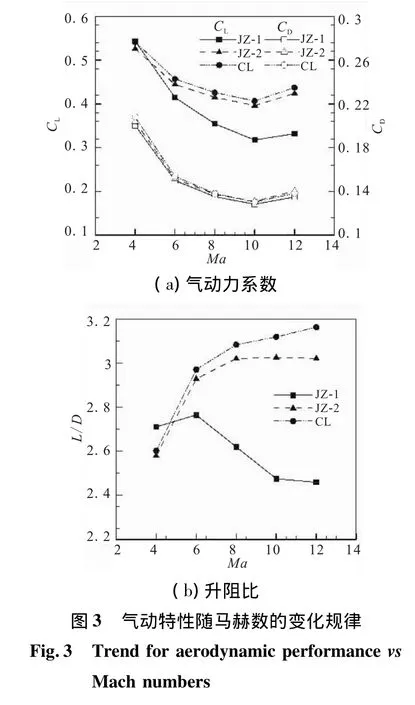
由图3(a)可知，随着马赫数增加，基准模型和“串联”模型的气动力系数先急剧降低后增加;JZ-1的升力系数降低幅度较大，“串联”乘波体的升力系数高于基准乘波体;而“串联”模型的阻力系数和基准模型的阻力系数几乎保持一致;说明连接段使“串联”乘波体的升力系数特性改进，进而提高其升阻比，改善其气动性能。

由图3(b)可知，JZ-1的升阻比先增加后降低，马赫数在6～10时升阻比呈线性急剧降低，JZ-1的气动性能随马赫数的变化较大，说明外形太薄的飞行器气动性能不稳定;JZ-2的升阻比随马赫数的增加先升高后几乎保持不变，“串联”乘波体的升阻比随马赫数的增加不断升高;当Ma＞8时，“串联”乘波体的升阻比变化不明显。在Ma=4时，“串联”乘波体的升阻比高于JZ-2却低于JZ-1，而在高马赫数下，其升阻比始终高于其他模型，说明“串联”组合乘波飞行器的气动性能，在合适的飞行马赫数条件下能够使气动性能达到最优。在设计范围内，“串联”乘波体的升阻比最大接近3.2，高于基准模型;而目标Ma=6时，并不能取得最大的升阻比，“串联”乘波体的升阻比接近3.0;“串联”乘波体的升阻比随马赫数增加而变大，而JZ-1的升阻比在Ma＞6的情况下，随马赫数升高而降低，说明JZ-1乘波体对新型宽速域乘波体的影响不明显，JZ-2乘波体在整体气动性能中起主要作用;连接段改善了“串联”乘波体的性能，说明两者适当的组合可达到“串联1+1＞2”的效果。

图4所示为Ma=8、0°攻角飞行状态下的等值线分布云图。高压区主要集中在下表面，乘波特性较好。从图4可见，由于锥导乘波的设计是根据无粘流场特性生成的，故在乘波体边缘存在部分高压向上表面溢流的现象。

图5所示为Ma=8、0°攻角飞行状态下，对称面上连接段处静压的等值线图。

结合图4和图5可知，高压区几乎全部在机体的下表面，连接段适当的坡度可提高“串联”乘波体的升力特性;而在连接段上表面处存在一定的压强，这将导致阻力的增加，适当的改善连接段的外形将能够降低乘波体飞行器的阻力性能，改善乘波体的整体气动性能。

在设计目标Ma=6下，数值模拟了攻角对气动特性的影响，图6为气动特性随攻角的变化规律。

由图6(a)可知，升力系数随攻角的增加成线性增加，阻力系数随攻角的增加而增大，且增大幅度越来越大;JZ-1的升力系数和阻力系数增加更快，“串联”乘波体的气动力系数随攻角变化趋势与JZ-2基本一致。由图6(b)可知，升阻比随攻角先增加后降低，“串联”乘波体和JZ-2升阻比的变化趋势相似，在3°攻角时升阻比达到最大;JZ-1的最大升阻比达到4.714，“串联”乘波体的升阻比在3°攻角条件下达到3.48，而且其升阻比在正攻角条件下始终处于JZ-1和JZ-2之间;在正攻角飞行状态下，JZ-1的升阻比明显高于JZ-2的升阻比，故JZ-1可作为“串联”乘波体的一部分来提高其升阻比。

由文献［14］可知，当 ∂Mz/∂α ＜0时，飞行器具有纵向静稳定性。由图6(c)可知，在－2°～10°攻角范围内，俯仰力矩系数随攻角增加单调递减，故而飞行器具有静稳定性，这是由于CM的参考点位于飞行器的50%处，使压心位于质心之后的缘故，使飞行器产生低头力矩。

5 结论

(1)“串联”方式的新型乘波飞行器的气动性能在宽速域范围内比单马赫数条件下的乘波飞行器的气动性能更优;选择合适的连接段可使飞行器的气动性能较优，达到“串联1+1＞2”的效果。

(2)“串联”乘波体的升阻比随马赫数的增加而变大，当Ma＞8时，其气动特性变化不明显，最大升阻比接近3.2，在设计马赫数范围内，升阻比不低于2.6。

(3)“串联”乘波体的升阻比随攻角的增加先增加后减小，在3°攻角时升阻比最大。在Ma=6下，JZ-1的最大升阻比为4.714，“串联”乘波体的最大升阻比达到3.48;在正攻角飞行状态下，JZ-1的升阻比明显高于JZ-2，故可作为“串联”乘波体的一部分用来提高其气动特性。

［1］Nonweiler T R F.Aerodynamic problems of manned space vehicles［J］.Journal of the Royal Aeronautical Society，1959，63:521-528.

［2］Huang Wei，Ma Lin，Wang Zhen-guo，et al.A parametric study on the aerodynamic characteristics of a hypersonic waverider vehicle［J］.Acta Astronautica，2011，69:135-140.

［3］陈小庆.高速乘波飞行器气动布局设计研究［D］.长沙:国防科技大学，2006.

［4］崔凯，杨国伟.6马赫锥体流场对乘波体性能的影响及规律［J］.科学通报，2006，51(24):2830-2837.

［5］Mazhul I I，D R R.Hypersonic power-law shaped waveriders in off-design regimes［J］.Journal of Aircraft，2004，41(4):839-845.

［6］Starkey R P，J LM.Analytical off-design lift-to-drag-ratio analysis for hypersonic waveriders［J］.Journal of Spacecraft and Rockets，2000，37(5):684-692.

［7］耿永兵，刘宏，姚文秀，等.锥形流乘波体优化设计研究［J］.航空学报，2006，27(1):23-29.

［8］何烈堂，周伯昭，陈磊.基于乘波构型的跨大气层飞行器气动布局［J］.国防科技大学学报，2007，29(4):17-21.

［9］刘济民，侯志强，宋贵宝，等.前缘钝化对乘波体非设计点性能影响分析［J］.飞行力学，2011，29(1):21-25.

［10］王发民，丁海河，雷麦芳.乘波布局飞行器宽速域气动特性与研究［J］.中国科学 E辑:技术科学，2009，39(11):1828-1835.

［11］左克罗，霍夫曼(美).气体动力学［M］:国防工业出版社，1989.

［12］Huang Wei，Li Shi-Bin，Liu Jun，Wang Zhen-Guo.Investigation on high angle of attack characteristics of hypersonic space vehicle［J］.Science China Technological Sciences，2012，55(5):1437-1442.

［13］李世斌，罗世彬，黄伟，等.新型高超声速飞行器气动构型设计［J］.弹箭与制导学报，2012(录用待刊).

［14］黄伟，柳军，罗世彬，等.尾喷管构型对高超音速飞行器纵向静稳定性的影响［J］.固体火箭技术，2008，31(4):310-312.