高超声速飞行器级间分离偏差干扰仿真①
贾如岩,江振宇,张为华
(国防科学技术大学航天与材料工程学院,长沙 410073)
0 引言
大气层内高超声速飞行器级间分离相比运载火箭或导弹级间分离更具风险性。高动压的飞行环境与分离区域的复杂流场使微小偏差可能对姿态运动产生较大干扰,按照无偏差设计状态进行分离运动计算无法预示真实飞行中的分离过程。为了评估分离系统工作性能、预估分离过程风险,有必要对偏差随机耦合干扰下的级间分离过程进行仿真分析。
高超声速飞行器级间分离动力学模型复杂、偏差因素多、耦合强烈,分离过程仿真分析难以充分预示风险、难以得到可靠结论。在美国高超声速验证项目Hyper-X中,蒙特卡洛方法被应用于助推分离过程的风险评估、分离后验证机起控策略选择、分离过程偏差灵敏度分析及验证机的六自由度飞行弹道仿真中,并通过真实飞行数据进行了仿真工具验证与不确定性参数修正。从预先仿真结果与飞行数据对比来看,蒙特卡洛方法在预测分离运动范围、预示分离过程风险等方面均取得了较好效果。文献[1-5]介绍了这些工作的进展与成果,但缺少对仿真模型与具体方法的描述。
本文以大气层内高超声速条件下串联式级间分离过程为对象,研究利用蒙特卡洛方法对这一过程进行预示的途径,建立能够支持偏差耦合仿真的分离动力学模型与分离运动特征值计算模型,建立利用蒙特卡洛方法进行分离过程仿真的具体流程。
1 分离过程主要偏差及影响
偏差的不确定性及干扰的耦合作用是高超声速飞行器级间分离过程难以准确预示的根本原因。高动压来流对微小干扰的倍增作用使分离过程对随机偏差更加敏感。影响分离过程的主要随机偏差如下:
(1)分离条件偏差(高度、速度、初始攻角、侧滑角、姿态角、姿态角速率)。高度与速度偏差直接造成动压的偏差;分离初始攻角与侧滑角偏差会引发复杂的级间流场与两级不稳定的受力环境,是分离过程必须严格控制的偏差;姿态角速率偏差会造成两级解锁后发生横向的相对偏移。
(2)弹体质量特性偏差(质量、转动惯量、惯量积、质心位置)。惯量积会引起分离后两级的动态不平衡;质心位置的横向偏移会使基于对称弹体的作用力对质心产生一个附加干扰力矩。
(3)气动特性偏差(气动系数)。分离过程流场变化十分复杂,气动系数是相对位置与相对姿态的高维非线性函数,分离过程仿真需要的气动系数很难准确得到,具有较高的不确定性。
(4)分离装置特性偏差(作用力大小、作用力的偏斜、作用点横移)。作用力的偏斜与作用点横移产生的干扰力与力矩虽然作用时间很短,但其有可能在两级近距离时导致相对横移或偏斜,造成级间区域流场的剧烈变化。
(5)推力特性偏差(推力大小、推力线偏斜与横移)。前体点火时推力上升段与后体关机的后效推力均有明显的不确定性,而推力偏差直接影响分离体轴向加速度的变化。
2 蒙特卡洛方法
蒙特卡洛方法是一类通过随机变量的统计试验或随机模拟,求解数学、物理和工程技术问题近似解的数值方法。蒙特卡洛方法可通过对系统输入偏差在一定范围内进行多次随机抽样组合,获得输出样本的统计特性,并发现可能造成系统输出超出预期临界的偏差组合[6]。
利用蒙特卡洛方法进行级间分离过程仿真的基本步骤:
(1)建立比较精确的分离过程数学模型;
(2)确定分离过程中各种偏差因素的随机分布规律;
(3)根据随机分布构造相应的数学模型,以产生各随机偏差的抽样值;
(4)将随机变量的抽样值送入数学模型,进行多次仿真,即可获得分离运动过程的子样;
(5)对多次仿真结果进行统计分析。
利用蒙特卡洛方法进行分离过程仿真详细流程如图1所示。图1中以是否发生碰撞作为分离失败的唯一判据,但在实际情况中仍有许多约束因素必须考虑。上面级运动状态是否超出了稳定飞行的范围,分离后上面级控制系统是否达到了能力极限,分离结束后上面级是否超出了要求的飞行状态等,这些都是在仿真中必须进行判断并且记录引发这些极限情况的输入参数。
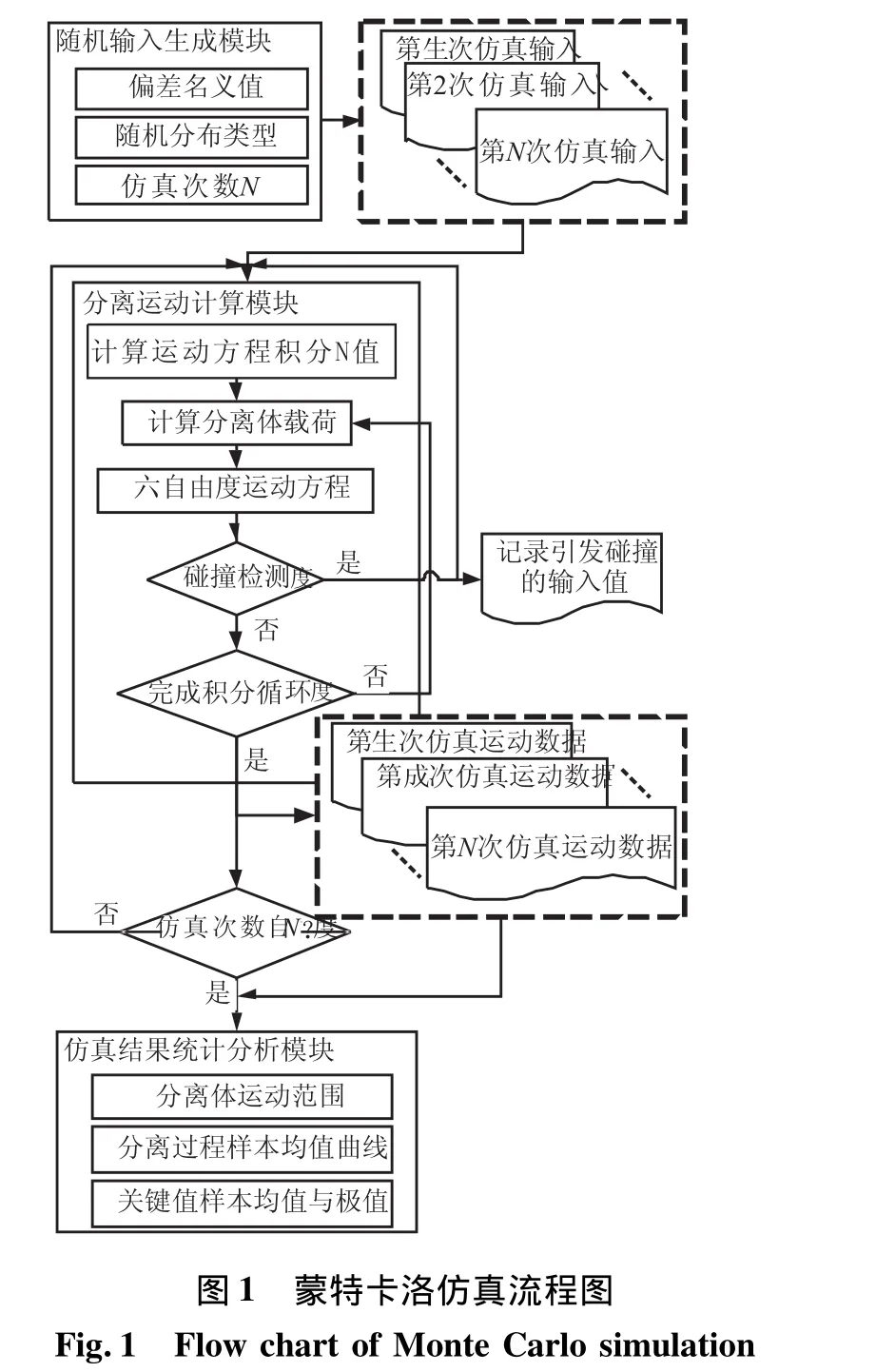
3 级间分离动力学模型
3.1 级间分离动力学运动学微分方程组
分离过程动力学模型包含2种坐标系:分离惯性参考系与分离初始时刻飞行器组合体的弹体坐标系重合;两级弹体坐标系X轴均与各自弹体轴线重合,坐标原点与各自理论质心重合。下文中坐标系转换矩阵用A表示,下标c代表惯性系,u代表上面级弹体系,d代表下面级弹体系。
两级分离过程刚体动力学方程可表示成如下形式:
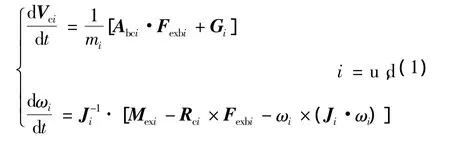
式中 Fexb为除重力外其他合力在弹体系中的投影,包括气动力、分离作用力、推力、结构约束力等;Gi为重力在分离惯性系中的投影;Abc为分离体弹体系到分离惯性系的转换矩阵;Rc为真实质心在其弹体系中的位置矢量。

下文分析相对运动特性时的理论质心运动状态可以通过与真实质心的相对关系得到,文中不再赘述。
3.2 级间分离运动特征值
为了预示分离运动状态,分别计算两级相对距离作为判断碰撞的依据;计算上面级攻角与侧滑角评估上面级姿态受到的扰动;计算两级轴线夹角预测分离过程两级气动干扰的程度。
3.2.1 相对距离
如图2所示,将分离面最小间隙ΔL定义为两级相对距离,即当ΔL<0时,认为两级发生碰撞。
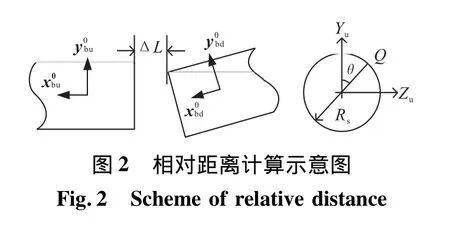
在上面级底面与下面级顶面边线上分别取n个点,记为 Qi,i=1,…,2n。i=1,…,n 为上面级底面边线上的点,根据式(4)、式(5)分别计算这些点与下面级顶面的距离,记为 ΔLi,i=1,…,n。i=n+1,…,2n为下面级顶面边线上的点,分别计算这些点与上面级底面的距离,记为 ΔLi,i=n+1,…,2n。两级分离面最小间隙可以表示为
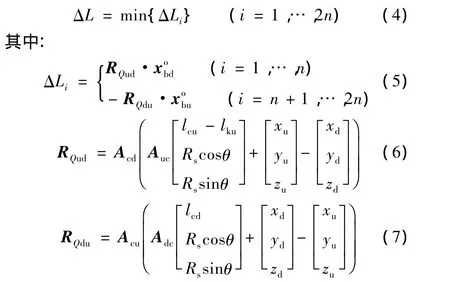
式中 lcu为上面级理论质心与其理论尖端的距离;lku为上面级长度;lcd为下面级理论质心到下面级理论头部的距离。
3.2.2 质心相对速度
质心相对速度Vr定义为两级理论质心在分离惯性系中的相对速度于上面级轴线上的投影:
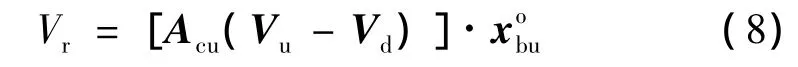
3.2.3 轴线夹角
轴线夹角δr定义为两级弹体系X轴方向单位矢量之间的空间夹角:
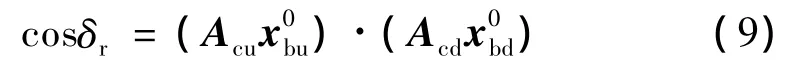
3.2.4 上面级攻角与侧滑角
上面级攻角αu与侧滑角βu:
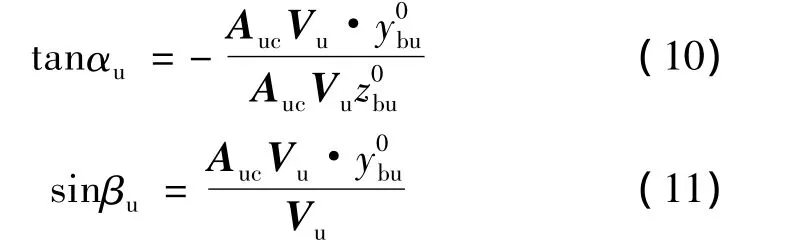
4 算例
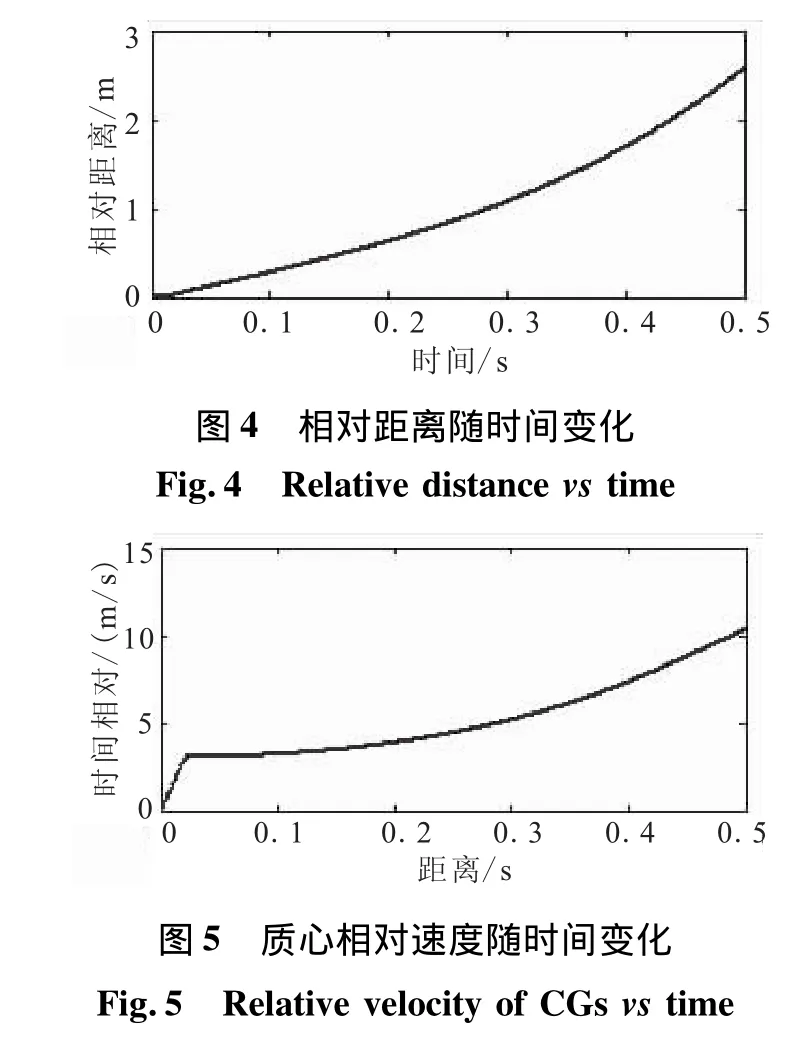
以某串联轴对称高超声速验证飞行器助推分离过程为例,分离方案如图3所示。试飞器质量约为500 kg,助推器在关机点质量约为1 000 kg。飞行器在助推发动机关机5 s后发出级间分离指令,飞行速度约为Ma=5,高度约20 km,分离装置在相对距离3 cm内为两级分别提供50 kN的轴向分离力。理想状态分离过程如图4、图5所示。

4.1 仿真输入条件
本算例在蒙特卡洛仿真中共考虑了53项输入偏差,分别是分离条件偏差10项、弹体质量特性偏差20项、弹体结构外形偏差4项、气动系数偏差12项、分离装置特性偏差7项,所有偏差均服从均匀分布,这样得到的结果更为保守。部分偏差输入值如表1所示。

表1 级间分离主要偏差Table 1 Parts of separation model uncertainties
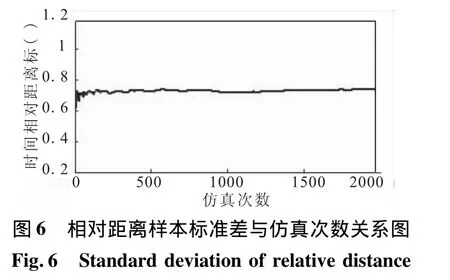
为了对分离系统进行充分评估,此次研究共执行了1 400次随机输入的分离过程仿真。蒙特卡洛仿真次数由分离过程关键量的统计特性来决定[5],图6为相对距离样本标准差与仿真次数的关系图,可以看到在大约1 400次仿真后,样本标准差已基本不再波动。
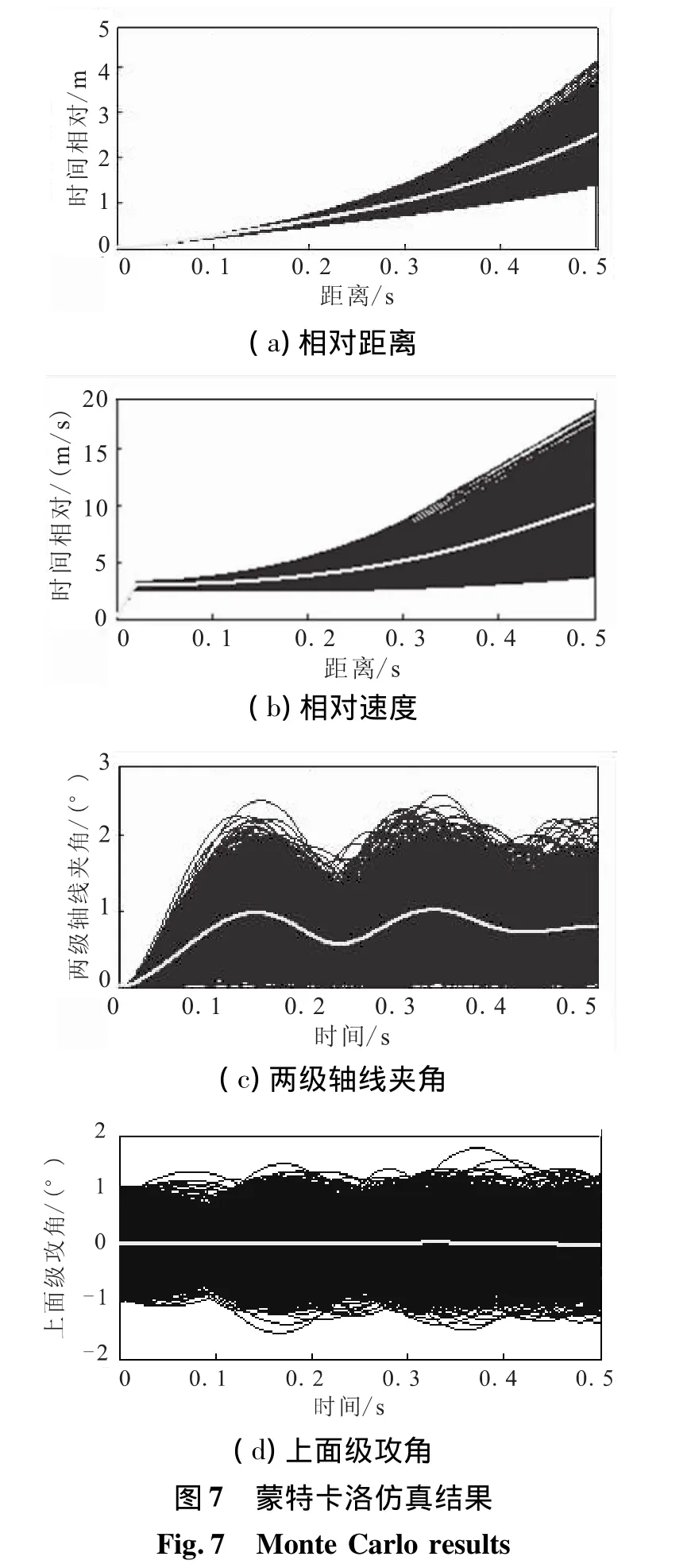
4.2 仿真结果分析
图7为1 400次蒙特卡洛仿真结果曲线,浅色粗线代表特征值的均值曲线。
取开始分离后0.5 s为仿真截止时间,可根据样本曲线统计得到的分离过程关键值变化范围与超出特定范围的概率,如表2、表3所示。表3中Ds为分离面直径,当相对距离小于4.2Ds时,下面级气动力仍受到上面级尾流的影响[7]。
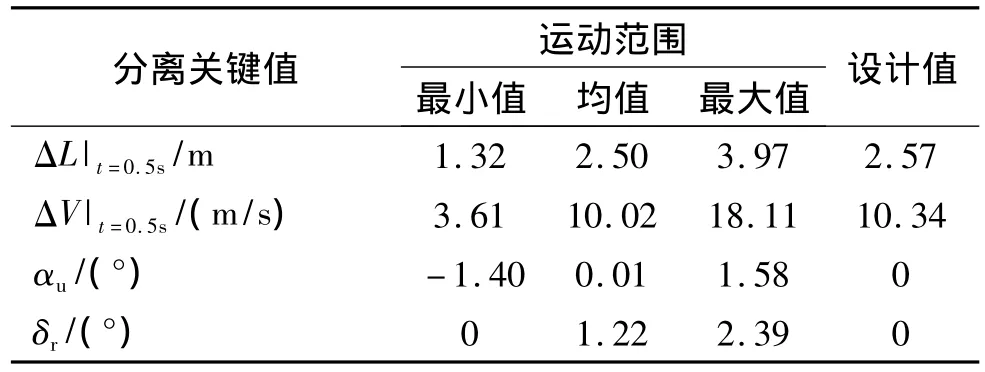
表2 分离过程运动范围Table 2 Movement range during separation process
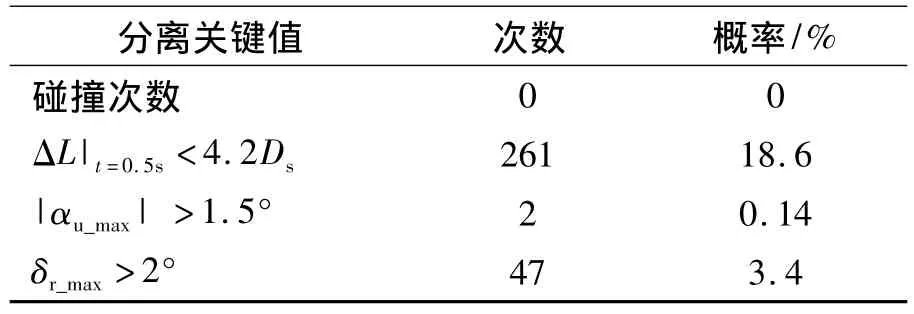
表3 分离过程特征概率Table 3 Character probability of separation process
针对算例所描述的分离问题,仿真结果显示:
(1)两级质心相对运动变化较平稳(图7(a)),0.5 s时相对距离最小为1.32 m(表2),两级没有碰撞发生(表3)。值得注意的是,通过 ΔL|t=0.5s<4.2Ds的概率可以看出,在0.5 s时下面级有18.6%的可能仍受到上面级尾流的影响。
(2)上面级姿态变化比较剧烈,攻角最大值达到了 1.58°(图7(d)、表2);轴线夹角在0.15 s以前上升到最大值 2.39°(图 7(c)、表2)。
5 结论
(1)在高动压条件下,随机偏差干扰主要影响分离过程的姿态运动,其攻角与轴线夹角变化剧烈,进而直接影响上面级起控过程,是分离系统设计必须关注的关键参数。
(2)根据蒙特卡洛仿真结果可得到在输入条件存在随机耦合偏差时分离过程关键参数(如相对距离、攻角、轴线夹角)的样本曲线,实现对近似真实条件下的分离运动范围、分离过程可能出现的极值大小与概率进行定量预测,从而达到检验分离系统性能、预示分离过程风险的目的。
[1]Reubush D E,Martin J G,Robinson J S,et al.Hyper-X stage separation-simulation development and results[R].AIAA 2001-1802.
[2]Tartabini P V,Bose D M,McMinn J D,et al.Hyper-X stage separation trajectory validation studies[R].AIAA 2003-5819.
[3]Lien J P,Bose D M,Martin J G.Automated sensitivity analysis of Hyper-X(X-43A)separation simulation[R].AIAA 2004-4930.
[4]Tartabini P V,Bose D M,Thornblom M N,et al.Mach 10 stage separation analysis for the X-43A[R].AIAA 2006-1038.
[5]Baumann E,Bahm C,Strivers B.The X-43A six degree of freedom Monte Carlo analysis[R].AIAA 2008-203.
[6]钱杏芳,林瑞雄,赵亚男.导弹飞行力学[M].北京:北京理工大学出版社,2008.
[7]周伟江,白鹏,马汉东.弹体级间分离流场特性的数值模拟研究[J].计算物理,2000,17(5).

