旋转固体火箭发动机燃烧室内流场分析解①

刘平安，王 革，郜 冶

(哈尔滨工程大学航天工程系，哈尔滨 150001)

0 引言

旋转过载引起固体火箭发动机性能的改变，一般有4种潜在的重要影响模式出现［1］:第1种模式是旋转加速过载引起壳体和药柱变形的力学模式(machanical mode);第2种为热力学模式(thermodynamic mode)，其导致燃烧性能的改变;第3种为应力模式(stress mode)，其导致推进剂燃速发生变化;第4种模态就是气动力模式(gas dynamic mode)，旋转过载将引起燃烧室和喷管的流动性能发生改变［2－8］。文献［9］研究了无限长圆柱形固体装药通道粘性不可压缩气体沿横截面气流切向速度分布的近似关系。对于有分布质量进入的旋转圆管内，切向速度分布类似Rankine涡。国内在旋转固体火箭发动机性能和流动特征方面也开展了广泛的研究［10－12］。文献［13－14］应用数值方法，研究了旋转固体火箭发动机的内流场，分析了旋转发动机内流场的分区特征和端面近轴区域的回流效应，研究了转数对涡核结构及端面流场细微结构的影响。

本文旨在应用解析分析法求解旋转情况下的发动机内部流场，分析旋转和壁面质量注入对涡核结构的影响。

1 数学物理模型

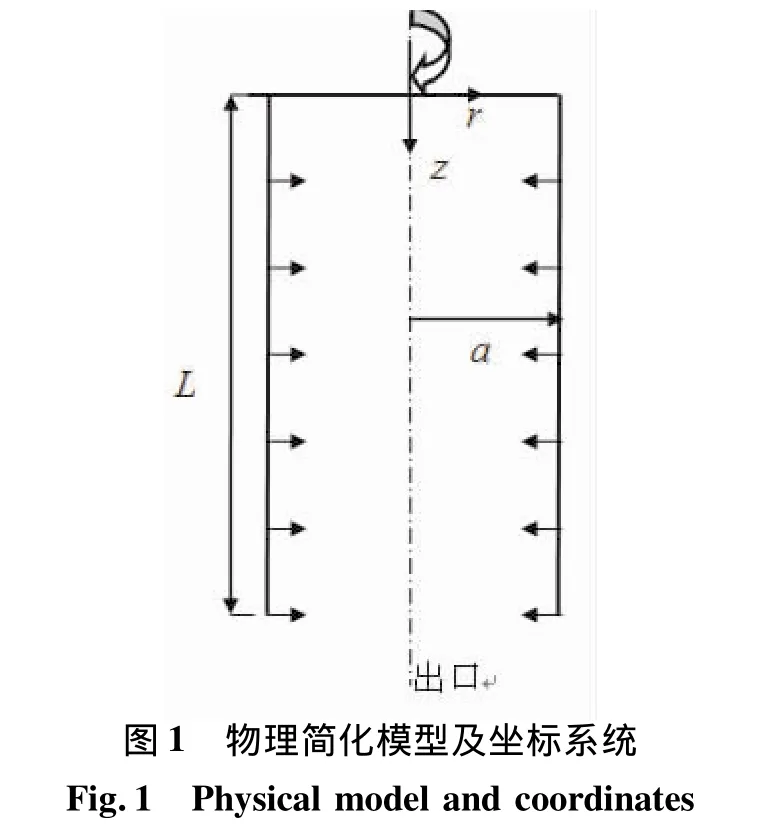
1.1 物理模型

轴对称管型装药内孔燃烧固体火箭发动机燃烧室通道空间的简化模型如图1所示，长为L，半径为a，头部封堵。燃烧室侧壁面有流体均匀注入，注入速度为Vb，发动机转速为ω，则侧面切向速度U=ωa。

1.2 基本假设

由于发动机旋转时，内流场变化较复杂，引入以下假设条件:

(1)流动处于稳定状态;

(2)流体等温不可压;

(3)忽略体积力;

(4)粘性系数ν为常数;

(5)忽略头部壁面摩擦影响。

1.3 控制方程

通用控制方程:

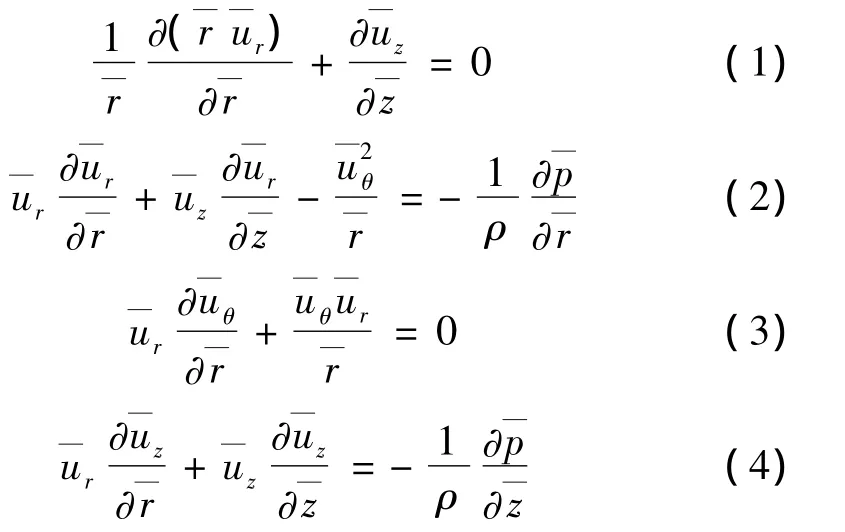
1.4 边界条件

1.5 参数无量纲化

为了更简洁地描述物理问题，下面将各参数无量纲化:

2 方程的解析求解

2.1 简化方程

将式(3)无量纲化，有

2.2 求解方程

2.2.1 方程的通解

运用分离变量法，认为:

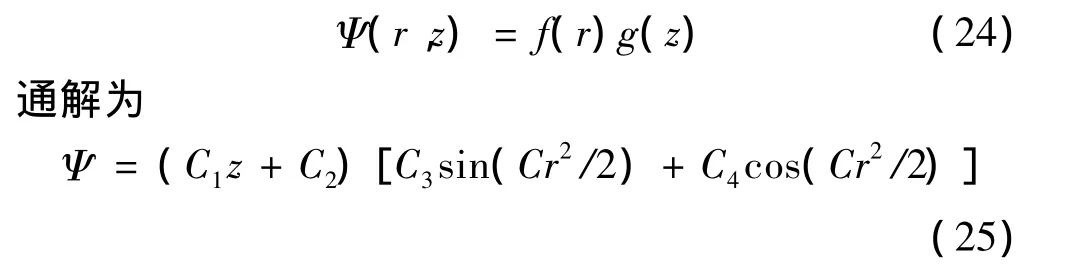
2.2.2 方程的特解

应用式(23)的边界条件确定常数:

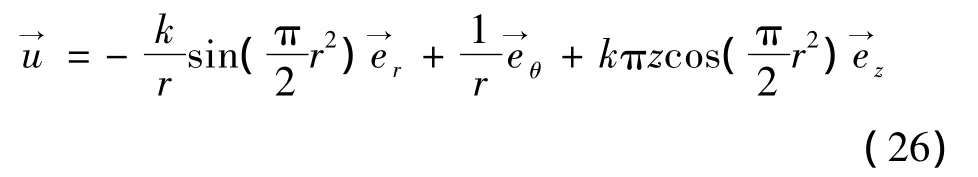
式(26)是满足全部边界条件的速度解。

2.3 修正切向动量方程

假设整个流场只存在自由涡，该假设虽然对径向与轴向速度的分布影响很小，但明显存在缺陷。完整的假设应包括外部自由涡与核心强制涡，核心强制涡的运动类似于刚体旋转，由于轴附近粘性力的作用而产生。为了得到准确的切向速度分布，需修正切向动量方程，在式(3)中引入粘性项。修正后的切向动量方程无量纲形式为

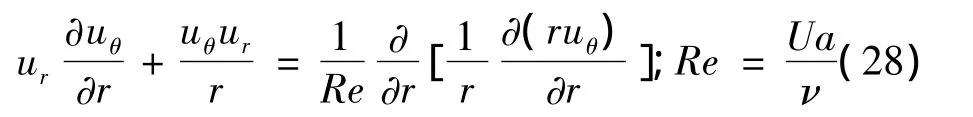
式中 Re为平均流动雷诺数。

令 uθ=uθ(r)，式(28)化为常微分方程:

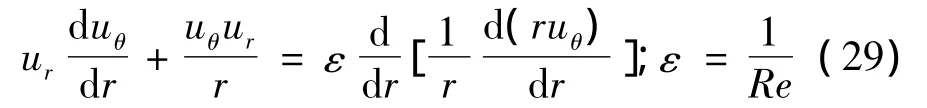
引入2个边界条件:

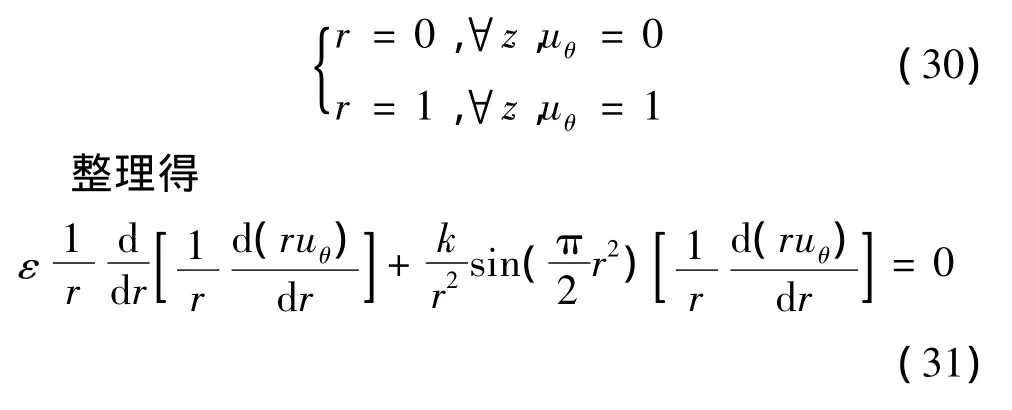
为了简化方程，令:

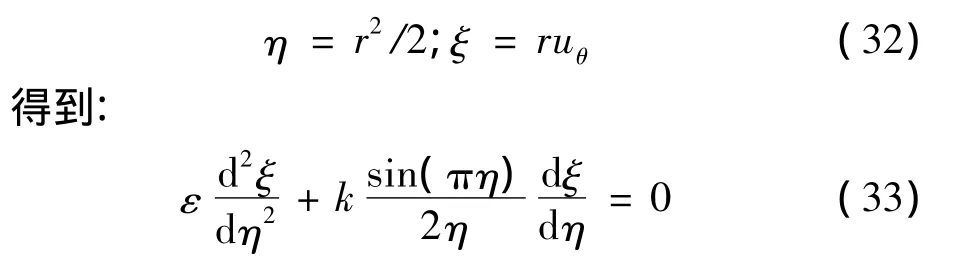
2.4 重新求解切向速度

实际情况中Re＞1 000，因此ε非常小，可作为摄动量，运用摄动法中的渐进展开匹配法求解切向速度:

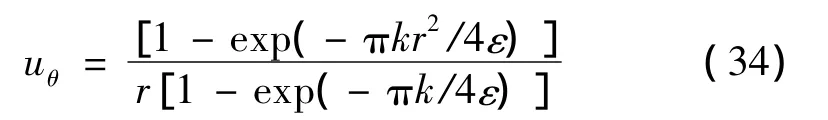
式(34)为切向速度的最终表达式。当ε→0时，切向速度与全场自由涡假设条件下得到的结果一致，即uθ=1/r。对于固定的 ε，当 r→0时，可将式(34)展开为

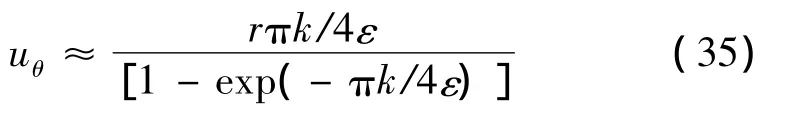
显然，uθ与r成正比，说明核心区流体类似于刚体做绕轴转动，这是由于集中的粘性力作用。应注意到，前面得到的解明显受参数ε与k的影响，因此定义有效雷诺数ReV(注入雷诺数):

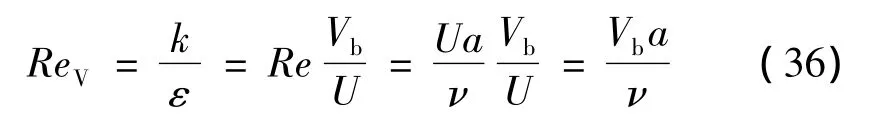
式(34)切向速度的表达式可写成ReV的表达形式:

2.5 粘性涡核厚度

为了确定强制涡的影响区域，首先要确定涡核半径r*。对式(34)求导可得，并令其等于0。

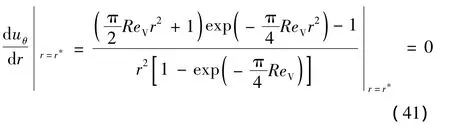
由此可得

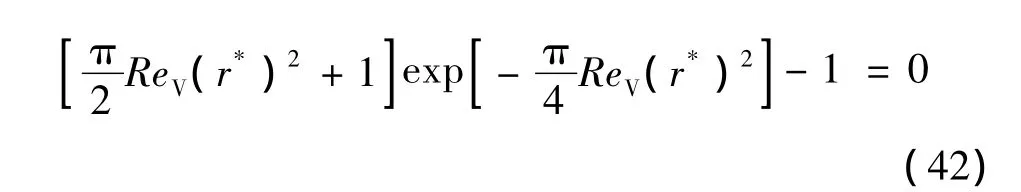
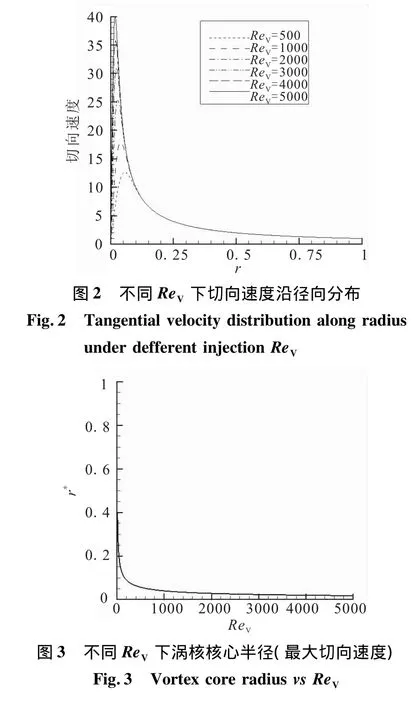
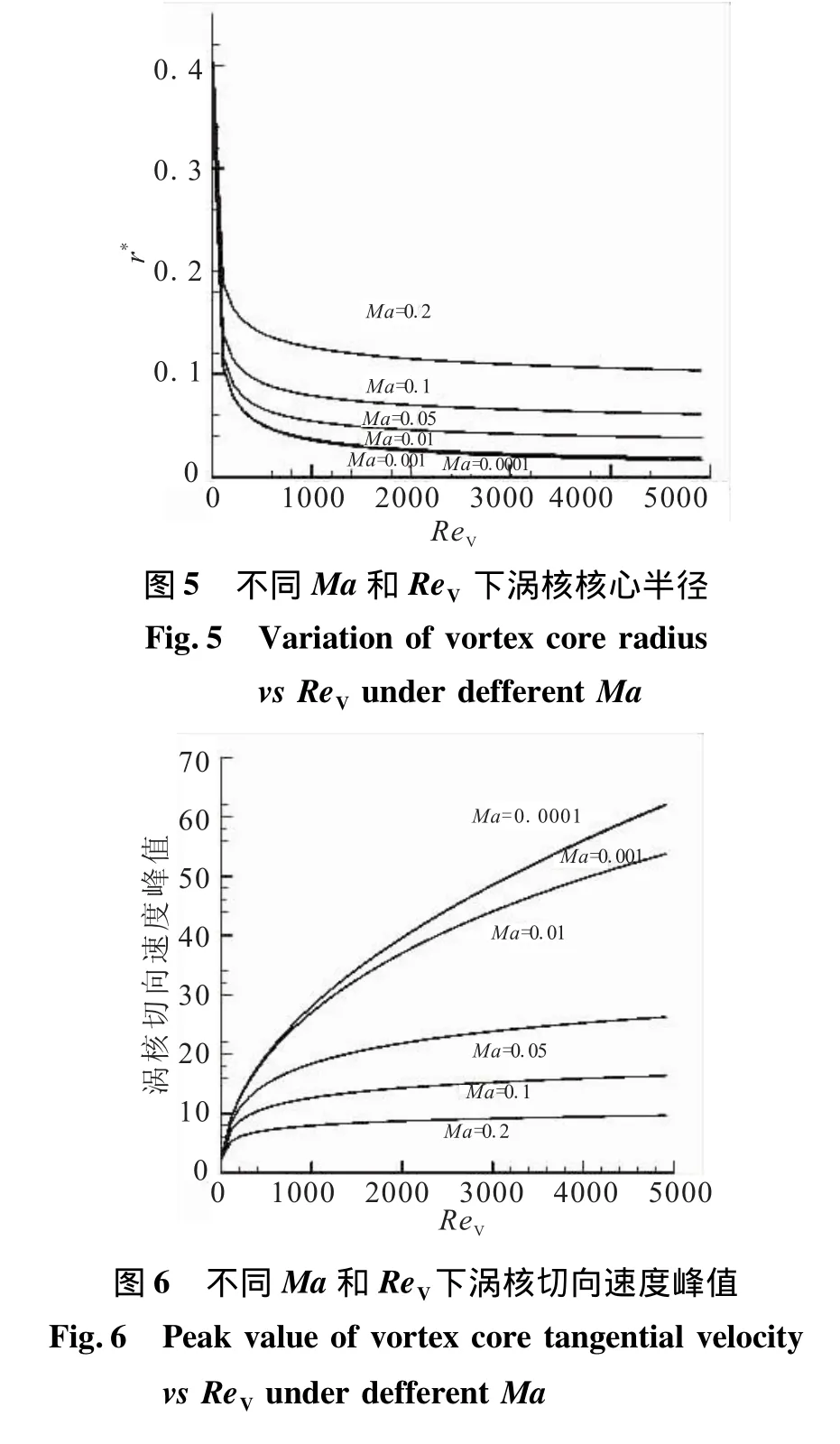
不同ReV下切向速度沿径向分布见图2;最大切向速度的位置，即涡核核心半径r*随ReV的变化见图3。当ReV超过500时，其涡核半径减小程度趋于平缓。小于500时，涡核半径变化加大。当注入速度一定的情况下，湍流比层流的粘性系数大得多，对应的ReV相应减小。因此，湍流的涡核半径比层流情况下大很多，湍流强度越大，对应的涡核区也就较大。

2.6 切向速度的近似关系

式(34)可写成如下近似关系:

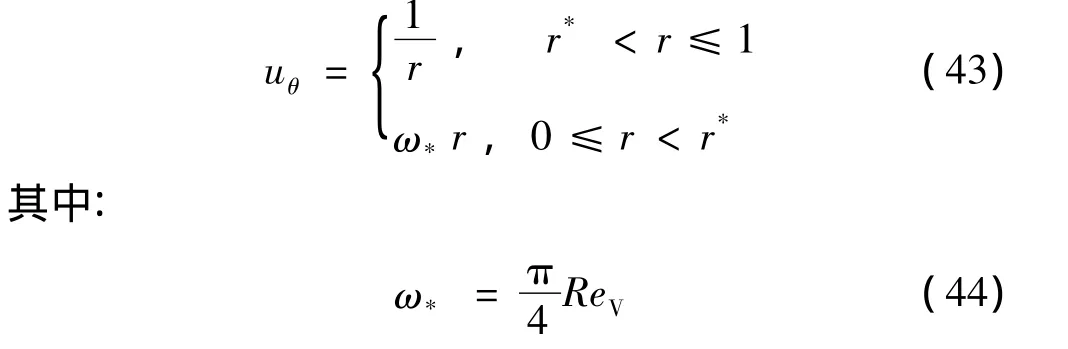
由r*处的连续条件ω*(r*2)=1可得

相应于式(43)，一般在ReV＞103的情况下，通道内不可压缩燃气的切向流动速度在2个区域内具有不同的特点，在小于r*的圆柱气流核心区，切向速度呈“准固体”特征，其旋转角速度ω*明显超过通道旋转角速度ω。而大于r*的区域切向流动为自由旋流。由于在旋转角速度很高的情况下，不可压缩的假设会带来较大的误差，因此对高速旋转的通道，应考虑可压缩性的修正。

2.7 切向速度的可压缩性修正

文献［9］分析了可压缩气体在旋转通道内的切向速度横截面压力分布，首先定义核心旋转角速度:

即当音速c→∞，ω*等于不可压缩流体的结果。r*的确定同式(45)。不同马赫数下涡核转速ω*随ReV的变化见图4。

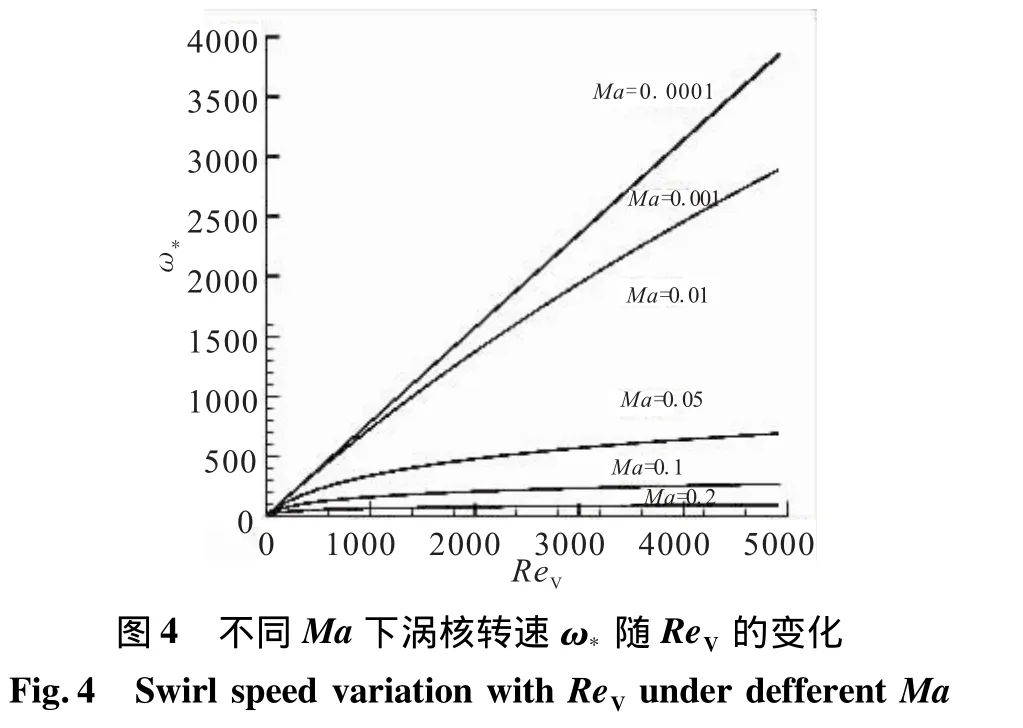
由图4可看出，可压缩性对涡核结构的影响较大，随旋转速度增大，可压缩的影响加剧，涡核转速对ReV的依赖程度急剧减小，并趋于平缓。而涡核半径随转速的增加而增加，尤其对于较大的ReV，当ReV＜200时，涡核半径随ReV的增大急剧减小，见图5。图6为涡核切向速度峰值与ReV和旋转马赫数(与转数相对应)的关系。

2.8 求解压力和涡量

根据式(2)与式(4)，压力梯度可表示为

积分式(51)与式(52)，且合并:

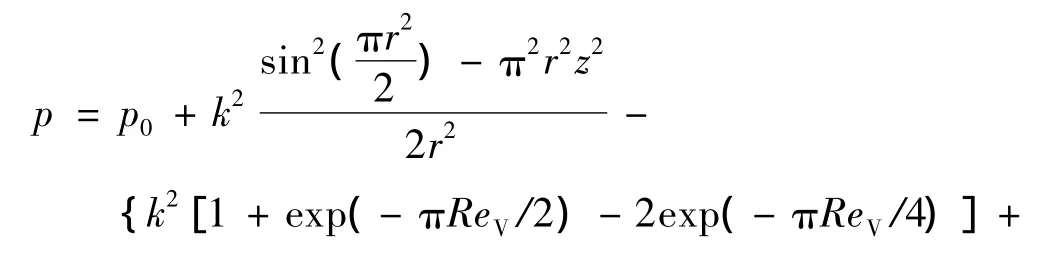
由于重新求解了切向速度，因此涡量表达式(13)也要相应地发生变化，根据式(39)与式(9)，可得到修正后的涡量表达式为

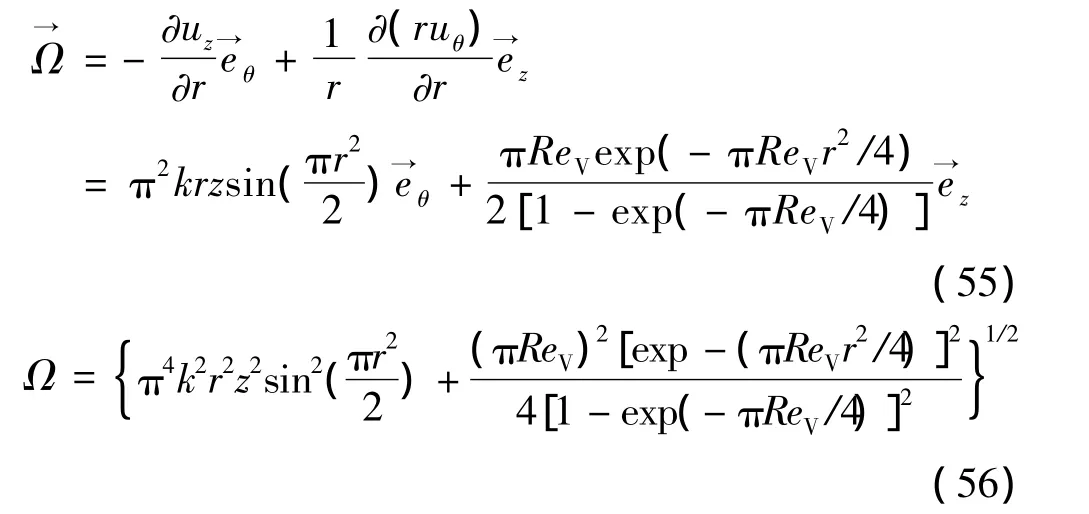
3 结论

(1)通道内不可压缩燃气的切向流动速度在2个区域内具有不同的特点，在小于r*的圆柱气流核心区，切向速度呈“准固体”特征，其旋转角速度ω*明显超过通道旋转角速度ω;而大于r*的区域切向流动为自由旋流。

(2)由于在旋转角速度很高的情况下，不可压缩的假设会带来较大误差，因此对高速旋转的通道，应考虑可压缩性的修正。可压缩性对涡核结构的影响较大，随着旋转速度的增大，可压缩的影响加剧，涡核转速对注入雷诺数的依赖程度急剧减小，并趋于平缓。而涡核半径随转速的增加而增加，尤其对于较大的ReV。

［1］Langhenry M T.Acceleration effects in solid propellant rocket motors［J］.AIAA Journal，1986，15:77-90.

［2］Mager A.Approximate solution of isentropic swirling flow through a nozzle［J］.ARS Journal，1961(8):1140-1148.

［3］Bastress E K.Interior ballistics of spinning solid propellant rockets［J］.J.Spacecraft Rockets，1965(3):12-25.

［4］Manda L J.Spin effects on rocket nozzle performance［J］.Spacecraft Rockets，1965(3):36-45.

［5］Nontan D J.An analytical and experimental investigation of swirling flow in nozzle［J］.AIAA Journal，1968(10):102-110.

［6］Dunlap R.An investigation of the swirling flow in a spinning end-burning rocket［J］.AIAA Journal，1969，7(12):2293-2299.

［7］Fuchs M D.A parametric study of the effects of acceleration on the burning rate of metalized solid propellants［J］.Journal of Spacecraft and Rockets，1982，19(6):539-544.

［8］Boraas S.Modeling slag deposition in the space shuttle solid rocket Motor［J］.Journal of Spacecraft and Rocket，1984，21(11):36-47.

［9］莱兹别格B A，叶罗欣B T，沙母索诺夫K п.固体火箭发动机系统工作过程的理论基础［M］.刘光宇，梅其志，译.北京:国防工业出版社，1984:369-392.

［10］邵爱民.大型固体发动机旋转试车头部热防护工程分析［J］.固体火箭技术，1998，21(3):7-12.

［11］蔡国飙，田辉.旋转对固体火箭发动机的影响［J］.推进技术，1999，20(1):11-15.

［12］高波，叶定友，侯晓.旋转固体发动机燃烧室燃气湍流流动数值模拟［J］.推进技术，1999，20(6):23-27.

［13］王革，陈亮，郜冶，等.旋转对固体火箭发动机燃烧室燃气流动的影响［J］.空气动力学学报，2008，26(2):208-211.

［14］王革，陈亮，郜冶.旋转管状装药固体火箭发动机燃烧室流动特征［J］.弹道学报，2008，20(3):5-8.