高超声速飞行器的自适应容错控制①

宋 超，赵国荣，刘 旭

(1.海军航空工程学院控制工程系，烟台 264001;2.海军航空工程学院 青岛分院，青岛 266041)

0 引言

近几年来，高超声速飞行器作为突破导弹防御系统并实现远程精确打击的新途径受到了广泛的关注［1］。飞行器的执行部件由于频繁执行工作任务且工作环境恶劣，很容易发生故障，会严重影响系统性能，甚至造成整个控制系统的不稳定。因此，对执行器故障进行容错控制研究具有重大的现实意义，且是近年研究的热点。

容错控制一般分为主动容错控制和被动容错控制［2］。目前文献中，自适应滑模控制、鲁棒控制及反演控制等多种先进控制策略应用到非线性系统容错控制中，且在航天器姿态控制方面取得一定的成果［3－5］。文献［6］采用滑模观测器估计系统的状态，并根据估计值在线调整切换增益，避免了高频抖振，但文中只是将故障看做是未知动态进行控制器的设计。文献［7］针对一类多输入多输出系统存在不确定故障问题提出了一种自适应容错控制方法，但未考虑系统存在不确定项及外界干扰的情况。文献［8］提出一种鲁棒自适应容错控制，使得带有界干扰的系统在存在故障时渐进稳定，但该方法参数设置依赖于执行器故障信息，且需要求解包含不确定变量的Lyapunov方程。文献［9］提出一种新的容错控制算法，该方法解决了系统存在未知外界干扰的问题，且不需求解带有时变、不确定变量的Lyapunov方程，但是该方法仅用于线性系统。

本文提出了一种新的自适应容错控制方法，该方法不需要知道系统非线性函数及未知干扰的上界，且能保证执行器发生故障时，系统渐进稳定，并将该控制方法应用于一类具有外界扰动的飞行器的执行器存在卡死或部分失效故障的问题研究中。

1 飞行器及故障模型描述

1.1 飞行器数学模型的建立

为了使描述飞行器在空间的六自由度运动方程不过于复杂，作如下假设:

假设1 不考虑飞行器的挠性，即视为刚体。

式中 α、β、γv为飞行器的攻角、侧滑角和速度滚转角;ωx、ωy、ωz为飞行器绕弹体坐标系转动角速度;δx、δy、δz为等效舵偏角。

建立飞行器运动学和动力学方程如下:

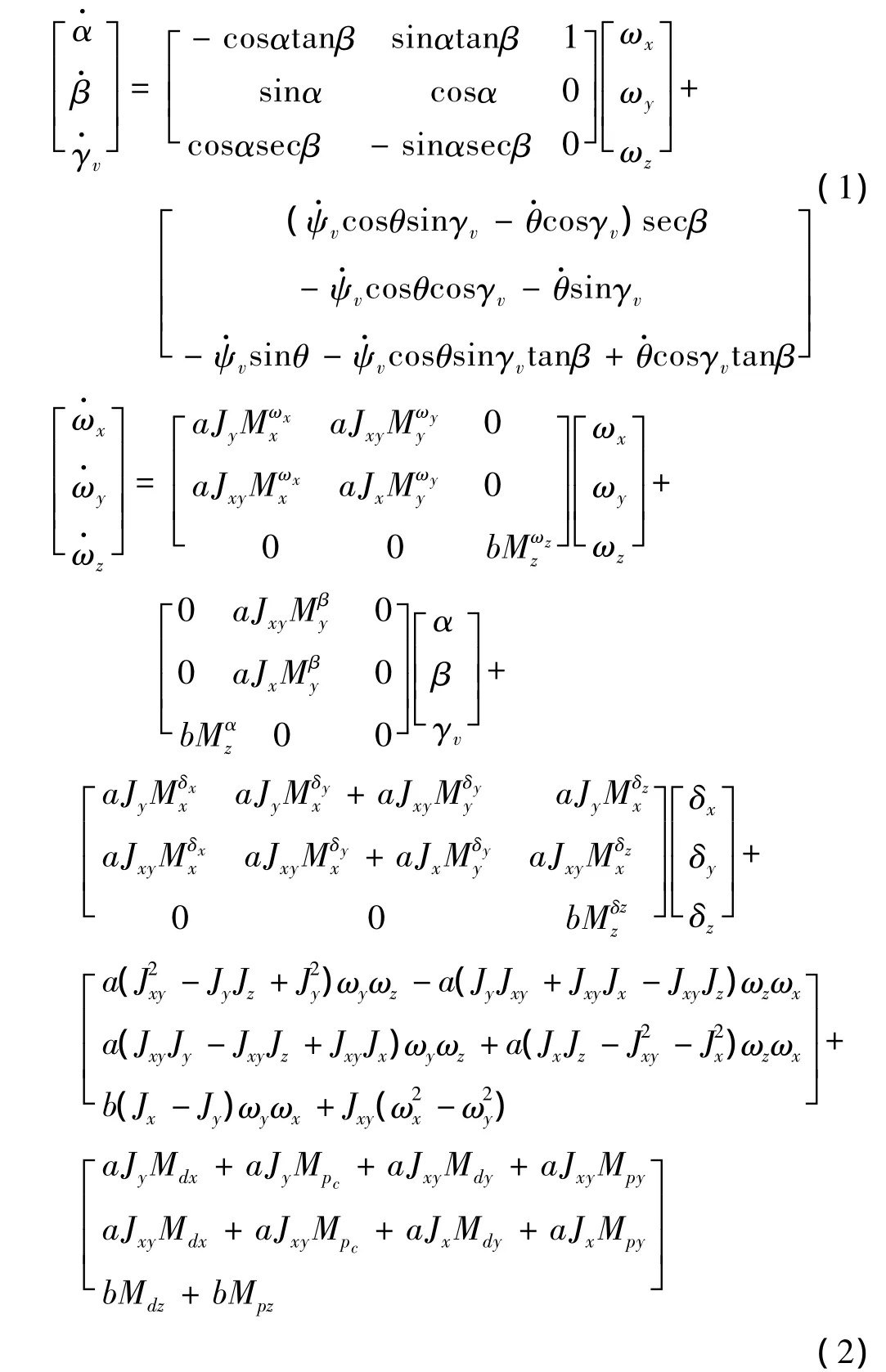
简记式(1)和式(2)，并考虑气动参数的不确定性，则系统模型可写成:

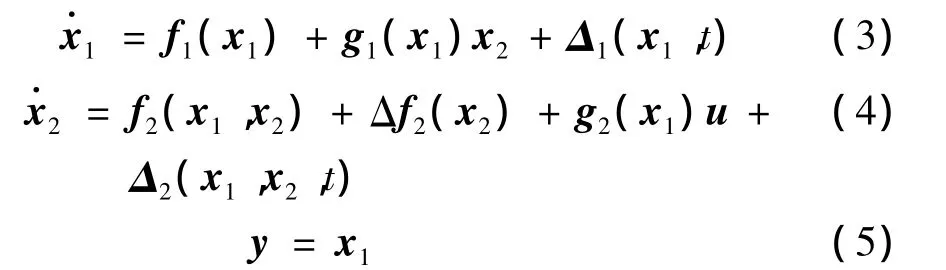
式中 f1(x1)、f2(x1，x2)、Δf2(x2)、g1(x1)、g2(x1)为对应的矩阵;Δ1(x1，t)、Δ2(x1，x2，t)为非匹配不确定项。

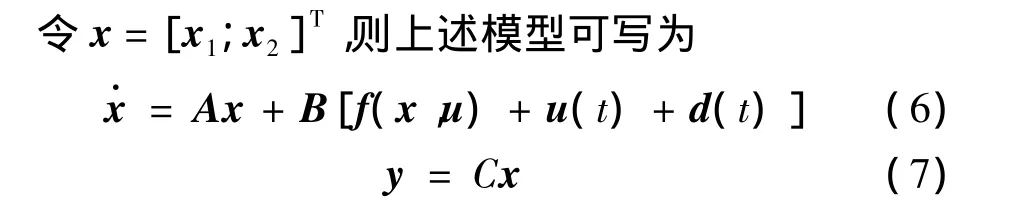
式中 A、B、C定义为系统的状态矩阵、输入矩阵和输出矩阵;f(x，u)为光滑非线性函数;d(t)为建模不确定性和未知外界干扰。

1.2 故障描述

系统执行器故障表示如下形式［12］:

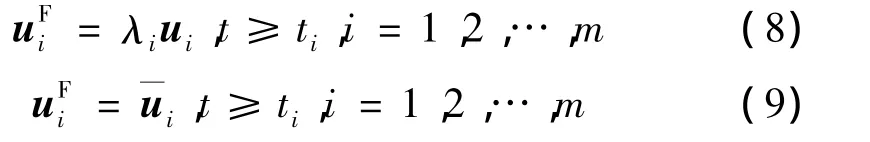
式(8)表示系统执行器部分失效，0＜λi≤1为执行器有效部分的比例;式(9)表示系统执行器卡死失效，此时为某一常数。执行器存在故障(8)和故障(9)时，系统的控制输入u可表示为

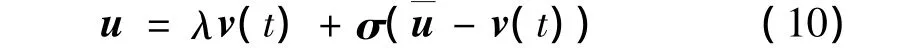
式中 v(t)=［v1(t)，…vm(t)］T为待设计控制输入;λ=diag［λ1，…，λm］;σ =diag［σ1，…，σm］，当第 i个执行器发生卡死故障时，σi=1，否则 σi=0，i=1，…，m=［，…］T。

定义 ρ =diag［ρ1，…，ρm］，其中 ρi= λi－ σi，i=1，…，m，则有ρ=λ－σ。定义 Δ=σ，由定义可知，Δ为范数有界，设‖Δ‖≤δΔ，δΔ为未知正常数。则式(10)改写成

飞行器控制系统的任务是在不超过控制执行机构所能提供的控制量的限制的前提下，实现对制导系统给出的气流角指令yd的跟踪［13］。

2 容错控制律设计

假设2 存在常矩阵K0，使得A－BK0为Hurwitz矩阵。

假设3 存在对称正定矩阵P和Q，满足:

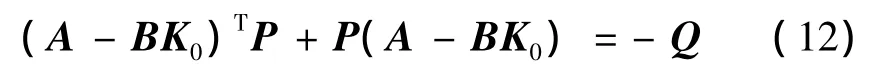
假设4 非线性函数f(x，u)及外界干扰满足范数有界:

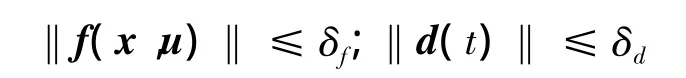
式中 δf、δd为未知正常数。

定义容错控制律［14］:

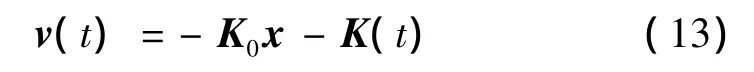
其中:

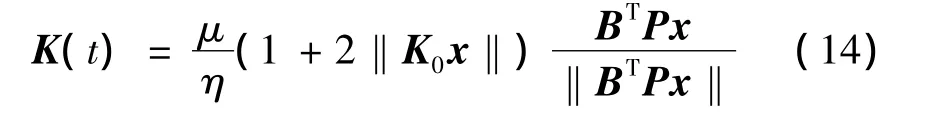
式中 η≤min{ρ1，…，ρm};μ =max{1，δΔ+δf+ δd}。

则当系统存在如式(8)和式(9)的执行器故障时，则可表示如下:

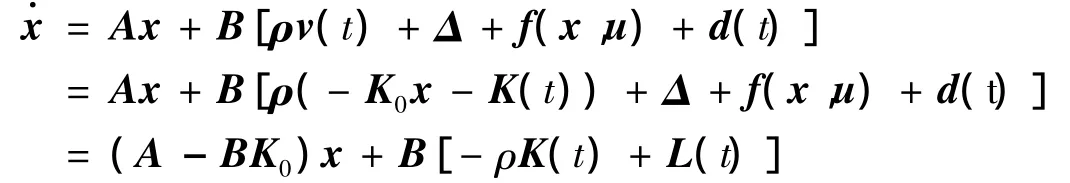
其中，L(t)=(I－ρ)K0x+f(x，u)+d(t)+Δ。

由假设4可得

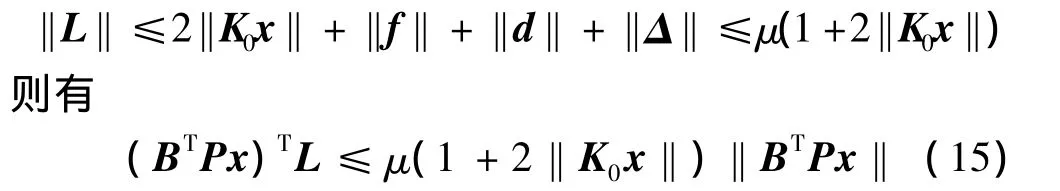
考虑如下形式的Lyapunov函数:

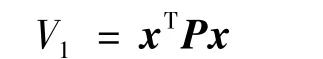
对V1求导并应用假设3和式(14)得

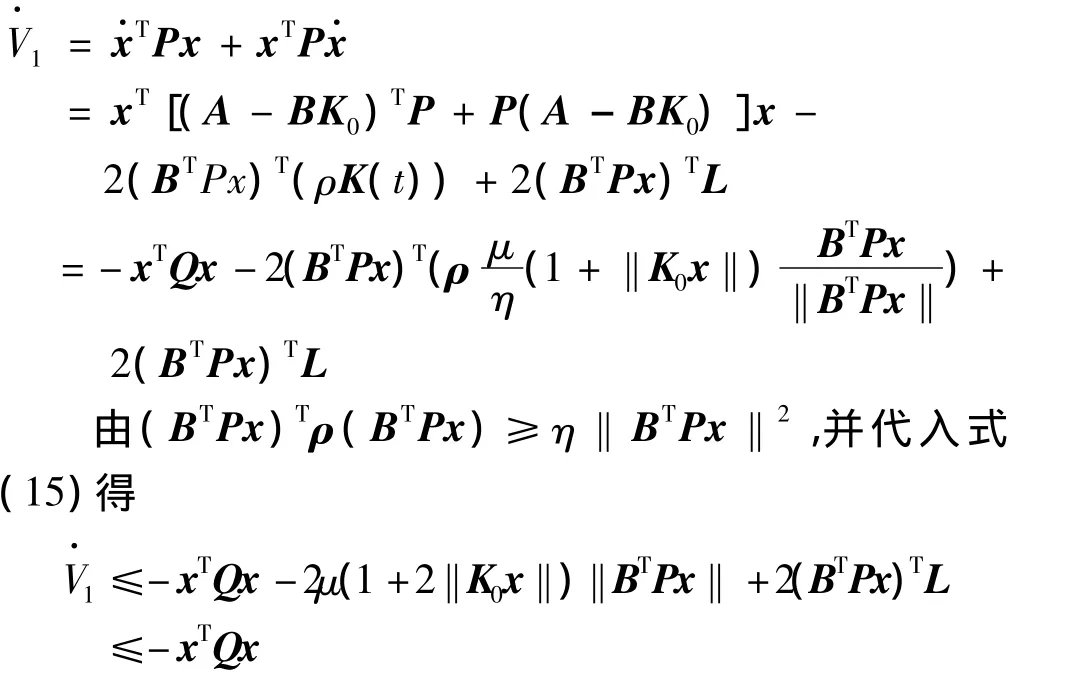
由Lyapunov稳定理论容易得出，该容错控制律可使系统全局渐进稳定。

以上控制器设计过程中，需要已知干扰项及故障输入的上界，即要求μ已知，而实际情况下，该上界往往难以已知。因此，设计过程中一般考虑最坏的情况，这必然带来一定的保守性。针对该问题，研究以下自适应容错控制方法。

3 自适应容错控制器设计

定义鲁棒自适应容错控制律为如下形式:

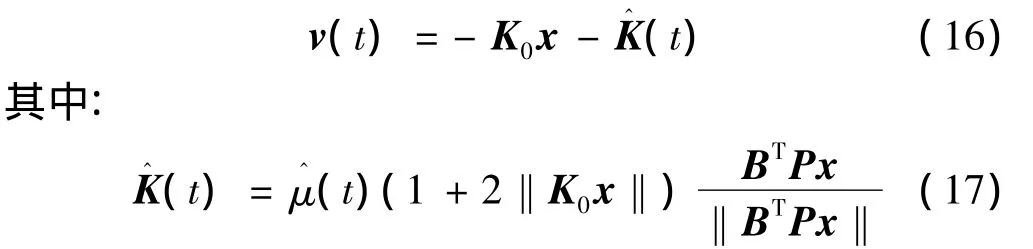
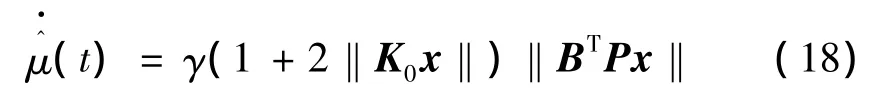
式中 γ为待设计正常数。

考虑如下形式的Lyapunov函数:

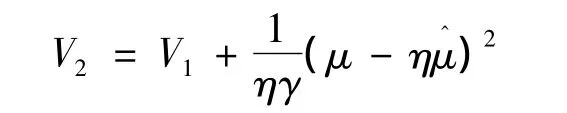
对V2求导并应用假设3和式(17)得

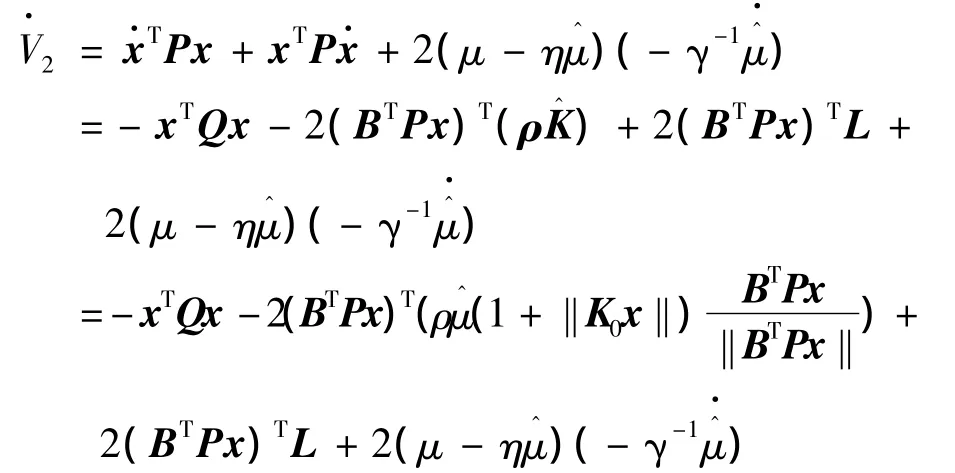
由(BTPx)Tρ(BTPx)≥η‖BTPx‖2，并代入式(18)，则上式得

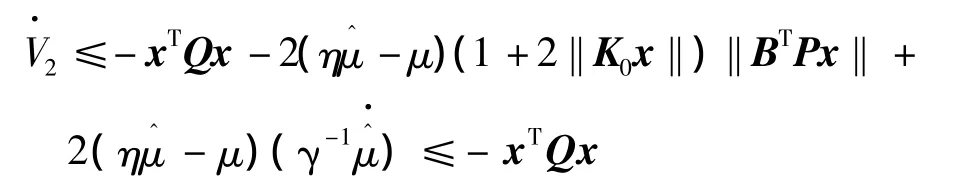
由Lyapunov稳定理论容易得出，自适应容错控制律(16)可使系统渐进稳定。

采用以上参数自适应律避免了干扰项及故障输入的上界精确已知的局限性。

4 仿真验证

飞行器模型和气动参数来自NASA报告［15］。为使飞行器模型不过于复杂，仿真时将高超声速飞行器模型基于小扰动原理进行近似线性化处理。为了简化控制器设计，忽略惯性积项。取主惯量Jx=1 000，Jy=7 600，Jz=7 700;取 γ =10(0)=0.5。初始条件x1(0)=［0.2° 0.2° 0.2°］T，x2(0)=［0 0 0］T;期望跟踪信号 yd=［2.3° 0 0］。

考虑下列3种模式:

模式一:所有执行器正常，此时λ=I;σ=0;ρ=I。

模式二:t＜5 s时，执行器正常运行;t＞5 s时，两执行器部分失效，并设有效部分比例分别为λ1=0.3，λ2=0.5。

模式三:t＜5 s时，执行器运行正常，t＞5 s时，执行器一发生卡死故障，执行器二正常运行。

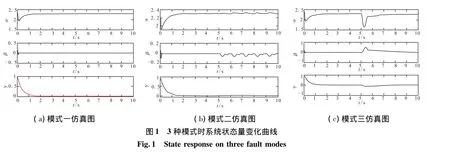
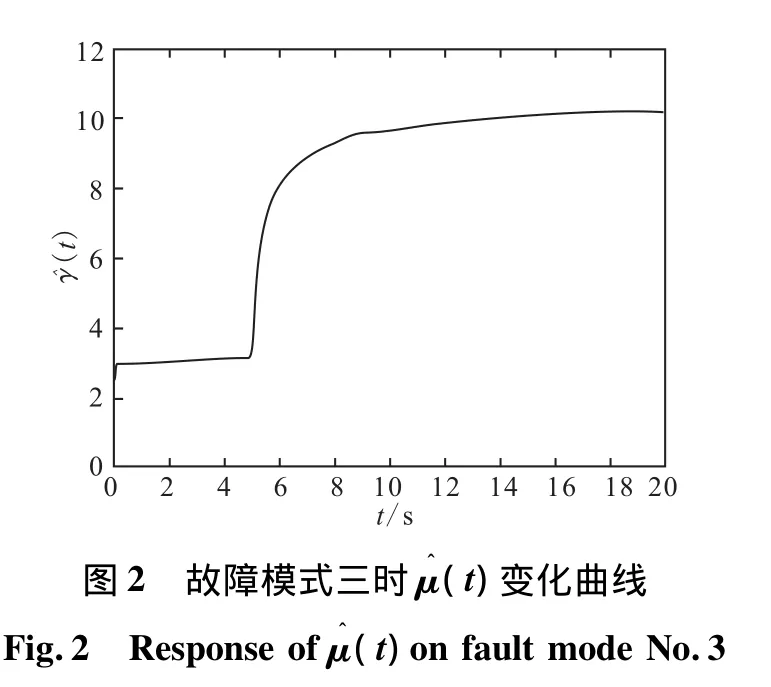
仿真结果如图1和图2所示。

从图1可看出，无论执行器存在部分失效还是卡死故障时，本文设计的自适应容错控制律可使飞行器渐进稳定于期望的姿态角，即实现对期望制导指令的鲁棒输出跟踪。仿真图2表明，未知参数μ^(t)通过在线估计，能随着故障信息自适应的变化。

5 结论

(1)设计了一种自适应容错控制方法，该方法不需要已知非线性函数及未知干扰的上界，而是采用自适应法对其估计;并通过Lyapunov方法证明了该控制器在存在执行器失效或卡死故障时，系统仍渐进稳定。

(2)分析了飞行器再入过程中可能出现的执行器故障问题，应用本文所述自适应容错控制方法，实现制导指令的鲁棒输出跟踪，并通过仿真验证了该控制器对飞行器执行器部分失效或卡死故障都具有良好的容错能力。

［1］Jorris T R.Common aero vehicle autonomous reentry trajectory optimization satisfying waypoint and no-fly zone constraints［D］.Alabama:Air University，2007.

［2］周东华，Ding X.容错控制理论及其应用［J］.自动化学报，2000，26(6):788-797.

［3］Hu Q L，Zhang Y M，Huo X，et al.Adaptive integral-type sliding mode control for spacecraft attitude maneuvering under actuator stuck failures［J］.Chinese Journal of Aeronautics，2011，24:32-45.

［4］Jiang Y，Hu Q L，Ma G F.Adaptive backstepping fault-tolerant control for flexible spacecraft with unknown bounded disturbances and actuator failures［J］.ISA Transactions，2010，49:57-69.

［5］Godard，Krishna D K.Robust attitude stabilization of spacecraft subject to actuator failures［J］.Acta Astronautica，2011，68:1242-1259.

［6］程月华，姜斌，孙俊，等.基于滑模观测器的卫星姿态控制系统滑模容错控制［J］.上海交通大学学报，2011，45(2):190-194.

［7］Tang Xi-dong，Tao Gang，Suresh M Joshi.Adaptive actuator failure compensation for parametric strict feedback systems and aircraft application［J］.Automatica，2003，39:1975-1982.

［8］Jin X Z，Yang G H.Robust adaptive fault-tolerant compensation control with actuator failures and bounded disturbances［J］.Acta Automatica Sinica，2009，35(3):305-309.

［9］Fan L L，Song Y D.On fault-tolerant control of dynamic systems with actuator failures and external disturbances［J］.Acta Automatica Sinica，2010，36(11):1620-1625.

［10］钱杏芳，林瑞雄，赵亚男.导弹飞行力学［M］.北京:北京理工大学出版社，2008:28-48.

［11］赵汉元.飞行器再入动力学和制导［M］.长沙:国防科技大学出版社，1997:23-86.

［12］Tang Xi-dong ，Tao Gang ，Suresh M Joshi.Adaptive actuator failure compensation for nonlinear MIMO systems with an aircraft control application［J］.Automatica，2007，43:1869-1883

［13］陈洁，周绍磊，宋召青.基于不确定性的高超声速飞行器动态面自适应反演控制系统设计［J］.宇航学报，2010，31(11):2550-2556.

［14］Fan L L，Song Y D.Fault-tolerant control and disturbance attenuation of a class of nonlinear system with actuator and component failures［J］.Acta Automatica Sinica，2011，37(5):623-628.

［15］Shaughnessy J D，Pinckney S Z，McMinn J D，et al.Hypersonic vehicle simulation model:winged-cone configuarion［R］.NASA TM-102610，1990.