满足置换恒等式的强wrpp半群的结构

任 秀，金天坤，夏 晶

(大庆师范学院 数学科学学院，黑龙江 大庆 163712)

0 引言

很多学者对于满足置换恒等式的半群已经进行了深入的研究。Yamada给出了满足置换恒等式的半群的定义，并证明了满足置换恒等式的带是正规带，给出了满足置换恒等式的正则半群的结构，即满足置换恒等式的正则半群是交换正则半群与正规带的织积[1]；郭小江给出了满足置换恒等式的富足半群的结构——满足置换恒等式的富足半群是正规带与C-半群的织积，其中C-半群是交换半群并且是可消半群的强半格[2]，并且将可置换性与rpp半群二者联系起来，引入了PI-强rpp半群(满足置换恒等式的强rpp半群)，同时证明了PI-强rpp半群是正规带与交换可消幺半群的织积[3]；唐向东引入了广义格林关系——A**-关系[4]，利用这一新格林关系给出了一类更广义的C-rpp半群的刻划，即C-wrpp半群类，并给出了C-wrpp半群的结构定理，即S是C-wrpp半群当且仅当S是一族P-左可消幺半群的强半格。C-wrpp半群是对Clifford半群和C-rpp半群的更深入的推广；任秀等将可置换性与wrpp半群二者联系起来，引入了满足置换恒等式的强wrpp半群，得到了满足置换恒等式的强wrpp半群的一些重要性质和特征，满足置换恒等式的强wrpp半群的子半群仍满足置换恒等式，以及其幂等元是正规带[5]，并且通过引入正规带上的最小半格同余ε，证明了当E(S)是矩形带时，满足置换恒等式的强wrpp半群是交换P-左可消幺半群与矩形带的直积[6]。本文通过建立满足置换恒等式的强wrpp半群S上的一个半格同余ρ，证明了满足置换恒等式的强wrpp半群是交换P-左可消幺半群与矩形带的直积的强半格。

1 基础准备

1.1 基本定义

定义 1[4]：设S是一个半群，S上的广义格林关系A**可以等价地定义如下：

A**={(a，b)∈S×S| (∀x，y∈S1) (ax，ay)∈P⟺(bx，by)∈P}，这里P表示通常的格林关系。

定义2[7]：半群S称为wrpp半群，如果半群满足下列条件：

1)半群S的每个A**类至少含有S一个幂等元；

2)对于所有的e∈Ma，有a=ae，其中Ma=E(S)∩Aa**，E(S)是S的幂等元集。

我们注意到有A⊆A**，A*⊆A**成立，这里A是普通的格林关系，A*是格林*-关系。特别地，当S是wrpp半群时，有eA**f当且仅当eAf，e，f∈E(S).

定义3[5]：强wrpp半群，如果对于任意的a∈S存在唯一与a有A**关系的幂等元e，使得ea=a。

如果S是强wrpp半群,Ma总是含有唯一的幂等元e，使得a=ea，我们标记包含在Ma中的这个唯一的幂等元e为a+。因此，有a=a+a=aa+。

定义4[2]：设S是一个半群，A是S一个子集，令

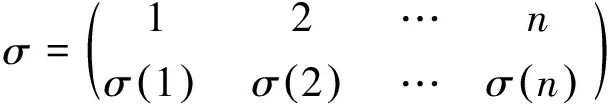
是一个n元非恒等置换。称A为满足由σ决定的置换恒等式(简称A满足置换恒等式) 。如果关于任意x1，x2，…，xn∈A，都有

x1·x2·…·xn=xσ(1)·xσ(2)·…·xσ(n)

其中x1，x2，…xn∈S，如果A=S，称S是满足置换恒等式的半群。

本文主要研究满足置换恒等式的强wrpp半群的结构，如无特别声明，S总表示一个满足置换恒等式的强wrpp半群。令

则σ(k)=m，m>k。关于e∈E(S)，记

Se={a∈S|a+=e}

定义5[4]：半群S称为P-左可消，如果a，b，c∈S，(ca，cb)∈P，那么(a，b)∈P。显然左可消半群都是P-左可消半群。

定义6[8]：设A，B，C为半群，φ：A→C，ψ：B→C分别为A到C，B到C的半群同态映射，C是A，B的共同的同态像，并且S=[C；A，B；φ，ψ]={(a，b)∈A×B|aφ=bψ}，称S为A与B关于C，φ，ψ的织积。

1.2 基本理论

引理1[5]：(i)S的子半群满足置换恒等式；

(ii)E(S)是正规带；

(iii) 关于S的子半群T有A**(S)|T⊆A**(T)；

(iv) 关于a，b∈S有ab=aa+b=ab+b=aba+b+=a+b+ab。

引理2[5]：设S是满足置换恒等式的强wrpp半群。对于任意的a，b∈S，有(ab)+=a+b+。

引理3[6]：设S是满足置换恒等式的强wrpp半群。对于任意的e∈E(S)，Se是一个交换P-左可消幺半群。

引理4[6]：设S是满足置换恒等式的强wrpp半群，则下列条件是等价的：

(i)E(S)是矩形带；

(ii)S是A**-单的；

(iii)S是交换P-左可消幺半群与矩形带的直积。

2 主要结果

引理5：ρ={(a，b)∈S×S|a+εb+}为S上的半格同余，且每个ρ-类都是A**-单的满足置换恒等式的强wrpp半群。

证明：由引理1.2.2可知σ={(a，b)∈S×S|a+=b+}为S上一个同余，而且使得S/σ≌E(S)。设ε1为S/σ上的最小半格同余，则下图可换：

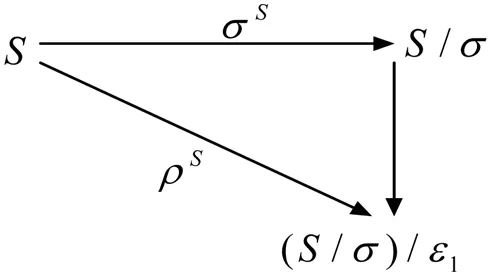
图1 最小半格同余的传递关系

因此ρ是S上的半格同余，设M为一个ρ-类，则E(M)为矩形带，且M=∪e∈E(M)Se，由引理3可知Se是一个交换P-左可消幺半群。对于任意的a∈M，由引理1(iii)得aA**(M)a+。如果e∈E(M)满足eA**(M)a使得ea=ae=a，则有ea+=(ea)+=a+，且由eA**(M)a+有ea+=e，因而e=a+。所以M是满足置换恒等式的强wrpp半群，由引理4可知M是A**-单的。

定理1：设S为一个半群，则下列条件等价：

(i)S是满足置换恒等式的强wrpp半群；

(ii)S是交换P-左可消幺半群与矩形带的直积的强半格；

(iii)S是交换P-左可消幺半群的强半格与正规带的织积；

(iv)S是强wrpp半群，且满足置换恒等式x1x2x3x4=x1x3x2x4。

证明：(i)⟹(ii)

设S是满足置换恒等式的强wrpp半群。ρ如引理5所定义，令Y=S/ρ，{Sα|α∈Y}为全体ρ-类的集合，则S是关于Sα(α∈Y)的强半格，由引理4，Sα是交换P-左可消幺半群与矩形带的直积。设E(S)的结构分解为[Y；Eα(α∈Y)；φα,β]，对于任意的α，β∈Y，并且α≥β，定义映射

由引理1(iv)可知Ψα,β是同态映射，且Ψα,α=1Sα。对于任意的a∈Sα和b∈Sβ(α，β∈Y)有

ab=aa+b+a+·b+bb+a+b+

=aa+b+a+·bb+a+b+

=a·a+φα,αβ·b+φβ,αβ·a+φα,αβ·b·b+φβ,αβ·a+φα,αβ·b+φβ,αβ

=(a·a+φα,αβ)· (b·b+φβ,αβ)

=aΨα,αβ·bΨβ,αβ

(ii)⟹(iii)

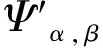
并且使得

当然半群T，E有共同的同态像，即半格Y。如果给定tα=αψ′，eα=αψ″，那么由这些(tα，eα)对组成T与E的织积，即

[Y；T，E；ψ′，ψ″]={(tα，eα)∈Tα×Eα|tαψ′=eαψ″}

织积中的乘法如下定义：

对于任意的(tα，eα)∈Tα×Eα，(tβ，eβ)∈Tβ×Eβ，有

(tα，eα) (tβ，eβ)= (tα°tβ，eα*eβ)

=(tα，eα)Ψα,αβ·(tβ，eβ)Ψβ,αβ

因此与S中的乘法是一致的。

(iii)⟹(iv)

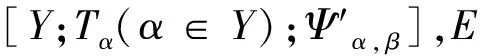
对于任意的x1，x2，x3，x4∈S，则存在(i，e) ∈Tα×Eα，(s，f) ∈Tβ×Eβ，(t，g) ∈Tγ×Eγ，(j，h) ∈Tδ×Eδ，使得x1=(i，e)，x2=(s，f)，x3=(t，g)，x4=(j，h)，取τ=αβγδ，则有

x1x2x3x4=(i，e)(s，f)(t，g)(j，h)

=(i，e)Ψα,τ·(s，f)Ψβ,τ·(t，g)Ψγ,τ·(j，h)Ψδ,τ

=(i，e)Ψα,τ·(t，g)Ψβ,τ·(s，f)Ψγ,τ·(j，h)Ψδ,τ

=(i，e)(s，f)(t，g)(j，h)

=x1x3x2x4

接下来证明S是强wrpp半群。设eA**fA**a，e∈E(Sβ)，f∈E(Sγ)，a∈Sα，且ea=ae=a，fa=af=a，则有e=ef，fe=f。对于任意的x∈Sλ，y∈Sμ，x+∈E(Si)，y+∈E(Sj)，取iβγ=δ，jβγ=t，则有

xe=ye⟺xef=yef

⟺xx+ef=yy+ef

⟺xx+f=yy+f

⟺xf=yf

因而eP*f，所以有ef=f，因此e=ef=f，即e=f。

(iv)⟹(i)是显然的。

3 结语

通过对wrpp半群引入可置换性，定义了满足置换恒等式的强wrpp半群。通过建立半群S上的一个半格同余ρ，得到了满足置换恒等式的强wrpp半群的结构，即满足置换恒等式的强wrpp半群是交换P-左可消幺半群与矩形带的直积的强半格及其等价条件，并给出了严格的证明。

[参考文献]

[1] Yamada M. Regular semigroups whose idempotents satisfy permutation identities[J]. Pacific J Math, 1967，21:371-397.

[2] X.J. Guo, Abundant semigroups whose idempotents satisfy permutation identities[J]. Semigroup Forum,1997,54:317-326.

[3] X.J. Guo, Structures of PI-strong rpp semigroups[J]. Kexue Tongbao (Chinese),1996,41:1647-1650.

[4] TANG X D. On a theorem of C-wrpp semigroups[J]. Comm. Algebra, 1997,25: 1449-1504.

[5] 任秀, 姜秀燕.满足置换恒等式的强wrpp半群的性质[J]. 大庆师范学院学报,2006(2): 25-27.

[6] 任秀，姜秀燕，孙凤芝. 满足置换恒等式的强wrpp半群的性质和特征[J]. 长春师范学院学报：自然科学版,2007(3):7-9.

[7] DU L, SHUM K P. On left C-wrpp semigroups[J].Semigroup Forum,2003,67 :373-387.

[8] J.M. Howie, Fundamentals of Semigroup Theory[M]. London :Academic Press,1995.