计及互感的开关磁阻电机单双相励磁静态性能分析

高洁， 孙鹤旭， 米彦青， 董砚， 何林

(1．河北工业大学控制科学与工程学院，天津 300130;2．天津清源电动车辆有限责任公司，天津 300450;3．天津职业技术师范大学自动化与电气工程学院，天津 300222)

0 引言

开关磁阻(switched reluctance，SR)电机的结构和工作原理比较简单，但其特有的双凸极结构定转子齿交叠前产生的边缘磁通引起电流非线性变化;并且开关电源供电使得转矩是由一系列脉冲转矩叠加而成，合成转矩亦非恒定值。这导致SR电机存在固有的转矩脉动，尤其电机低速运行时转矩脉动较大［1］，转矩脉动抑制的研究是近年来SR电机研究领域的热点之一，国内外学者从电机结构、电流优化控制等方面做了大量卓有成效的工作［2－3］。

为了减小转矩脉动，保持各相导通时电感曲线相互重叠是研究者所期望的，因而各相间的交互是不可避免的，一般SR电机的各相磁链和转矩分别计算，且通常忽略互感［1］。各相间的交互可归为两类:互感耦合及饱和效应。其中互感耦合是由于各相磁链交链引起的，而互感饱和则是下一相励磁时对前一导通相在其饱和区所产生的影响，饱和进而影响了磁链和输出转矩。通常情况下，SR电机的设计准则之一就是互感尽可能小，可以使得各相单独控制。然而大多数SR电机即使单相励磁时也工作在磁饱和区域，此时本身互感效应就已不能忽略，且下一相励磁过程中与前一相交链的磁路部分也将影响其饱和程度。

已有的文献［4－7］通常只是考虑了互感耦合效应，而往往忽略了互感的饱和。本文从电机设计的角度分析互感饱和的影响，利用有限元法详细分析相邻相对导通相磁链的影响，以及互感对输出转矩的影响。随着相数的增加，SR电机运行时的重叠区域也变得更大，由于四相8/6结构磁路的非对称性，本文将对此结构重点分析。

1 SR电机互感耦合分析

1.1 SR电机单相励磁模式互感耦合分析

互感的一般定义式为

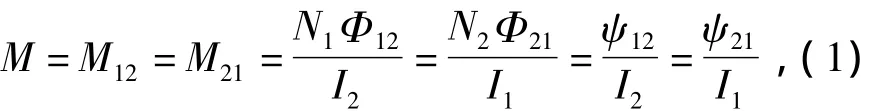
式中:N1、N2分别是线圈 1、2 的匝数;Φ12和 ψ12分别是线圈2中的电流I2在线圈1中产生的每匝磁通量和磁链，Φ21和ψ21分别是线圈1中的电流I1在线圈2中产生的每匝磁通量和磁链。

互感系数的大小取决于两个线圈的几何形状，大小，相对位置，各自的匝数以及它们周围介质的磁导率。在SR电机中，各相绕组的几何形状、大小、相对位置及匝数都是固定的。但是线圈之间是通过转子耦合的，当转子转动时各相线圈间的磁阻发生着周期性的变化，此周期和转子的极数相关。

下面对SR电机单相励磁情况进行有限元分析，各相依次通入7 A的方波电流，每相导通15°，通电周期为一个转子极距60°，SR电机绕组采用NSNSSNSN排列方式，其自感和互感曲线如图1所示，AB、BC、CD相邻相均为短磁路连接，极性相反，导通相磁力线与其相邻相的磁场方向一致，互感磁链具有加强相邻相磁场的作用，因此其互感均为正值;而DA相为长磁路连接，两相极性相同，导通相A的磁力线与相邻相D的磁场方向相反，互感磁链则会减弱D相的磁链，因此互感为负。

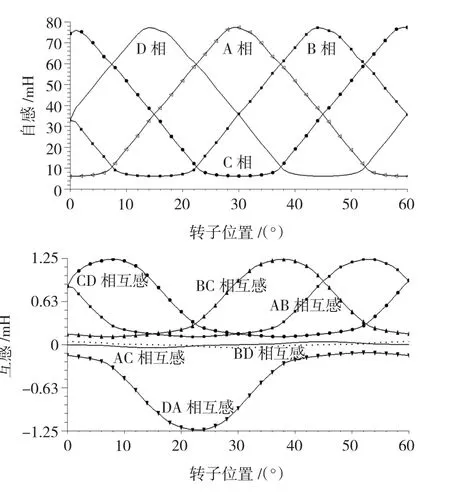
图1 NSNSSNSN连接方式时单相励磁各相自感和互感特性曲线Fig．1 The self and mutual inductance of single phase excitation with NSNSSNSN connection

同样地，如图2所示，SR电机为NNNNSSSS时，AB、BC、CD相邻相均为长磁路连接，其互感均为负值，而DA两相为短磁路连接，其互感值则为正。且对齐位置自感值近似为非对齐位置的12.5倍，这就为控制相电流和磁链带来了难度。相邻相的互感不超过与之相关自感值的6.4%，而非相邻相的互感则不超过0.07%，因此，尽管在文献［8］中非相邻相的互感用于在无位置控制中检测转子位置，但是其他情况下该互感基本可以忽略。

图2 NNNNSSSS连接时单相励磁各相自感和互感特性曲线Fig．2 The self and mutual inductance of single phase excitation with NNNNSSSS connection

1.2 SR电机双相励磁模式互感耦合分析

与SR电机单相励磁类似，两相同时导通的互感也不仅仅是各自单相导通的线性叠加，如图3所示。对各相依次通入7A方波电流，每相导通30°，通电周期亦为60°。两相同时励磁对于减小转矩脉动和降低相电流都是有利的，但是互感耦合不可忽略。这也是高性能SR电机控制研究互感耦合效应的重要性。

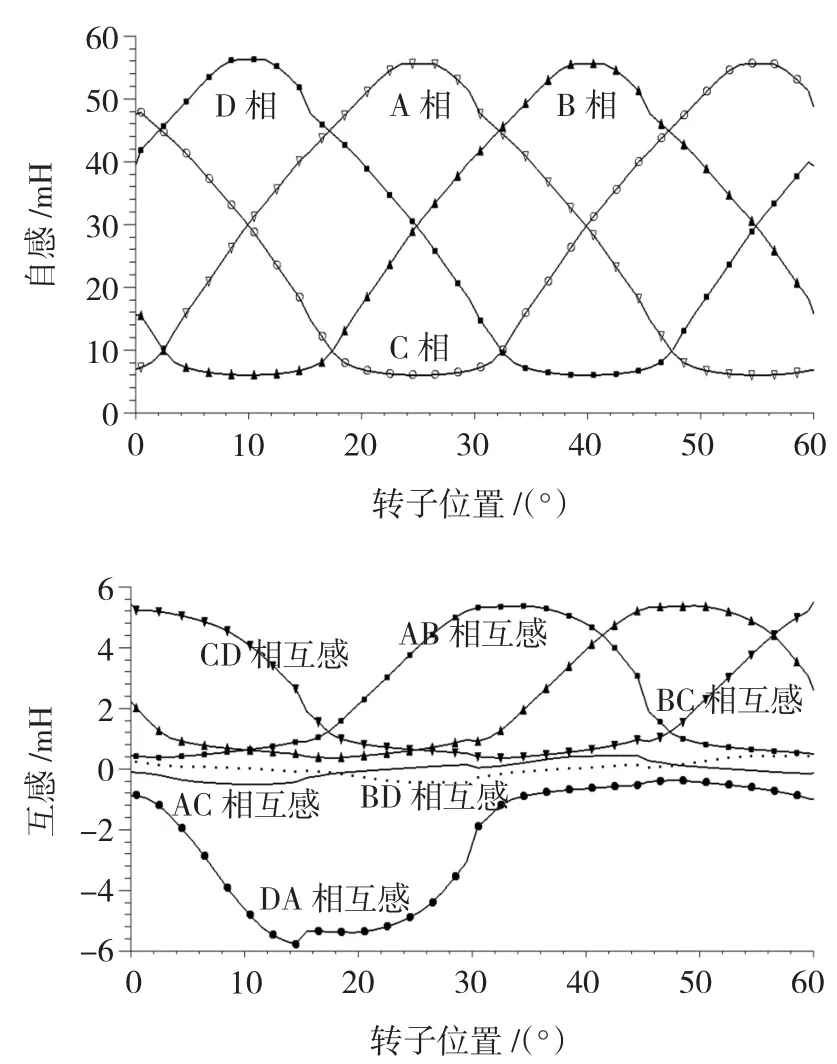
图3 NSNSSNSN连接方式时两相励磁自感和互感特性曲线Fig．3 The self and mutual inductance of double phase excitation with NSNSSNSN connection

进一步对两相励磁模式不同电流下长、短磁路的自感和互感进行分析，如图4所示，DA相长磁路励磁互感均为负值，这是由于DA相间的磁路较长，而轭部的磁饱和使得DA间的互感磁链沿不饱和的DA相间的轭部穿过两相线圈。在短磁路模式下，当励磁电流较大时，由于磁饱和的原因使得DA相间较短轭部的磁阻增大，互感磁链沿着较长但是磁阻较小的轭部穿过DA相，所以互感也为负值。当电流较小时，短轭部的磁阻小于长轭部，互感磁链会先择较小的短轭部磁路闭合，所以此时互感值为正。

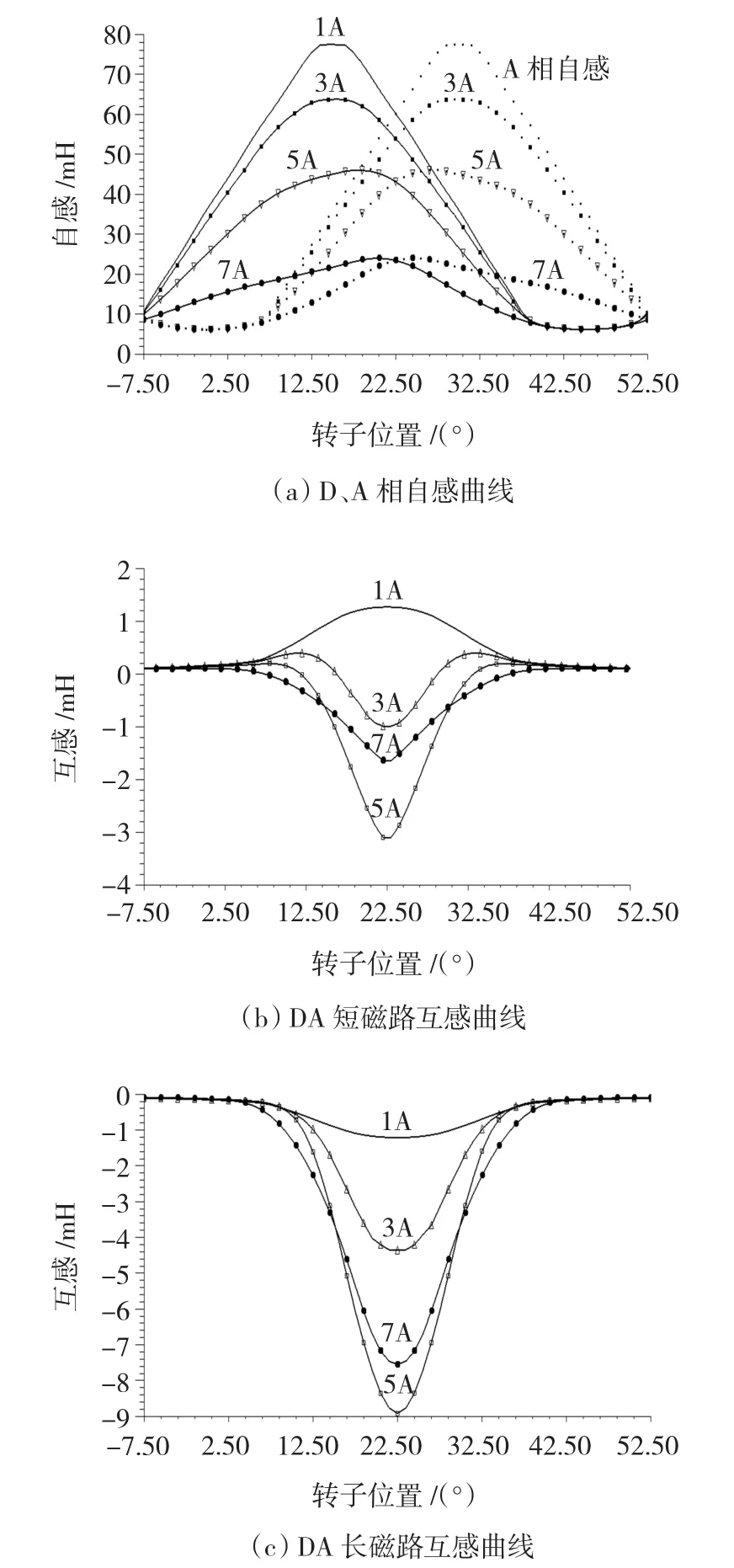
图4 两相励磁模式下不同电流对应的自感与互感曲线Fig．4 The self and mutual inductance of double phase excitation corresponding to different currents

同时从图4可知，在相同的转子位置和较大的励磁电流情况下，长磁路互感的绝对值比短磁路要大，这是由于在长磁路模式下互感磁链闭合路径的磁阻要小于短磁路模式。而电流较小时，两个互感磁链闭合路径的磁阻相差不大，所以互感绝对值相差不大。

从图4中还可以看出，当转子转到22.5°时，即DA两相和转子极的重合面积相等时，DA相间互感达到最大，相间磁阻最小。当转子转到－7.5°或52.5°位置时，即转子极和DA相间的定子槽对齐位置时，DA两相和转子均无重合，此时DA相间磁阻最大，互感达到最小值，两互感曲线关于22.5°位置轴对称。

2 SR电机互感饱和分析

2.1 SR电机单双相励磁磁力线分布

相绕组间互感的饱和效应，其机理与自感相同，只是主要考虑两相绕组互感磁路饱和度的变化，而不是某一相绕组磁路。首先，定义定转子齿槽对齐位置为0°，定转子齿齿对齐位置为30°，电机逆时针转动，A相为导通相，D相为其前置相，B相为滞后相，四相8/6极SR电机导通角为15°，单相导通时如图5(a)中。若导通角小于15°，相电流不会相互重合，但是为了减小转矩脉动，通常使得相邻相电流要有一定的重叠区域，如图5(b)所示为DA两相长磁路模式，除了两相间定子轭部磁链方向相反外，其余定子轭部的磁链方向都相同。即使只有一相导通，定子轭部在某个转子位置时也有部分饱和，特别是位于对齐位置处。类似地，图5(c)为DA两相短磁路模式，除了DA两相间定子轭部磁链方向相同外，其余定子轭部磁链方向都相反，也即其余部分的磁阻减小。

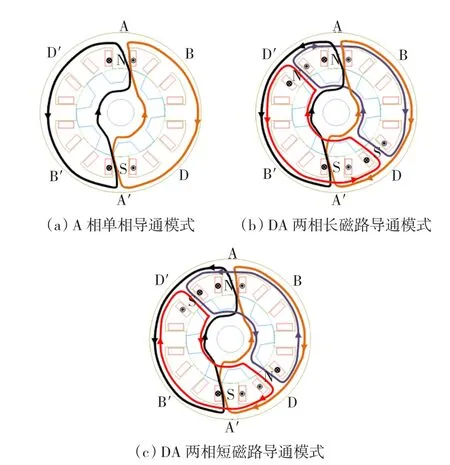
图5 导通相磁路曲线Fig．5 Leading phase influence on flux

图6(a)所示为A相励磁的磁场分布图，转子位置角为15°，单相励磁时，定子轭部的磁力线被对称均分，其磁密近似相等。图6(b)所示为DA两相长磁路模式导通，此时D相处于齿齿对齐位置，A相仍处于15°位置，此时相当于励磁电流关断位置。由于两相绕组同时励磁时，相间磁场相互耦合，定转子轭部磁通量大幅增加，磁场的饱和程度和分布情况也与单相励磁磁场有较大区别。图6(c)所示为DA两相在短磁路模式导通的磁场分布图，DA两相之间的定子轭部磁场高度饱和。因此为了减小饱和效应和降低铜耗，SR电机应采用短磁路连接，同时亦可以增大输出转矩。

图6 导通相磁力线有限元分析图Fig．6 Finite-element plots of flux lines for the excitation phases

由图5、图6可知，当SR电机单相励磁处于齿槽对齐位置时，气隙磁阻较大，漏磁通也较大。当定转子极部分重合时，其极身的局部饱和最为严重。随着重合面积增大，定、转子极身的局部饱和度将逐渐减小，完全重合时，除极尖部分外，其它部分基本上不饱和。DA两相励磁和单相励磁的磁场分布及饱和程度均有较大差别，主要体现在轭部磁路上。以D相为例，单相励磁时定转子轭部磁通约为齿部的一半，而DA两相同时励磁时，定转子轭部和齿部磁通基本相等。因此两相励磁时轭部磁势降因磁路过饱和而大幅增加，将导致每相磁通减小，从而每相磁链减小。

2.2 SR电机两相励磁模式互感饱和分析

下面分析两相励磁时互感饱和的影响，对于导通相A而言，同时给D相或B相输入恒定等值电流计算磁链。如图7所示，实线为A相在0～30°范围内励磁磁链曲线;左箭头虚线表示DA两相在0～15°范围内同时励磁的A相磁链曲线，即两相长磁路连接方式;下三角虚线代表AB两相在15～30°范围内同时励磁的A相磁链曲线，也即短磁路连接方式。由图7可知，相电流在0到2 A范围内，磁场尚未饱和，磁链与励磁电流为线性关系，磁链线性叠加，3种励磁方式下的磁链特性基本重叠;当相电流大于2 A时，磁场开始饱和，且单相励磁时定转子轭部磁通密度比两相励磁小，饱和程度低，磁势降亦小，因此相电流相同时磁链相对较大;而两相励磁时，长磁路励磁模式下定、转子轭部路径长度分别是短磁路励磁方式的3倍和2倍，轭部具有更大的磁势降;所以长磁路励磁模式各相磁链最小，短磁路次之，单相励磁时最大。

进一步分析不同转子位置的磁链变化:首先从非对齐位置到15°之前范围内分析，当A相位于定转子齿槽对齐位置时，单相导通的磁链值最小;在此区间内，D相定、转子还未到达齿齿对齐位置，因而其磁链未达到峰值，且D相若是处于非对齐位置区间内，其对A相的影响很小。然而，当A相处于15°时，由于定转子极重合面积增大，其自身磁链值增大，此时D相处于齿齿对齐位置，磁链达到峰值，互感饱和也在此点增强。转子处于15°位置时，B相开始导通且处于齿槽对齐位置，而D相处于齿齿对齐且励磁电流关断状态。当转子逐渐转至30°，A相处于齿齿对齐位置，此时，定子轭部的磁链将由D相对其影响较大状态过渡到B相的影响较小状态，图7同时也表明了转子转到15°时磁链产生跃变，这是因为此位置D相处于完全对齐并且磁链最大，接着D相关断，B相开始导通，此时B相处于非对齐位置且磁链最小，与D相相比，B相在15°的影响可以忽略。B相对A相磁链的影响随着其达到齿齿对齐位置而增强，两相磁链同时增加，此时已不可忽略。

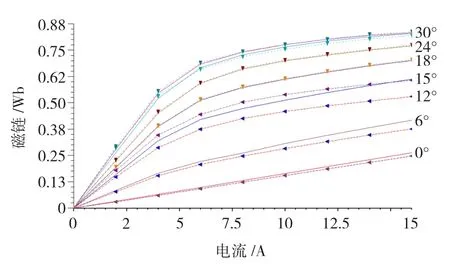
图7 单双相励磁磁链曲线Fig．7 The flux lines of both single and double phase excitation

因此当SR电机处于两相励磁模式时，若采用单相励磁获取的磁链计算电机的磁共能进而求得输出转矩，将产生较大误差，尤其当相邻两相为长磁路励磁模式时。为准确地反映两相励磁时由于相间耦合、磁场分布以及饱和导致的磁链与单相励磁的差别，必须考虑互感饱和及耦合的影响。

3 SR电机互感特性的实验研究

为了验证上述模型的正确性，本文利用数字电桥来测量各相的电感值和各相间的互感值。常用的互感的测量方法有:磁通法、伏安法、串联法等［9－10］。本文采用的串联法，这种方法电路连接简单，读数方便。

两个具有互感的线圈若是异名端相连则为顺向串联，若是同名端相连则为反向串联。顺向串联有

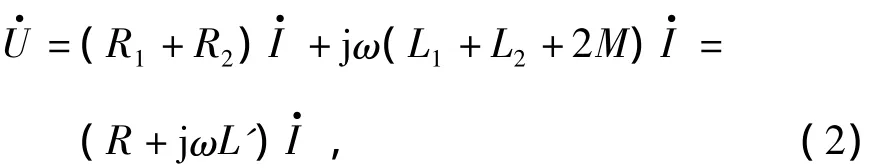
式中:R为两线圈的等效电阻;L为顺向串联的等效电感，且有L=［(U/I)2－R2］0.5/ω。

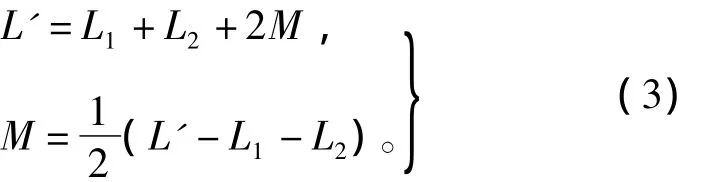
反向串联有

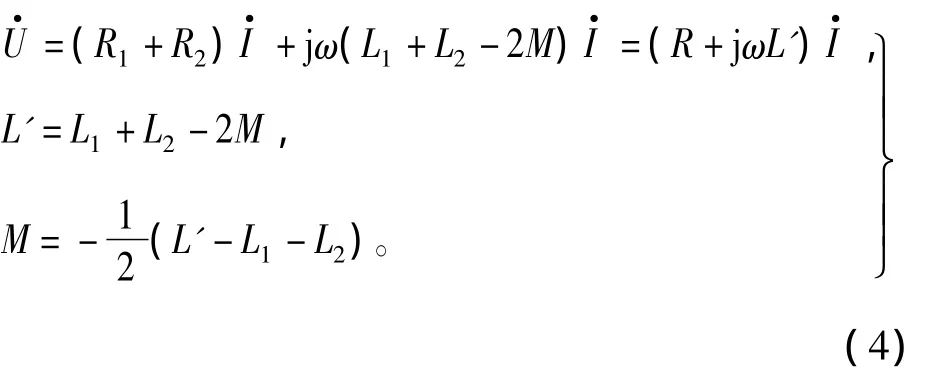
对四相8/6结构的SR电机进行测试，测量时DA两相是顺向串联，其它相均为反向串联。测试时让电机轴的中心和万能分度头的轴心处于同一个水平位置。使万能分度头带动电机轴转动，万能分度头的蜗轮、蜗杆的减速率为40∶1，而分度盘最外圈的孔数为66个，所以手柄每转过一个孔，电机转动0.136°。实验中万能分度头的手柄每转过10个孔，即电机轴每转过1.36°则测一次电机四相，及两两串联的电感。测量电感的仪器采用的是同惠电子有限公司的TH2817A数字电桥，测试环境为数字电桥输出2 V、5 kHz的交流信号，先测量每一相的自感，再测两相串联的等效电感，再利用式(3)和式(4)计算出互感M，图8为被测样机 A、B、C、D 四相的自感曲线，以及 AB、AC、DA相间互感曲线，实验结果与有限元分析结果趋势一致，稍有误差。

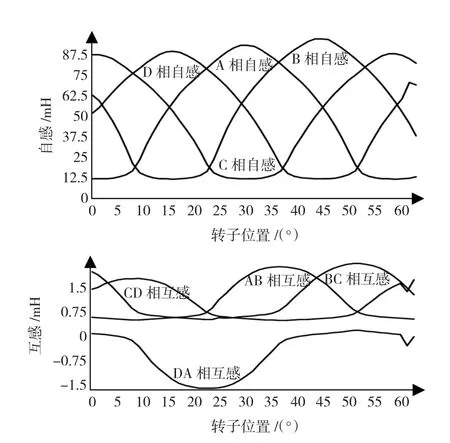
图8 SR电机单相励磁实测自感和互感曲线Fig．8 The self and mutual inductance test results with single phase excitation

4 SR电机互感及其对矩角特性的影响

为定性分析互感对矩角特性的影响，假设任意相邻两相绕组导通时，其余相电流为零且磁通为零;并有每相漏磁通为零［11－12］。利用有限元计算 SR电机分别在D相励磁，A相励磁，DA两相短磁路励磁以及长磁路励磁方式下，如图2所示位置的矩角特性，计算结果如图9所示，其中TA代表A相单相励磁转矩，TD代表D相单相励磁转矩，TADS为相邻两相短磁路励磁模式下的总转矩;TADL为长磁路励磁方式下的总转矩，Tsum代表D、A两相分别单相励磁时转矩的代数和。

图9(a)是DA两相绕组电流均为1 A时的矩角特性，对比DA两相短磁路励磁、长磁路励磁时的输出转矩和分别单相励磁时的转矩和，可以看出三条曲线非常接近，但略有差别。这是由于励磁电流为1 A时，磁场不饱和，磁场强度大小与励磁电流尚为线性关系。由于励磁电流为1 A时，短磁路互感为正，而长磁路互感为负，短磁路时输出转矩略大，分别单相励磁时的转矩和次之，长磁路最小。图9(b)、(c)、(d)分别是 DA 相绕组电流为 3 A、5 A、7 A时的矩角特性。

转子位置在0～8°区间内，长、短磁路的互感值都很小，绕组电流一定时，长、短磁路的磁共能与分别单相励磁时两相的代数和基本相等，因此DA两相短磁路、长磁路励磁时的矩角特性曲线以及分别单相励磁时的转矩之和曲线基本重叠。

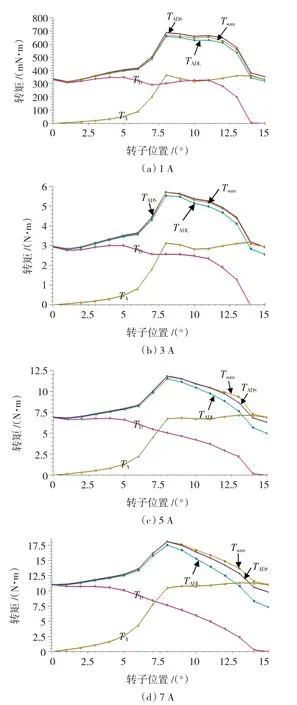
图9 SR电机不同励磁模式下的静态转矩对比曲线Fig．9 The contrast curves of the static torque for different excitation modes

转子位置在8～15°区间内，随着角度的增加，三条曲线的差别也越来越大。这是由于转子位置越靠近15°，长、短磁路互感的绝对值越大，不同励磁模式磁共能变化量的差别就越大，转矩差别也就越大。图9表明绕组电流较大时，长、短磁路励磁模式下的互感均为负，且长磁路负互感的绝对值大于短磁路负互感的绝对值。两相分别单相励磁时的转矩之和最大，短磁路时的输出转矩次之，长磁路最小。因此，有限元计算结果与理论分析结果相一致。

为了对结论进行进一步验证，本文实测了SR样机在额定电流下长、短磁路的转矩，如图10所示。理论分析和有限元计算以及实验结果均表明，相邻两相为短磁路励磁模式时，可获取较高平均转矩。

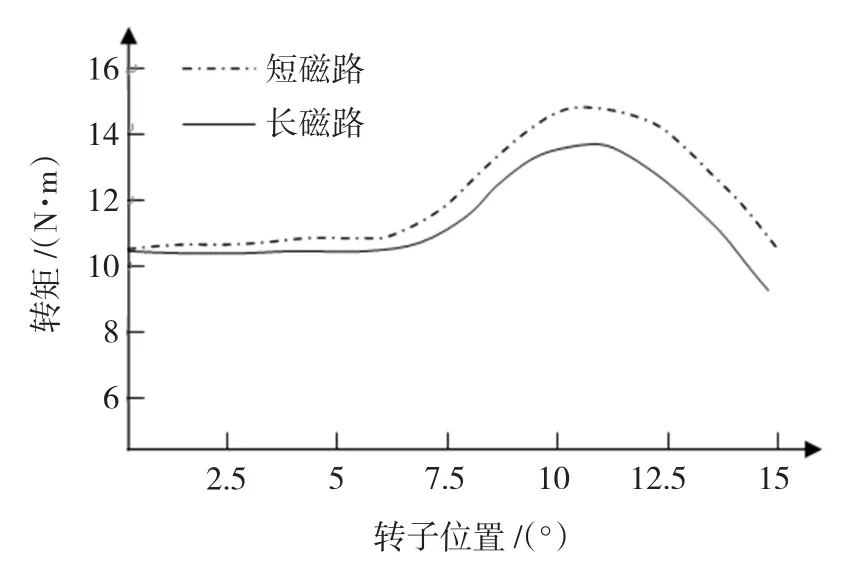
图10 SR电机长短磁路实测转矩曲线(i=7 A)Fig．10 The curves of the static torque for different magnetic circuits(i=7 A)

5 结语

本文以四相8/6结构SR电机为研究对象，用有限元法详细分析了SR电机长、短磁路模式下单双相励磁的静态性能。包括自感和互感曲线随相电流及转子位置的变化规律，并通过实验方法进行了验证与计算，得出当SR电机两相励磁模式时，若采用单相励磁获取的磁链计算电机磁共能求得输出转矩，将产生较大误差，尤其当相邻两相为长磁路励磁模式时。同时分析了相邻相对导通相磁链的影响，以及长、短磁路模式下一个步进角内的平均转矩，且短磁路模式下能够获得更高的平均转矩。本文分析表明:为准确反映两相励磁时由于相间耦合、磁场分布以及饱和导致的磁链与单相励磁的差别，必须考虑互感饱和及耦合的影响，为SR电机数学建模及其高性能控制提供了依据。

［1］MILLER T J E．Switched Reluctance Motors and Their Control［M］．Oxford:Clarendon，1993:7－24．

［2］LI G J，OJEDA J，HLIOUI S，et al．Modification in rotor pole geometry of mutually coupled switched reluctance machine for torque ripple mitigating ［J］．IEEE Transactions on Magnetics，2012，48(6):2025 －2034．

［3］张慧英，汪旭东，高彩霞．减小开关磁阻电机转矩脉动、噪声和振动方法研究综述［J］．微电机，2009，42(8):65－68．

ZHANG Huiying，WANG Xudong，GAO Caixia．Study of optimization design methods of switched reluctance motor［J］．Micromotor，2009，42(8):65 －68．

［4］PRESTON M A，LYONS J P．A switched reluctance motor model with mutual coupling and multi-phase excitation［J］．IEEE Transactions on Magnetics，1991，27(6):5423 －5425．

［5］MICHAELIDES A M，POLLOCK C．Modeling and design of switched reluctance motors with two phase simultaneously excited［J］IEE Proceedings-Electric Power Applications，1996，143(5):361－370．

［6］PILLAY P，LIU Y，CAI W，et al．Multiphase operation of switched reluctance motor drives［C］//Thirty-Second IAS Annual Meeting-Industry Applications Conference，October 5 － 9，1997，New Orleans，USA．1997，1:310 －317．

［7］JAINA K，MOHAN N．Dynamic modeling，experimental characterization，and verification for SRM operation with simultaneous two-phase excitation［J］．IEEE Transactions on Industrial electronics，2006，53(4):1238 －1249．

［8］PANDA D，RAMANARAYANAN V．Mutual coupling and its effect on steady-state performance and position estimation of even and odd number phase switched reluctance motor drive［J］．IEEE Transactions on Magnetics，2007，43(8):3445 －3456．

［9］RADIMOV N，BEN-HAIL N，RABINOVICI R．Inductance measurements in switched reluctance machines［J］．IEEE Transactions on Magnetics，2005，41(4):1296 －1299．

［10］ZHANG Peng，CASSANI P A，WILLIAMSON S S．An accurate inductance profile measurement technique for switched reluctance machines［J］．IEEE Transactions on Industrial Electronics，2010，57(9):2972 －2979．

［11］曲兵妮，宋建成．开关磁阻电动机互感特性及其对转矩的影响［J］．电机与控制学报，2009，13(3):332 －336．

QU Bingni，SONG Jiancheng．Mutual inductance of switched reluctance motor and its effect on torque［J］．Electric Machine and Control，2009，13(3):332 －336．

［12］LIU YAGUANG，PILLAY P．Improved Torque performance of switched reluctance machines by reducing the mutual saturation effect［J］．IEEE Transactions on Energy Conversion，2004，19(2):251－257．