单级同步感应线圈炮场－路耦合分析与参数优化

邹本贵， 李瑞锋， 曹延杰， 单岳春， 王旻

(1．海军航空工程学院指挥系，山东烟台 264001;2．海军航空工程学院研究生管理大队，山东烟台 264001;3．信息工程大学 理学院，河南 郑州 450003)

0 引言

对于用电容器馈电的单级同步感应线圈炮(single－stage synchronous induction coilgun，SSICG)，往往已知的是端口电压的约束条件，很难预先得知驱动线圈中响应电流的分布规律［1－5］。在求解SSICG的瞬态涡流场问题时，通常是预先给出源电流区瞬态电流的分布规律再进行离散带入到场方程中求解，这种方法势必造成一定的误差。特别是进一步对磁场力进行计算时，误差会更大［6－9］。

为了准确地确定SSICG驱动线圈中的响应电流，建立了SSICG二维场－路耦合的数学模型;利用APDL编制了基于场－路耦合数学模型的仿真程序并从仿真与实验两方面验证了仿真程序的有效性;基于场－路耦合程序建立了SSICG回路参数优化数学模型，对回路中电路参数进行了优化，根据优化结果进行了发射实验。

1 SSICG二维场－路耦合数学模型

1.1 二维瞬态涡流场方程

SSICG发射系统是由单回路构成的，属于低频瞬态涡流场问题［10－11］。如图1所示，SSICG涡流场分析中既包含涡流区V3，也包含源电流区V2，二维平面场方程可以看作涡流区场方程和源区的场方程的联立［12－14］，即

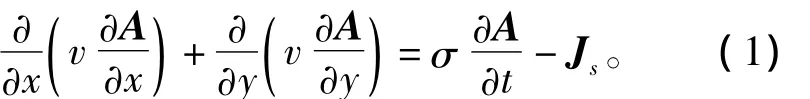
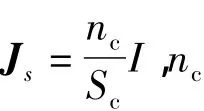
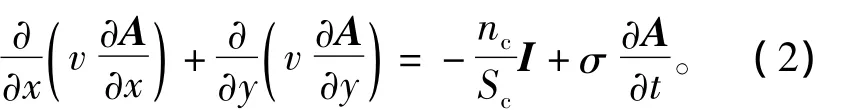
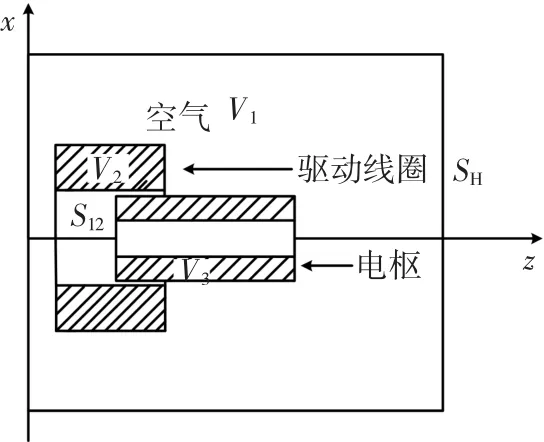
图1 涡流场求解区域Fig．1 Eddy current domain

利用加权余量法建立上述方程的空间离散方程，取权函数等于形状函数［N］T，式(2)的空间离散方程为

1.2 电路方程

SSICG耦合电路如图2所示，其电压方程为［15］

式中，u、i(t)分别为电容器的放电电压和回路中的响应电流，R和L为回路中的电阻和电感，e为驱动线圈的感应电动势。

图2 场－路耦合的等效电路模型Fig．2 Coupled field-circuit equivalent circuit model

导体内存在感应电流表明导体内必然存在感应电场Ein，因此，感应电动势可以表示为感应电场Ein的积分［16］，即

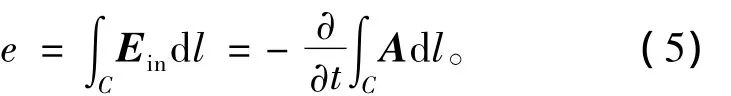
将式(5)带入式(4)，可得

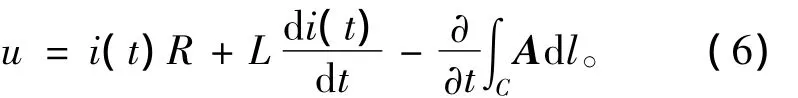
将式(6)写成矩阵形式为

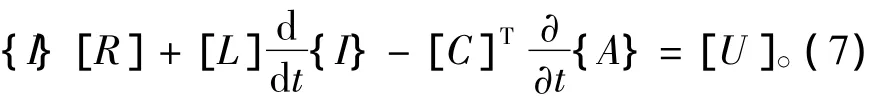
将式(3)和式(7)联立得

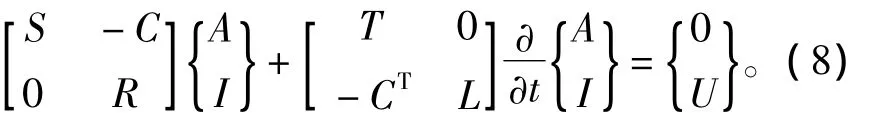
这样，电路方程和电磁场方程通过矢量磁位A和电流I耦合起来，形成了SSICG场路耦合的数学模型。

2 场－路耦合仿真分析

2.1 场－路耦合程序设计

APDL(ANSYS parametric design language)即ANSYS参数化设计语言，是ANSYS设计优化的基础［17］。根据SSICG二维场－路耦合的数学模型编制了仿真程序coilgun，对SSICG的放电过程进行了仿真分析，得出了电容器放电激励下回路电流。基于APDL的SSICG场－路耦合程序coilgun的设计流程如图3所示。

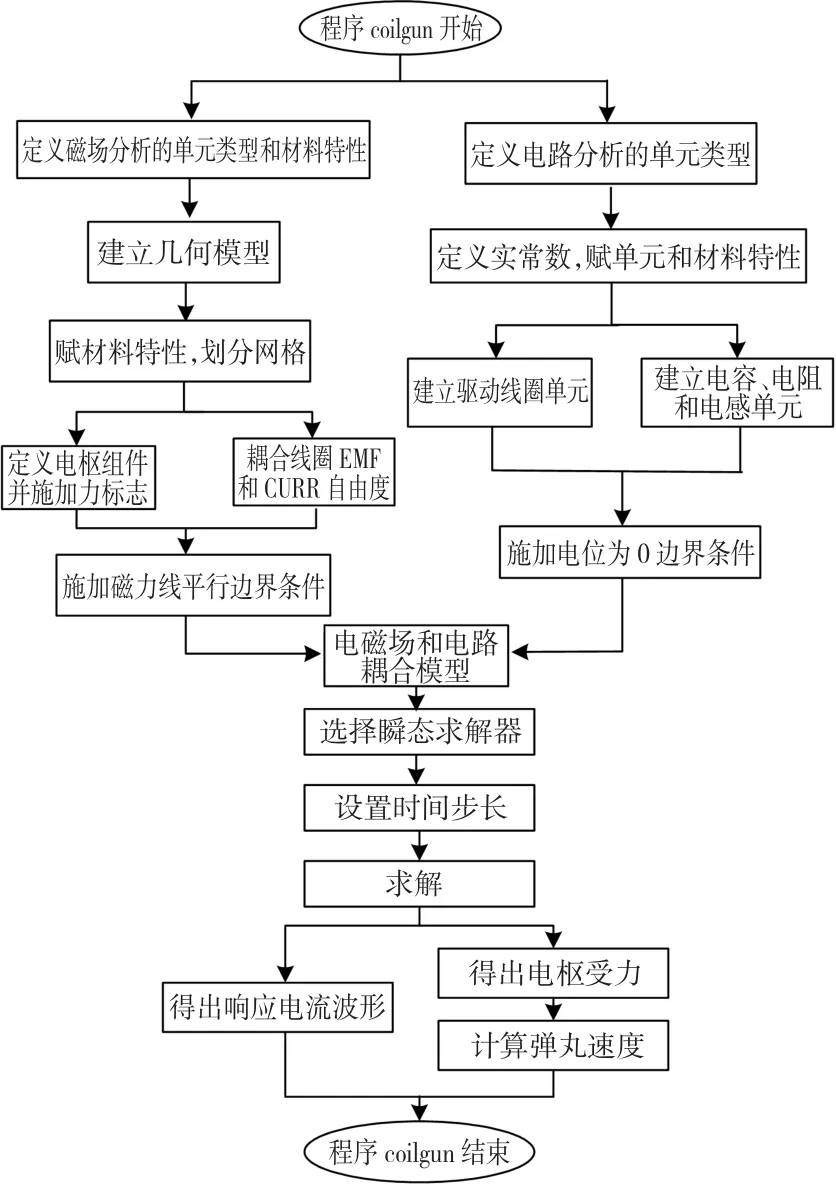
图3 耦合程序设计流程图Fig．3 Flow chart of coupled fields anlysis

2.2 场－路耦合有限元仿真

1)物理模型及参数

物理模型的结构参数和电路参数均来自于文献［18］。驱动线圈和电枢的结构剖面图如图4所示，结构参数如表1所示，电路参数如表2所示。

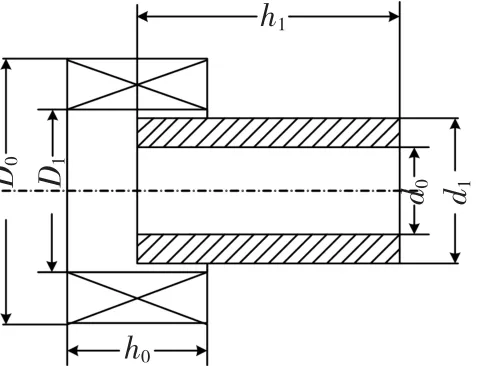
图4 驱动线圈和电枢的结构剖面图Fig．4 Structure drawing of drive coil and armature

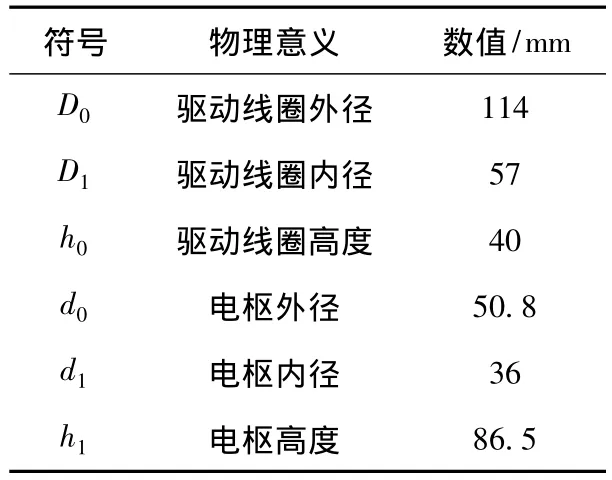
表1 驱动线圈和电枢的结构参数Table 1 Structure parameters of drive coil and armature

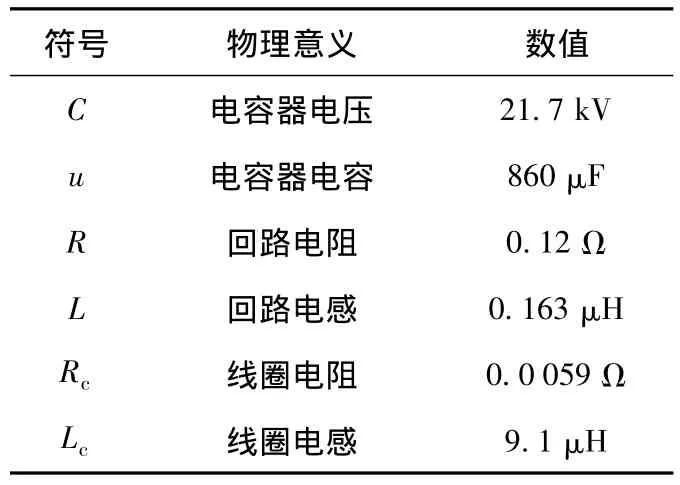
表2 放电回路的电路参数Table 2 Parameters of discharging loop

2)仿真结果

根据表1的结构参数和表2的电路参数，运行仿真程序coilgun得出电容器激励下驱动线圈中响应电流波形，如图5所示。

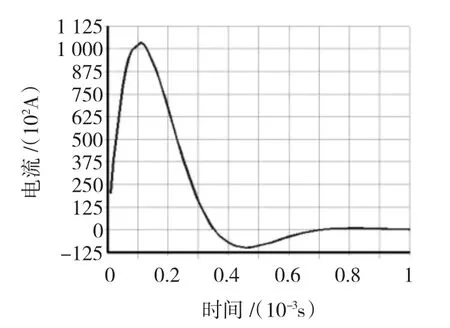
图5 回路中的响应电流Fig．5 Waveform of current in the loop

从图5看出，响应电流先迅速增大，而后迅速变小且存在阻尼振荡，最大电流在0.11 ms时达到103.50 kA，在0.35 ms时电流减小为0，反向电流在0.46 ms时最大为9.80 kA。

3 场－路耦合仿真程序验证

3.1 SLINGSHOT验证

SLINGSHOT是美国权威的感应型线圈炮设计程序，该程序可以计算驱动线圈中的响应电流以及电枢中感应的涡流、电枢的受力及电枢速度［19］。

根据表1的结构参数和表2的电路参数，SLINGSHOT仿真程序的仿真结果如图6所示［18］。

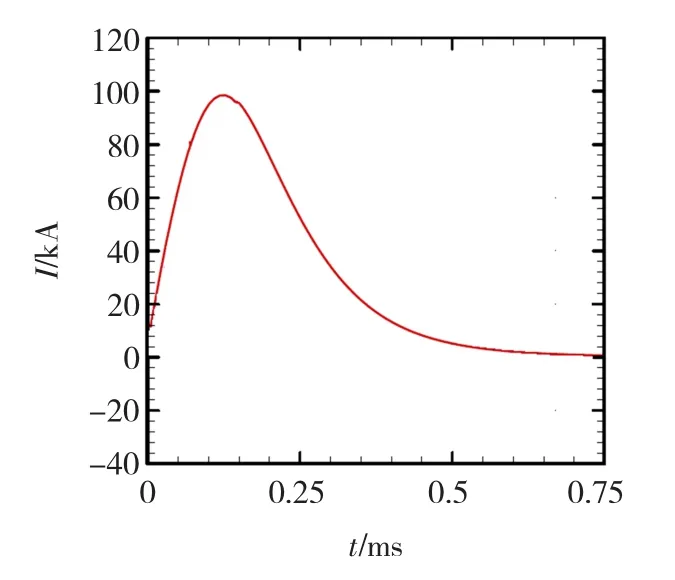
图6 SLINGSHOT仿真的电流波形Fig．6 Waveform of current simulated by SLINGSHOT

从图6看出，响应电流在0.125 ms时达到最大，最大值为100.00 kA。由于SLINGSHOT仿真程序考虑了前置电路的影响，消除了电路中的阻尼振荡，所以不会产生反向电流。

从图5和图6的比较可以得出，响应电流最大值的相对误差为

电流达到最大值时时间的相对误差为12.00%。

3.2 实验验证

为了进一步验证耦合程序coilgun的有效性，进行了SSICG发射实验且测量了回路中的响应电流，并与仿真结果进行了比较。

1)实验原理与初始参数

SSICG发射实验装置的结构原理如图7所示。基本工作原理为:首先对电容器充电，把电能储存在电容器中，然后电容器通过三电极间隙开关瞬间放电，驱动线圈产生瞬态强磁场，电枢中感应的涡流与磁场相互作用产生电磁力推动弹丸飞离炮口。

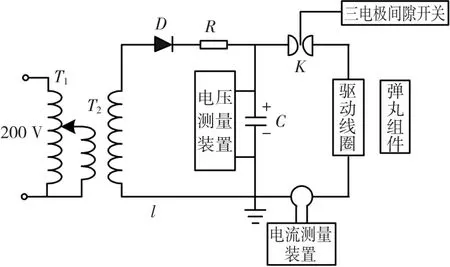
图7 实验装置结构原理图Fig．7 Structure principle of the experiment equipment

实验中驱动线圈和电枢的实物如图8所示，其结构参数如表3所示，外置电路参数如表4所示。

图8 驱动线圈和电枢Fig．8 Drive coil and armature

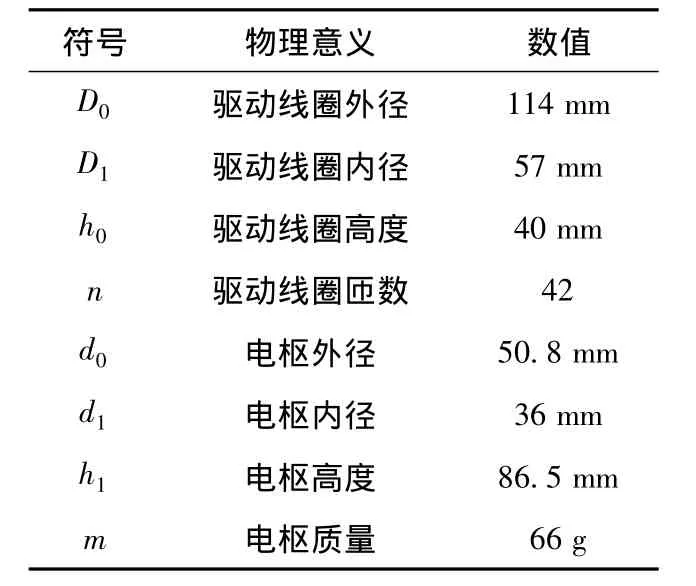
表3 驱动线圈和电枢的结构参数Table 3 Structure parameters of drive coil and armature

表4 外置电路参数Table 4 Parameters of discharging loop

2)回路电流的比较

实验中回路电流的测量采用自积分式Rogowski线圈法。充电电压为1 500 V时Rogowski线圈测得的感应电流波形如图9所示，仿真电流波形如图10所示。

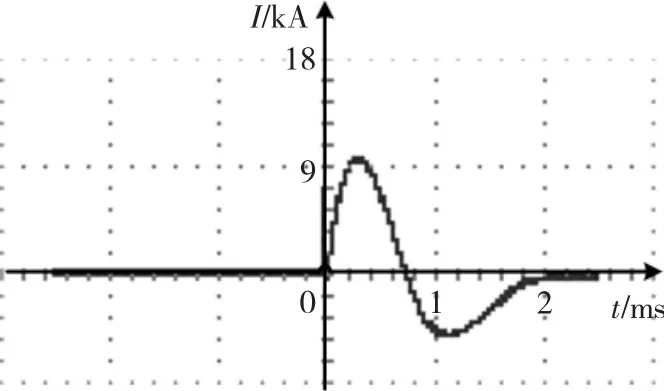
图9 测量的感应电流Fig．9 Inductive current in measurement

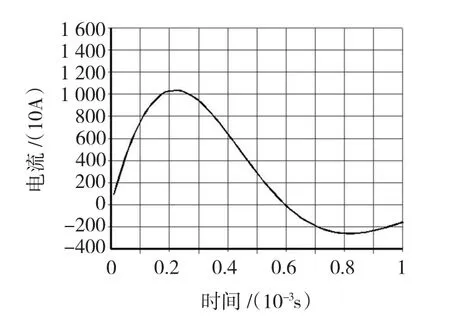
图10 仿真电流Fig．10 Simulated current

从图9看出，回路电流在0．25 ms时最大，最大电流为9.52 kA。从图10看出，回路电流在0.23 ms达到最大值10.36 kA，与实验数据的相对误差为8.80%。

仿真结果通过分别与SLINGSHOT和实验结果的比较可以得出SSICG场－路耦合程序coilgun是可行的。

4 基于场－路耦合的回路参数优化

场－路耦合程序可以准确的确定驱动线圈中的响应电流，以场－路耦合程序coilgun为基础，建立了SSICG回路参数优化数学模型。

求设计变量

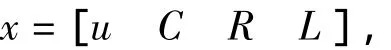
使目标函数

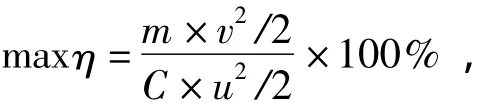
且满足约束条件

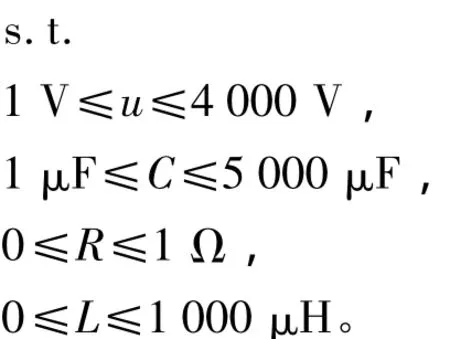
式中，u、C、R、L分别为电容器的放电电压、电容、回路总电阻和回路总电感;η为系统的发射效率。

设计变量的初值为

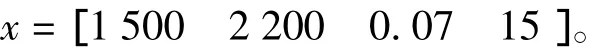
经过迭代计算，得出优化前后各参数对照如表5所示，电枢的速度曲线如图11所示。

从表5和图11可以看出，回路参数对系统发射效率具有较大影响，合理的改变回路参数可以有效地提高电枢速度和系统的发射效率。

根据优化后各参数的数值，进行了SSICG的发射实验。实验中采用网靶测速的方法来测量电枢的初速度，测速原理图如图12所示。

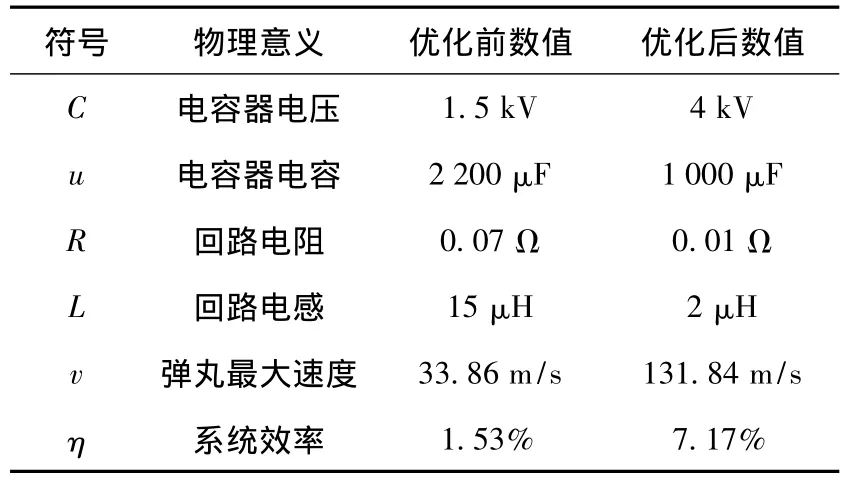
表5 优化前后仿真参数对照表Table 5 Simulation parameters of before and after optimization

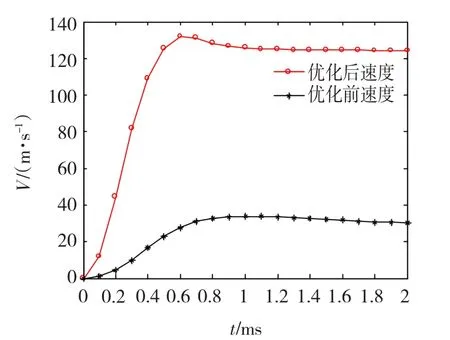
图11 优化前后电枢的速度Fig．11 Velocity of the armature before and after optimization

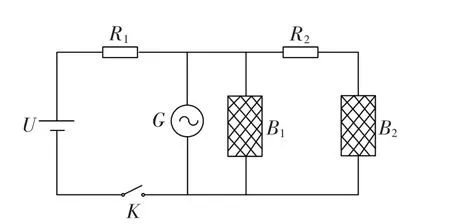
图12 测速原理图Fig．12 Principle chart of measuring velocity

当电枢穿过测速区域，撞断网靶1两端的铜丝，示波器在t1时刻采集R2两端电压U/2，t2时刻网靶2被撞断，示波器开始采集电源电压U，时间间隔Δt=t2－t1即为电枢在测速区域运行的时间。两网靶间的距离为l，则电枢的初速度为

实验中网靶距离l=350 mm，优化前后电枢通过两网靶时示波器测量的电压信号如图13和图14所示。

从图13和图14看出，优化前后电枢穿过两网靶的时间间隔分别为12 ms和5 ms，优化前后电枢的速度由29.17 m/s提高到70 m/s，系统的发射效率由1.14%提高到2.02%。

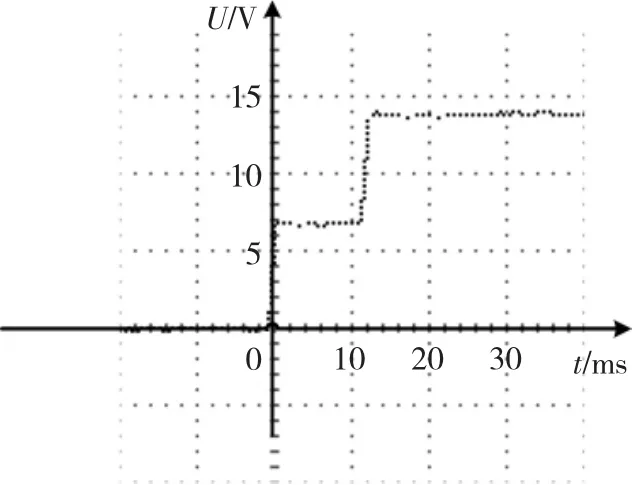
图13 优化前网靶电压信号Fig．13 Voltage signal of net target before optimization

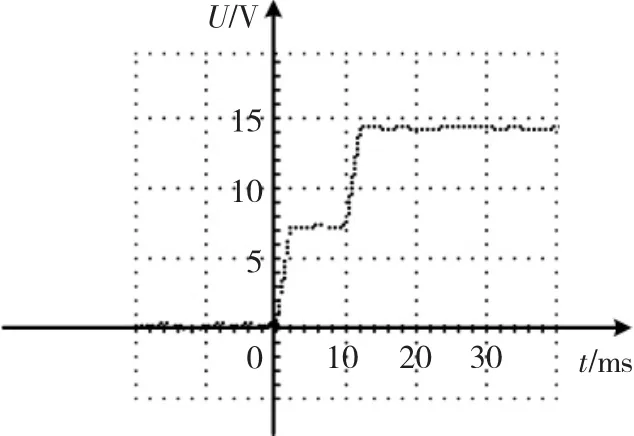
图14 优化后网靶电压信号Fig．14 Voltage signal of net target after optimization

5 结语

文中建立了SSICG二维场－路耦合的数学模型，利用APDL编制场－路耦合的仿真程序，通过SLINGSHOT和实验验证了程序的有效性，基于场－路耦合程序建立了SSICG回路参数优化数学模型并对SSICG回路参数进行了优化，根据优化结果进行了发射实验，发射效率由1.14%提高到2.02%。

［1］GERARD Meunier，SHEN Dazhong，COULOMB Jean-Louis．Modelisation of 2D axisymmetric magnetodynamic domain by the finite element method［J］．IEEE Transactions on Magnetics，1988，24(1):166－169．

［2］MURAMATSU K，NAKATA T，TAKAHASHI N，et al．Comparison of coordinate systems for eddy current analysis in moving conductors［J］．IEEE Transactions on Magnetics，1992，28(2):1186－1189．

［3］LOMBARD P，MEUNIER G．A general purpose method for electric and magnetic combined problems for 2D，axisymmetric and transient systems［J］．IEEE Transactions on Magnetics，1993，29(2):1737－1740．

［4］OSAMA A．Mohammed，FUAT G．Vler．Comparison of two techniques for the solution of the 3-D nonlinear transient eddy current problem［J］．IEEE Transactions on Magnetics，1992，28(2):87－90．

［5］谢德馨，杨仕友．工程电磁场数值分析与综合［M］．北京:机械工业出版社，2008:248－249．

［6］LEONARD P J，HILL-COTTINGHAM R J，RODGER D．3D finite element models and external circuits using the Aψ scheme with cuts［J］．IEEE Transactions on Magnetics，1994，30(5):3220－3223．

［7］GARY Bedrosian．A new method for coupling finite element field solutions with external circuits and kinematics［J］．IEEE Transactions on Magnetics，1993，29(2):1664 －1668．

［8］TSUKERMAN I A，KONRAD A，MEUNIER G，et al．Coupled field-circuit problems:trends and accomplishments［J］．IEEE Transactions on Magnetics，1993，29(2):1701 －1704．

［9］王胜辉．大型变压器场路耦合瞬态涡流场及螺旋线圈轴向电流效应研究［D］．沈阳:沈阳工业大学，1999．

［10］王晓远，李娟，丁亚明，等．永磁体内涡流场对同步电机电枢电流的影响［J］．微特电机，2007，35(12):9 －11．

WANG Xiaoyuan，LI Juan，DING Yaming，et al．Influence of eddy current field in the permanent magnet on the armature current of synchronous machines［J］．Small-Special Electric Machines，2007，35(12):9 －11．

［11］邹本贵，曹延杰，王成学，等．单级同步感应线圈炮电枢的磁场－温度场有限元分析［J］．电机与控制学报，2011，15(2):42－47．

ZOU Bengui，CAO Yanjie，WANG Chengxue，et al．Finite element analysis of magnetic-thermal fields for armature in singlestage synchronous induction coilgun［J］．Electric Machines and Control，2011，15(2):42 －47．

［12］张洋，白保东，谢德馨．三维瞬态涡流－电路－运动系统耦合问题的新解法［J］．中国电机工程学报，2008，28(9):139－144．

ZHANG Yang，BAI Baodong，XIE Dexin．New method to solve 3D transient electromagnetic field-circuit-motion coupling problem［J］．Proceedings of the CSEE，2008，28(9):139 －144．

［13］阎秀恪．开关磁阻电机性能的场－路－运动耦合分析［D］．沈阳:沈阳工业大学，2004．

［14］梁振光，唐任远．大型变压器三维瞬态涡流场场路耦合模型［J］．电工技术学报，2003，18(5):20 －21．

LIANG Zhenguang，TANG Renyuan．Coupled field － circuit model of 3D transient eddy current field for large transformers［J］．Transactions of China Electrotechnical Society，2003，18(5):20－21．

［15］颜威利，杨庆新，汪友华，等．电气工程电磁场数值分析［M］．北京:机械工业出版社，2005:249－250．

［16］谢处方，饶克谨．电磁场与电磁波［M］．北京:高等教育出版社，2006:63－64．

［17］博弈创作室．APDL参数化有限元分析技术及其应用实例［M］．北京:中国水利水电出版社，2004:1－2．

［18］RONALD J Kaye，GREGORY A Mann．Reliability data to improve high magnetic field coil design for high velocity coilguns［R］．Albuquerque，New Mexico:Sandia National Laboratories，2003．

［19］BARRY Marder．SLINGSHOT-a coilgun design code［R］．Albuquerque，New Mexico:Sandia National Laboratories，2001．