用于旋转调制捷联惯导系统的旋转控制方法

刘芳， 王玮， 张仲毅

(北京航空航天大学仪器科学与光电工程学院，北京 100191)

0 引言

20世纪70年代至今，旋转调制式捷联惯导技术得到诸多应用和发展。国外方面包括Delco公司的代表产品“轮盘木马”400［1］(C －400)，Litton 公司研制的低成本高精度的激光捷联惯导系统LN－94［2］，以及英国 MARLIN 开发项目下的 MK49［3］;国内方面包括北京理工大学对旋转调制式光纤陀螺捷联惯导系统的误差特性进行的仿真研究［4］，以及国防科技大学研制的用于长航时的高精度激光陀螺单轴旋转惯性导航系统［5］。可以说旋转调制式捷联惯导技术受到越来越多的重视，该技术利用原有的惯性器件却可以大幅度提高系统的导航精度［6］。与旋转调制式捷联惯导技术相匹配的旋转控制技术目前已发展出了连续单方向旋转、连续正反转和转位置这三种方式，其中的连续正反转从旋转调制的效果上讲较另外两种方式更具有优势，主要体现在刻度系数误差不积累，避免使用滑环，可靠性好，但控制难度也最大，对于某些高精度系统要求反转瞬间角度误差很小。

目前已发展出许多种电机控制策略，包括PID(proportional－integral－differential)控制、模糊控制和神经网络［7～10］等，往往采用闭环控制。PID控制是工程上最常用的一种控制方法，其结构简单并易于实现，但一般难以满足某些高精度系统的性能要求，而其它的现代控制方法虽然从理论上讲在某种程度上能够提高控制性能，但在工程实际应用中却增加了系统的复杂性而降低了可靠性。常见的电机正反转控制主要是针对速度控制，而反转瞬间角度的控制精度不高，大多数是从硬件上解决的［11－12］，需要设计特殊的电路结构;也有采用现代控制策略的［13－14］，而对于旋转调制式捷联惯导系统，电机转速一般在几度每秒至几十度每秒之间，这些控制策略在中低转速的控制系统中相比于常规PID控制并不能体现出明显优势，运算量也相对较大，在实时运算中往往需要相应的硬件设计［15］。

针对上述背景，给出了一种相比于其它的控制算法更为简单易行的，应用于高精度旋转调制捷联惯导系统的直流电机正反转控制方法，只需具有位置反馈的单闭环控制回路，采用PID控制与开环控制相结合的控制技术和系统调试方法，在仿真的基础上对某型采用挠性器件的双轴旋转调制式捷联惯导系统进行了实际调试，调试结果达到了系统精度要求。

1 系统介绍

双轴旋转调制式捷联惯导系统由两个独立的单元体构成，系统实物图如图1所示。坐标系定义如图2所示，单元体1旋转轴与机体轴Z方向一致，单元体2旋转轴与机体轴Y负方向一致。每个单元体内有两个挠性陀螺和两个挠性加计，对应敏感轴的x、y方向。开机后电机首先寻零，然后两个单元体同时正反转，将敏感轴的角速度和加速度分解到机体轴上，其中单元体1经旋转分解后得到X、Y轴导航数据，单元体2经旋转分解后得到Z轴导航数据。单元体1调制水平方向的陀螺漂移，单元体2调制垂直方向的陀螺漂移。这种系统结构仍然使用原有的惯性器件并且不改变已经成熟的导航算法，采用机械旋转的方式达到减小陀螺漂移的目的，基本上可以使系统的导航精度提高一个量级。

图1 旋转调制捷联惯导系统实物图Fig．1 The rotation-modulation strap-down inertial navigation system

图2 系统结构示意图Fig．2 Structure of RM SINS

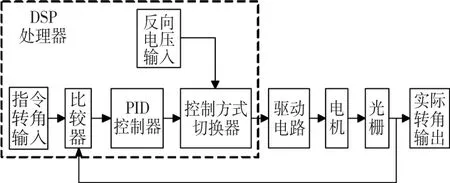
图3 旋转控制系统框图Fig．3 Flow of rotation control

为了最大程度减小系统复杂程度，电机旋转控制系统采用具有位置反馈的单闭环结构，如图3所示。系统采用国产J80LYX01F1型永磁直流力矩电机，参数为:转动惯量约为0.001 kg·m3(包含负载)，电枢电阻为3.5 Ω，电枢电感为2.6 mH，力矩系数为0.08 N·m/A，静摩擦力矩为0.045 N·m。DSP的型号为TMS320F2812，采用英国Renishaw的光栅，其分辨率为1.44″，刻线精度 ±3.6″。电机的旋转控制算法在DSP芯片内完成，其输出经驱动电路放大后给到电机，再通过光栅读出转角反馈给DSP。

2 旋转控制误差对导航的影响

在理想情况下，敏感轴陀螺漂移经过旋转分解后被调制成正弦或者余弦振荡，如式(1)所示，其中Δεx1、Δεy1表示单元体1 的敏感轴漂移，ΔεX、ΔεY表示单元体1的机体轴漂移。

在实际情况下，旋转控制误差会导致机体轴上存在不可调制漂移，表现出的形式为:在电机平稳旋转阶段，旋转控制误差类似于噪声，这会增大机体轴角速度上的随机游走;在电机反转期间，旋转控制的超调误差使得敏感轴漂移在这段时间内不能被完全调制，经过长时间累计后可造成导航误差。

目前，从工程经验的角度提出的控制要求是:平稳旋转时的角度误差小于10″，反转时的最大角度误差小于30″。该误差对于导航的影响可以忽略不计。

3 旋转控制算法流程

控制算法流程图如图4所示。第n时刻的指令转角为

其中:ωl为理想转速;Δt为采样周期。

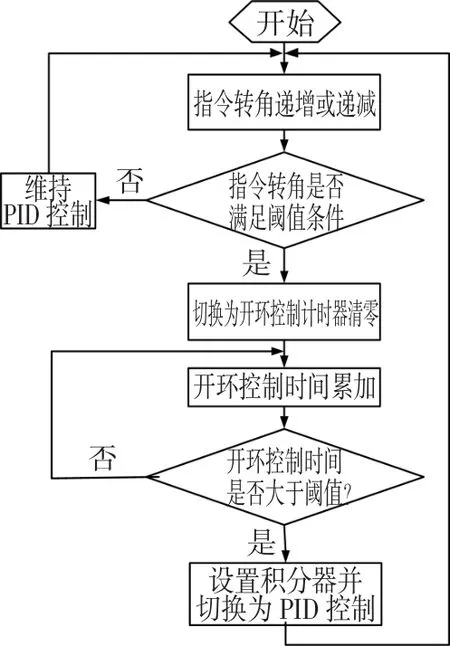
图4 算法流程图Fig．4 Computation scheme of rotation control

为了保证平稳旋转时的精度并具有足够的抗干扰性，在电机匀速旋转时采用PID控制方式。当指令转角θin在正转过程中满足θin＞θ1或在反转过程中满足 θin＜ θ2(其中 θ1略小于360°，θ2略大于0°)，即认为电机开始反转，控制方式切换为开环控制方式，否则继续维持PID控制方式。在开环控制方式中，在电机两端施加几伏到二十几伏的电压，并且当开环控制计时器的累计时间大于阈值(一般为1～10 ms)时再切换回PID控制，并设置积分器的初值，电机又开始匀速转动。

4 系统调试方法

4.1 系统模型

系统模型框图如图5所示，其中:P、I、D分别为比例、微分和积分控制器参数;U为控制电机的电压;ω为电机的角速度;L为电枢电感;R为电枢电阻;I为电机的电流;Cm为力矩系数;M为输入给电机的控制力矩;J为电机的转动惯量;B为粘滞摩擦系数;Mf库伦摩擦力矩;Ce为反电势系数。系统模型中包括控制器模型、电机模型和光栅模型。其中控制器模型包括PID控制器和控制方式切换器，电机模型［16］的表达式为

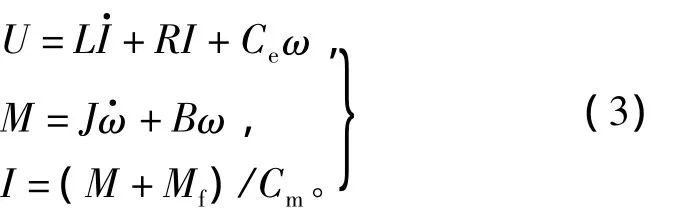
其中光栅模型即为积分器。

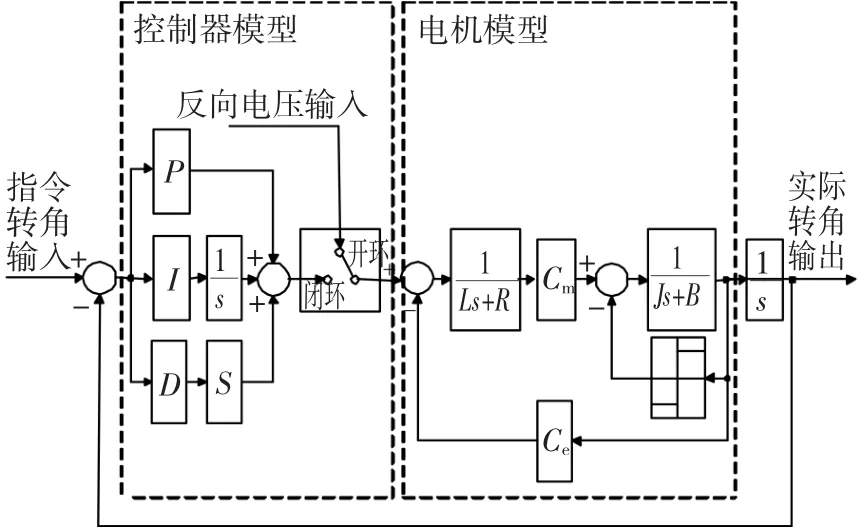
图5 系统模型框图Fig．5 The system rotation control model

实际系统的转动惯量J和粘滞摩擦系数B一般很难估计，可以把系统近似为一阶模型并进行参数辨识［17］。

4.2 PID参数的整定

PID参数的整定采用Z－N整定法，PID控制器的输出为

其中:e为角度误差;Kp为比例增益;Ti为积分时间常数;Td为微分时间常数;这里令P=Kp，I=Kp/Ti，D=KpTd。系统闭环，令I=0，D=0，给电机输入一单位阶跃电压，逐渐增大P，直至电机转角出现等幅振荡，记下此时的比例增益Pu和振荡周期Tu，则Ti=0.5Tu，Td=0.125Tu，P=0.6Pu。该参数整定方法只用在仿真中，实际中参照仿真的结果。

4.3 反转瞬间的开环控制

电机反转前转换为开环控制，对电机施加1～10 ms的反向电压，其大小记为UT。由图4可知，若不考虑摩擦和反电动势，忽略电枢电感，则输入电压U和控制力矩M之间的关系近似为

在仿真和实际中再微调UT直至控制方式由开环控制切换到PID控制的时刻电机转速尽量接近反转后平稳旋转时的速度。

4.4 反转后PID控制器的设置

PID控制器中的积分器具有记忆功能，在电机平稳旋转时，积分器的输出用于抵消阻力。所以在电机反转后要根据阻力情况设置积分器中的值，使之快速过渡到平稳旋转时的稳态值。

由图4可知电机平稳旋转时的阻力由静摩擦力矩、粘滞摩擦力矩和反电动势等效力矩三部分构成，其中后两项与电机的转速成正比，所以积分器稳态值的计算公式为

在电机即将反转时加反向力矩MT，所加时间为ΔT，电机平稳旋转时的转速大小为ωc，根据刚体转动动力学原理，则有

由式(5)和式(6)可得到反向电压UT的近似计算公式为

在仿真或实际中，可以根据式(8)设置控制方式转换后的积分器初值，若摩擦力矩和反电势系数很小，也可直接将积分器清零。

5 系统仿真结果

针对国产J80LYX01F1型永磁直流力矩电机进行了SIMULINK仿真，开环控制时间为1 ms，电机平稳旋转时的转速为11.25°/s，由式(7)估算的反向电压的大小为17.2 V，仿真中是在电机反转前1 ms加了大小为18 V的反向电压，转为PID控制时根据式(8)将积分器初值大小设为1.97 V。

图6给出了用常规PID控制与新方法的仿真结果对比，图6(a)为角度误差的对比，图6(b)为角速度的对比。采用常规PID控制时，电机在平稳旋转时无稳态误差，反转瞬间的最大角度误差为174″，角速度超调为56.4%，调节时间约25 ms;采用新控制方法后，电机在平稳旋转时无稳态误差，反转瞬间的角度误差小于30″，角速度超调为1.5%，调节时间小于20 ms。

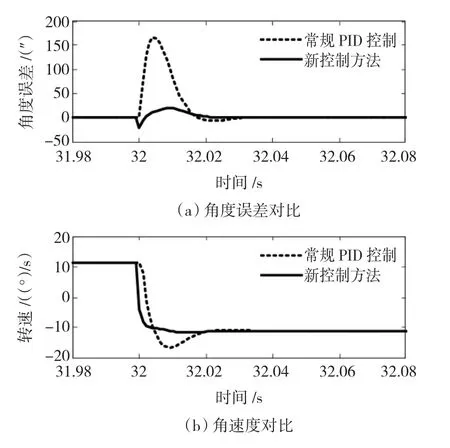
图6 常规PID控制与新方法的仿真结果对比Fig．6 Comparing simulation result of common PID with the new methods’

6 实际系统调试结果

在实际中对上述J80LYX01F1型电机进行调试，开环控制时间为1 ms，电机平稳旋转时的转速为11.25°/s，实际中是在电机反转前1 ms加了大小为18 V的反向电压，转为PID控制时积分器的设置参考仿真的结果进行了微调。电机在平稳旋转时稳态误差的标准差为2.3″。

图7给出了用常规PID控制与新方法的实际调试结果对比。采用常规PID控制时，反转瞬间的最大角度误差为180″，反转的调节时间约为40 ms，角速度超调为157.8%;采用新控制方法后，反转瞬间的角度误差小于20″，反转的调节时间小于40 ms，角速度超调为1.6%，反转过程非常平稳，满足系统精度要求。

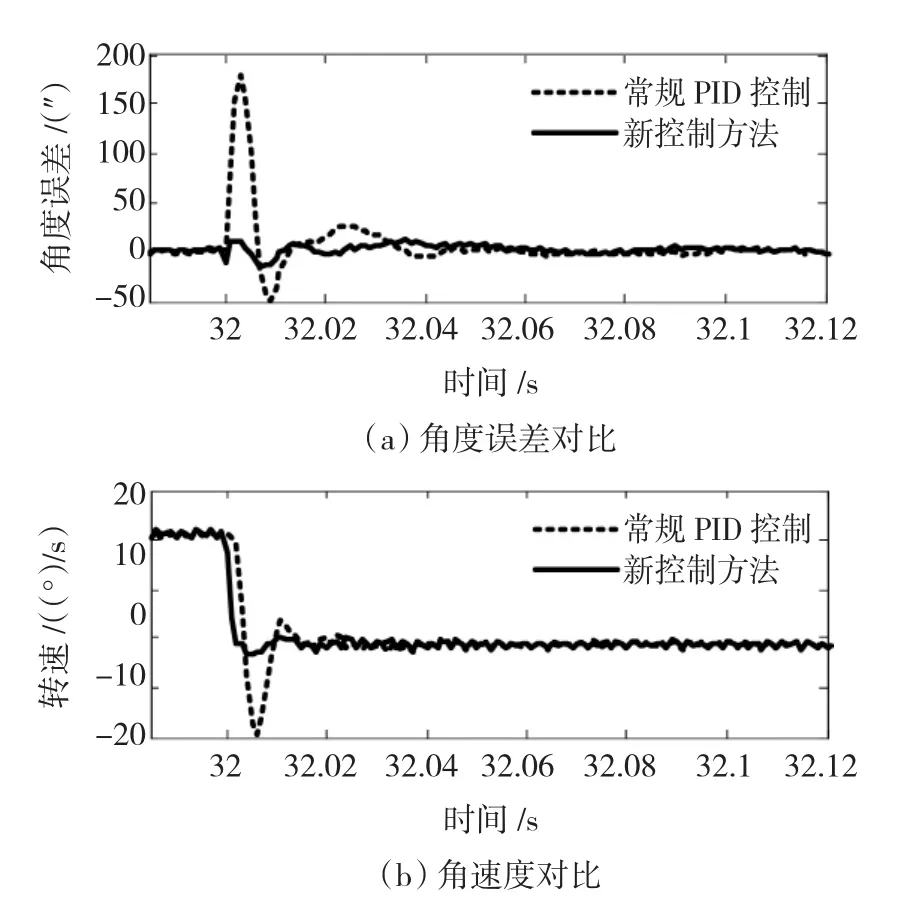
图7 用常规PID控制与新方法的实际调试结果对比Fig．7 Comparing actual result of common PID with the new methods’

7 结论

系统仿真结果和实际系统的调试结果表明，这种应用于高精度旋转调制捷联惯导系统的PID控制与开环控制相结合的直流电机正反转控制方法是有简单而有效的，这体现在:

1)使反转瞬间的角度误差降至30″以下，角速度超调小于2%，实现了电机的平稳反转。

2)与常规PID控制方法相比角位置和角速度精度均大幅度提高。

3)采用软件方法解决了如何在两种控制方式间进行切换的问题，保证了控制方式转换时的平稳过渡。

［1］陀螺仪与惯性导航专业情报网．国外惯性技术手册［M］．北京:国防工业出版社，1983:235－238．

［2］FULFROST J，CHECCO W J．Ring laser gyro navigator for surface combatant ships［J］．IEEE PLANS，1984:348 －357．

［3］LEVISON E，TER Horst J，WILLCOCKS M．The next generation marine inertial navigator is here now［C］//1994 IEEE Position location and Navigation Symposium，April 11－15，1994，Las Vegas，USA．1994:121 －127．

［4］高亚楠，陈家斌，杨亭鹏．捷联式光纤陀螺罗经系统误差分析［J］．北京理工大学学报，2005，25(5):423－426．

GAO Yanan，CHEN Jiabin，YANG Tingpeng．Error analysis of strapdown optic fiber gyro compass［J］．Journal of Beijing Institute of Technology，2005，25(5):423 －426．

［5］龙兴武，于旭东．激光陀螺单轴旋转惯性导航系统［J］．中国惯性技术学报，2010，18(2):149－153．

LONG Xingwu，YU Xudong．Single-rotating inertial navigation system with ring laser gyroscope［J］．Journal of Chinese Inertial Technology，2010，18(2):149－153．

［6］LEVINSON E，MAJURE R．Accuracy enhancement techniques applied to the marine ring laser inertial navigator(MARLIN)［J］．Journal of The Institute of Navigation，1987，34(1):64－86．

［7］YASUHIKO Dote．Application of modern control techniques to motor control［J］．Proceedings of IEEE，1988，76(4):438 －455．

［8］张凌云，赖豪杰．先进控制理论及策略在电机控制中的应用［J］．电机技术，2005，2:38－41．

ZHANG Lingyun，LAI Haojie．Application of advanced control theories and strategies in motor control［J］．Electrical Machinery Technology，2005，2:38－41．

［9］HU B G，MANN G K I，GOSINE R G．New methodology for analytical and optimal design of fuzzy-PID controllers［J］．IEEE Transactions on Fuzzy Systems，1999，7(5):521－539．

［10］ADHAVAN B，KUPPUSWAMY A，et al．Field oriented control of permanent magnet synchronous motor(PMSM)using fuzzy logic controller［J］．Recent Advances in Intelligent Computational Systems，2011，9:587 －592．

［11］周凤争，沈建新．带正反转功能的通用型无刷直流电机控制器设计［J］．2007，10:43－44．

ZHOU Fengzheng，SHEN Jianxin．Design of universal PM BLDC motor controller with reversion function［J］．Micromotors Servo Technique，2007，10:43 －44．

［12］胡海云．基于DSP的无刷直流电机控制系统研究［D］．上海:上海交通大学，2003．

［13］XIE Zengrong，LIANG Deliang．Research on control system of linear PM brushless DC motor based on single neuron PID［C］//ICEMS 2005，Sept 27－29，2005，Nanjing，China．2005:385－387．

［14］嵇艳鞠，李肃义．基于单神经元自适应PID的PLC直流电机控制系统［J］．吉林大学学报，2007，25(5):526 －532．

JI Yanju，LI Suyi．Control system of PLC DC electric motor based on single neuron self-adaptive PID controller［J］．Journal of Jilin University，2007，25(5):526－532．

［15］JEFFREY R，MOUNTAIN．Fuzzy logic motor speed control with real-time interface using an 8-bit embedded processor［C］//42nd South Eastern Symposium，March 7 －9，2010，Texas，USA．2010:307－312．

［16］GEHMLICH D K，KUO B C．直流电动机及其控制系统［M］．哈尔滨:哈尔滨工业大学出版社，1984:64－66．

［17］薛定宇．控制系统计算机辅助设计－Matlab语言与应用:2版［M］．北京:清华大学出版社，2006:263－267．