考虑电枢速度的多级感应线圈炮最佳触发位置

向红军， 李治源， 袁建生

(1．清华大学电机系，北京 100084;2．军械工程学院弹药工程系，河北石家庄 050003)

0 引言

感应线圈炮具有电枢与驱动线圈无电气和机械直接接触、可控性好、可实现较高发射初速等优点，应用前景广阔［1－7］。但是，电枢仅在驱动线圈的后半段才受到加速力，而在前半段会受到制动力，由于感应线圈炮的这一原理性弊端，使得单级驱动线圈对电枢的加速能力有限。为使电枢获得较大出口速度，可以利用多个驱动线圈，使储能电容对驱动线圈依次触发放电或供电，实现对电枢的连续加速。

多级感应线圈炮中驱动线圈的触发或导通时机是影响电磁发射效率的重要因素。对于多级感应线圈炮中的任一级驱动线圈，如果触发放电时间过早，该驱动线圈就会对电枢提供制动力;如果触发过晚，对电枢的有效加速时间会缩短，从而影响其加速性能。显然，电枢和驱动线圈之间存在一个最佳触发位置，即当电枢处于驱动线圈的一个合适位置时触发，电枢会获得最大的加速效果。

已有许多文献研究过最佳触发位置问题［8－11］，但大都没有充分考虑最佳触发位置与电枢速度的关系。本文从电枢受到的电磁力计算公式出发，系统分析了各参数对电枢加速作用的影响，并首次给出了考虑电枢速度下最佳触发位置变化特性及其产生原因，对解决多级感应线圈发射过程中的触发控制难题提供了理论基础。

1 最佳触发位置分析

感应线圈炮的结构原理如图1(a)所示。主要由储能电容器C、触发开关、驱动线圈、续流二极管D和电枢构成。如果不考虑电枢的趋肤效应，可以将电枢等效为单匝线圈，因此可得到感应线圈炮的等效电路模型如图 1(b)所示，Ld、Lp、Rd、Rp分别为驱动线圈和电枢回路的等效电感和等效电阻，M为两者之间的互感。

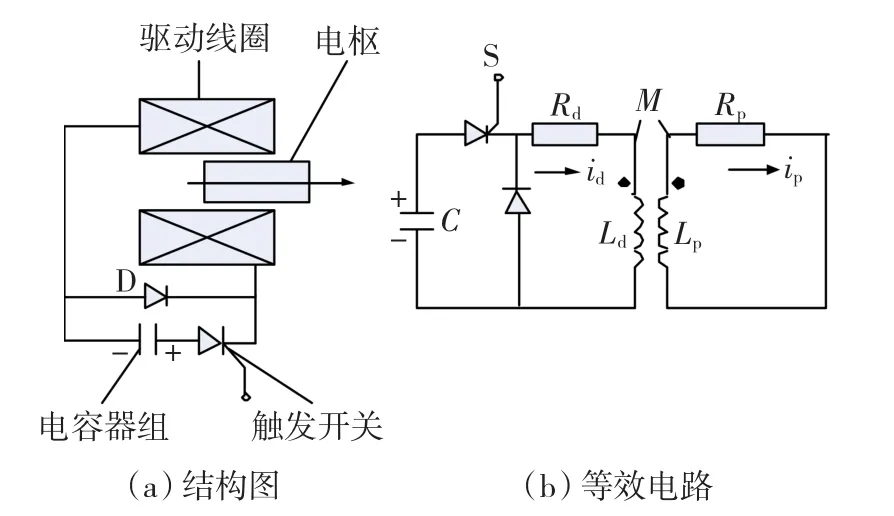
图1 感应线圈炮工作原理Fig．1 Principle of the inductive coilgun

电容器组向驱动线圈放电产生脉冲磁场，从而在电枢中感应出电流，电流在磁场作用下，会使电枢受到电磁力作用。

电枢在驱动线圈中受到的电磁力可表示为［12－15］

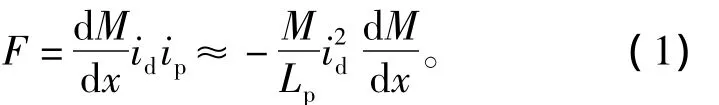
式中:id为驱动线圈的电流;ip为电枢中感应的电流;dM/dx为互感对电枢位置的梯度。

从式(1)可以看出，电枢所受的电磁力正比于电枢与驱动线圈间的互感、互感梯度、驱动线圈中的电流。下面分析影响电枢加速效果的因素。

1.1 影响加速效果的因素分析

当驱动线圈和电枢的中心面重合时，互感M最大，但互感梯度dM/dx为零，由式(1)可知，电枢所受电磁力为零;当电枢移出驱动线圈，且远离线圈时，则互感趋于零。电枢处于驱动线圈的不同位置时，互感和互感梯度相差很大，随着电枢从驱动线圈的中心向线圈外移动，互感与互感梯度的乘积MdM/dx呈现一个脉冲形式变化，如图2所示。图中横坐标s为电枢中心面距驱动线圈中心面的距离，纵坐标为MdM/dx。因此，从互感与互感梯度角度看，电枢所受的电磁力随s或时间成脉冲形式变化。

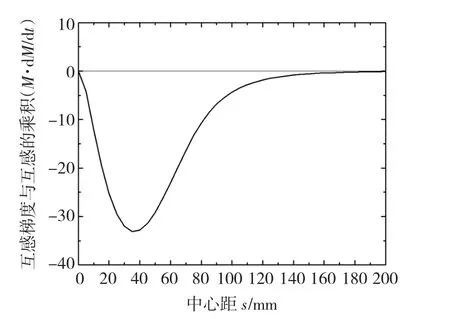
图2(MdM/dx)随电枢位置的变化示例Fig．2 Variation instance of M·dM/dx according to the location of armature

采用储能电容器作为电源的感应线圈炮，由于线圈的电感作用，使得激励电流id不可能跃变，从零到达最大值需要一定时间，形成电流脉冲的前沿，如图3所示。图中给出了电枢初始速度为不同值时的驱动线圈放电电流波形，其对应的电路参数将在后面给出。因此，从驱动线圈的激励电流id角度看，电枢所受的电磁力随时间也成脉冲形式变化。

图3 驱动线圈中的电流示例Fig．3 Instance of current in driving coil

由于影响电磁力的两个因素MdM/dx和id都为脉冲形式，由式(1)可以得出，电磁力也应为脉冲形式。其示例曲线如图4所示。从图4可以看出，驱动线圈在t1时刻开始放电，此时电枢的中心面位于驱动线圈中心面的左侧，互感梯度为正，由式(1)可知电磁力首先为负;到达t3时刻时，两者中心面重合，电磁力为0;此后电枢的中心面位于驱动线圈中心面右侧，互感梯度为负，则电磁力为正;达到t4时刻后，由于电枢感应电流方向发生改变，电磁力再次发生反向为负;t2时刻电枢离开驱动线圈，电磁力作用结束。图4中电磁力为正的区间称为有效加速区间，即t3到t4之间的区间。

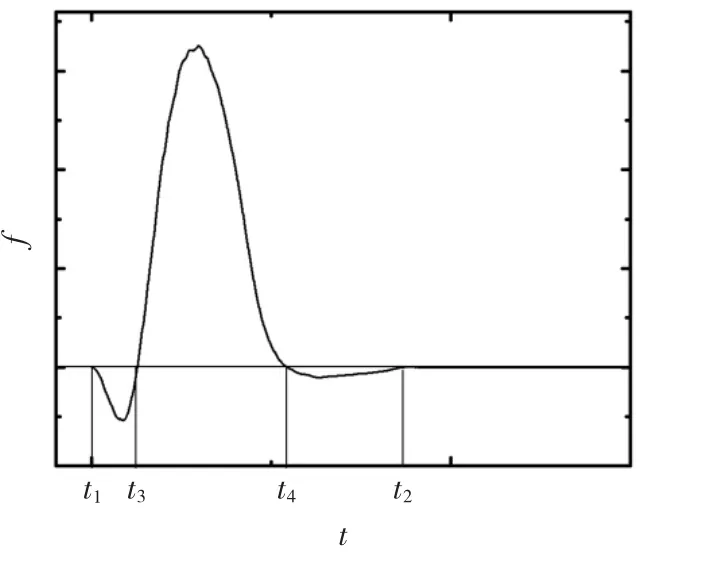
图4 电磁力示例曲线Fig．4 Instance curve of electromagnetic force

由冲量定理可知，电枢在驱动线圈中获得的速度增量与电磁力及其作用时间密切相关，速度增量与加速力的关系为

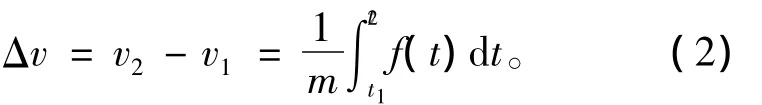
式中:v1和v2分别为电枢进入驱动线圈时的速度(称为注入速度)和离开驱动线圈时的速度(称为出口速度);m为电枢质量;f为电枢受到的加速力。

从式(2)可知，要使电枢获得较大的速度增量，就要使在t3到t4时间段内不仅电枢所受的电磁力要比较大，而且Δt=t4－t3要相对较长。但实际上电枢速度越快，则Δt会越小。

因此，要确定合适的触发位置，获得良好的加速效果，不仅要充分考虑触发时间的问题，同时要考虑电磁力的大小。

1.2 最佳触发位置确定方法

由于驱动线圈中的电流脉冲波形和电感梯度脉冲波形都有一个逐步上升的过程，刚开始的时候，两个脉冲MdM/dx和id的值都比较小，因而电磁力的数值也比较小。从式(2)可知，在电枢经过驱动线圈所需要的时间一定的情况下，如果有效加速区间Δt对应的正向电磁力数值比较小，则电枢的速度增量也比较小，加速效果不明显。

如果两个脉冲上升到一定数值时，两者乘积较大且正向电磁力数值比较大，如果电磁力数值比较大的区间正好位于有效加速区间之内，则从式(2)可知，电枢的速度增量会比较大。

因此，触发位置的确立要同时考虑电枢位置、电枢当前已具有的速度和驱动线圈电流的上升时间。在有限加速区间内，要充分利用两个脉冲数值较大的区间。

在驱动线圈各级参数相同的情况下，尽管电枢速度不断提高，但驱动线圈的放电电流曲线变化非常微小，从图3也可以看出。但由于电枢运动经过驱动线圈的时间缩短，要想充分利用两个脉冲乘积较大即电磁力较大的区间，使其位于有效加速区间之内，就要随着电枢速度增加，触发位置不断提前，当电枢速度较高时，最佳触发位置甚至会提前到电枢处于制动力的位置。因为最佳触发位置不是考虑触发时刻一点的效果，而是要考虑整个时间段内的整体加速效果。采用这样的策略，看上去电枢在一定区间会受到制动力，但却可以使电枢受到的总速度增量达到最大。

确定一定线圈结构和电容供电系统下，不同电枢速度对应的最佳触发位置，可以通过数值计算软件计算出不同速度和不同电枢位置下的加速效果，从而可以得到每个速度下加速效率最大的电枢位置，该位置便是最佳触发位置。下面通过仿真计算结果具体论述最佳触发位置及其确定方法。

2 最佳触发位置有限元仿真结果与分析

最佳触发位置与电枢固有的速度有关，即进入本驱动线圈时的速度，或称为注入速度。下面利用有限元软件Ansoft瞬态场与电路耦合对不同注入速度的电枢进行了仿真，以分析最佳触发位置对应的中心距s的变化规律。定义驱动线圈中心面到电枢中心面之间的距离为中心距s，并规定沿电枢运动方向为正方向。

2.1 仿真模型建立

由于驱动线圈和电枢都是轴对称结构，因此选择轴对称模型建立的计算模型剖分后如图5所示。模型结构参数为:驱动线圈轴向长度80 mm;径向厚度20 mm;电枢的轴向长度为60 mm;径向厚度为20 mm;电枢的材料选择为铝，驱动线圈的材料选择为铜。外边界条件设为长300 mm、高1 300 mm，并设为气球balloon边界，电枢和发射载荷总质量为3 kg，驱动线圈匝数设为30匝。

仿真中的激励源由外挂激励电路提供，实际线圈炮电路中，为防止电容反向充电而降低使用寿命，通常在电容两端并联续流二极管。因此设计的外挂电路如图6所示。电容值C为2 000 μF，初始电压设为10 000 V，驱动线圈回路总电阻100 mΩ。

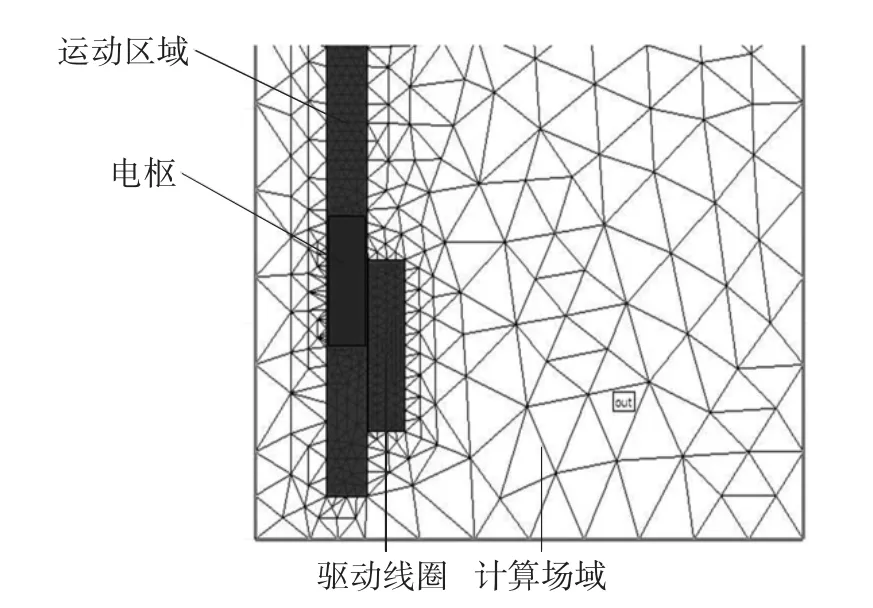
图5 计算模型Fig．5 Simulation model

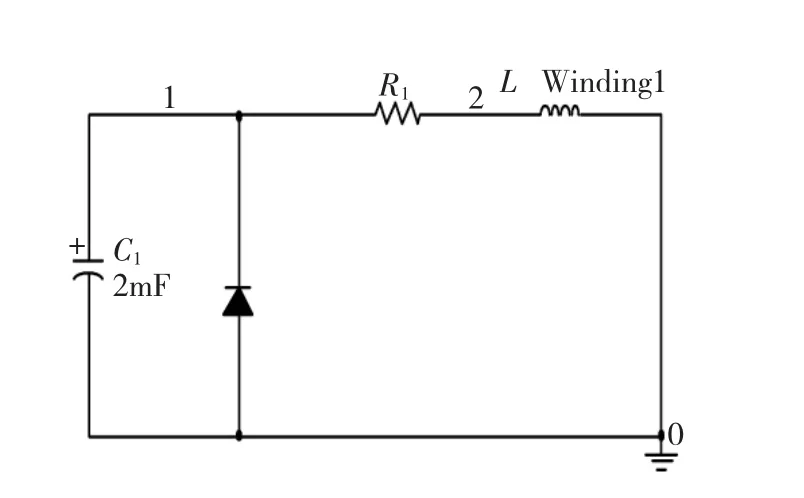
图6 激励电路Fig．6 Driving circuit

2.2 仿真结果及分析

对图5所示的模型在电枢注入速度为0、50、100、150、200、250 m/s时，分别进行了仿真计算，得到的触发位置(中心距)s与电枢入口速度之间的关系如表1所示(部分结果)。

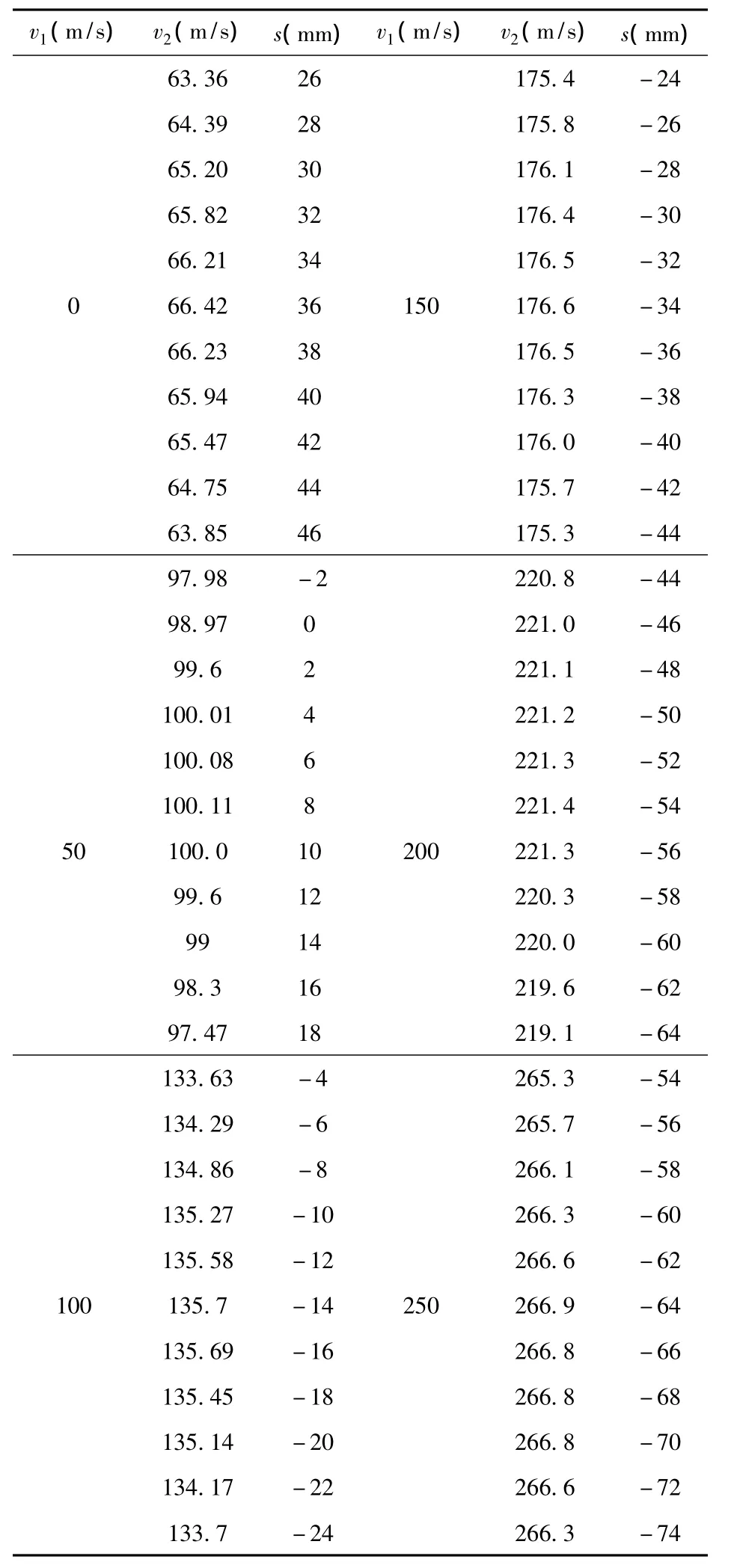
表1 触发位置仿真数据表Table 1 Simulation data of trigger position

从表1可以看出，当电枢初速为0、50、100、150、200、250 m/s时，最佳触发位置 s分别为 36、8、－14、－54、－64，电枢最佳触发位置与电枢注入速度之间的关系曲线如图7所示。

从图7可以看出，在驱动线圈各级参数相同的情况下，随着电枢速度的提高，最佳触发点的位置逐渐提前，甚至出现驱动线圈到电枢之间的中心距为负值的情况，这表明最佳触发位置使得电枢的中心面位于驱动线圈中心面的后面，即高速运动的电枢先经过一段时间制动、再加速，反而会获得更高发射效率，仿真结果映证了理论分析得出的结论。

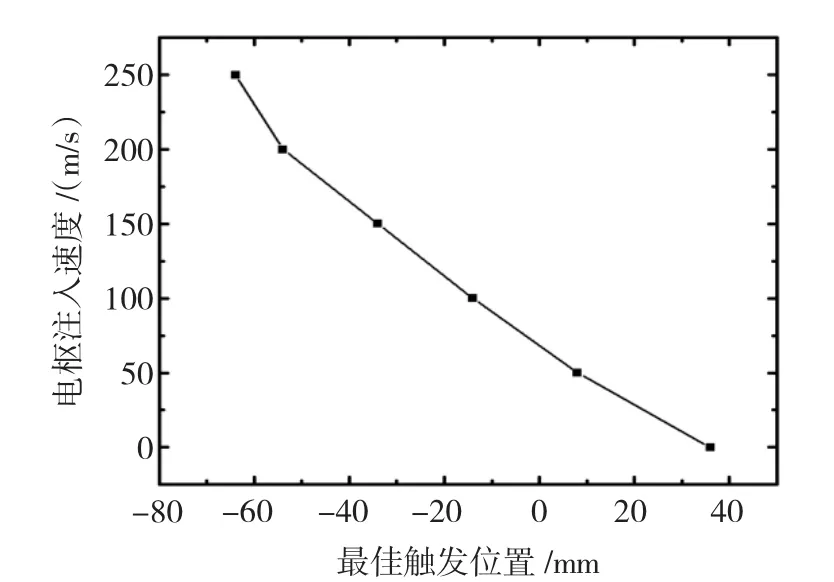
图7 电枢注入速度与最佳触发位置的关系Fig．7 Relative curve of initial velocity and optimal trigger position

3 触发控制策略

通过理论和仿真分析可知，对于一个确定的多级线圈发射装置，不同的电枢入口速度对应驱动线圈的不同最佳触发位置，因此可以利用驱动线圈的最佳触发位置与入口速度之间的对应关系来实现多级感应线圈炮的同步触发。

从图7可以看出，电枢的注入速度v1和最佳触发位置s之间存在一定函数关系，可以表示为

对于不同的发射系统或不同结构驱动线圈，具有不同的函数关系g。通过对图7所示的数值关系进行曲线拟合可以得到g函数关系式。理论上，只要数据量足够，可以得到比较准确的函数关系g。

因此可以采用硬件测速加软件延时相结合的方法来实现同步触发。其具体思路为:在每相邻两级驱动线圈之间安装速度传感器，实时测得电枢进入驱动线圈的速度，触发系统中的微处理器如单片机利用f函数就可以计算得到下一级驱动线圈的触发位置s，并将触发位置s转换为下一级驱动线圈放电开关的延迟触发时间，利用单片机延时触发，延时完毕，开关闭合，实现驱动线圈在最佳触发时刻触发放电，达到同步触发。

4 结论

多级同步感应线圈炮的每一级驱动线圈都存在一个最佳触发位置，而且随着电枢注入速度的增加，最佳触发位置不断提前。因此，对于某个特定的发射系统，可以通过仿真或试验得到电枢的入口速度与最佳触发位置之间的对应关系，然后利用硬件测速与软件延时相结合的方法，测得电枢速度，并将驱动线圈的最佳触发位置转化为驱动线圈的放电延时时间，可以消除延迟时间和电枢速度的累积误差，实现同步触发。

［1］BENJAMIN D S，RANDY L G．Multimission electromagnetic launcher［J］．IEEE Transactions on Magnetics，2009，45(1):458－461．

［2］WILLEM J K，FRANCIS J．Electric energy gun technology:status of the French-German-Netherlands program ［J］．IEEE Transactions on Magnetics，1999，35(1):25－30．

［3］JAMET F，WEGNER V，PETER H．Some aspects of future military requirements［J］．IEEE Transactions on Magnetics，1993，29(1):351－353．

［4］VOLODYMYR T C．Review of the recent works of ukrainian authors in the field of electromagnetic acceleration and related topics［J］．IEEE Transactions on Magnetics，2001，37(1):21 －24．

［5］HE J，LEVI E，ZABAR Z，et al．Analysis of induction-type coilgun performance based on cylindrical current sheet model［J］．IEEE Transactions on Magnetics，1991，27(1):579 －584．

［6］RICHARD R B．Electromagnetic aircraft launch system development considerations［J］．IEEE Transactions on Magnetics，2001，37(1):52－54．

［7］FAIR H D．Advances in electromagnetic launch science and technology and its applications［J］．IEEE Transactions on Magnetics，2009，45(1):225－230．

［8］曹延杰，刘文彪，张媛，等．单级感应线圈炮最佳触发位置仿真研究［J］．计算机仿真，2006，23(12):9 －11．

CAO Yanjie，LIU Wenbiao，ZHANG Yuan，et al．Simulation and analysis of single stage induction coilgun’s best initial position［J］．Computer Simulation，2006，23(12):9－11．

［9］冯霈，雷彬，李治源．电容器参数对最佳发射初始位置影响的研究［J］．国外电子元器件，2007，(3):4－8．

FENG Pei，LEI Bin，LI Zhiyuan．Effect of launch initial position on the performance of coil gun［J］．Foreign Electronic Device，2007，(3):4－8．

［10］苏子舟，国伟，张涛，等．弹丸配重对线圈炮最佳初始位置影响研究［J］．电气技术，2010(增刊1):27－30．

SU Zizhou，GUO Wei，ZHANG Tao，et al．Effect of launch initial position on the performance of coil-gun by the pull-back weight of the projectile［J］．Electric Technology，2010(S1):27 －30．

［11］CAO Y J，LIU W B，LI R F，et al．Study of discharge position in multi-Stage synchronous inductive coilgun［J］．IEEE Transactions on Magnetics，2009，45(1):518 －521．

［12］王莹，肖锋．电炮原理［M］．北京:国防工业出版社，1995:93－106．

［13］BARRY M．A coilgun design primer［J］．IEEE Transactions on Magnetics，1993，29(1):701 －705．

［14］HE J，LEVI E，ZABAR Z，et al．Concerning the design of capacitively driven induction coil guns［J］．IEEE Transactions on Magnetics，1989，17(3):429 －438．

［15］KIM S W，JUNG H K，HAHN S Y．An optimal design of capacitor-driven coilgun［J］．IEEE Transactions on Magnetics，1994，30(2):207－211．