轧机液压伺服位置系统的自适应输出反馈控制

李建雄， 方一鸣，2， 石胜利

(1.燕山大学工业计算机控制工程河北省重点实验室，河北秦皇岛 066004;2.国家冷轧板带装备及工艺工程技术研究中心，河北秦皇岛 066004)

0 引言

电液伺服系统因其具有功率体积比大、响应速度快、控制精度高等优点，在工业过程中得到了广泛应用。但由于电液伺服系统本身具有较强的非线性特性，并存在内部参数和外负载等不确定性，这些因素增加了控制系统设计的难度。

为提高液压伺服系统的控制性能，文献［1］考虑到液压系统中存在的非线性、参数不确定性和未知外部扰动，基于非连续投影算法，提出了一种自适应鲁棒控制方法。文献［2-3］考虑到系统中存在的非线性不确定参数，通过构造一个特殊的Lyapunov函数，将非线性不确定参数问题转化为线性不确定参数问题，然后利用滑模自适应方法设计控制器，能使系统达到渐近跟踪。另外，文献［4］采用了自适应滑模变结构的方法，文献［5］将模糊神经网络的方法应用到液压伺服位置控制中。上述结果都是在假定系统所有状态可测的前提下得到的，然而，通常情况下，在液压伺服系统中并非所有状态都是可测的，如柱塞速度。

考虑到液压伺服系统中存在不可测状态，文献［6］设计了动态输出反馈控制器，文献［7］在假定只有压力可测的前提下，构造了一个PI观测器重构系统状态。考虑到不确定参数和未知外部扰动的存在，文献［8］提出了基于鲁棒自适应观测器的速度跟踪控制方法。然而，在文献［8］中，除外部扰动外，只考虑了两个参数是未知的情况，将系统转换成一个较为特殊的结构，并将一些含有输入的非线性项归为不确定项，这样处理将会在一定程度上影响控制效果。

本文在只有缸位移信号和油压信号可测的前提下，针对存在未知参数和未知外负载力的轧机液压伺服位置控制系统，提出了一种基于高增益观测器的自适应输出反馈控制算法。

对于存在未知参数的非线性系统的输出反馈控制，通常的方法是先构造带有参数估计的自适应观测器，然后基于所构造的观测器设计输出反馈控制器。常用的带有参数估计的自适应观测器有两种:一是需要满足观测器匹配条件的自适应观测器，这里的观测器匹配条件是指未知参数包含在可测输出状态的动态内，比如文献［9］的BTP=MC和文献［10］的 ψT(t)ΛST=E(t)G(t)C0。二是需要引入辅助变量的自适应观测器，比如文献［11］需要引入一个n×q维辅助矩阵变量，文献［12-13］需要引入两个分别为n×q和q×q维的辅助变量，其中n和q分别为系统状态和未知参数的维数。对于本文所考虑的液压伺服位置系统，其系统结构并不满足第一种观测器要求的匹配条件。并且由于需要估计的未知参数较多，因此，采用第二种观测器将会大大增加观测器的维数。

不同与以上的自适应观测器，本文设计的高增益观测器不依赖于系统输入和参数的估计值，只以系统的输出作为观测器输入，其结构相对简单，易于实现。除包含高增益观测器外，所设计的自适应输出反馈控制器还包括参数估计器和动态反馈控制器。理论分析表明，所提出的算法能够保证闭环系统最终有界稳定，系统状态及其估计误差最终收敛到原点的一个由高增益决定的邻域内。最后，将所设计的控制器应用到某650 mm可逆冷带轧机液压伺服位置系统进行仿真研究，仿真结果验证了所提出算法的有效性。

1 问题描述

轧机液压压下系统的执行机构采用非对称液压缸(油缸)，而非对称油缸的力平衡方程可表示为［7］

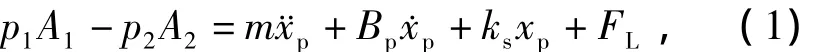
式中，p1和p2分别为油缸无杆腔和有杆腔的压力;A1和A2分别为无杆腔和有杆腔活塞的有效作用面积;xp为缸位移(其增/减对应于轧机辊缝的减/增);m为柱塞和上辊系运动部件的等效总重量;Bp为柱塞及负载运动中的粘滞摩擦系数;ks为负载弹性刚性系数;FL为作用在柱塞上的外负载力。忽略外泄漏的影响，系统的流量方程为［3，14］

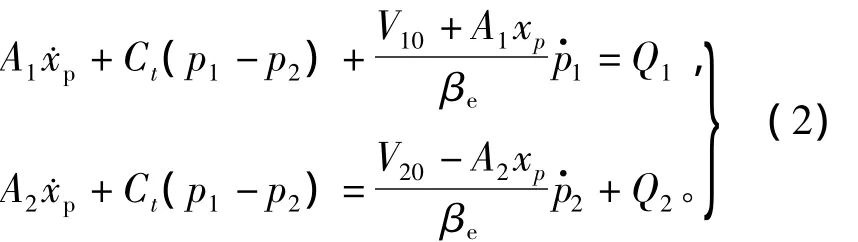
式中:Ct为液压缸内泄漏系数;βe为体积弹性模量;V10和V20分别为无杆腔及相连管道与有杆腔相连管道的初始容积;Q1和Q2分别为无杆腔流入与有杆腔流出的流量，可表示为［7，14］

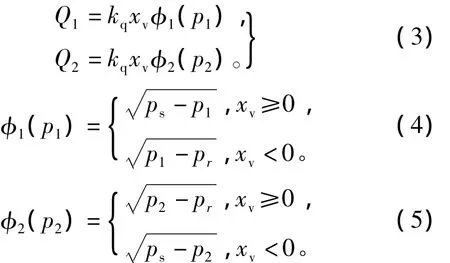
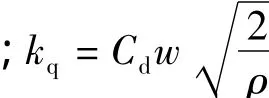
伺服阀的阀芯位移xv和伺服阀输入u之间可以近似为比例关系，即可以表示为xv=kvu，其中kv＞0为增益系数。

然后，令z1=xp，z2==xp，z=［z1z2z3］T，则由式(1)～式(5)，整理可得

首先，在液压系统中，缸位移信号y=z1=xp以及两腔压力信号p1和p2可以通过位移传感器和压力传感器测量得到。在系统(6)中，状态z2和z3的物理意义分别油缸柱塞的速度信号和加速度信号，这两个信号通常是不能直接测量的。

其次，由于油缸的冲程是有限的，即z1是有限的，进一步可以得出系统状态z是有界的，不失一般性地假设|zi|≤其中 ¯zi＞ 0=1，2，3。并考虑到油压p1和p2的有界性，可以得出，φ1(z1)，φ2(z1，p)和 φ2(z1，p)都是有界的，且 ψ(z1，p)＞0。

另外，由于参数Ct，βe，Cd，w，ρ在不同系统温度、不同工作环境等情况下是不确定的;由于管路等原因，V10和V20也不能准确测量;m不能精确已知，外负载力FL也是未知的，因此系统(6)中的参数θ，θ5和d(t)是未知的。假定 θ，θ5和d(t)都是有界的，即有 θi≤θi≤，|d|≤，其中 θi＞0＞0，i=1，…，5＞0 为已知常数。并假定未知参数 θi，i=1，…，5是定常或慢时变的。

本文的主要目的是:针对具有不可测状态、未知参数、非线性和未知干扰的系统(6)，设计控制器u使系统输出y能够快速有效地跟踪参考轨迹yr。

2 自适应输出反馈控制器设计

本节将给出一种基于高增益观测器和参数估计器的自适应输出反馈控制算法。

首先，假定参考轨迹yr有界，并且和存在且有界。令zr=［yryryr］T，e=z-zr，e=［e1e2e3］T，由式(6)，可得出误差模型为

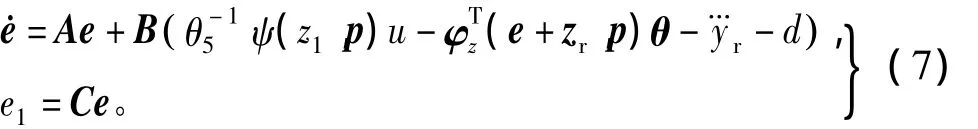
为简化和方便表示，可将函数φz(e+zr，p)表示为 φz(ζ，e2，e3)，其中 ζ=［e1，pT］T为可测量信号，e2和e3为不可测量信号。

然后，构造自适应输出反馈控制器，即

式(9)中的投影算子proj可表达为［15］

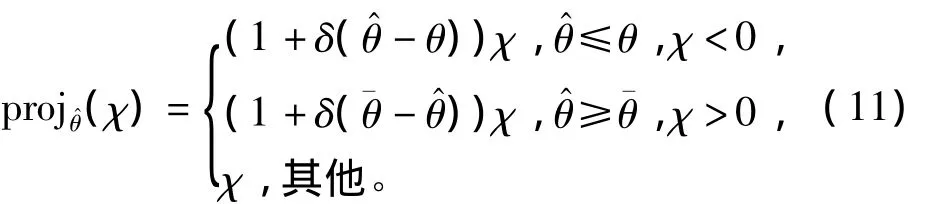
可以看出，所设计的自适应输出反馈控制器包含三部分:用于估计系统状态的高增益观测器(8)、用于反馈的控制器(10)和用于估计参数的参数估计器(9)。而反馈控制器(10)又由两部分组成:确保系统稳定的主反馈部分和用于抵消干扰项d和部分不确定的补偿部分。

所设计的自适应输出反馈控制器中的待定矩阵L，K和PK由下面定理给出。

定理1 选择γ＞1和α＞0，如果存在正定对称矩阵 PL∈R3×3，XK∈R3×3和 QL∈R3×3，矩阵 YL∈R3和 YK∈R1×3以及正数 ε1和 ε2，使得不等式

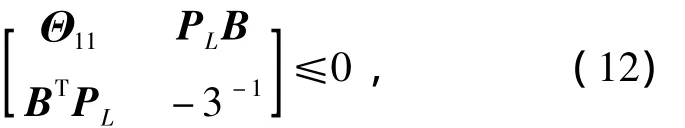
证明 该证明由(P1)和(P2)两部分组成。

(P1)部分:观测器收敛性分析

由式(7)和式(8)，可得

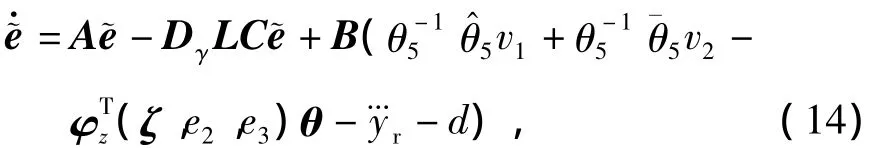
由于z1和 θi(i=1，…，5)有界，容易得出 φ1(z1)，φ2(z1，p)和v2都有界，再根据式(9)和式(11)，可得(i=1，…，5)有界，因此存在常数cηj＞ 0，j=1，2，3，使得‖η1‖≤cη1，‖η2‖≤cη2，|η3|≤cη3。

考虑正定函数V1(ξ)=ξTPLξ，由式(15)，可得

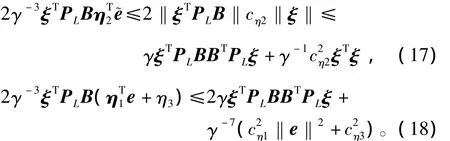
将式(17)和式(18)代入式(16)中，整理得

令YL=PLL，如果不等式(12)成立，则有

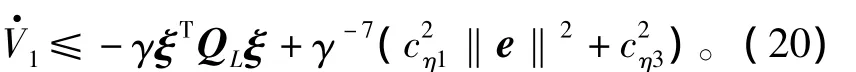
由于QL＞0，γ＞1，因此存在一个有限时间T1，使得当t≥T1时，有

(P2)部分:闭环系统稳定性分析

由系统(7)和控制器(10)，经整理可得到闭环系统为

考虑由式(10)第三个公式定义的v2，以及≥1，可得

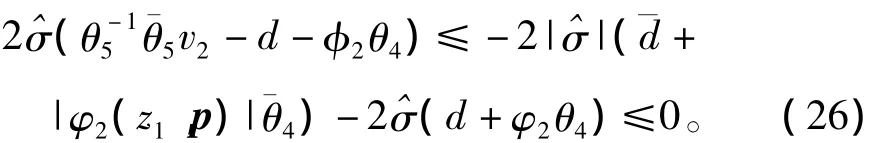
根据由式(11)定义的投影算子，若对未知参数θi的估计为=(βiχi)，i=1，…，5，其中，θi≤θi≤，容易验证

式中:κj=1，j=1，…，4;κ5=＞0。

再将不等式(25)，式(26)和式(28)代入式(24)中，整理可得

显然α1＞0，若选取适当的γ和α使得α'2＞0，由式(32)可以得出，，闭环系统的所有信号是有界的，‖e‖和‖~‖最终收敛到原点的一个由ℓ1决定的邻域内，实际上，最终收敛边界由γ-1决定，选择的γ越大，得到的最终收敛域就越小。

证毕。

由定理1可知，选取的γ越大，系统状态和估计误差的最终收敛域越小，但是，如果可测输出中存在噪声干扰，在高增益观测器中，选取的高增益γ越大，噪声被放大的也越大［13］。因此，在实际过程中，选取的γ值不宜过大。

3 仿真研究

为验证所给出的控制方案的有效性，下面以某650 mm单机架可逆冷带轧机液压伺服位置控制系统为例进行仿真。仿真中所用的主要物理参数为:m=1 500 kg，A1=0.125 6 m2，A2=0.042 2 m2，ks=109N/m，Bp=2.25 ×106N·s/m，w=0.025，kv=1.25 ×10-4m/V，Cd=0.61，βe=7 ×108Pa，ps=24 MPa，pr=1 MPa，Ct=5 ×10-16m5/(N·s)，V10=3.768 ×10-3m3，V20=1.266 ×10-3m3，ρ=850 kg/m3。

仿真中选取的参数为:γ =10，α =209，cη2=102，β1=105，β2=107，β3=104，β4=2 000，β5=0.2。通过求解不等式(12)和(13)，可以解得

利用上面得到的数据，将构造的输出反馈控制器式(8)～式(10)作用到原系统进行仿真，仿真结果如图1～图4所示。

从仿真结果图可以看出，所构造的输出反馈控制器能够保证闭环系统的所有信号有界，系统状态，及其估计值和估计误差都收敛到原点附近的小邻域内。具体地，从图1(a)可以看出，系统跟踪误差在较短的时间内趋向于零，具有较好的跟踪效果。

另外，各参数的估计值(如图2所示)也收敛到其各自的允许范围内，控制输入(如图3所示)和油缸压力(如图4所示)都收敛到其各自的稳定值。仿真结果验证了定理1的结论。

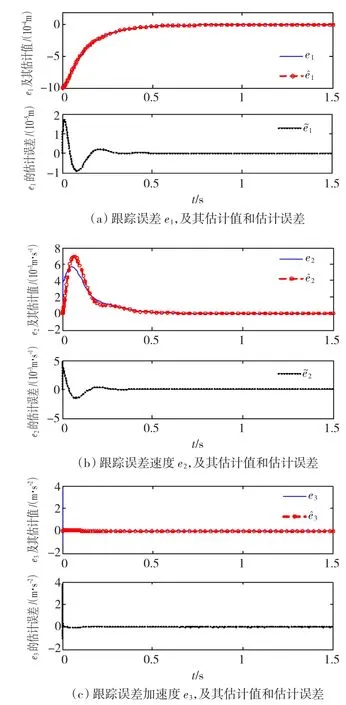
图1 误差模型(7)的系统状态，及其估计值和估计误差Fig．1 System states of Error Model(7)，their estimates and estimation errors

图2 未知参数的估计Fig．2 Estimates of the unknown parameters

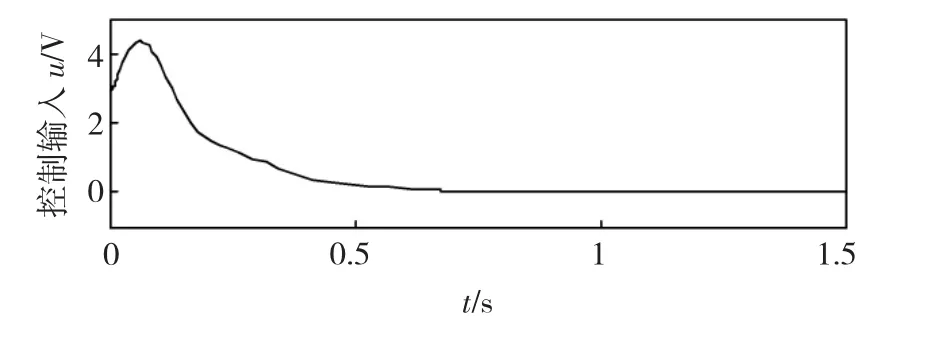
图3 控制输入Fig．3 Control input

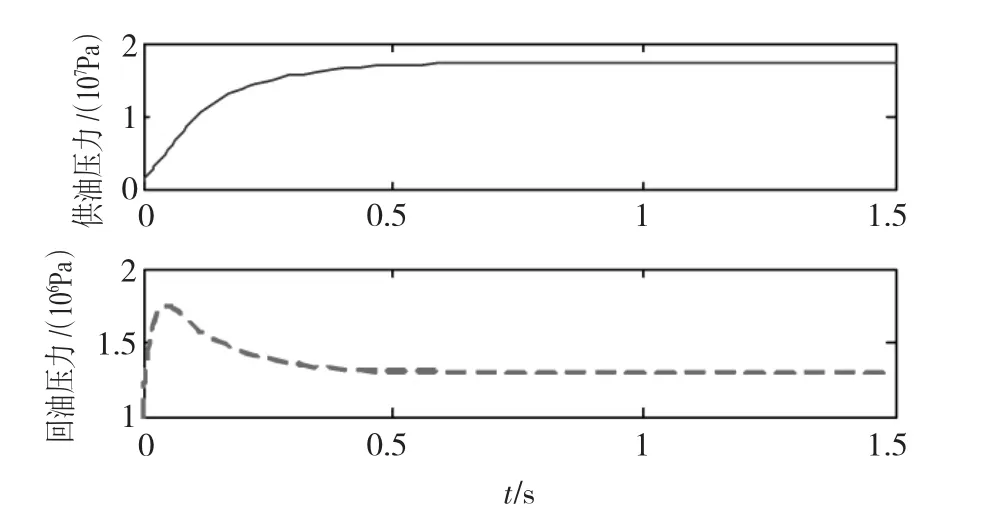
图4 油缸压力Fig．4 Pressure of the cylinders

4 结语

本文针对具有不可测状态、未知参数和非线性的轧机液压伺服位置系统，提出了一种基于高增益观测器和参数估计器的自适应输出反馈控制算法。通过选取适当的参数，系统跟踪误差可以收敛到原点的一个很小的邻域内，邻域的边界依赖于高增益值，并且闭环系统的其他信号都有界。最后，以某650 mm可逆冷带轧机液压伺服位置控制系统为例进行仿真，仿真结果验证了所提出算法的有效性。

［1］YAO Bin，BU Fanping，CHIU George T C.Non-linear adaptive robust control of electro-〛hydraulic systems driven by double-〛rod actuators［J］.International Journal of Control，2001，74(8):761-775.

［2］管成，潘双夏.含有非线性不确定参数的电液系统滑模自适应控制［J］.控制理论与应用，2008，25(2):261-267.

GUAN Cheng，PAN Shuangxia.Sliding mode adaptive control of electro-〛hydraulic system with nonlinear unknown parameters［J］.Control Theory＆ Applications，2008，25(2):261-267.

［3］GUAN Cheng，PAN Shuangxia.Adaptive sliding mode control of electro-〛hydraulic system with nonlinear unknown parameters［J］.Control Engineering Practice，2008，16(11):1275-1284.

［4］方一鸣，王志杰，解云鹏，等.轧机液压伺服位置系统多模型切换滑模变结构控制［J］.电机与控制学报，2010，14(5):91-97.

FANG Yiming，WANG Zhijie，XIE Yunpeng，et al.Sliding mode variable structure control of multi-model switching for rolling mill hydraulic servo position system［J］.Electric Machines and Control，2010，14(5):91-97.

［5］仲伟峰，何小溪.电液位置伺服系统的模糊神经网络控制［J］，电机与控制学报，2007，12(4):478-482.

ZHONG Weifeng，HE Xiaoxi.Fuzzy neural network control of electro-hydraulic position servo system［J］.Electric Machines and Control，2007，12(4):478-482.

［6］赵琳琳，方一鸣，范志远，等.冷带轧机厚控系统自适应鲁棒输出反馈动态控制器设计［J］.控制理论与应用，2008，25(4):787-790.

ZHAO Linlin，FANG Yiming，FAN Zhiyuan，et al.Design of adaptive robust output feedback dynamic controller for thickness control in a cold strip rolling mill［J］.Control Theory＆ Applications，2008，25(4):787-790.

［7］GARIMELLA P，YAO Bin.Nonlinear adaptive robust observer for velocity estimation of hydraulic cylinders using pressure measurement only［C］//ASME 2002 International Mechanical Engineering Congress and Exposition，November 17-22，2002，New Orleans，USA.2002:907-916.

［8］MAKKARAT P，KUNTANAPREEDA S.Observer-based backstepping force control of an electro-hydraulic actuator［J］.Control Engineering Practice，2009，17(8):895-902.

［9］丁玉琴，刘允刚.无未知参数先验信息的非线性自适应观测器设计［J］.控制理论与应用，2008，25(1):27-37.

DING Yuqin，LIU Yungang.Nonlinear adaptive observer design without a prior knowledge on the unknown parameters［J］.Control Theory＆ Applications，2008，25(1):27-37.

［10］DONG Yali，MEI Shengwei.Adaptive observer for a class of nonlinear systems［J］.Acta Automatica Sinica，2007，33(9):1081-1084.

［11］BESANCON G，ZHANG Qinghua，HAMMOURI H.High-gain observer based state and parameters estimation in nonlinear systems［C］//ALLGÖWER F，ZEITZ M.Nonlinear control systems 2004:a proceedings of the 6th International Federal of Automatic Control Symposium，Stuttgart，Germany，September 1-3，2004，Oxford:Elsevier，2005，1:327-332.

［12］FARZA M，M’SAAD M，ROSSIGNOL L.Observer design for a class of MIMO nonlinear systems［J］.Automatica，2004，40(1):135-143.

［13］FARZA M，M’SAAD M，MAATOUG T，et al.Adaptive observers for nonlinearly parameterized class of nonlinear system［J］.Automatica，2009，45(9):2292-2299.

［14］MERRITT H E.Hydraulic control systems［M］.New York:John Wiley and Sons，1967.

［15］LEE K W，KHALIL H K.Adaptive output feedback control of robot manipulators using high-gain observer［J］.International Journal of Control，1997，67(6):869-886.