可调速异步盘式磁力联轴器的转矩计算及其影响因素分析
杨超君, 郑武, 李志宝
(1.江苏大学机械工程学院,江苏镇江 212013;2.上汽通用五菱汽车股份有限公司,广西柳州 545000)
0 引言
可调速异步盘式磁力联轴器是在已有的鼠笼转子磁力联轴器基础上研制出的一种电磁感应磁力联轴器。它研制的目的在于:其一是解决机械联轴器由于直接接触易造成过大的振动,从而可能导致机械联轴器及其相关部件损坏的问题;其二是实现电机的软启动,即低负荷启动、满负荷运行,从而避免电机在负载启动时,转子中可能感应出较大的转子电流而使电机迅速发热,严重时甚至可能烧坏线圈的现象。此外,也可以通过调速装置调节永磁盘和铜盘的气隙长度,实现不同转矩的输出,从而实现速度可调。因此在传送带、升降机、泵、压缩机、离心机、风扇、风箱、破碎机等传动系统中具有很好的应用前景[1-3]。
可调速异步盘式磁力联轴器可实现动力非接触传递,其主要性能指标是传递的转矩,而传递的转矩与其磁场有关,磁场又与一系列构成磁力联轴器的性能参数有关,即磁力联轴器的各参数通过对磁场的影响进而影响转矩的大小。因此,为了磁力联轴器的优化设计,就其结构参数对转矩的影响进行深入研究就显得很有必要。目前,磁场研究中已有一些磁场计算方法[4-6]如磁路法、解析法。但由于可调速异步盘式磁力联轴器内部磁场分布比较复杂,为了计算准确以及得到更详细的计算结果,本文拟采用有限元法对其磁场进行数值计算。这里首先根据可调速异步盘式磁力联轴器的结构建立分析模型,应用三维有限元法对其磁场进行数值计算;然后基于该有限元分析模型,详细的讨论气隙、永磁体厚度、磁极数、从动盘的槽数、槽深以及主动转速等参数对其转矩的影响。
1 基本结构
可调速异步盘式磁力联轴器其结构如图1所示。它是由两个普通的盘式磁力联轴器复合而成。其主动转子上布置有永磁体,轴向磁化且紧密相间排列,如图2所示,而在从动转子上开槽嵌入铜导体,其铜导体内外环用薄环形铜层包起,形成封闭的感应电流回路,如图3所示。可调速异步盘式磁力联轴器主动盘与从动盘不接触,可避免振动的干扰,减小传动部件的损耗,两盘通过气隙磁场相互作用实现转矩的传递。
它的调速工作原理见图1。当转动操作手柄14,通过螺纹传动副17使双推力球轴承13推动右从动盘基体12压缩弹簧9,同时右从动盘基体12推动转动连杆7转动并拉着左从动盘基体6同时压缩弹簧,这样便拉开两个从动盘基体与主动盘基体的距离。当操作手柄反转时,被压缩的弹簧回复,又推动两从动转盘基体6、12向外移动,把距离拉开。通过操作调速装置上手柄可在联轴器工作过程中随时改变从动盘与主动盘间的距离,控制输出功率、转矩的大小,从而实现变速。
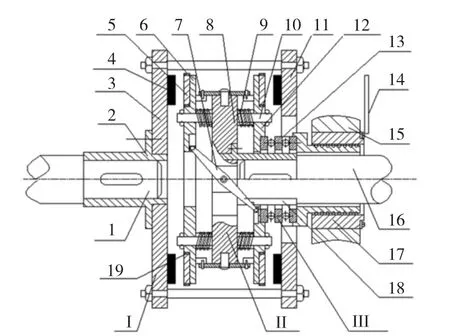
图1 可调速异步盘式磁力联轴器结构图Fig.1 Structure of speed-adjustable asynchronous disk type of magnetic coupling
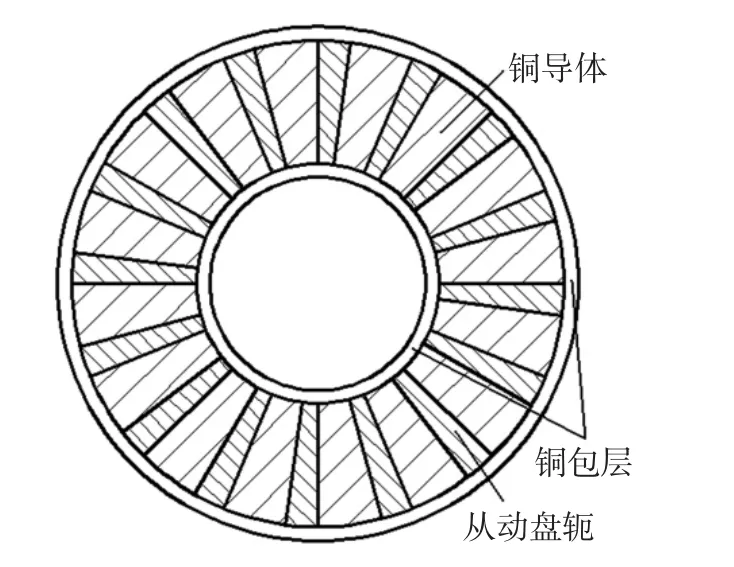
图3 铜导体分布Fig.3 Distribution of copper conductor
可调速异步盘式磁力联轴器实现电机软起动过程为:在启动电机时,可通过调速装置把主、从动盘间的气隙拉到最大,这样电机与负载实现最大分离,电机空载或低负载启动,在电机运行稳定后,再通过调速装置把主、从动盘点的气隙调到预定的位置。这样便避免了电机在负载启动过程中由于转差率过大,感应出很大的转子电流而使电机迅速发热,烧坏线圈的现象。
2 分析模型的建立
磁力联轴器的主磁场为三维轴向磁场,与传统的径向圆柱式磁力联轴器磁场分布不同,因此不能像处理圆柱式磁力联轴器那样,选取联轴器的横截面来建立其二维模型,需建立三维模型才能准确地反映其磁场分布的情况[7-8]。
本文在进行磁场数值计算时,进行一定的假设以简化计算过程:①铁磁材料各向同性,忽略磁滞效应,采用平均磁化曲线;②只考虑模型中与磁性相关的材料,包括主动转盘、从动转盘、永磁体以及铜导体,其余的当作空气处理。
在上述假设的基础上建立有限元几何分析模型如图4所示,图4(a)为分析模型,图4(b)为结构尺寸。其中,δ为气隙长度(mm),h为转子轭铁厚度(mm),h1为槽深(mm),hM为永磁体厚度(mm),R1为永磁体内径,R2为永磁体外径(mm)。
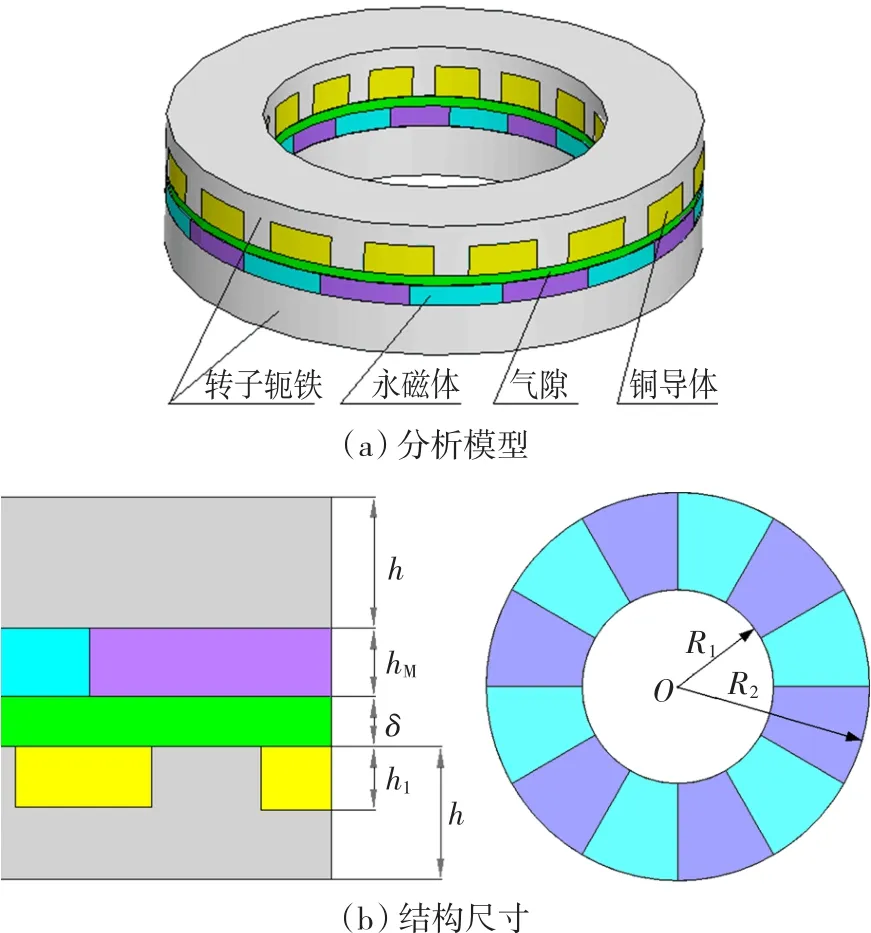
图4 可调速异步盘式磁力联轴器分析模型Fig.4 Analysis model of speed-adjustable asynchronous disk type of magnetic coupling
在分析模型图4(a)中,记整个求解域为Ω,模型的内外侧面为S1,不同介质交界面为S2,铜导体沿从动转子半径方向的侧面为S3,在求解域Ω内求解磁矢位A的数学模型为

式中:β为材料的磁阻率,n为S2或S3的法线方向。对空气,取,其中μ0为空气的磁导率;对钕铁硼材料,取 β≈1/1.099μ0;对铁质材料,由其磁化曲线B=f(H)确定。
磁感应强度B可以由磁矢位A得到

由式(1)求得 A(x,y,z)后,可根据式(2)求得B(x,y,z),从而得到联轴器磁场分布。求得联轴器磁场分布后,即可求得磁力联轴器的转矩为

式中:V为主、从动盘间气隙体积(mm3);r1、r2为铜导体内、外半径(mm)。
3 磁场计算及分析
可调速异步盘式磁力联轴器的气隙为平面型,气隙磁场为轴向,其各内部磁场呈复杂的三维分布且各部分磁密分布不均匀,不同半径处磁路长度不同,其磁场计算比同轴式磁力联轴器复杂。为了精确计算其内部磁场,利用有限元软件ANSOFT对其进行分析。
设磁力联轴器在一定的外形尺寸下的分析模型参数为:磁极数为18,槽数16,铜导体为扇形结构,应用有限元软件Maxwell 3D进行分析。
图5、图6分别显示了磁力联轴器在静态和瞬态下磁场分布,从两图中可以看出其磁力线走向一致,但大小并不一致。原因是:静态时磁力联轴器没有相对转速,其磁场都是由永磁体提供,而在磁力联轴器负载时,由于主、从动转子存在转速差,铜导体切割磁力线,由此产生会有感应电流产生,从而产生一个感应磁场,此感应磁场与永磁体提供的磁场相互叠加。

图5 静态气隙处磁场分布Fig.5 Field distribution on static air gap
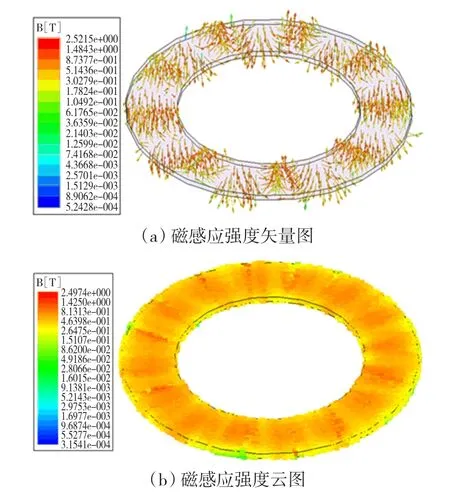
图6 瞬态气隙处磁场分布Fig.6 Field distribution on transient air gap
4 传动性能的影响因素分析
4.1 气隙长度对转矩的影响
本文联轴器气隙长度是指主、从动盘间的单边气隙长度。以18极为例,保持其他尺寸不变,得到磁力联轴器在不同气隙长度下转矩随时间的变化曲线如图7,取0.01 s后转矩的平均值,作磁力联轴器转矩与气隙长度的关系曲线如图8。
从图7和图8中可以看出转矩随气隙长度的增加而减小。原因在于联轴器中气隙的磁阻要比主、从动转盘的磁阻大得多,磁势有很大部分消耗在气隙中,气隙长度过大,则消耗在气隙中的磁势必定增加,使得气隙磁密减小,从而导致转矩降低。理论上,在设计中应尽量减小气隙长度,但在实际设计中,减小气隙长度又受很多情况的限制,如装配时的同轴度、旋转时的振动以及转矩脉动情况等[9]。因此,联轴器气隙长度的选择应综合考虑,一般取5~10 mm。

图7 不同气隙长度时转矩随时间变化曲线Fig.7 The torque curve change with time with different air gap
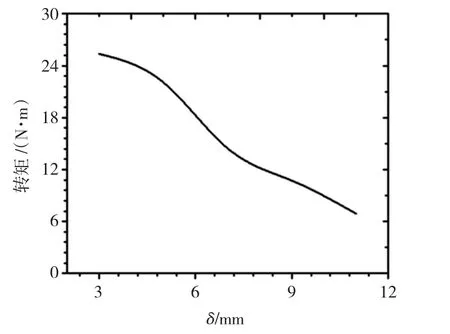
图8 转矩与气隙长度关系曲线Fig.8 The curve of torque and air gap changing
4.2 永磁体磁极数对转矩的影响
改变联轴器磁极数,保持其他尺寸不变,得到联轴器不同永磁体磁极数时转矩随时间变化曲线如图9,取0.01s后转矩的平均值,作磁力联轴器转矩与永磁体磁极数的关系曲线如图10。
从图10中可知,在一定范围内,随着磁极数增加,转矩增大,而当磁极数增加到一定数目后,转矩开始降低,且在18极时输出转矩达到最大约为20 N·m。因为由静磁能表达式[10]可知,N、S极每变化一次,静磁能的存储便增加一次,故磁极数越多就越有利于静磁能的存储;但磁极数过多,不同磁极接触就越多,漏磁也越大,使得气隙中的磁密减小,传递的转矩降低;同时磁极数目太多并使得每一块永磁体的尺寸减小,过小的尺寸对加工以及装配工艺带来困难。因此,在磁极数选择上,应综合考虑气隙磁密、漏磁大小以及永磁体加工、安装的工艺,本文联轴器选择18极为佳。
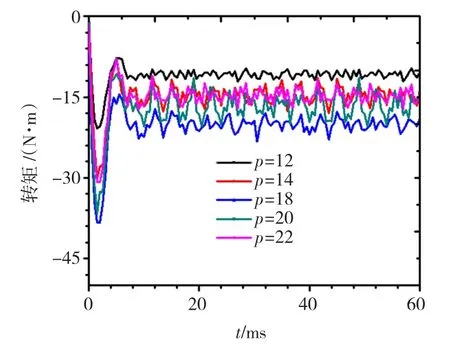
图9 不同永磁体磁极时转矩随时间变化曲线Fig.9 The curve of torque with time changing with different magnetic poles

图10 转矩与永磁体磁极数关系曲线Fig.10 The curve of torque and magnetic poles
4.3 永磁体厚度对转矩的影响
固定气隙δ、保持联轴器其他参数不变,分析转矩与永磁体厚度关系曲线。图11为不同永磁体厚度磁力联轴器转矩随时间的变化曲线,取0.01 s后转矩的平均值,作磁力联轴器转矩与永磁体厚度的关系曲线如图12。
从图12中可以看出增大永磁体厚度hm,可以提高转矩。这是因为永磁体在磁路中提供磁势,永磁体越厚则提供的磁势就越大,磁路中的气隙磁密就越强,但永磁体厚度的增大并不能无限提高转矩的大小。随着永磁体厚度hm的增大,转矩为一上升的曲线,但随着永磁体厚度达到10 mm后,随着hm继续增大,转矩增加变慢。原因是在高矫顽力的永磁体中,永磁体内部的磁阻非常大,随着永磁体厚度的增加,虽磁势增加了,但磁阻、漏磁也相应的增加,当永磁体厚度增大到一定厚度时,所增加的磁势大部分消耗在增加的磁阻、漏磁上,而对转矩的贡献很少。因此在设计中选择永磁体厚度不宜太厚,以免永磁体材料利用率低。
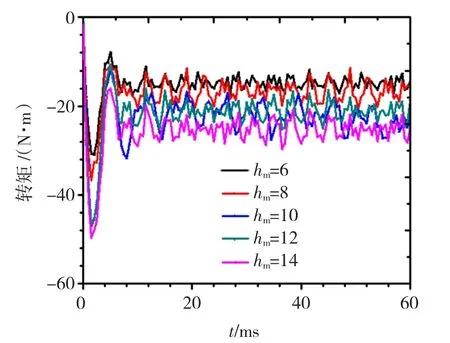
图11 不同永磁体厚度时转矩随时间变化曲线Fig.11 The curve of torque with time changing with different thickness of the permanent magnet
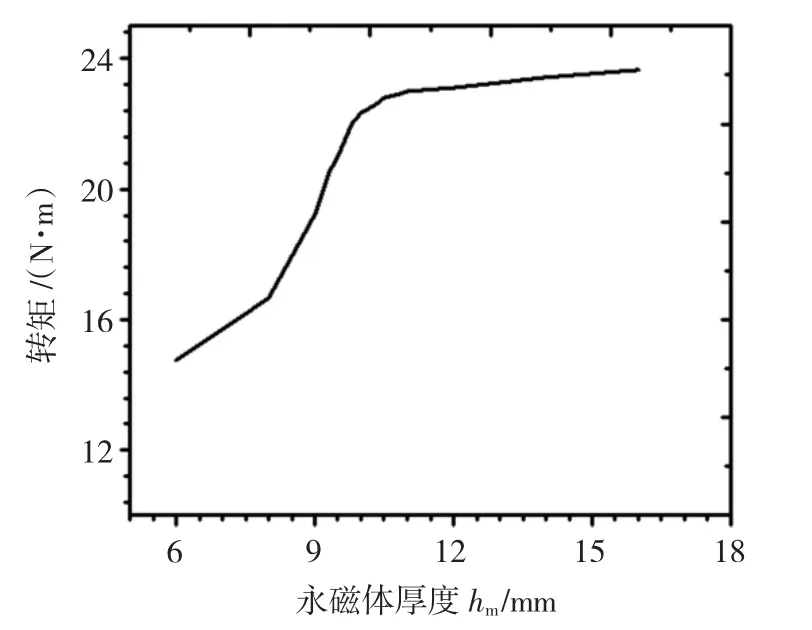
图12 转矩与永磁体厚度关系曲线Fig.12 The curve of torque and thickness of the permanent magnet
4.4 槽数对转矩的影响
保持联轴器其他参数不变,只改变从动转子上槽数。图13显示了不同槽数的磁力联轴器转矩随时间的变化曲线,取0.01 s后转矩的平均值,作磁力联轴器转矩与槽数的关系曲线如图14。从图14中可以看出,随着槽数的增加,转矩先增大后减小,在16槽时达到最大,可达21 N·m左右。其原因是槽数增大,相当于从动转子盘齿部面积减小,齿部磁密增大。但随着槽数继续增大时,齿部面积过小,引起从动盘齿部磁密饱和,使得齿部磁密减小,转矩降低。
图15为槽数18槽,且与主动盘上永磁体数目相等时,磁力联轴器转矩随时间变化的曲线。从图中可见,转矩随时间成类似正弦曲线关系变化,与图13中的转矩变化曲线有很大的区别,其原因是:对于槽数和磁极数相等的磁力联轴器,当主动转子旋转时,处于永磁体磁极中心处的从动转子齿与永磁体间的磁导几乎不变,因此这些转子齿周围的磁场也基本不变,而与每个永磁体两侧面对应的由一个或两个从动转子齿所构成的小段封闭区域内,磁导变化很大,引起磁场储能变化,从而产生了较大的齿槽转矩[11-12]。齿槽转矩虽然并不影响平均转矩的输出,但它却能造成磁力联轴器较大的振动和噪音,因此应减量削弱,因此在联轴器设计中,磁极数和槽数不能相等。
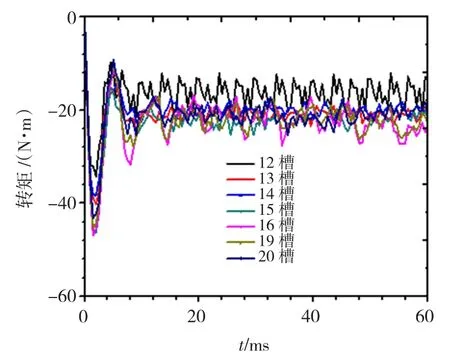
图13 不同槽数时转矩随时间变化曲线Fig.13 The curve of torque with time changing with different slots number
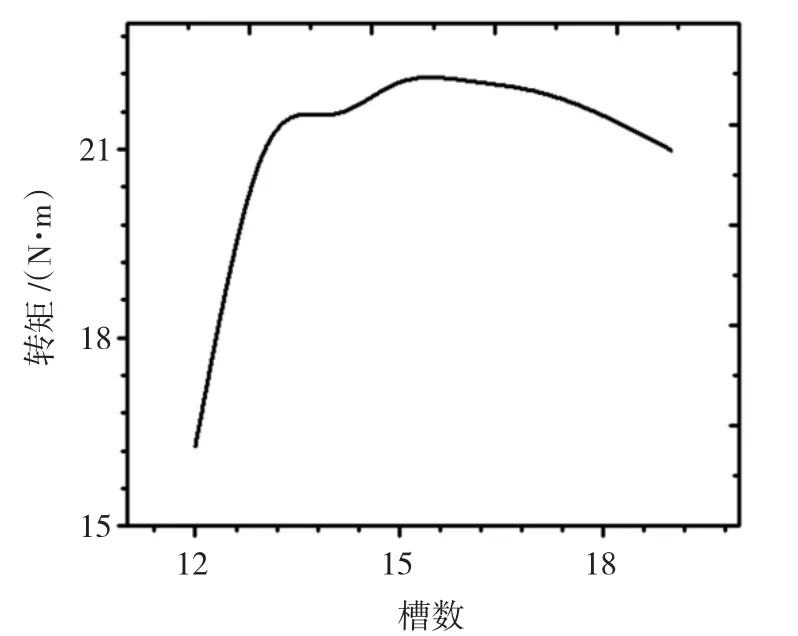
图14 转矩与槽数的关系曲线Fig.14 The curve of torque and the number of slots
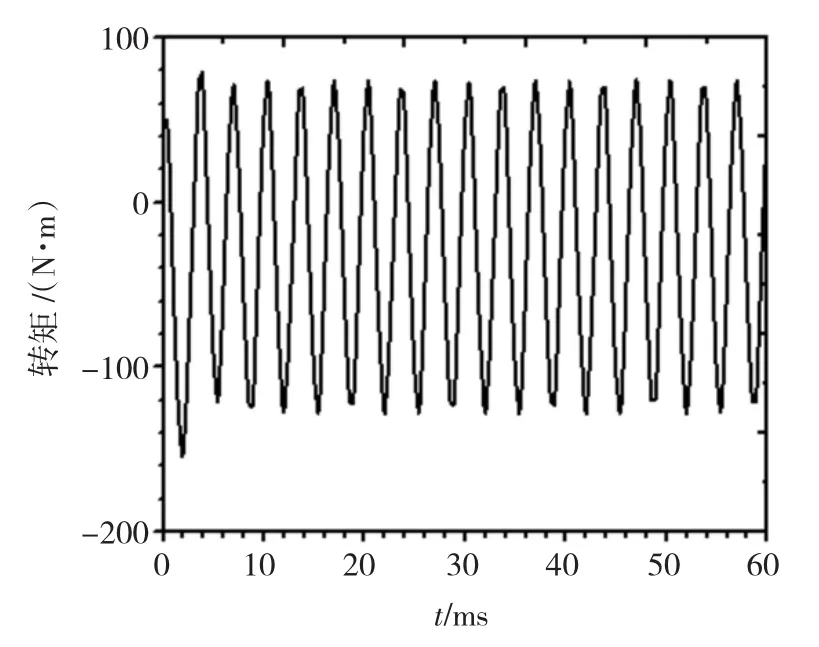
图15 槽数为18时转矩随时间变化曲线Fig.15 The curve of torque with time changing when the number of slots is 18
4.5 槽深对转矩的影响
保持联轴器其他参数不变,只改变从动转子上的槽深,图16为不同槽深磁力联轴器转矩随时间的变化曲线,取0.01 s后转矩的平均值,作磁力联轴器转矩与槽深的关系曲线如图17。
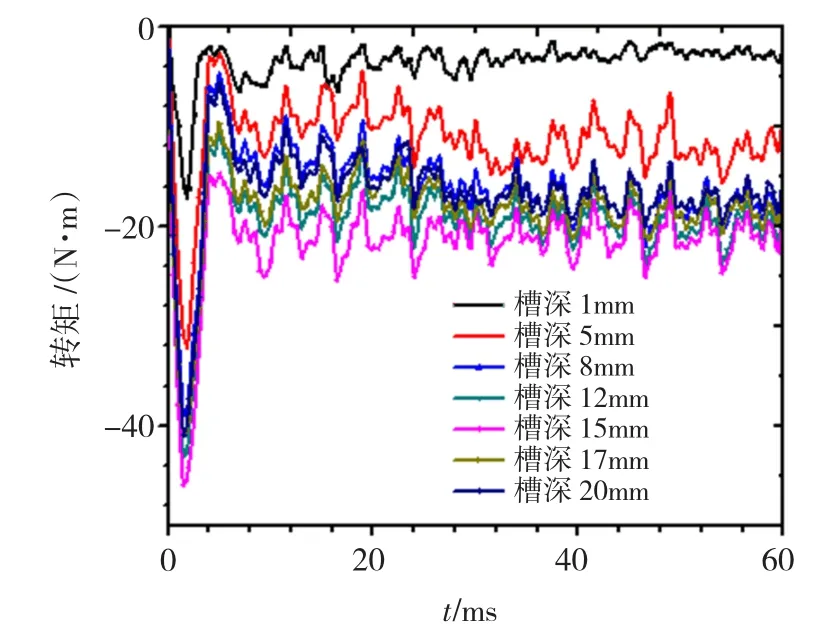
图16 不同槽深时转矩随时间变化曲线Fig.16 The curve of torque with time changing with different slot depth
从图17中可以看出,随着槽深的增加,转矩先增大后减小,在槽深为15 mm时达到最大约为20 N·m。其原因是:槽越深即从动转子铜导体在轴向方向就越长,集肤效应程度越明显,感应电流集中分布在铜导条的上部,使得从动转子电阻增大,转子漏抗减小,从而使得转矩得到提高。但随着槽深继续增大时,从动盘轭部导磁体积减小,引起从动盘轭部磁密饱和,气隙磁密减小,使得转矩变小。

图17 转矩与槽深关系曲线Fig.17 The curve of torque and slot depth
4.6 主动转子转速对转矩的影响
根据以上分析的较佳参数,建立分析模型。图18显示了主动转速与输出转矩的关系。从图中可见,转矩随着主动转速先增大后减小。其原因是:在主动转速增大时,输出的功率增大,转矩增大,直到磁力联轴器输出功率达到最大值,不再变化时,再增大主动转速,主、从动转子转速差变大,在铜导体上产生的感应电动势增大,此时,铜导体上功率损耗增加,又使得输出转矩变低。此曲线类似于电机的机械特性曲线,因此可依据此曲线根据不同的转矩输出选择相应的电机转速,也可作为磁力联轴器调速的依据之一。
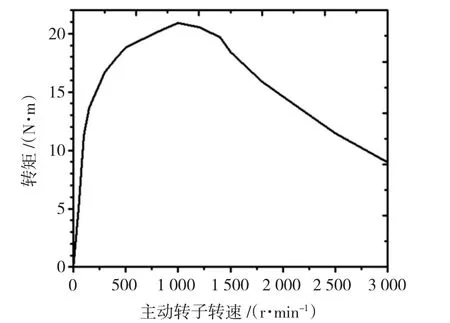
图18 转矩与主动转速的关系曲线Fig.18 The curve of torque and the speed of the drive wheel
5 结论
通过对可调速异步盘式磁力联轴器的静态和瞬态分析,获得了磁力联轴器不同参数对输出转矩的影响规律,研究的结论给该类磁力联轴器的优化设计提供了很好的依据,主要结论如下:
1)增加气隙长度会降低联轴器的转矩。在选取气隙长度时应综合考虑装配时的同轴度、旋转时的振动以及转矩脉动情况,一般取5~10 mm。
2)在一定的范围内,增大联轴器的磁极数,转矩增大,在18极时转矩达到最大值约20 N·m,随着磁极数继续增大,转矩降低。
3)增加永磁体厚度可以增大转矩,但不能无限增大,当永磁体厚度增大到10 mm后,转矩曲线的斜率逐渐变小,增加变慢,永磁体利用程度降低,永磁材料浪费较大。
4)随着槽数的增加,转矩先增大后减小,在16槽时达到最大,可达21 N·m左右。随着槽深的增加,转矩先增大后减小,在槽深为15 mm时达到最大约为20 N·m。
5)转矩随着主动转速先增大后减小,变化曲线类似于电机的机械特性曲线,因此可依据此曲线根据不同的转矩输出选择相应的电机转速,也可作为磁力联轴器调速的依据之一。
6)在设计时从动盘时,其槽数不能和永磁体的磁极数相等,以免出现较大的齿槽转矩造成磁力联轴器有较大的振动和噪音。
[1]杨超君,王晶晶,顾红伟,等.鼠笼转子磁力联轴器空载气隙磁场有限元分析[J].江苏大学学报:自然科学版,2009,31(1):68 -71.
YANG Chaojun,WANG Jingjing,GU Hongwei,et al.Finite element analysis of no-load air gap magnetic field in squirrel cage rotor of asynchronous magnetic coupling[J].Journal of Jiangsu University:Natural Science Edition,2009,31(1):68 -71.
[2]杨超君,郑武,李直腾.可调速式磁感应联轴器[P].中国:200910263064.
[3]付媛,罗应立,陈伟华,等.自起动永磁电动机的稳态转矩波动研究[J].电机与控制学报,2010,14(11):1 -6.
FU Yuan,LUO Yingli,CHEN Weihua,et al.Research on torque fluctuation of line-start PM motor based on time-step finite element method[J].Electric Machines and Control,2010,14(11):1 -6.
[4]杨超君,蒋生发.反求设计技术在新型电磁感应式磁力联轴器研制中的应用[J].机械设计与研究,2002,18(4):64 -65.
YANG Chaojun,JIANG Shengfa.Application of reverse engineer technology in design of a new-type induetion magnetic coupling[J].Machine Design and Research,2002,18(4):64 - 65.
[5]AMATIL N,TONOLIL A,CANOVA A,et al.Dynamic behavior of torsional eddy-current dampers:sensitivity of the design parameters[J].IEEE Transactions on Magnetics,2007,43(7):3266 -3277.
[6]孔晓光,王凤翔,徐云龙,等.高速永磁电机铁耗的分析和计算[J].电机与控制学报,2010,14(9):26 -30.
KONG Xiaoguang,WANG Fengxiang,XU Yunlong,et al.Analysis and calculation of iron losses of high-speed permanent magnet machines[J].Electric Machines and Control,2010,14(9):26 -30.
[7]YANG Chaojun,LI Quanwen,MA Hongliang,et al.Numerical calculation of the outer thickness of double-solid rotor asynchronous permanent magnetic coupling by finite element method[J].Int.J.Materials and Product Technology,2010,39,(3/4):383-390.
[8]李军,罗应立,刘晓芳,等.低速永磁电动机转矩特性的三维有限元分析[J].电机与控制学报,2011,15(2):13-19.LI
Jun,LUO Yingli,LIU Xiaofang,et al.Analysis of low-speed PM-motor’s torque characteristics by 3D-FEM[J].Electric Machines and Control,2011,15(2):13 - 19.
[9]ZHU Z Q,RUANGSINCHAIWANICH S,ISHAK D,et al.Analysis of cogging torque in brushless machines having no uniformly distributed stator and stepped rotor magnets[J].IEEE Transactions on Magnetics,2005,41(10):3910 -3912.
[10]钟文定.铁磁学[M].北京:科学出版社,1987:54-72.
[11]程树康,宫海龙,柴凤,等.永磁轮毂电机齿槽转矩研究.中国电机工程学报[J],2009,29(30),47 -51.
CHENG Shukang,GONG Hailong,CHAI Feng,et al.Study on cogging torque of permanent magnet in-wheel motor[J].Proceedings of the CSEE,2009,29(30):47 -51.
[12]王道涵,王秀和,丁婷婷,等.基于磁极不对称角度优化的内置式永磁无刷直流电动机齿槽转矩削弱方法[J].中国电机工程学报,2008,28(9):66 -70.
WANG Daohan,WANG Xiuhe,DING Tingting,et al.Optimization for the asymmetric angles of magnetic pole to reduce cogging torque in inner-buried PM brushless DC motors[J].Proceedings of the CSEE,2008,28(9):66 -70.

