永磁同步电机转子初始位置的检测方法

王冉珺， 刘恩海

(1．中国科学院光电技术研究所，四川成都 610209;2．中国科学院 研究生院，北京 100039)

0 引言

在永磁同步电机高性能控制系统中，若在不明确初始位置条件下启动电机，则会出现短暂的转子反转现象，甚至导致启动失败［1］。由于绝对式编码器存在成本偏高，体积较大等问题使得其应用受限，现有控制系统偏重于使用增量式编码器或采用无位置传感器控制，在其控制系统中都需要准确知道转子的初始位置。

目前，电机转子位置检测有两种方法［2］:一种是利用电机的反电动势，通过检测三相绕组的电压或者电流来计算转子位置;另一种是利用电机的空间凸极效应，通过向绕组注入短暂的电压信号，检测其响应电流来计算转子位置。由于反电动势的幅值是跟转速成正比的，并受系统非线性开关产生的噪声影响，在转子静止的时候，无法检测出其初始位置［3］。向电机注入幅值恒定、方向不同的系列脉冲［2－6］，通过比较响应电流大小可以获得转子初始位置，但电机很容易受注入电压的影响发生转动，其检测时间也过长;基于注入高频电压进行初始位置检测的已有方法［6－11］，需要知道电机的相应参数和使用额外的观测器，或利用外差法、锁相环法等算法来提取含有转子位置信息的电流相位序列，算法都较复杂，不便于实际应用;通过检测高频响应电流的幅值也可以估算初始位置［12］，但在对电流幅值进行反正弦查表运算前，需减去直流偏置分量，计算该分量需事先知道电机的自感系数。

针对以上问题，本文提出了一种基于旋转的高频电压注入检测初始位置的方法。通过注入旋转的高频矢量，利用凸极效应，对高频响应电流经行解调、滤波和最小二乘法拟合处理后，即可获得转子的初始位置。然后再根据定子铁心磁路饱和差异，判定永磁体的N/S极。实验结果表明，该方法不依赖电机参数，不需要额外的硬件，高频信号注入期间转子不发生偏移，算法简单，易于实现，从而保证了电机的可靠启动。

1 初始位置检测原理

1.1 高频电压激励下的数学模型

在两相旋转dq坐标系中，定子电压方程为

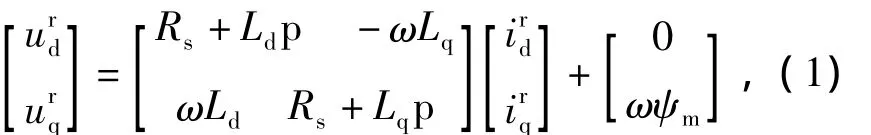
式中:、和分别表示定子电压和电流分量;上角标r表示在两相旋转坐标系下;Rs和L分别为电阻、电感;p为微分算子;ω为转子的电角速度;ψm为永磁体磁链。由于转子初始位置检测是在电机静止的时候，所以ω=0，并且当注入高频信号，高频感抗远大于定子绕组的阻抗，因此可忽略定子绕组上的电阻压降。故定子电压方程简化为

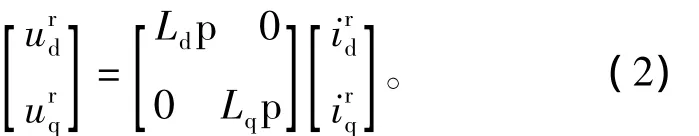
注入的高频信号的电压表达式为

转换到两相旋转坐标系下的电压表达式为

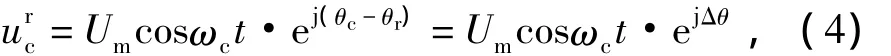
式中u'd、u'q分别表示向估计的直轴和交轴坐标系注入高频电压;如图1所示表示在两相旋转坐标系下注入的电压矢量;Um、ωc分别为注入高频信号的幅值和频率;θc为估计的d＇轴与α轴之间的夹角;θr为d轴与α轴之间的夹角，即永磁体N极与α轴之间的夹角，θ=θc－θr。

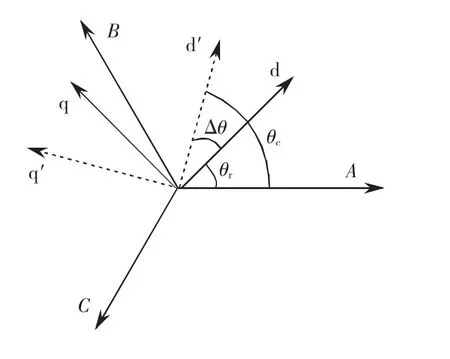
图1 估计坐标轴的定义Fig．1 Definition of estimated coordinates

由式(2)和式(4)可以求出两相旋转坐标系下定子电流矢量为

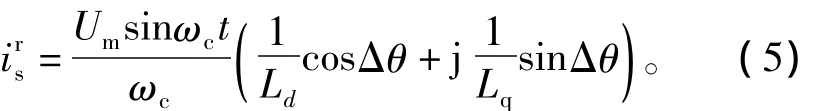
其在两相静止坐标系下的表达式为

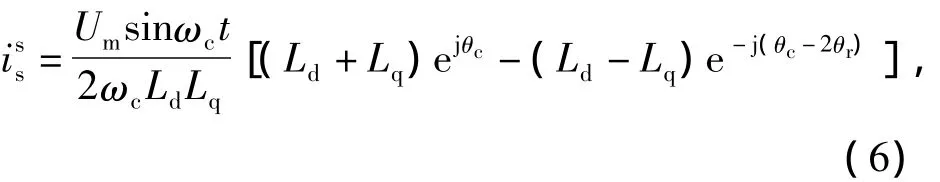
式中上角标s表示在两相静止坐标系下。可以看出定子电流的幅值受到转子位置θr的调制，为了获得θr的信息，对响应的高频定子电流作如图2的处理。

得到响应电流iθ的表达式为

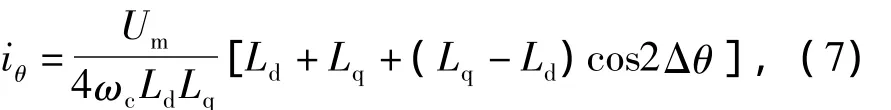
式中Um、ωc、Lq、Ld都是确定值，对于凸极电机来说，由于其结构存在凸极性，故Lq＞Ld，而对于隐极电机，在电机设计中，通常使主磁路在空载条件下已处于基本饱和状态，故其存在饱和性凸极，也有Lq＞Ld，则式(1)简化为

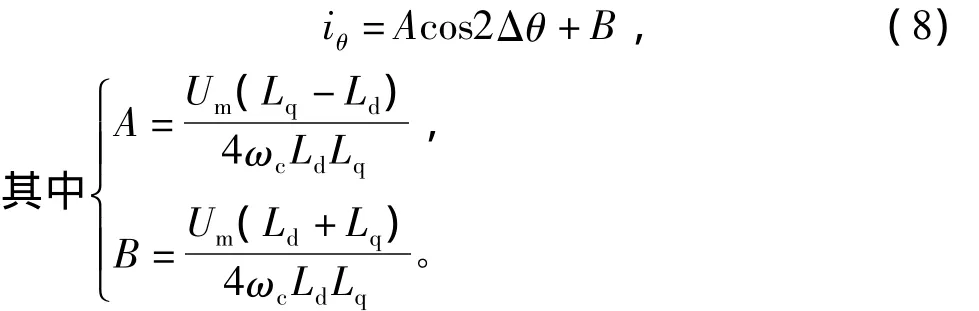
故iθ可以表示为一个受2θ调制的正弦信号叠加了一个直流分量，当θ=0或π时，iθ达到最大值，通过不断地改变估计位置 θc，可以测出iθ变化趋势，就可以计算出永磁体的空间位置。为了获得更高的估算精度，对采样计算出的iθ按式(8)的表达式进行基于最小二乘的拟合，计算出波峰值，便可获得初始位置的角度。

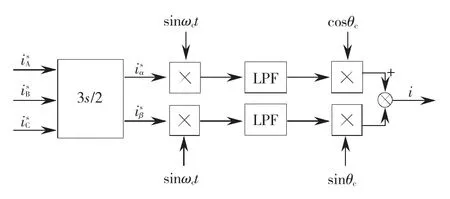
图2 高频电流信号处理过程Fig．2 The signal processing of high frequency current

1.2 转子极性的检测

通过最小二乘拟合求出来的转子位置角度可能为θr，也可能为θr±π。为了解决此问题，可利用磁路的饱和效应检测出永磁体的N极。当三相绕组合成的电流矢量方向和d轴方向一致时，绕组磁势起增磁作用，加重d轴主磁路的饱和，导致d轴电感下降;当三相绕组合成的电流矢量方向和d轴方向相反时，会使主磁路饱和程度减弱，d轴电感随之上升，而电流矢量方向对q轴电感几乎不产生影响。

设θ'为依据上节原理求出的拟合角度值，向θ'方向注入高频信号，记此时计算出的iθ幅值为|I1|，而向θ'+π方向注入高频信号计算出的iθ幅值记为|I2|，当|I1|＞ |I2|时，表明检测出的 θ＇即为转子的实际位置，当|I1|＜|I2|时，θ'+π或者θ'－π才为转子的实际位置。

2 仿真结果

为了验证所提出的转子初始位置检测方法的准确性，本文在Matlab/SIMULINK平台上对不同电机模型进行了初始位置检测仿真实验。实验要注意选择注入的高频矢量的频率，若是频率太低，由式(1)可知，定子绕组阻抗压降所占的比重增加，不能对检测数学模型进行简化，导致结果出现较大误差;若频率太高，会混淆逆变桥的开关频率，并且感抗的增加会造成电流响应过弱，既影响饱和凸极效应，又不利于电流信号的采集。综合考虑，本系统高频信号注入频率选择800 Hz，满足初始位置检测的需求。

图3所示为电流iθ响应波形，其注入的高频矢量幅值均为30 V，频率为800 Hz，对应的电机参数为:定子电阻Rs为0.6 Ω，直轴电感Ld为13.5 mH，交轴电感Lq为15.5 mH，极对数为4。

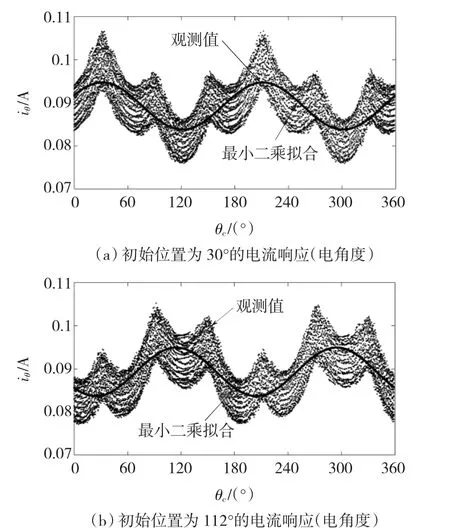
图3 初始位置检测仿真结果Fig．3 The simulation result of initial rotor angle detection

图3(a)转子实际电角度位置为30°，拟合出的表达式为

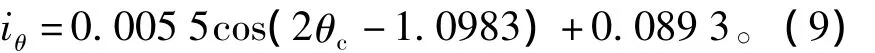
通过极性检测后计算出转子的角度为31.46°，误差为1.46°。

图3(b)对应的转子实际电角度位置为112°，拟合出的表达式为

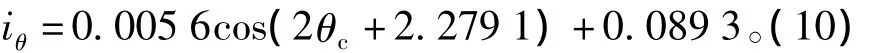
通过极性检测后计算出转子的角度为114.71°，误差为 2.71°。

从仿真结果中可以看出，该方法不需要依赖电机的参数便可估算出的转子角度;另外，由于在仿真中忽略了摩擦力对转子的影响，所以很微小的电流也会带来转子的微小转动，造成电机的气隙磁场发生了改变，导致了电流响应出现非正弦化的表现，如图3所示，出现多个波峰，如果此时用电流响应的最大值去匹配检测的角度，就会带来较大的误差，而用最小二乘方法对数据进行拟合，则可以最大化还原电流响应变化的趋势，可以减小转子微小转动带来的误差影响。

3 实验结果

实验的硬件平台采用DSP作为控制核心，利用外置编码器来验证初始位置估算的精确度，选用的伺服电机为表贴式永磁同步电机，其参数为:额定电压200 V，额定电流5 A，额定转速2 000 r/min，额定功率750 W，额定3.57 N·m，极对数为4。

在仿真的理想环境中，电流响应的值多小都可以精确的获得，但在实际系统中，受到电流采集系统的影响，必须考虑注入高频信号的幅值问题。如果注入的幅值太小，一方面会导致响应电流值较小，电流采样难度增加并易于受外界干扰信号影响，另一方面，对d轴的磁链可能会未充分饱和，影响极性的判断和隐极电机极性的检测;如果注入的幅值太大，则会引起转子发生转动。在合适的幅值选取范围内，由于对注入信号的幅值进行了调制，在仿真中出现的电机转子微小转动都会被实际系统中的摩擦力所克服，转子保持不动。综合考虑，本系统选取的注入高频信号幅值为25 V，频率为800 Hz。

图4为转子实际停在62.58°时，通过采集到的两相电流计算出的响应电流iθ观测值及采用最小二乘方法拟合出的波形图，拟合出的表达式为

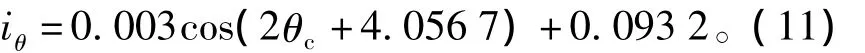
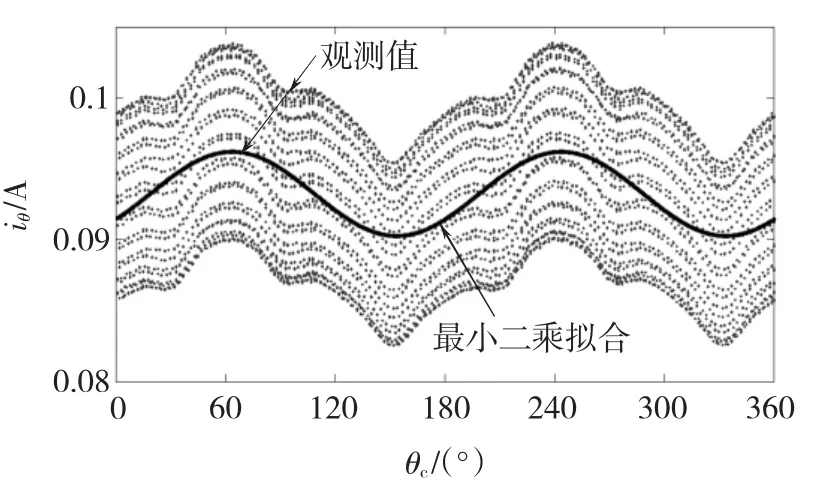
图4 转子在62．58°时的电流响应Fig．4 Current response when the rotor position is 62．58 elec．deg

通过极性检测后计算出转子的初始角度为63.78°，误差为1.2°。由图可以看出，在转子没有发生转动的情况下，电流响应也不为正弦曲线，这是由于电机气隙磁场本身非正弦分布，存在一定的缺陷，另外注入不同方向的电压矢量，实时地改变着磁路的饱和程度，加重或减小了饱和性凸极效应的影响，使得电流响应曲线非正弦化。

图5所示为360°电角度周期范围内实际角度与估计角度对比结果及误差，图5(a)和图5(b)横轴均表示转子的实际值，图5(a)的纵轴表示转子估算值，图5(b)的纵轴表示转子估算值与实际值之间的误差，从图中可以看出，估计的结果较好，平均检测误差为3.33°，最大检测误差为8.45°，在该误差范围内，完全满足永磁同步电机的启动需求。产生误差的主要原因包括:电流采集系统采样误差、编码器的定位误差、电机本体气隙磁场结构不对称和不同位置饱和程度不同带来的误差等。

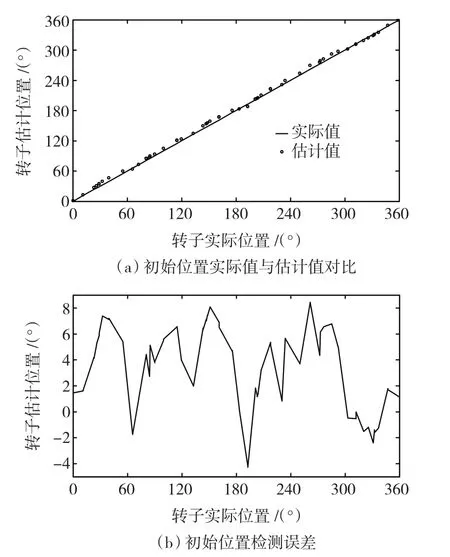
图5 初始位置检测实验结果及误差Fig．5 The experimental result and error of initial rotor angle detection

4 结论

本文提出了一种永磁同步电机初始位置检测的方法，并从理论、仿真、实验三个方面进行分析和研究，结果表明:该方法向电机注入旋转的高频电压，利用高频响应电流来进行初始位置检测，克服了依赖电机参数或需要额外的硬件等缺点，算法易于实现，是一种鲁棒性较好的方法。仿真和实验证明电机转子在检测过程中不发生移动，检测平均误差为3.33°，最大误差为8.45°，满足永磁同步电机平稳、可靠启动的要求。

［1］ISHIDUKA N，YOSHIZAKI K，KOMATSUZAKI A，et al．Esti-mation of initial rotor position for slotless PM motor［C］//International Symposium on Power Electronics，Electrical Drives，Automation and Motion，June 11 － 13，2008，Ischia，Italy．2008:1229－1232．

［2］SUGAWARA J，KAIMORI T，NISHIKATA S．A novel and simple initial rotor position detecting method for PMSMs［C］//Sixth International Conference on Power Electronics and Drive，November 28-December 01，2005，Kuala Lumpur，Malaysia．2006:612－617．

［3］BOUSSAK M．Implementation and experimental investigation of sensorless speed control with initial rotor position estimation for interior permanent magnet synchronous motor drive［J］．IEEE Transactions on Power Electronics，2005，20(6):1413 －1422．

［4］贾洪平，贺益康．基于高频注入法的永磁同步电动机转子初始位置检测研究［J］．中国电机工程学报，2007，27(15):15－20．

JIA Hongping，HE Yikang．Study on inspection of the initial rotor position of a PMSM based on high-frequency signal injection［J］．Proceedings of the CSEE，2007，27(15):15－20．

［5］TURSINI M，PETRELLA R，PARASILITI F．Initial rotor position estimation method for PM motors［J］．IEEE Transactions on industry Applications，2003，39(6):1630 －1640．

［6］JEONG Y，LORENZ R D，JAHNS T M，et al．Initial rotor position estimation of an interior permanent-magnet synchronous machine using carrier-frequency injection methods［J］．IEEE Transactions on Industry Applications，2005，41(1):38 －45．

［7］廖勇，沈朗，姚骏，等．改进的面贴式永磁同步电机转子初始位置检测［J］．电机与控制学报，2009，13(2):203－207．

LIAO Yong，SHEN Lang，YAO Jun，et al．Initial rotor position detection for surface mounted PMSM based on rotating high frequency signal injection［J］．Electric Machines and Control，2009，13(2):203－207．

［8］KIM H，HUH K K，LORENZ R D，et al．A novel method for initial rotor position estimation for IPM synchronous machine drives［J］．IEEE Transactions on Industry Applications，2004，40(5):1369－1378．

［9］周元钧，蔡名飞．改进的永磁同步电机转子初始位置检测方法［J］．电机与控制学报，2010，14(3):68－72．

ZHOU Yuanjun，CAI Mingfei．Initial rotor position inspection of PMSM based on rotating high frequency voltage signal injection［J］．Electric Machines and Control，2010，14(3):68 －72．

［10］HOLTZ J．Acquisition of position error and magnet polarity for sensorless control of PM synchronous Machines［J］．IEEE Transactions on Industry Applications，2008，44(4):1172 －1180．

［11］王高林，杨荣峰，于泳，等．内置式永磁同步电机转子初始位置估计方法［J］．电机与控制学报，2010，14(6):56－60．

WANG Gaolin，YANG Rongfeng，YU Yong，et al．Initial rotor position estimation for interior permanent magnet synchronous motor［J］．Electric Machines and Control，2010，14(6):56 －60．

［12］万山明，吴芳，黄声华．基于高频电压信号注入的永磁同步电机转子初始位置估计［J］．中国电机工程学报，2008，28(33):82－86．

WAN Shanming，WU Fang，HUANG Shenghua．Initial rotor position estimation of permanent magnet synchronous motor based on high frequency voltage signal injection method［J］．Proceedings of the CSEE，2008，28(33):82－86．