永磁交流伺服系统机械谐振成因及其抑制
杨明, 胡浩, 徐殿国
(哈尔滨工业大学电气工程系,黑龙江哈尔滨 150001)
0 引言
伺服驱动系统的机械传动部分经常使用传动轴、变速器、联轴器等传动装置连接电机和负载,而实际传动装置并不是理想刚体,存在一定的弹性,通常会在系统中引发机械谐振。机械振荡除了会发出声学噪声形成噪声污染外,还会对机械传动装置造成严重的损害,影响其使用寿命;另外,还会引发控制系统中的控制量振荡,使得闭环控制的稳定性以及可调整性受到制约。因此,机械振荡的研究以及抑制方法已经成为提高伺服驱动系统性能的一个重要课题。
机械谐振的成因比较复杂,同时受机械系统的固有特性以及负载情况的影响。一般是通过避震的方式避免系统在谐振点工作,或者通过改进机械结构以及加固等被动方式解决此问题。主动方式抑制机械谐振的方法主要包括3种:1)使用传感器直接测量电机端和负载端的位置和速度信号,根据两端信号估算出机械谐振的状态,并进行抑制[1-2]。但这需要额外测量负载侧位置,增加系统成本和复杂性,常规应用无法实现。2)使用传感器测量电机端的位置以及速度信号,并用观测器估计负载转速等变量,进行谐振抑制[3-6]。此方法控制结构复杂,根据不同系统需要设计相应的观测器。3)基于常用的伺服控制系统的控制结构,仅使用一个传感器测量电机端的位置以及速度信号,在控制环路中加入陷波滤波器,或者相位补偿器装置进行补偿,对机械谐振形成抑制[7-11]。
本文主要研究由传动轴系、联轴节等弹性设备以及负载转动惯量引起的机械系统自激振动,建立数学模型进行分析。并针对第三种抑制形式——使用陷波滤波器分析系统性能,理论分析和仿真实验验证了使用陷波滤波器抑制机械谐振的有效性和局限性。
1 机械谐振的原理与影响
1.1 机械谐振产生原理
在实际工业应用中,数控加工设备的机械结构如图1所示。其中电机通过伺服驱动器进行闭环控制,执行机构通过联轴器、传动轴、滚轴丝杠等传动机构与电机联接。
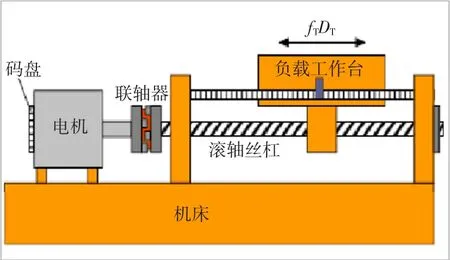
图1 数控加工设备机械结构图Fig.1 Mechanical structure of NC machine
在实际的系统中,传动装置的刚度有限,具有一定弹性。弹性的存在将在系统中引入谐振点,引发机械谐振。不同的机构弹性不同,引发的谐振频率也不同。通常传动装置引起的机械谐振频率集中在100 ~ 2 000 Hz范围内[6],如图2所示。
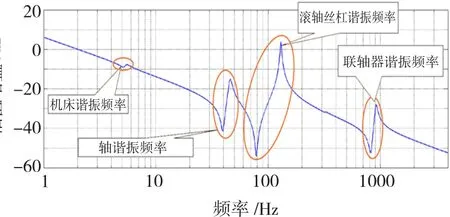
图2 不同因素引起的机械谐振Fig.2 Mechanical resonance caused by different factors
电机、传动机构、执行机构组成的典型双惯量机械传动系统如图3所示。电机和执行机构通过传动轴系联接,传动轴系具有一定的抗扭刚度K和阻尼系数Cw。当传动轴系发生扭转形变时轴系将产生转矩Tw,此转矩对于电机来说可看作是电机的负载转矩,而对于执行机构来说可看作是驱动转矩。伺服驱动器控制电机运行,为电机的转轴提供电磁转矩Te。在电机端电磁转矩Te和传动轴系转矩Tw作用于转动惯量为J1、阻尼系数为C1的电机转轴。在执行机构端,执行机构具有大小为J2的等效转动惯量以及阻尼系数C2,传动轴系转矩Tw与负载转矩Tl共同作用于执行机构最终决定了负载转速。根据以上分析可建立微分方程组为
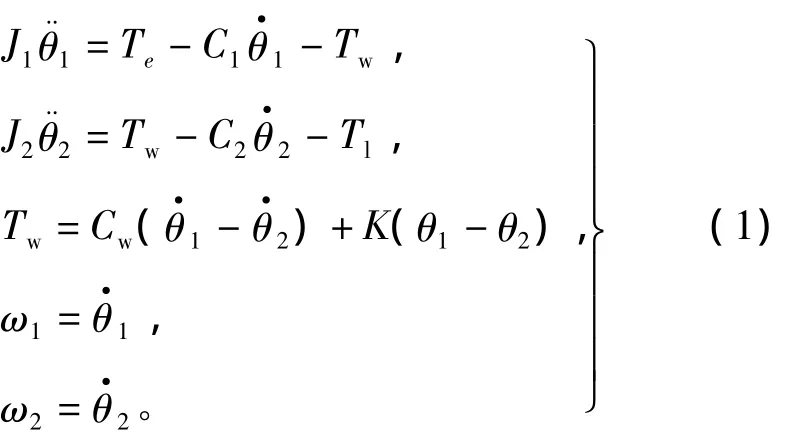
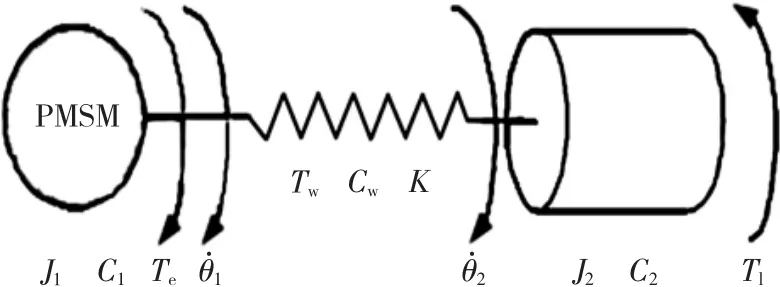
图3 典型双惯量机械传动装置模型Fig.3 Model of typical 2-mass transmission mechanisms
系统中的阻尼系数很小,可忽略阻尼系数从而对系统模型进行化简。对化简后的系统微分方程组进行拉普拉斯变换,得
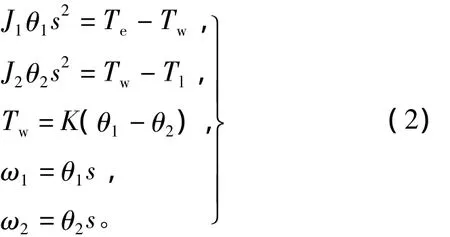
根据式(2)可推导出图4所示的机械传动装置模型框图,进而推导出电机转速、负载转速以及电机电磁转矩之间的传递函数,如式(3)、式(4)、式(5)所示。
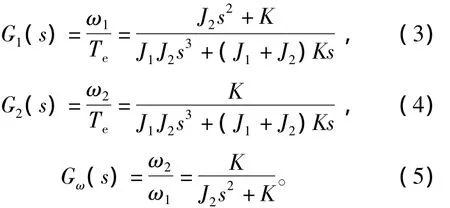
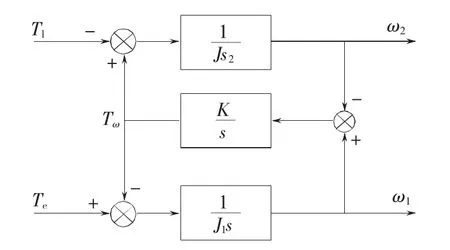
图4 传动装置模型框图Fig.4 Block diagram of transmission mechanisms
图5为实际包含弹性传动装置的转速-电流双闭环控制系统框图。外环转速环,对电机转速ω1进行闭环控制;转速调节器ASR为PI调节器,调节器输出为电流指令值。内环电流环调节器ACR为PI调节器;本文着重研究速度环性能,因此可将电流环的控制对象,即电能变换电路与电机化简成增益为Kc,时间常数为τ的一阶惯性环节。结合式(3)和式(5)的机械系统传递函数,即可得出实际系统模型。
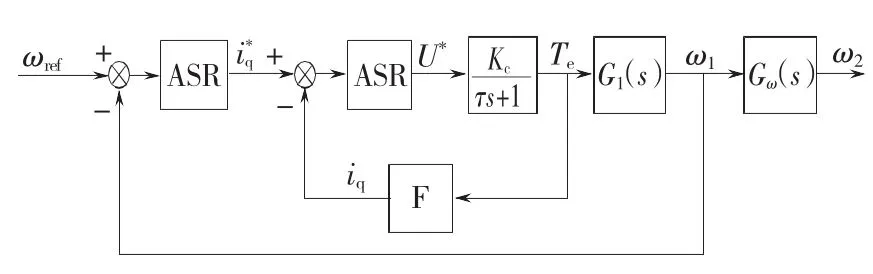
图5 实际系统模型框图Fig.5 Block diagram of actual system
1.2 机械谐振对系统性能的影响
根据以上分析,可以画出包含机械谐振的实际系统波特图,如图6所示。图中曲线A为闭环系统电机转速响应的幅频特性曲线,即ω1/ωref传递函数的幅频特性曲线。由于弹性传动装置的存在,闭环系统电机转速在谐振频率点处出现幅值增益突降。曲线B为式(5)的幅频特性曲线,表示电机转速ω1到负载转速ω2的传递关系。可以看出,传递函数中有一对频率与谐振频率相同的共轭极点,幅值增益突然增大。曲线C为曲线A和曲线B的叠加,为闭环系统负载转速响应的幅频特性曲线,即ω2/ωref传递函数的幅频特性曲线。可以看出闭环系统中存在一个谐振点,系统对于此频率点的响应比较强烈,存在机械谐振。
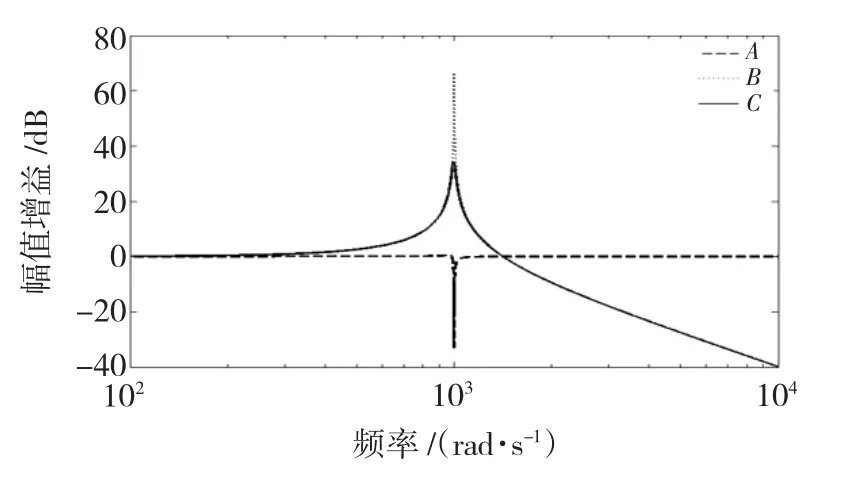
图6 实际系统模型波特图Fig.6 Bode diagram of actual system
图7所示为系统阶跃响应的仿真结果。图7(a)为电机转速阶跃响应曲线,图7(b)为负载转速阶跃响应曲线,图7(c)为电机电磁转矩阶跃响应曲线。
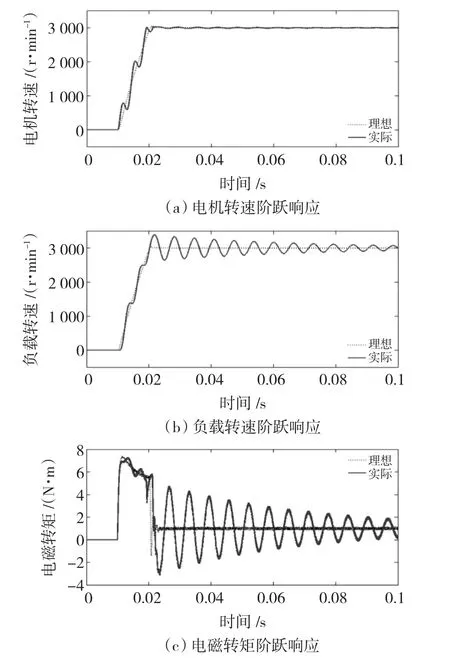
图7 机械谐振仿真结果Fig.7 Simulated performance of mechanical resonance
从仿真结果可看出,跟理想刚性传动装置相比,实际传动装置中电机转速受闭环控制基本稳定,但负载转速以及电机电磁转矩都出现严重振荡。
如图8(a)和图8(b)所示分别为传动轴系中的转速振荡与转角振荡,即传动轴系中的扭转振荡。扭转振荡的存在会损害机械传动装置,降低使用寿命。
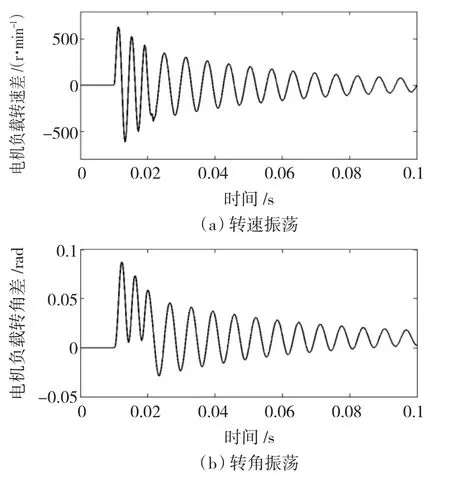
图8 扭转振荡的仿真结果Fig.8 Simulated performance of torsional oscillation
系统中的机械谐振频率和振幅主要受到负载转动惯量J2和传动轴扭转弹性系数K两个参数影响。图9(a)为保持扭转弹性系数K不变,增大负载转动惯量J2对机械谐振现象造成的影响;图9(b)为保持负载转动惯量J2不变,增大扭转弹性系数K对机械谐振现象造成的影响。参数变化情况如表1所示。
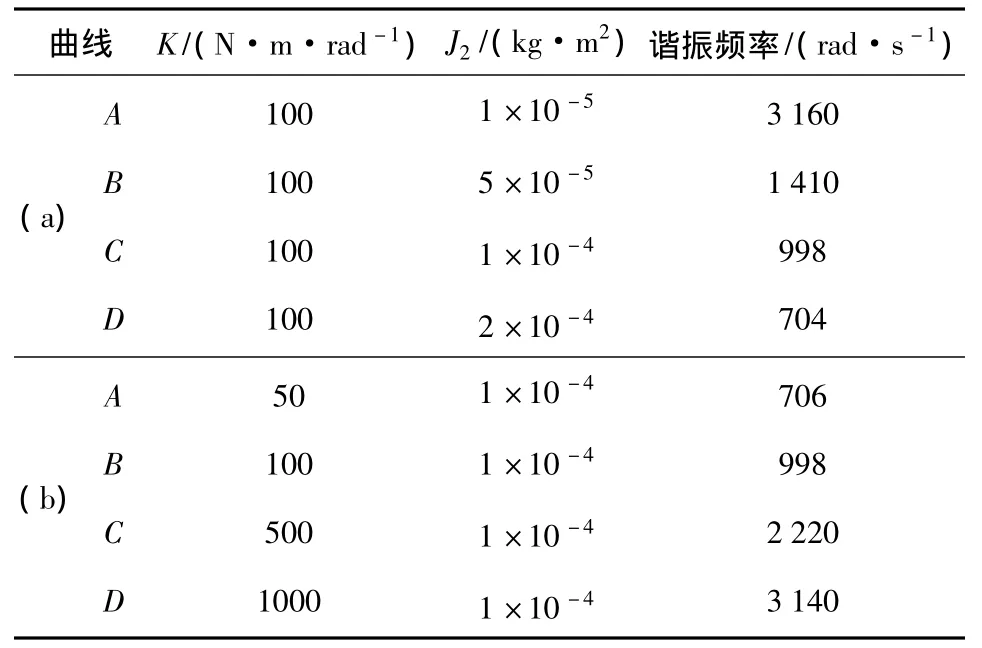
表1 关键参数与谐振现象的关系Table 1 Relationship between key parameters and resonance phenomena
可以看到,如果增大负载转动惯量J2,则会导致机械谐振的频率降低,同时机械谐振的振动幅度也会降低;如果增大传动轴扭转弹性系数K,则会导致机械谐振频率的增大,同时机械谐振的振动幅度会随之降低。弹性和转动惯量两个参数共同作用,最终决定了机械谐振的频率和振动幅值的大小。
此外,由于伺服驱动系统对电机的转速进行闭环控制,控制器的控制参数会对电机的运行状况产生影响,进而间接对机械情况产生影响。主要体现为对振动的幅值以及振幅衰减速度的影响。但是,单纯通过调节控制器的控制参数无法对机械谐振抑制产生显著效果,必须引入其它补偿措施。
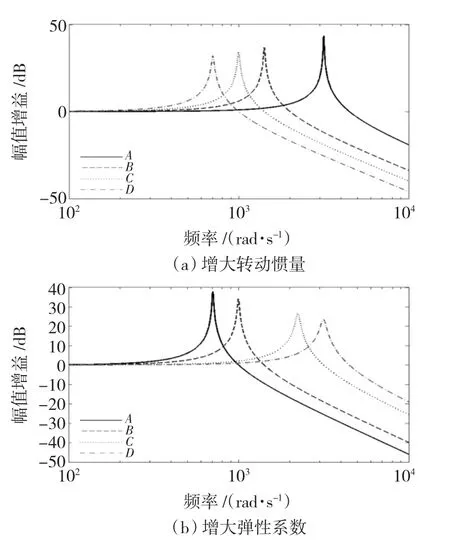
图9 关键参数与谐振现象的关系Fig.9 Relationship between key parameters and resonance phenomena
2 机械谐振的抑制
机械谐振是发生在特定频率点的振动,使用电气方法进行机械谐振抑制,主要是对机械谐振频率点进行补偿,从而抑制谐振现象。本文中主要使用陷波滤波器对机械谐振频率进行补偿,并抑制谐振的产生。
为了能够方便快捷的对陷波滤波器的作用频率,陷波带宽以及陷波深度进行调节,可以选用改进型双T网络陷波滤波器。其传递函数为
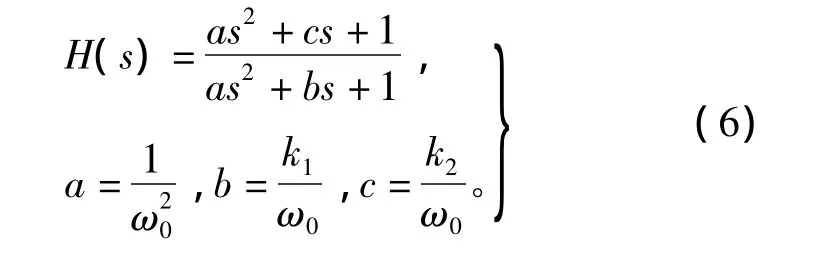
其中,根据滤波器作用的频率点ω0、陷波带宽参数k1以及陷波深度参数k23个变量可决定滤波器的a、b、c3 个系数。
使用陷波滤波器进行机械谐振抑制的系统框图如图10所示。将陷波滤波器串入速度环控制环路中,对转速调节器输出的电流环给定信号进行滤波,抑制电机电流的振荡,进而对电机输出电磁力矩产生抑制,最终达到抑制机械谐振的目的。
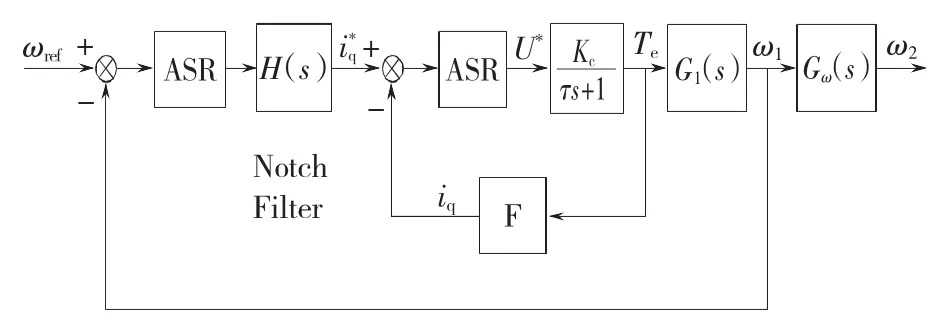
图10 陷波滤波器抑制机械谐振模型框图Fig.10 Block diagram of suppressing mechanical resonance with notch filter
在设计滤波器参数时,应首先确定系统的谐振频率ω0。之后针对谐振频率确定其陷波带宽参数k1和陷波深度k2。
图11中的曲线A、B分别是加入滤波器之前和加入滤波器之后闭环系统负载转速响应的幅频特性曲线。可以看出,加入滤波器后,原系统谐振频率点的幅值增益受到了衰减,因此机械谐振受到了抑制。然而在原系统谐振频率受到抑制的同时,滤波器的加入将在系统中系统引入两个新的谐振点,这两个谐振点频率一个高于原系统的谐振频率,另一个低于原系统的谐振频率。
这两个附加产生的频率点通过调节滤波器参数以及控制系统的PI参数均无法消除。只能通过优化控制器以及滤波器参数削弱谐振现象。
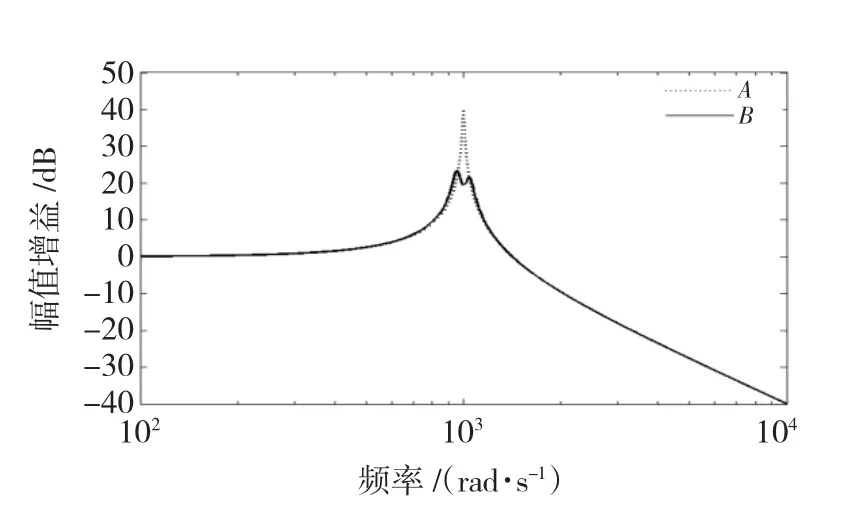
图11 陷波滤波器的作用Fig.11 Function of notch filter
3 仿真和实验
仿真和实验中所使用的永磁同步伺服系统的参数为:电机额定功率0.75 kW;电机额定电流4.4 A;电机额定转矩2.39 N·m;电机额定转速3000 r/min;电机惯量6.72×10-5N·m2;定子电阻 0.45 Ω;定子电感3.9 mH;最大转矩电流13.4 A;传动轴弹性100 N·m/rad;负载惯量 1 ×10-4N·m2。
系统的负载转矩类型为1 N·m摩擦型转矩。系统给定信号为0 r/min→3 000 r/min→0 r/min的正反向阶跃信号。
图12(a)为滤波前后电机转速阶跃响应曲线。可以看出经过滤波后,电机转速中出现了波动。然而在图12(b)所示的滤波前后负载转速阶跃响应曲线中,负载转速振荡受到了明显的抑制。图12(c)中的滤波前后电机输出电磁转矩阶跃响应曲线也表明滤波器抑制了电机交轴电流中的振荡,进而抑制了电机电磁力矩的振荡,最终实现机械谐振的抑制。

图12 机械谐振抑制仿真结果Fig.12 Simulated performance of suppressing mechanical resonance
图13是传动轴系扭转振荡抑制的仿真结果。图13(a)为转速振荡抑制的仿真结果,图13(b)为转角振荡抑制的仿真结果。可以看出,转轴上的扭转振荡受到了极大的抑制。

图13 扭转振荡抑制仿真结果Fig.13 Simulated performance of suppressing torsional oscillation
4 结语
对于包含弹性传动装置的伺服驱动系统,本文分析了机械谐振的产生原理,并对使用陷波滤波器进行机械谐振抑制的方案进行了仿真研究。结果表明,陷波滤波器能够抑制系统中的机械谐振。然而,陷波滤波器在对机械谐振产生抑制的同时,还会在系统中引入两个不同频率的谐振。通过优化控制器以及滤波器参数可以在一定程度上削弱这两个谐振点产生的谐振,但是很难将其完全除去。在设计滤波器时,需要已知谐振的频率。如何能够在线辨识系统的谐振频率、并自动配置滤波器参数将是下一步研究的重点。
[1]HUNG J Y.Control of industrial robots that have transmission elasticity[J].IEEE Transactions on Industrial Electronics,1991,38(6):421-427.
[2]COLOMBI S,RAIMONDI T.Compliance compensation in mechatronic systems[C]//IEEE 20th International Conference on Industrial Electronics,Control and Instrumentation,September 5 - 9,1994,Bologna,Italy.1994,41:946 -951.
[3]OHMAE T,MATSUDA T,KANNO M,et al.A microprocessorbased motor speed regulator using fast-response state observer for reduction of torsional vibrations[J].IEEE Transactions on Industry Applications,1987,IA -23(5):863-871.
[4]SUGIURA K,HORI Y.Vibration suppression in 2-and 3-mass system based on the feedback of imperfect derivative of the estimated torsional torque[J].IEEE Transactions on Industrial Electronics,1996,43(1):56 -64.
[5]VITTEK J,BRIS P,MAKYS P,et al.Control of flexible drive with PMSM employing forced dynamics[C]//2008 13th International Power Electronics and Motion Control Conference,September 1-3,2008,Poznan,Poland.2008:2219-2226.
[6]OHISHI K.Robust position servo system based on vibration suppression control for industrial robotics[C]//The 2010 International Power Electronics Conference,June 21-24,2010,Sapporo,Japan.2010:2230-2237.
[7]VUKOSAVIC S N,STOJIC M R.Suppression of torsional oscillations in a high-performance speed servo drive[J].IEEE Transactions on Industrial Electronics,1998,45(1):108 -117.
[8]FERREIRA J A,DORLAND P,FREDDIE G B.An active inline notch filter for reducing acoustic noise in drives[J].IEEE Transactions on Industrial Electronics,2007,43(3):798 -804.
[9]KUMAGAI S,OHISHI K,MIYAZAKI T.High performance robot motion control based on zero phase error notch filter and D-PD control[C]//IEEE 2009 International Conference on Mechatronics,April 14-17,2009,Malaga,Spain.2009:1-6.
[10]杨辉,范永坤,舒怀亮.抑制机械谐振的一种改进的数字滤波器[J].光电工程,2004,31(S1):30-39.
YANG Hui,FAN Yongkun,SHU Huailiang.An improved digital filter for restraining mechanical resonance frequency[J].Optoelectronic Engineering,2004,31(S1):30-39.
[11]张磊,刘永光,付永领,等.基于自适应陷波器的主动隔振仿真研究[J].系统仿真学报,2005,17(1):234-237.
ZHANG Lei,LIU Yongguang,FU Yongling,et al.Study on simulation of AVI based on adapitive notch filter[J].Journal of System Simulation,2005,17(1):234-237.

