卫星导航接收机基于IIR陷波器的单频干扰抑制性能分析

贺红兵,聂俊伟,徐 博,欧 钢

(国防科技大学电子科学与工程学院卫星导航定位技术工程研究中心,湖南 长沙 410073)

0 引 言

卫星导航接收机中采用的直接序列扩频技术对干扰有一定的抑制作用,然而当干扰强度超出扩频增益所能够提供的抑制能力时,接收机就无法进行正常的捕获跟踪,更无法进行精确的定位、测速以及可靠的通信。因此,必须考虑采取抗干扰措施对干扰进行抑制,以进一步提高接收机的抗干扰能力。

在众多的干扰类型中,单频干扰是一种简单而容易实施的干扰类型。单频干扰抑制技术主要有时域处理、频域处理及空域处理等几种类型。在现有的众多信号处理手段中,时域IIR陷波抑制技术因其实现简单、抗干扰性能好等优点而被广泛使用。目前,国内外针对单频干扰对卫星导航接收机的影响,提出了直接型和格型两种陷波器[1-4].进行了陷波器参数的理论推导，对比分析了各自的性能，并针对二阶陷波器研究了较好的实例应用，然而关于高阶陷波器的研究内容比较少。本文在已有分析的基础上，详细分析了陷波器性能与参数的关系，并重点研究了高阶陷波器的性能。通过高阶陷波器的研究，为下一步后续研究基于高分辨的高阶IIR陷波器的信号分离算法提供了基础。

1 IIR陷波器性能分析

1.1 IIR直接型陷波器性能分析

IIR陷波器按照结构可以分为直接型和格型两种。一个理想的陷波器的频率特性要在消除的信号频率点处,其值等于零;而在其他频率点处,其值等于1.Z平面单位圆附近的零点会在滤波器幅频特性的相应频率处产生陷落,零点离单位圆越近,陷落越深;而Z平面单位圆附近的极点会在滤波器幅频特性的相应频率处产生凸峰,极点离单位圆越近,凸峰越高。由于滤波器稳定性的要求,极点必需配置在单位圆内,显然极点离单位圆越近则极点对零点的抵消作用越明显,得到的滤波器的阻带就越窄,过渡带就越陡峭[5]。

二阶直接型IIR陷波器正是基于以上的陷波机理来进行设计。其传递函数表达式[6]为

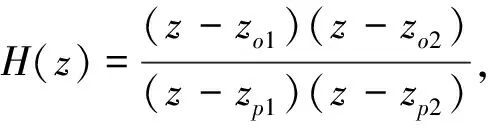
(1)

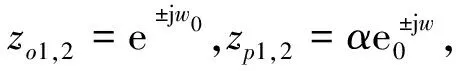
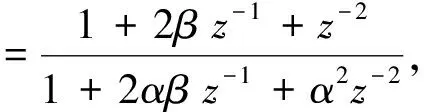
(2)

式中,α为极点结构因子,该陷波器是用单个参数β来限制极点和零点的关系。陷波频率由β来控制。w0表示陷波器的中心频率,其中w0与β的关系为

w0=arccos(-β),

(3)

陷波器中α<1以确保滤波器的稳定。图1示出了选取陷波频率w0=π/5,改变极点结构因子α所得的频率响应曲线。

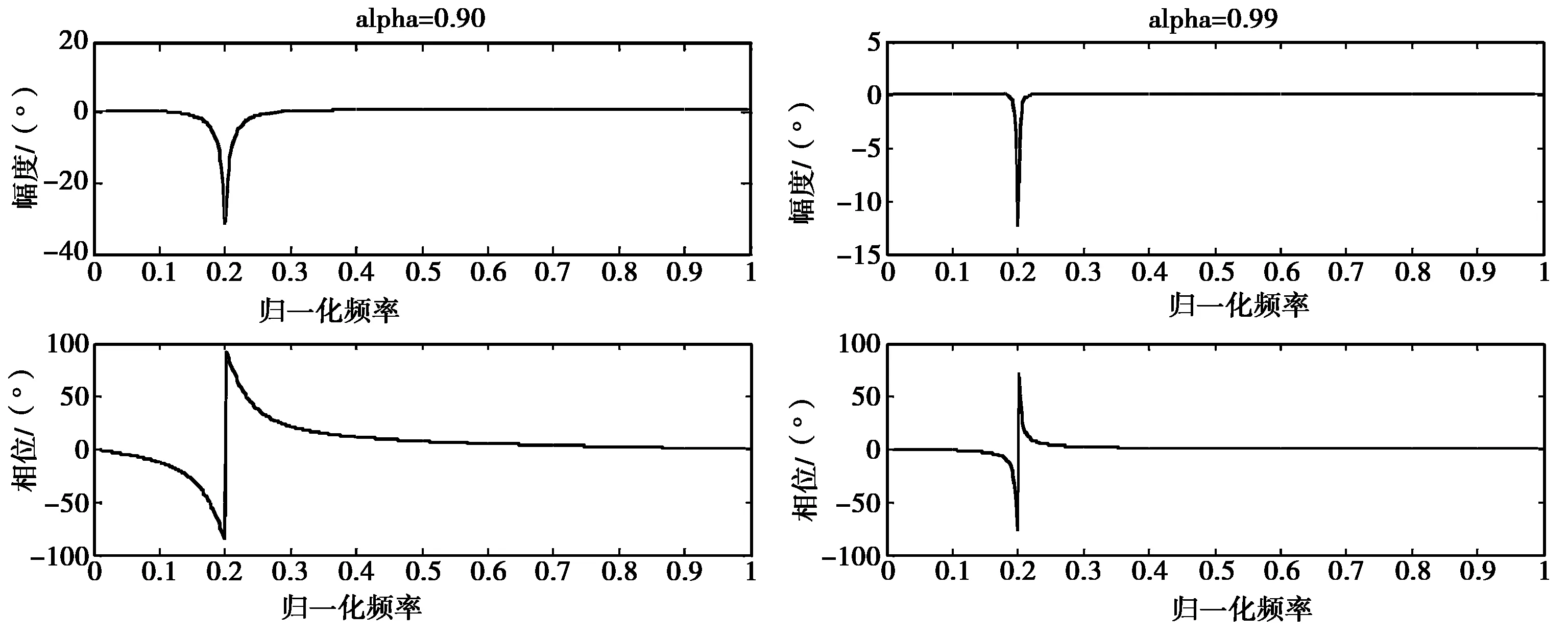
图1 IIR直接型陷波器的频率响应曲线

可以看出,w0决定了陷波器的中心频率。当α较小时,陷波器的带宽较宽,陷波深度较大;当α变大时,陷波器的带宽变窄,陷波深度也变小了。

1.2 IIR格型陷波器性能分析

二阶IIR格型陷波器的传递函数表达式[7-8]为

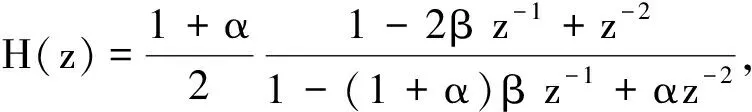
(4)

其中,相关参数设计如下

β=cos(w0),

(5)

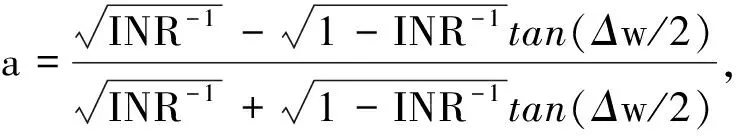
(6)

式中:w0为陷波器的陷波频率; Δw为陷波带宽; INR为干噪比。由式(6)可以看出,参数α是陷波带宽Δw的单调函数。INR一定时,随着α逐渐接近于1,陷波器的带宽逐渐减小,对有用信号的失真也减小。当α=1时,陷波器变成一个直通滤波器。显然,通过调整陷波带宽参数α,可以实现陷波带宽的定量调整,既可以有效抑制单频干扰,又可以降低卫星信号的失真。

1.3 仿真实验验证

设信号为95 Hz和105 Hz的混合正弦信号,干扰为100 Hz的单频信号,采样频率为1 000 Hz,信号中加入高斯白噪声,信噪比为20 dB.分别采用陷波中心频率为100 Hz的二阶IIR直接型和格型陷波器(α均取值为0.98)抑制单频干扰。滤除干扰前后幅频响应如图2所示。

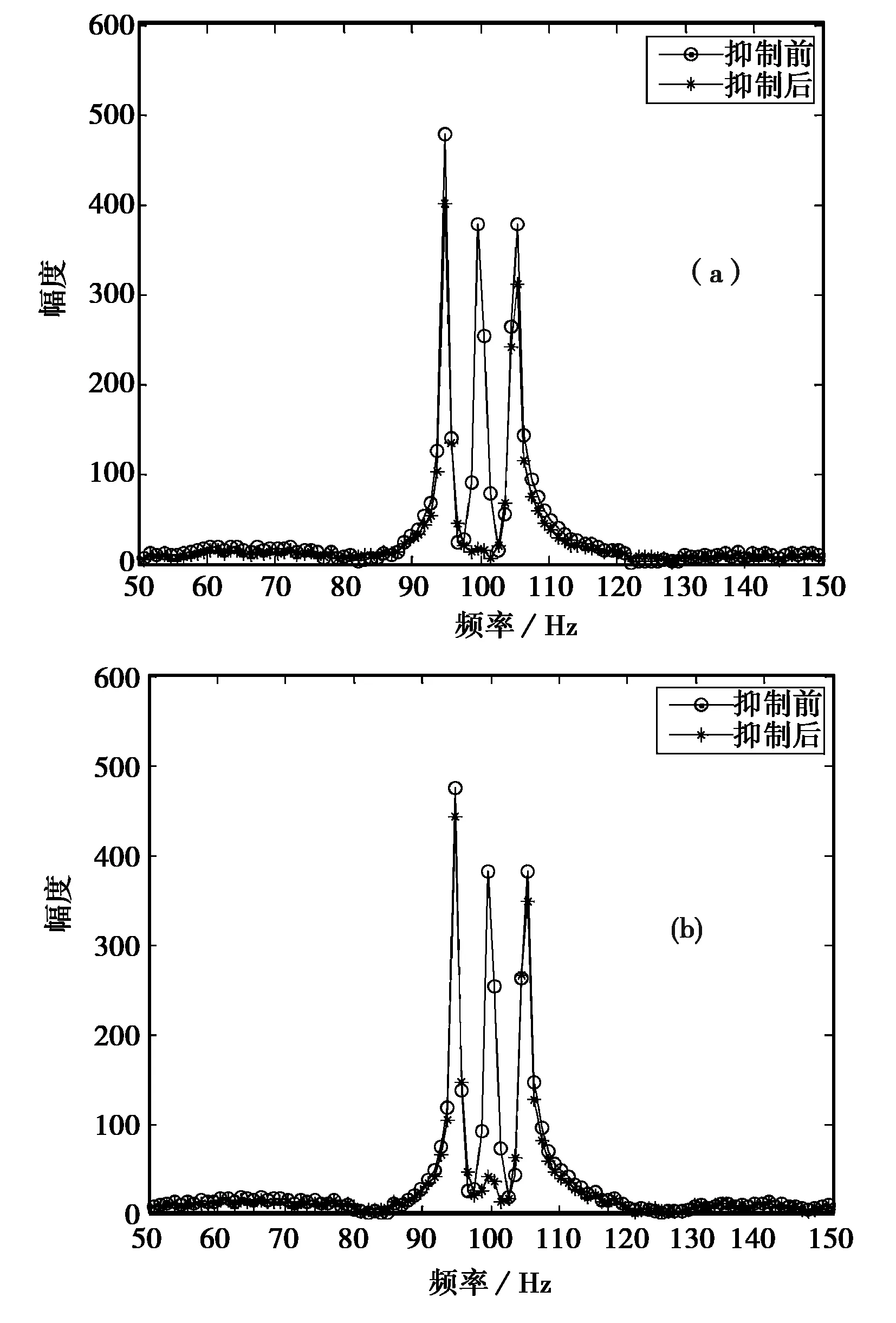
图2 陷波器滤除干扰前后信号幅频图(a)直接型陷波器；(b)格型陷波器

从仿真结果可以看出,不论是直接型还是格型陷波器,都较好地抑制掉100 Hz单频干扰信号,而较完整地保留了原来的95 Hz和105 Hz信号,达到了滤除干扰的预期目的。

2 IIR陷波器性能与参数分析

2.1 陷波器参数α与零陷深度、陷波带宽的关系

为了进一步分析陷波器的性能,以两种陷波器作对比,通过仿真实验数据进行分析。表1和表2示出了两种IIR陷波器在不同α值下的零陷深度、陷波带宽的数据。其中陷波带宽为归一化带宽,陷波频率均为0.02π(10 Hz).

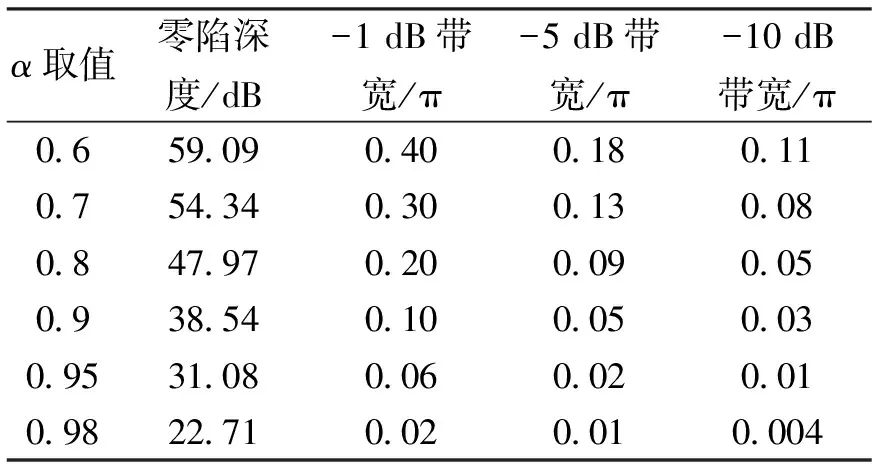
表1 直接型陷波器(陷波频率为0.02π)相关参数关系

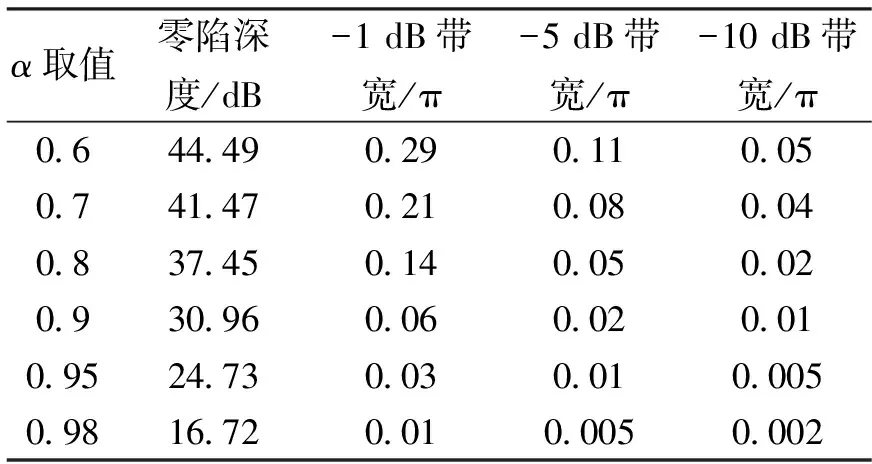
表2 格型陷波器(陷波频率为0.02π)相关参数关系

由表中数据可知,两种陷波器均具有如下性能。即随着α的增大,陷波带宽在不断减小,零陷深度也在不断减小。参数α决定陷波器的陡峭程度。α越小,陷波器的开口越大,对有用信号的失真也就越大。为了使有用信号失真尽量小,就要求参数α必须尽量大。但α越大,同样零陷深度条件下的陷波带宽就越窄,可能就无法有效抑制整个带宽内的干扰。陷波带宽和零陷深度是一组矛盾,因此在选取陷波器带宽参数时,应在一定的带宽下使零陷深度尽可能大,或在满足零陷深度的同时使陷波带宽尽量小。

2.2 陷波器陷波频率与零陷深度、陷波带宽的关系

为了研究上述零陷深度与陷波带宽是否会因陷波频率的位置改变而变化,改变陷波频率(由0.02π变为0.1π,由10 Hz变为50 Hz)重复上述仿真实验,如表3、4所示。

表3接型陷波器(陷波频率为0.1π)相关参数关系

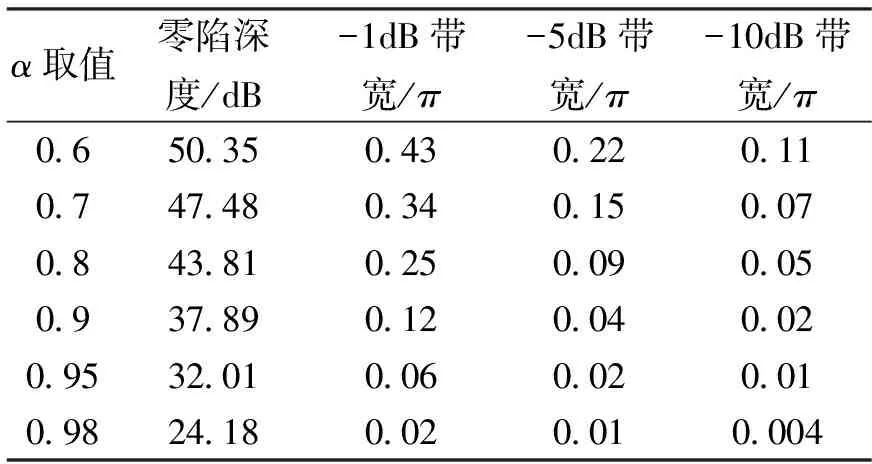
α取值零陷深度/dB-1dB带宽/π-5dB带宽/π-10dB带宽/π 0.650.350.430.220.11 0.747.480.340.150.07 0.843.810.250.090.05 0.937.890.120.040.02 0.9532.010.060.020.01 0.9824.180.020.010.004

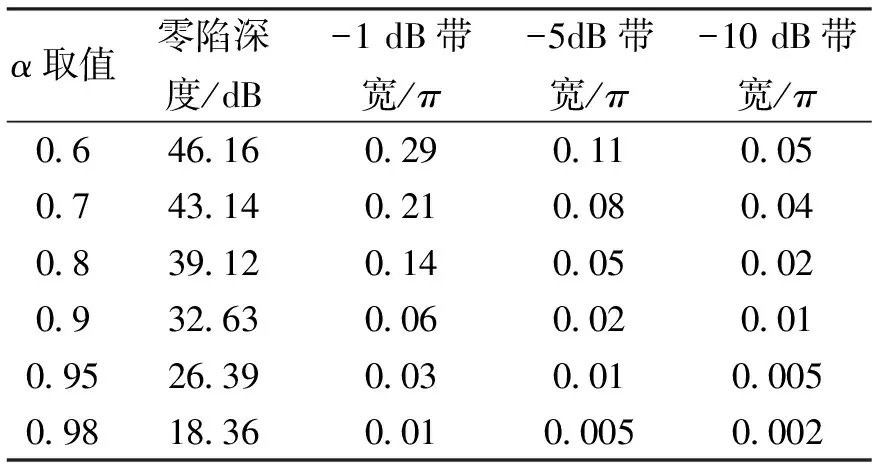
表4 格型陷波器(陷波频率为0.1π)相关参数关系

表3与表1进行对比,表4与表2进行对比,可以看出,对于直接型陷波器来说,在同样α取值的情况下,改变陷波频率,零陷深度和陷波带宽都发生了变化。对于格型陷波器来说,在同样α取值的情况下,改变陷波频率,零陷深度发生了变化,陷波带宽却保持不变。

所以说,相比IIR直接型陷波器,格型IIR陷波器不仅可以准确地控制陷波器的陷波频率,也可以准确地调整陷波器的带宽,成为近年来研究较多且应用较多的干扰抑制方法[9]。

3 高阶IIR陷波器性能研究

3.1 高阶直接型陷波器性能研究

若要设计高阶直接型陷波器时,可以按式(2)把多个陷波器级联起来[10]。如将两个相同参数的二阶直接型陷波器级联,形成四阶陷波器,其传递函数为

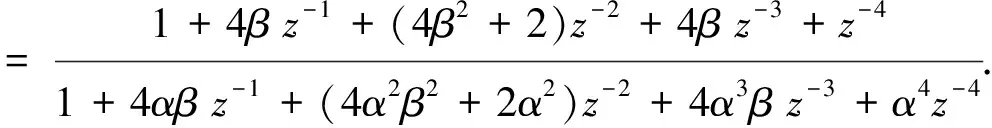
(7)

可以注意到,将多个二阶陷波器进行级联,得到的是偶数阶高阶陷波器。若想得到奇数阶高阶陷波器,则需要一阶陷波器与多个二阶陷波器进行级联。从公式(2)可以看出,二阶直接型IIR陷波器的传递函数可以看成由两个子传递函数乘积构成。即

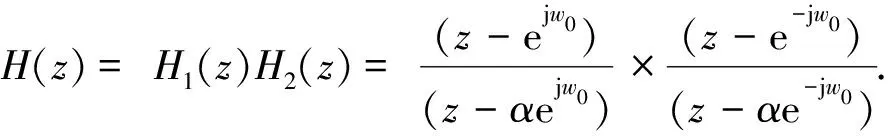
(8)

即H1(z)对应的零极点为zo1和zp1,H2(z)对应的零极点为zo2和zp2.分别画出两个传递函数的频率响应图如图3所示(参数α为0.98,陷波频率为0.2π即100 Hz)。

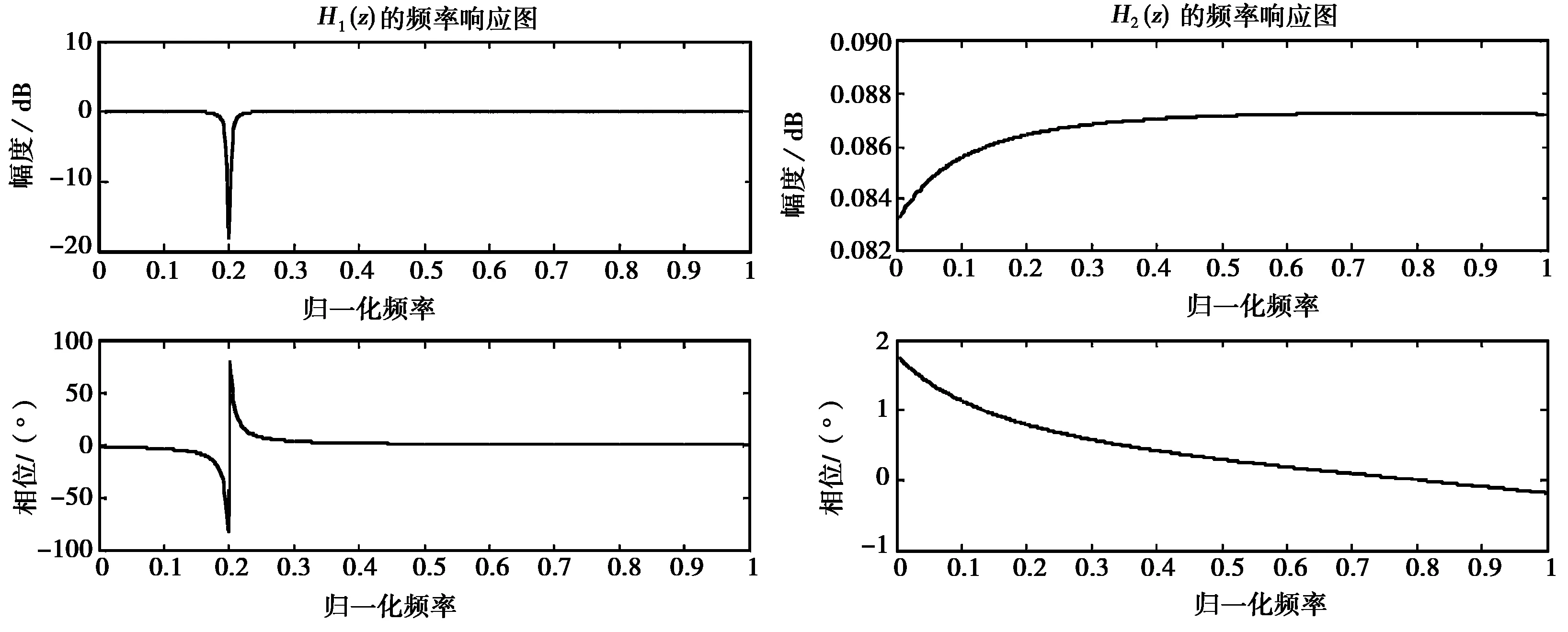
图3 H1(z)和H2(z)的频率响应图

可以看出,H1(z)在0.2π处形成陷波,而H2(z)在整个频带范围内幅度变化较小。事实上,H1(z)即为我们要研究的一阶复数IIR陷波器[11]。由于零极点都只有一个,没有相应的与之共轭的另一对零极点,所以陷波器的系数为复数。所以,一阶陷波器的传递函数为

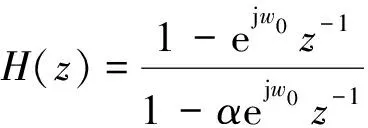
(9)

该陷波器的3 dB带宽由如下公式确定

BW3dB=π(1-α)

(10)

研究了一阶陷波器后,三阶陷波器则可以由一阶陷波器和二阶陷波器级联构成。表5分析比对了各阶陷波器(参数α为0.98,陷波频率为0.2 π即100 Hz)的性能。

从表5中可以看出,一阶陷波器的零陷深度为18.28 dB;二阶陷波器的零陷深度为18.20 dB,比一阶的下降了0.08 dB;三阶陷波器的零陷深度为36.48 dB,正好为两个级联的一阶和二阶陷波器零

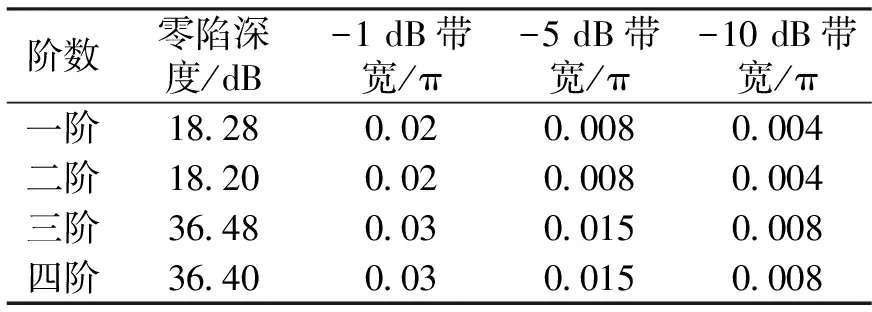
表5 IIR直接型陷波器(不同阶数)相关参数关系

陷深度的叠加;四阶陷波器的零陷深度为36.40 dB,正好为两个级联的二阶陷波器零陷深度的叠加,同时也比三阶的下降了0.08 dB.即零陷深度满足叠加性,然而这种叠加不是无限制的,仿真表明,从九阶陷波器开始这种叠加性便不再满足。另一方面,一阶和二阶陷波器的陷波带宽一样,三阶和四阶陷波器的陷波带宽一样,且四阶陷波器陷波带宽相比较二阶陷波器有所变大。

3.2 高阶格型陷波器性能研究

对于格型陷波器,仿照直接型的研究方法,将两个二阶格型陷波器进行级联得到四阶陷波器,其传递函数为

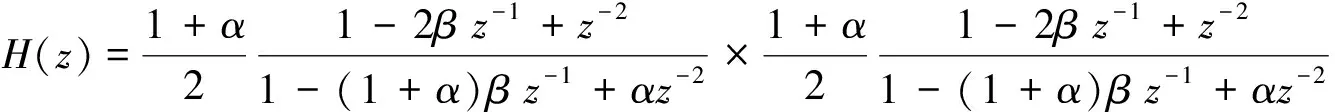
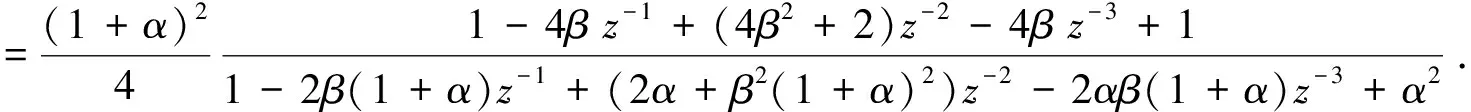
(11)

将二阶和四阶格型陷波器(参数α为0.98,陷波频率为0.2 π即100 Hz)的性能分析比较由表6所示。

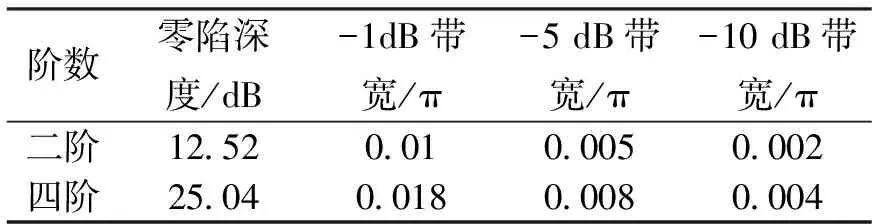
表6 IIR格型陷波器(不同阶数)相关参数关系

从表6中可以看出,二阶陷波器的零陷深度为12.52 dB,四阶陷波器的零陷深度为25.04 dB,正好为两个二阶陷波器零陷深度的叠加,而陷波带宽相比较二阶陷波器有所变大。

3.3 仿真实验验证

同前面的仿真实验条件一样,此时分别采用陷波中心频率为100 Hz的四阶IIR直接型和格型陷波器(α均取值为0.98)来抑制单频干扰。滤除干扰前后幅频响应如图4所示。

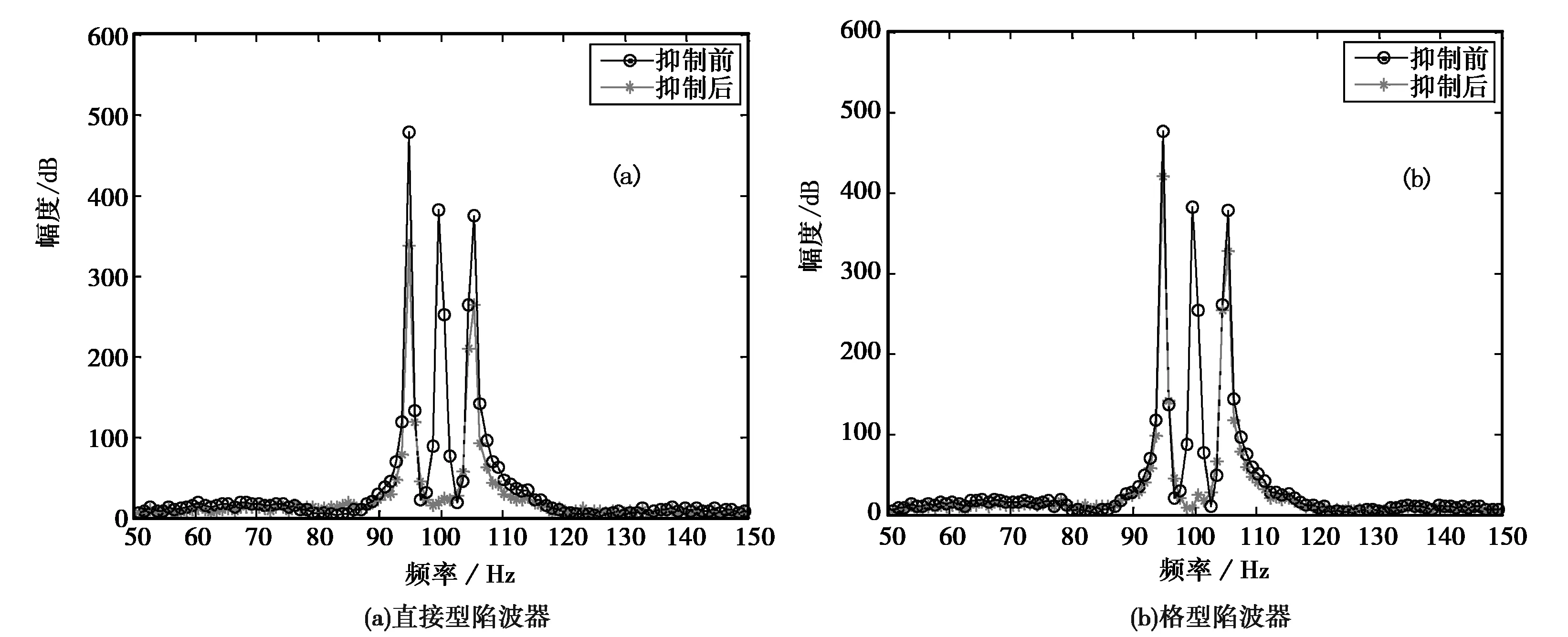
图4 高阶陷波器滤除干扰前后信号幅频图

对比图2与图4可以看出,不论是直接型还是格型,虽然二阶陷波器的零陷深度不如四阶的,但对于100 Hz干扰信号已经进行了较好的抑制,二者对于干扰的抑制效果差不多。相反,由于四阶陷波器的陷波带宽有所变大,对于信号失真而言,四阶反而要比二阶大一些。因此对于单个单频干扰,使用一个二阶IIR陷波器即可达到较好的效果,干扰参数的估计与陷波器的设计也均较为简单。

3.4 高阶陷波器的应用

正如上文指出,对于一个单频干扰,使用一个二阶IIR陷波器去除干扰,是一种非常有效的方法。但是当面临有多个单频干扰或者是窄带干扰时,采用一个二阶IIR陷波器无法达到理想的抗干扰效果,此时考虑采用级联形式的高阶陷波器来解决。

同二阶IIR陷波器一样,该级联陷波器的性能可以通过调整级联阶数、陷波频率的间隔和陷波深度决定,实际中根据抗干扰需求进行选择。在此设计一个高阶陷波器,由5个二阶IIR格型陷波器级联构成[12]。各个陷波器的陷波频率分别为0.26 π、0.28 π、0.30 π、0.32 π、0.34 π(采样速率为1 000 Hz)。考虑到实现的复杂度和资源代价,每个陷波器均取相同的参数α.在这里,分别取α为0.85和0.98,得到两种高阶陷波器的频率响应图如图5所示。

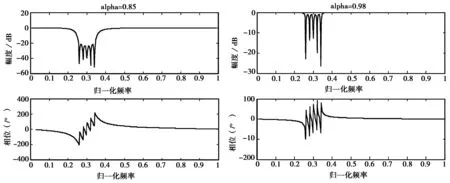
图5 高阶陷波器的频率响应图

可以看出,当α取值为0.85时,级联后的陷波器的陷波频率为0.3 π,陷波带宽为0.1 π,这种高阶陷波器可以用来抑制窄带干扰,陷波效果可以达到20 dB以上。当α取值为0.98时,由于各陷波器的陷波带宽均比较小,级联后的陷波器陷波频率依然分布在不同的陷波位置,这种高阶陷波器可以用来抑制多个单频干扰。在实际应用中,要根据具体的干扰类型,设计不同的参数来满足抗干扰要求。

4 结束语

针对卫星导航接收机中常见的单频干扰展开研究,分析比较了直接型和格型两种陷波器的性能,研究了陷波器参数与零陷深度、陷波带宽的关系,并基于二阶陷波器扩展分析了高阶陷波器的抑制性能,指出了高阶陷波器的应用。通过一系列的仿真实验,说明了IIR陷波器的抑制性能和应用价值。

[1]JUN WON CHOI, NAM IK CHO. Suppression of narrow-band interference in DS-spread spectrum systems using adaptive IIR notch filter[J]. Signal Processing, 2002,82(12):2003-2013.

[2]MVUMA A, Adaptive optimization of notch bandwidth of an IIR filter used to suppress narrow-band interference[C]//In proceeding of IEEE International Symposium on Circuits and Systems, 2002.

[3]MVUMA A, NISHIMURA S, HINAMOTO T. Adaptive optimization of notch bandwidth of an IIR filter used to suppress narrow-band interference in DSSS System[J]. Ieice Transactions on Fundamentals of Electronics, Communications and Computer Sciences, 2002, E85-A (8): 1789-1797.

[4]QIN Peng, CAI Ping. A novel algorithm of adaptive IIR lattice notch filter and performance analysis[J]. Journal of Shanghai University(English Edition), 2007,11(5):485-489.

[5]冯华君,洪淑月,施晓钟.借助Z变换和零极点设计数字陷波器[J].浙江师范大学学报·自然科学版,2004,27(1):26-29.

[6]冯冀宁,吴嗣亮,姜 伟,等.DSSS窄带干扰抑制滤波器性能研究与比较[J].北京理工大学学报,2010,30(6):727-732.

[7]龚文飞,吴嗣亮,李加琪.直扩系统中IIR格型滤波器抑制窄带干扰新方法与性能分析[J].电子与信息学报,2010,32(10):2473-2480.

[8]龚文飞, 孙 昕,吴嗣亮.卫星导航接收机陷波器级联抑制窄带干扰研究[J].宇航学报,2010,31(12):2704-2712.

[9]龚文飞,孙 昕.卫星导航接收机时域窄带干扰抑制滤波器设计与性能分析[J].信号处理,2011,27(11):1774-1780.

[10]李峥嵘,桑怀胜,王飞雪,等.稳健的数字IIR滤波器设计[J].国防科技大学学报,2003,25(4):31-38.

[11]王 勇,田 斌,向 新,等.一种应用于限制零极点位置复数陷波器的迭代算法[J].信号处理,2007,23(1):6-10.

[12]李献斌,王跃科,杨 俊.级联陷波器抗窄带干扰设计与实现[J].电子测量与仪器学报,2013,27(6):493-499.